Delta机器人增广非线性PD控制研究
2021-12-29王钰奉陈伟堤施祥玲于文凯
王钰奉,陈伟堤,施祥玲,祁 佩,于文凯
(1.上海航天设备制造总厂有限公司,上海 200245;2.上海宇航系统工程研究所,上海 200245)
0 引言
Delta机器人具有刚度高、负载自重比小、动力性能好等优点,适用于高速分拣领域。其应用对保证产品质量,提高劳动生产率,降低生产成本具有重要的意义。目前,国内工业界和学术界均对其展开了研究,取得了一定的成果,但国产化的Delta机器人性能还有待提升,在综合设计与优化、控制方法上所做的工作还远远不足[1-3]。其中,控制策略是保证机器人系统高效、稳定运行的关键,其优劣对机器人的工作状态有着重要的影响。当前,高效高精度的控制方法仍是Delta机器人研究领域的重要方向。
机器人控制策略可分为非基于动力学模型的控制和基于动力学模型的控制。前者不考虑机器人的动力学特性,将其当成多个单输入单输出系统,控制结构简单、运算量小、易于实现,在机器人前期的样机研究中应用广泛。Nabat V等[4]将PI控制策略用于Par4并联机器人初期的样机开发。Choi H B等[5]在H4机器人样机设计中使用了PD控制和速度前馈PD控制。基于动力学模型的控制方法以机器人的逆动力学模型为基础,根据逆动力学关系得到机器人沿期望轨迹运动时所需的驱动力或力矩,来达到跟随期望轨迹的目的,主要有计算力矩(CT)控制和增广PD(APD)控制。其中,增广PD控制采用力矩前馈补偿结合位移和速度反馈消除偏差,其驱动力矩可以在离线状态下得到,在线运算量小,伺服控制率高。Choi H B等[5]采用增广PD对H4并联机器人进行控制,其轨迹跟踪精度优于PD控制和速度前馈PD控制。
对多数机器人系统,增广PD控制能获得很好的控制效果,但依赖于精确的动力学模型,而实际机器人系统的模型误差、摩擦力、外界扰动等非线性因素不可避免,实际模型很难完备建立。针对此问题,有两种改进思路:其一,结合先进的控制理论和方法如:滑模变结构控制[6]、神经网络控制[7-8]、H∞鲁棒控制[9]等对机器人进行控制,但该方法要求系统硬件开放程度高,且控制结构复杂、运算量大,实际工程中应用较少;另一种方法是通过非线性经验函数实现控制参数的自动调整,该方法保留了增广PD控制结构简单、参数物理意义明显的特点,且能有效地提高控制精度和抗干扰能力[10-13]。文献[10-11]将一类非线性经验函数引入到并联机器人的控制中,设计了增广非线性PD(ANPD)控制器,其控制精度和抗干扰能力优于线性增广PD控制。文献[12-13]提出一类非线性饱和函数,采用增广非线性PD控制策略对机器人进行控制,能获得更快的响应速度和更高的控制精度。
本文首先对Delta机器人进行动力学建模;在此基础上,立足于工程化应用,采用增广非线性PD控制策略对自研的Delta机器人进行控制;最后,在联合仿真虚拟样机和自研的机器人实物样机上对增广PD控制和增广非线性PD控制的控制效果进行分析和比较。
1 Delta机器人动力学建模
考虑Delta机器人从动臂为轻质铝合金材料,采用集中质量代替连续质量对从动臂进行简化,如图1所示,将从动臂质量1/3分解到动平台,其余2/3分解到主动臂末端,以提高动力学模型的求解效率。
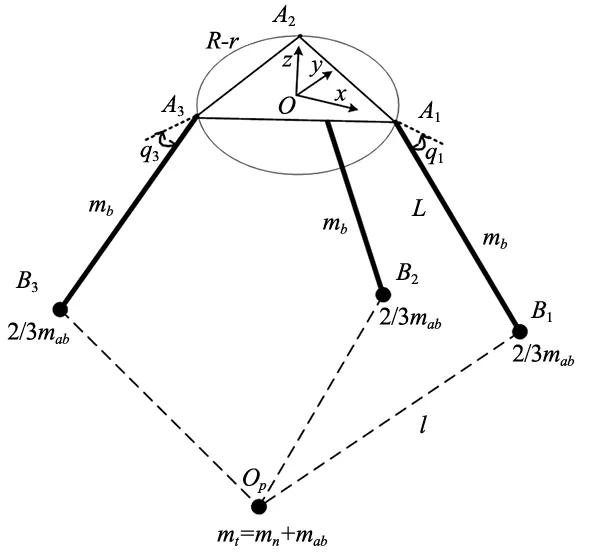
图1 Delta机器人质量分布
在此基础上,基于虚功原理对Delta机器人系统进行动力学建模,最终得到:
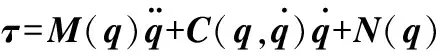
(1)
式中,τ为关节驱动力矩,τ=[τ1τ2τ3]T;M(q)为等效质量矩阵,M(q)=Ibt+mntJTJ;Ibt为主动臂惯量。
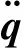
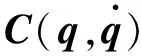
mnt为动平台等效质量,mnt=mn+mab;mn为动平台质量;N(q)为重力项,N(q) =Gnt+Gbg;
Gnt=mnt[0 0g]T;
2 Delta机器人增广非线性PD控制策略
采用非线性函数代替增广PD控制中的定常控制参数,使其能够根据反馈偏差自适应调整控制参数,实现对Delta机器人的增广非线性PD控制。
2.1 增广PD控制策略
增广PD控制由PD控制加期望状态进行逆动力学计算得到的驱动力矩前馈补偿组成。其中,PD控制的控制率为:
(2)
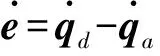
PD控制对机器人3个关节进行独立控制,并未考虑关节间的耦合关系。在PD控制的基础上加入期望状态的力矩前馈项得到增广PD控制。对Delta机器人设计增广PD控制的控制率为:
(3)
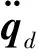
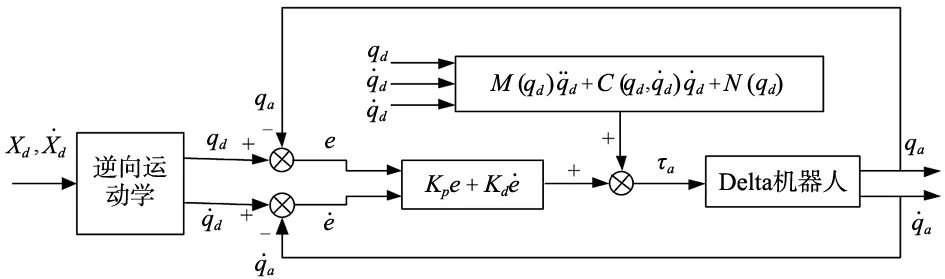
图2 Delta机器人增广PD控制系统原理图
2.2 增广非线性PD控制
为实现非线性PD控制,引入一类近似势能函数:
(4)
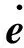
(5)
式中,sign(·)为标准符号函数,α,β,δ∈(0,∞)且β>δ为设计参数,根据控制器反馈偏差确定数值大小。
对于Delta机器人系统,利用式(5)的非线性饱和函数代替传统PD控制的定常控制参数,同时结合线性增广PD控制器的设计方法,设计Delta机器人增广非线性PD控制的控制率为:
(6)
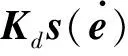
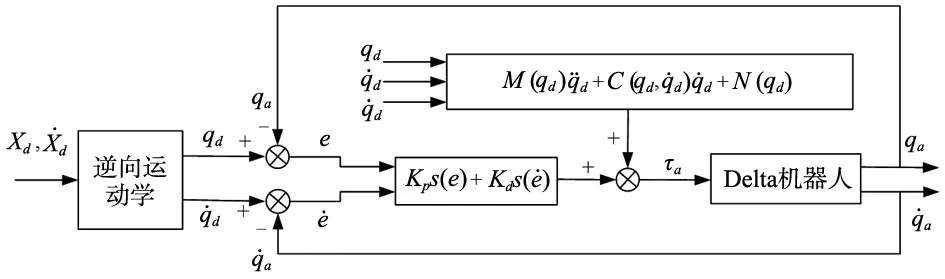
图3 Delta机器人增广非线性PD控制系统原理图
3 联合仿真分析
结合ADAMS软件中的动力学原理样机和Simulink软件中的控制模块,以模型转换的方式建立机器人运动控制联合仿真虚拟样机。分别采用增广PD和增广非线性PD控制策略对机器人样机进行控制,分析和比较两种控制算法的控制效果。
联合仿真技术路线如图4所示,Simulink控制模块包含轨迹生成、运动学转换、动力学补偿、电机控制、控制策略等,其输入为机器人关节位移、速度、加速度等反馈状态量,输出为关节力矩等控制量。ADAMS动力学原理样机包含机器人本体、工作环境约束、构件属性、运动约束、驱动装置等,其输入为控制量,输出为反馈状态量。两者通过TCP/IP调用实现数据通讯。
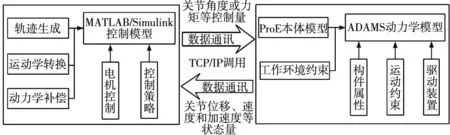
图4 联合仿真技术路线
最终建立联合仿真平台如图5所示。电机控制模块中伺服电机采用力矩控制模式;力矩前馈模块从MATLAB软件的存储空间读取动力学计算结果进行力矩前馈补偿;角度和角速度偏差反馈模块对工作空间读取的期望关节角度和角速度与样机输出的实际关节角度和角速度偏差进行反馈。
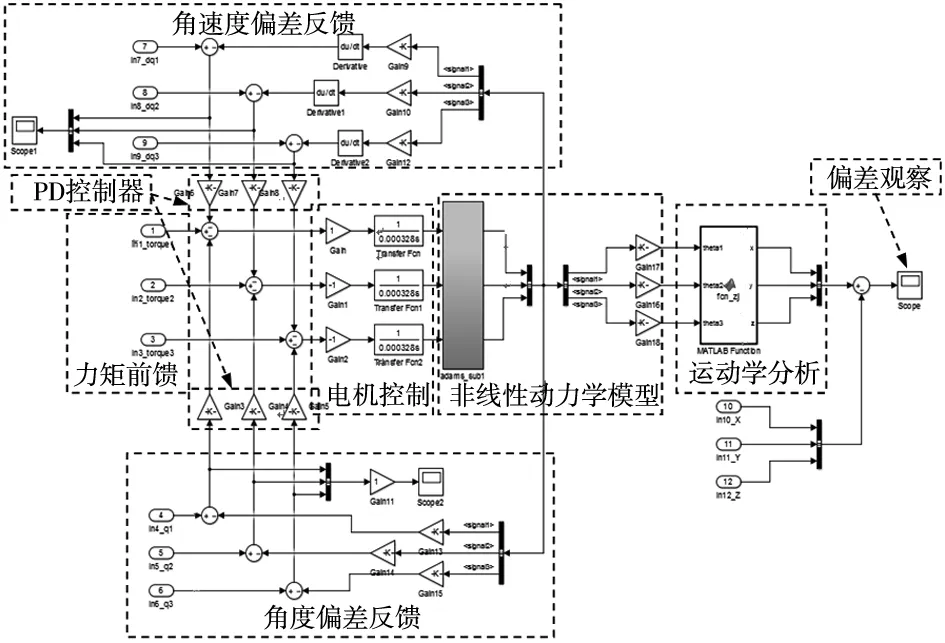
图5 联合仿真分析平台
仿真时机器人末端运动为门型轨迹(adept motion),以位置坐标(90,110,-180)和(-80,-70,-180)为目标点,设定单程高速运动周期T=0.2 s,低速运动周期T=0.5 s,轨迹规划方法参考文献[14]。
采用增广PD控制策略对机器人进行控制,仿真过程中整定控制参数为:Kp1=Kp2=Kp3=0.95,Kd1=Kd2=Kd3=0.012,得到机器人末端轨迹跟踪误差如图6所示。由图可知:运动周期T=0.5 s时,轨迹误差在t=1.32 s到达最大值为E=1.745 mm;运动周期T=0.2 s时,轨迹误差在t=0.64 s取最大值为E=2.852 mm。

(a) 运动周期T=0.5 s轨迹误差曲线
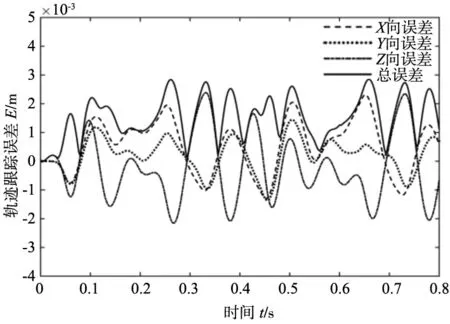
(b) 运动周期T=0.2 s轨迹误差曲线图6 增广PD控制轨迹跟踪误差
采用增广非线性PD控制策略对机器人进行控制,仿真过程中整定控制参数为Kp1=Kp2=Kp3=0.95,Kd1=Kd2=Kd3=0.012,αp1=αp2=αp3=0.55,δp1=δp2=δp3=0.05,βp1=βp2=βp3=1.0,αd1=αd2=αd3=0.05,δd1=δd2=δd3=0.01,βd1=βd2=βd3=1.32。轨迹跟踪误差如图7所示。由图可知:运动周期T=0.5 s时,轨迹误差在t=1.63 s到达最大值为E=1.749 mm;运动周期T=0.2 s时,轨迹误差在t=0.08 s取最大值为E=1.895 mm。跟线性增广PD控制相比,其控制精度提高,特别是高速运动时提升更为明显。
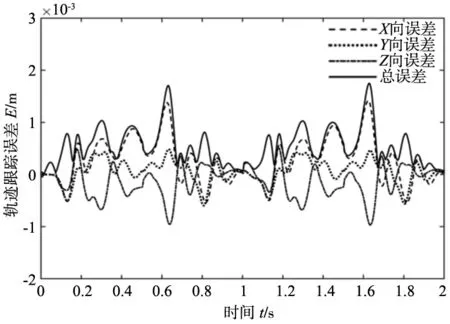
(a) 运动周期T=0.5 s轨迹误差曲线
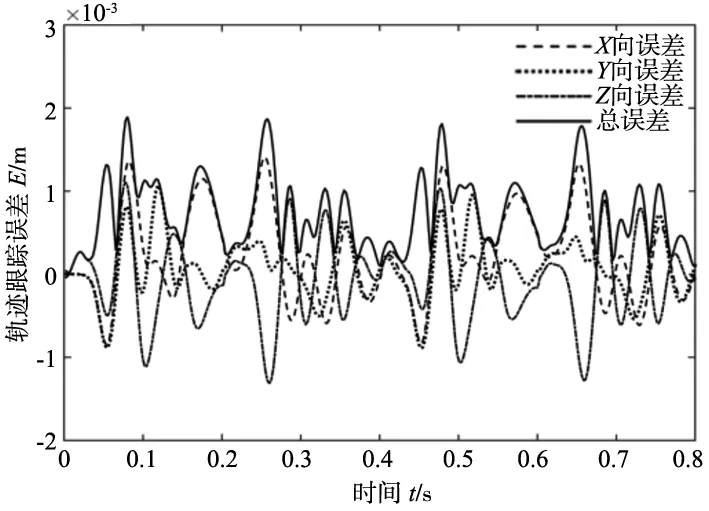
(b) 运动周期T=0.2 s轨迹误差曲线图7 增广非线性PD控制轨迹跟踪误差
4 运动控制试验
为了验证控制策略对实际机器人系统的控制效果,通过自研机器人样机与激光跟踪仪搭建运动控制试验平台,在平台上开展重复定位试验。试验平台主要包括:Delta机器人样机,激光跟踪仪、靶镜支撑架、Delta机器人人机界面、激光跟踪仪上位机等,如图8所示。

图8 运动控制试验平台
设置试验条件为:①在两种运动速度下开展控制试验;②设置轨迹起点坐标为(90,110,-180),终点坐标为(-80,-70,-180);③机器人末端在两个目标点之间往返运动10次,停止在终点(-80,-70,-180)处用激光跟踪仪测量末端的位置误差。
采用增广PD和增广非线性PD控制策略对机器人进行控制,试验中对控制参数进行微调整,最终得到两种控制算法的末端定位误差分别如图9、图10所示。
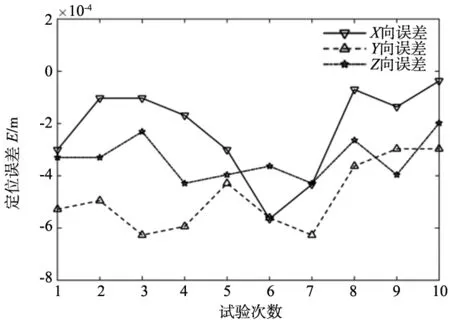
(a) 运动周期T=0.5 s末端定位误差
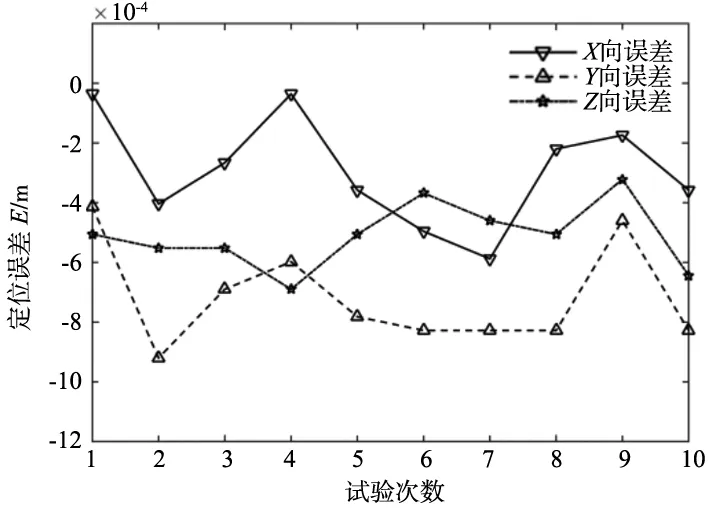
(b) 运动周期T=0.2 s末端定位误差图9 增广PD控制重复定位误差
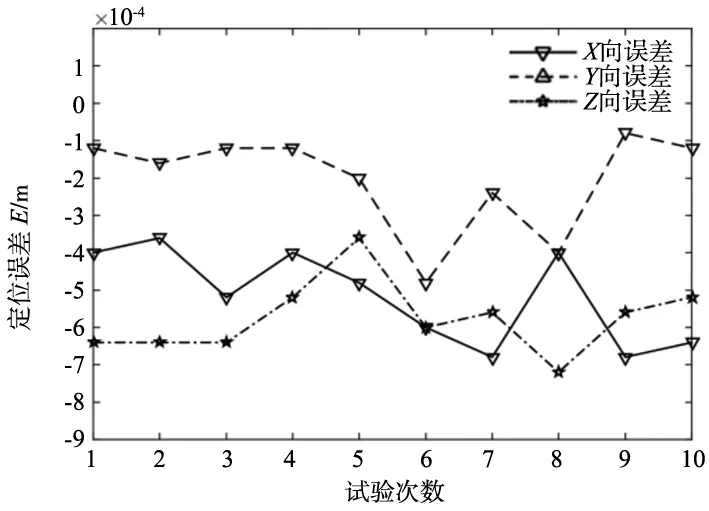
(a) 运动周期T=0.5 s末端定位误差
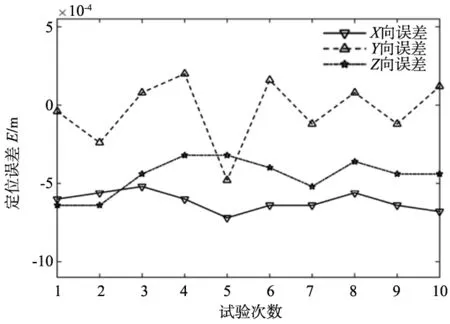
(b) 运动周期T=0.2 s末端定位误差图10 增广非线性PD控制重复定位误差
采用“3σ法则”进行分散度统计,得到机器人末端重复定位精度如表1所示。

表1 末端重复定位精度
分析表中的数据可得到以下结论:无论低速还是高速运动,增广非线性PD控制的控制精度优于传统线性增广PD控制。
5 结论
(1) 基于虚功原理建立Delta机器人动力学模型,采用集中质量代替连续质量对从动臂进行简化,有效地提高了动力学模型的求解效率。
(2) 引入非线性饱和函数代替定常控制参数,实现对Delta机器人的增广非线性PD控制。为了对控制算法的控制效果进行分析和比较,结合ADAMS与Simulink软件建立了联合仿真虚拟样机,同时在自研的实物样机上搭建了运动控制试验平台。
(3) 仿真和试验结果表明:跟增广PD控制相比,采用增广非线性PD控制策略对Delta机器人进行控制能获得更高的控制精度,在高速时精度改善更为明显。
