基于传动误差的齿轮系统时变频响函数辨识*

朱子文，贾山虎，何声馨，张二亮

(郑州大学机械与动力工程学院，郑州 450001)

0 引言

现代机械传动系统中，齿轮是最重要的部件之一，由于其恒定的传动比、大功率及高效率等特点，在生产制造中被广泛使用。齿轮传动系统是一种复杂的弹性结构系统，其动态特性研究一直备受关注[1]。然而，齿轮箱的动力学建模是机械工程领域公认的极具挑战性的课题之一。从系统辨识理论的角度，开展齿轮系统动态特性的建模研究具有重要的意义。

齿轮箱动态特性或其参数辨识得到了国内外学者的广泛关注。Wang J G等[2]针对单级齿轮箱模型存在的非线性动态特性，提出了一种单级齿轮箱的伪线性神经网络辨识方法。Sawalhi N等[3]通过对齿轮箱振动加速度信号的测量，辨识了齿轮的齿数及其转速。Ankur S等[4]基于模态分析理论，研究了健康齿轮和裂纹齿轮的啮合刚度对齿轮转子系统固有频率、模态振型和频响函数的影响。Rune P等[5]应用时变模态分析方法对具有周期性时变啮合刚度的齿轮系统进行理论分析，得到了齿轮的基频和参数共振频率随转速的变化规律。Ericson T M等[6]运用经典实验模态分析技术对行星齿轮的动态特性进行了表征，得到了行星齿轮的固有频率、振型和频响函数。综上所述，齿轮传动过程中表现出典型的(周期)时变特性尚没有得到系统建模和研究。

齿轮(动态)传动误差是表征齿轮系统动态特性的主要指标之一。众多学者在传动误差的仿真计算与实验测量方面做了大量的工作。汪中厚等[7]基于有限元理论和瑞利阻尼数学模型，在不同阻尼条件下，对螺旋锥齿轮的动态传动误差进行了仿真。袁勇超等[8]基于光栅测量方法，建立了传动误差测试平台以及数据采集系统，提高了齿轮动态传动误差检测精度。李福洋等[9]通过非接触式光学测量方法，对齿轮副的传动误差进行了高精度的测量。另外，传动误差与加工制造误差之间的关系也得到了深入研究[10-11]。

本文以齿轮箱传递的扭矩为输入，视动态传动误差为齿轮系统响应，采用系统与控制领域中周期时变辨识理论，建立了齿轮系统的时变频响函数辨识方法。进一步通过齿轮系统时变动力学数值模型，验证了该方法的有效性。本文为齿轮系统动态研究提出数据驱动建模新方法，这可为齿轮系统的减振降噪、故障诊断及智能控制提供基础。

1 齿轮时变动力学模型

1.1 三自由度齿轮集中质量模型

齿轮系统是一种参数激励和非线性并存的弹性结构系统，如果齿轮传递较大的载荷，齿轮的啮合表面始终处在接触状态，轮齿间的齿侧间隙不会对系统的动态特性产生影响[12]。本文忽略齿轮侧隙，运用集中质量法建立了经典的三自由度齿轮集中质量模型，该模型在重载工况条件下较符合工程实际，如图1所示。

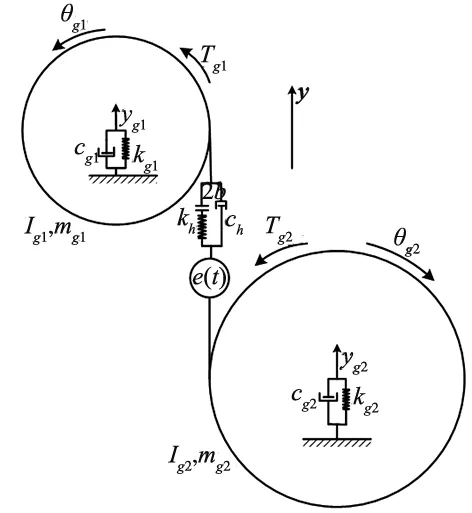
图1 齿轮转子系统动力学模型

由牛顿定律可推导出图1所示三自由度齿轮系统的动力学微分方程：

(1)

式中，ygi和θgi分别为第i个齿轮(i=1,2)的平动位移以及扭转振动位移，Ig1和Ig2为齿轮转动惯量，mg1和mg2为齿轮平移质量，dg1和dg2为基圆直径，cb1、cb2和ch(t)分别为主、从动轮的支撑阻尼和轮齿啮合阻尼，kb1、kb2和kh(t)分别为主、从动轮的支撑刚度和轮齿时变啮合刚度。

(2)

(3)

式中，mc1为齿轮副等效质量。

Fm=2Tg1m/dg1=2Tg2m/dg2

(4)

FaT(t)=mc1Tg1a(t)/2Ig1

(5)

式中，Fm为由扭矩的平均分量(Tg1m)引起的轮齿啮合力，FaT(t)为由扭矩的变动分量(Tg1a(t))引起的轮齿啮合力，Fm和FaT(t)之和为扭矩引起的广义力。

齿轮动态传动误差为：

p(t)=x(t)+yg1(t)-yg2(t)-e(t)

(6)

式中，e(t)为静态传动误差。通常假设静态传动误差以啮合频率呈周期性变化，其Fourier级数展开为：

(7)

式中，ei为静态误差的i阶谐波幅值，ω为啮合频率，φi为i阶谐波初相位。

本文采用势能法[13]对kh(t)进行计算，角位移周期函数计算结果如图2所示。

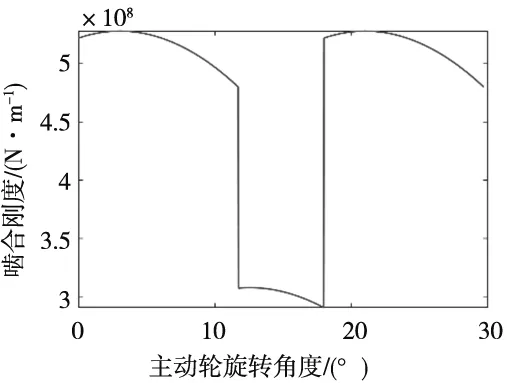
图2 齿轮啮合刚度

ch(t)一般由啮合刚度kh(t)计算：

(8)

式中，ζ为阻尼比。

1.2 理论周期时变传递函数

以扭矩引起的广义力为输入，动态传动误差为输出，两者之间的传递函数模型推导如下。

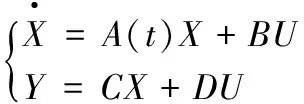
(9)

式中，

C=[0 0 0 0 1 0],D=0

式中，T为转置运算符。

对上述状态方程进行拉氏变换，负载扭矩引起的广义力和动态传动误差之间的理论传递函数为：

G(s,t)=C(sI-A(t))-1B

(10)

可见，齿轮动力学系统的理论传递函数是时变的，在匀速工况下为一类周期时变系统。

2 周期时变系统辨识方法

在匀速工况条件下，以扭矩广义力和动态传动误差分别为系统的输入输出数据，采用周期时变系统辨识理论[14]，开展齿轮系统时变频率响应函数的建模与辨识。

2.1 周期时变系统的输入输出模型

线性周期时变系统G可以由无限多个加权线性时不变系统组成的并行结构很好地描述，该结构如图3a所示。在实际中，采用有限个(如Nb)加权线性时不变系统组成的分支结构就可以较好近似系统G，即：

(11)

式中，G(ω,t)称为瞬时传递函数，Gl(ω)为谐波传递函数，ωsys为系统的时变频率，即齿轮传动系统的啮合频率。

在频域中对瞬时传递函数进行辨识，以下为辨识中需要的基本假设。

假设1(激励信号)：输入信号为随机相位多正弦信号。

(12)

式中，ωexc=2πfexc表示多正弦信号的基频，且Uk≠0，相位φk在[-π,π]区间内均匀分布，Kexc为激励频率的集合(整数的子集)，式(12)中满足Uk≠0的频率线(k∈±Kexc)被称为激励线。Nexc等于激励线的数量。

假设2(同步性)：输入应与系统时间变化同步，即：

(13)

式中，Q为有理数的集合。此外，多正弦信号的ωexc=qω0，且ω0=2π/T为信号的频域分辨率。

假设3(稳态响应)：输入u0(t)和输出y0(t)应在稳定状态下被观测。输入u0(t)和输出y0(t)具有相同的周期性，且周期T=pTsys。

在不改变系统输入输出关系的前提下，可将图3a中的时变增益模块和线性时不变模块进行交换，得到图3b所示的模型。该模型可视为多输入单输出的线性时不变系统，则其频域的输入输出关系可以表示为：

(14)

式中，U0(k)、Y0(k)为输入、输出向量的离散傅里叶变换的频谱，Hl(ωk)为图3b中模型对应的谐波传递函数，p=ωsys/ω0，且ωk=kω0。

图3 线性周期时变系统原理图

2.2 瞬时传递函数的局部多项式估计

本文采用非参数辨识方法中的局部多项式法对系统的瞬时传递函数进行辨识。局部多项式法为一种常用于多输入多输出线性时不变系统的非参数辨识方法，该方法基于光滑频率特性，在局部区间内利用多项式对频率响应函数和瞬态项建模，采用最小二乘法估计模型参数[15]。

假设噪声模型是可加的，根据式(14)，输出含噪声的线性周期时变系统输入输出关系可以表示为：

Y(k)=H(ωk)U(k)+W(k)U(k)=U0(k)

(15)

式中，U(k)为输入向量。

U(k)=[U(k-pNb)…U(k)…U(k+pNb)]T

(16)

多输入U0(k)与单输出Y0(k)之间的频率响应函数为：

H(ωk)=[HNb(ωk)…H0(ωk)…H-Nb(ωk)]

(17)

另外，误差项W(k)=NY(k)+Ys(k)，其中，NY是输出噪声；YS是输出随机非线性扰动。

在一个局部频带内，即在频率线k+l上(l=-n,-n+1,…,0,…,n)，频率响应函数H(ωk)可以被一个低阶多项式局部近似，

(18)

式中，R为多项式的阶数。

忽略式(18)中的偏差项，在频率线k+l上，式(15)可以表示为：

Y(k+l)=Θ(k)K(k+l)+V(k+l)

(19)

其中，

Θ(k)=[H(ωk),h1(k),h2(k),…,hR(k)]

(20)

为1×(R+1)(2Nb+1)的行向量且向量K(k+l)被定义为：

K(k+l)=[(1l…lR)⊗UT(k)]T

(21)

式中，⊗为克罗内克积运算符。考虑所有的频线l，将式(19)组合成矩阵方程，

Y(k)=Θ(k)K(k)+V(k)

(22)

其中，Y(k)，K(k)，和V(k)分别为1×(2n+1)，(R+1)(2Nb+1)×(2n+1)和1×(2n+1)的矩阵。

通过最小二乘法，可得：

(23)

S=KH(KKH)-1(I2Nb+1),0)H

(24)

式中为了简化符号，忽略式(24)中的频率参数k，xH为x的共轭转置。

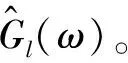
(25)

最后，瞬时传递函数的非参数估计为：

(26)

关于瞬时传递函数估计的不确定性分析以及如何确定最优的模型阶数，可参见文献[14]。

3 算例分析

3.1 模型设置

以文中1.1节所述的三自由度齿轮集中质量模型为算例验证本文方法的有效性。Tgla(t)采用随机多正弦激励，采样频率fs=215Hz，采样点数N=217，周期P=4，相位R=100，幅值A=50 N·m。时变周期Tsys=0.5 s，Tglm=200 N·m。齿轮系统具体模型参数如表1所示。

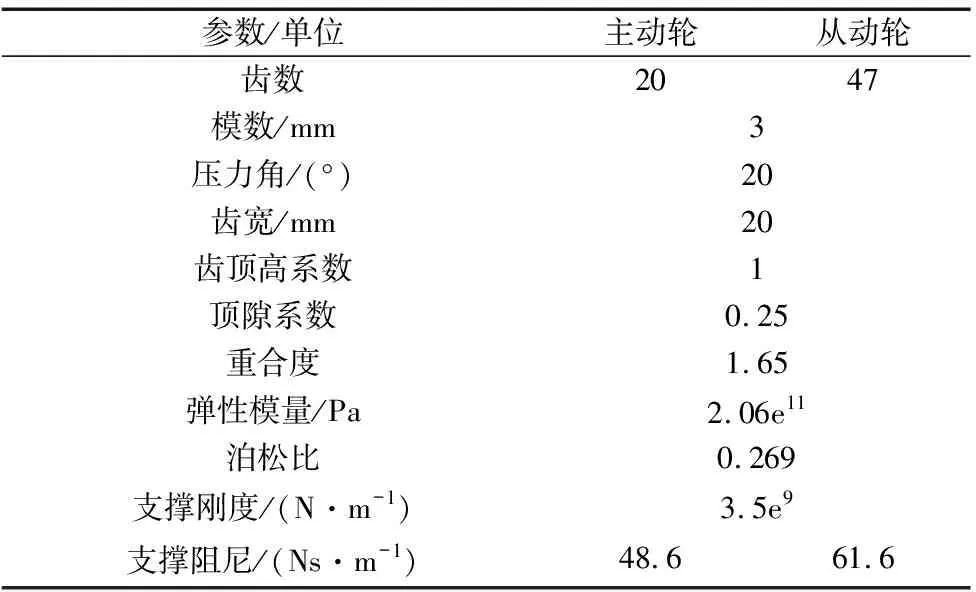
表1 齿轮系统基本参数

生成的模型输入如图4所示，利用四阶龙格库塔法求解式(1)，得到的模型响应如图5所示。

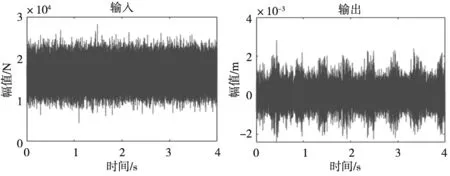
图4 负载转矩引起的广义力 图5 动态传动误差

3.2 辨识结果

本文考虑0～8000 Hz频带上的数据信息，利用式(26)辨识得到的时变频率响应函数如图6所示。

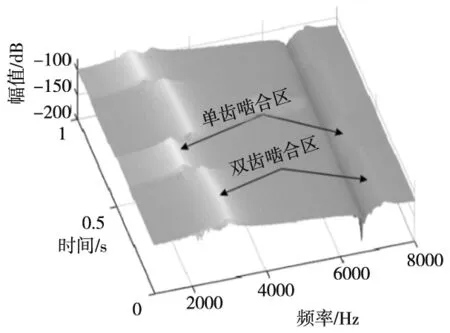
图6 频率响应函数

可发现，随着时间的变化，频率响应函数呈周期性变化。这是由于齿轮转动时，单双齿的交替啮合导致齿轮系统固有频率发生了改变。随着时间的变化，其一阶固有频率、二阶固有频率分别在2385～3011 Hz、6938～7165 Hz范围内周期性变化。

同时，由式(10)计算得到理论时变传递函数，如图7所示。

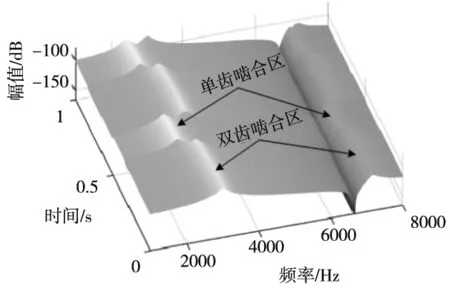
图7 理论频率响应函数

与图6的辨识结果比较可知，辨识得到的时变频率响应函数与理论传递函数吻合较好，能够准确地捕捉齿轮系统的时变特性。

4 结论

本文针对齿轮系统传动过程中典型的时变特性，提出了基于传动误差的齿轮系统时变频响函数辨识方法。以三自由度齿轮集中质量模型作为算例，验证了该方法的有效性。本文方法表现出了较高的建模精度,能够准确刻画齿轮系统的时变特性，可为齿轮系统的减振降噪、故障诊断及智能控制提供基础。结合转速测量技术，可直接拓展至处于变速状态下齿轮系统的建模与辨识。