基于幂律特性的企业用电量网络构建与中心企业分析

许荣华，胡仁杰，綦方中，马庆国

(浙江工业大学管理学院，杭州 310023)

0 引言

为解决实际问题，考察多个对象之间的联系，复杂网络成为了有效的分析工具。复杂网络是复杂性科学研究中的一个重要分支，一个典型的复杂网络由顶点和连接顶点的边组成，其中顶点代表了研究对象，而连接边代表了研究对象之间存在的关联。特别地，连接边的形成可以根据研究对象所属的具体领域以及关联关系的具体含义而改变。因而复杂网络分析已经广泛运用于技术、社会、信息以及生物等领域，其中技术领域的电力网络成为近年来研究的热点。

对于电力网络的研究主要分为两类，1)使用真实的电力物理运输网络，通过研究复杂网络线路的拓扑结构的改变，来研究电力网络在停电事故中表现出的脆弱性[1]；2)考察不同行业、地区或企业用电量之间的逻辑联系，包括因果关系和相关关系等，通过最小生成树(MinimumSpinningTree, MST)、层次树(Hierarchical Tree, HT)、聚类分析等方法，考察用电量网络的多种结构和特性。Zhou等人[2]使用上海市不同行业的用电量数据建立行业用电量关系网络，并利用MST和社团发现对不同行业网络进行聚类分析，以此揭示行业间的联系。Yao等人[3-5]分别使用Granger因果关系检验[6]、Pearson相关性以及偏Granger因果关系[7]，对中国南方各省建立行业用电量关系网络，通过网络拓扑结构分解，核心顶点的考察，层次聚类[8]的应用，探究各省行业间的相互联系。Xiao等人[9]对欧洲电力市场建立因果关系网络，并使用方差分解的网络拓扑确定影响其欧洲用电量结构稳定的因素。

对用电量网络的研究不仅可以展现行业或地区间联系，作为城市基础指标，用电量网络的宏观分析能够进一步反映城市经济发展状况及其发展中心。Kantar等人[10]通过MST和层次树方法展现了亚洲高经济收入国家有更高可能性处于网络的中心，并发现高经济收入国家的用电量变化与其GDP增长相吻合。网络的宏观分析包括网络拓扑结构分析，很多学者通过网络拓扑测度来反映经济状况。Tang等人[11]通过探究聚类系数、介数中心性等测度，发现美国与中国的金融网络拓扑存在明显差异，揭示现实中两个国家市场行为的区别。Hu等人[12]通过设定阈值和MST构建各产业经济网络，显示不同产业形成的网络结构差异较大，反映了不同产业在经济系统中的差异。除了网络整体结构特性与经济增长形成关联，在网络结构中处于核心位置的中心顶点还展现出了对经济增长的带动(或抑制)作用。Li[13]等人通过建立世界国家贸易无标度网络，发现美国作为加权度分布的最大顶点，大多数其他国家与美国存在显著的经济周期同步。Lee等人[14]发现面对金融危机，国际贸易网络中与外界连接紧密的顶点集团会加剧危机的蔓延。

在对电量网络的研究中，大多数学者通过网络连接结构(如MST形成的星型结构等)来找到中心顶点[2-5,15]，但是这类顶点只代表了网络的局部中心，且只能体现单一中心对其邻居顶点的影响。考虑同时展现网络所有中心顶点的连接情况，复杂网络中的幂律分布性质能够为我们提供较好的分析角度。网络度分布是否满足幂律分布特性是复杂网络分析中的重点问题，在许多领域中都对幂律分布做出了研究。Clauset等人[16]提出了完整的幂律分布考察及计算方法，并将其运用在各个领域中。Rho等人[17]考察了不同临界值下的网络度分布特征，发现在一定的阈值下度分布将服从幂律分布。在此基础上，Yang等人[18]在金融领域网络度分布的研究中进一步说明了形成幂律分布特征所需满足的阈值条件。

与随机网络相比，符合幂律分布的网络存在更强的规则性。头重分布作为幂律分布中的重要性质，指网络中大部分的连接仅指向小部分度数较大的顶点，Newman[19]在研究中提出了度大顶点比例P和与其相连边数比例W之间的关系，通过这种关系可以近似估计网络中顶点与连接分布特征。Lorenz[20]在此基础上研究了不同幂律系数取值下P和W之间关系的变换，即洛伦兹曲线。洛伦兹曲线的建立可以清楚了解网络中顶点和连接边的变化趋势。

基于学者们对阈值和幂律分布的研究，本文考虑使用幂律分布作为用电量网络中阈值选择的标准，运用幂律分布的拟合情况和阈值相结合的方法，确定相关系数阈值，从相关性矩阵中过滤出中心企业及其连边，建立中心企业用电量相关性网络。本文使用杭州市2017工业企业用电量数据，分别通过头重分布、同配混合特性、小世界特性等方面对企业用电量相关性网络进行实证分析。

1 数据描述

自从第11届G20峰会在浙江省杭州市召开，杭州城市建设和经济加速发展，超出了以往任何时期。特别地，杭州市规模以上工业增加值的发展速度在2017年到达顶峰。2017年是杭州近年来快速发展的典型时期，从企业用电量关联特性的角度对杭州城市发展做出实证分析，本文收集了杭州2017年总共1 788家工业企业的日用电量时间序列数据，数据来源于国家电网浙江省电力公司。选择工业企业日用电量的原因有：

1)工业用电量在城市全社会用电量中占有较大的比重，相比于全社会用电量，其变化会受到居民用电量的影响，仅使用工业用电量能更及时地反映城市经济发展状况。

2)日用电量的变化及时，相比较其他更新周期，如月用电量、季度用电量，更短的记录间隔意味着更准确的分析。

图1描述了企业数据天数(总天数为334天)的累计分布，以及数据缺失(天数在334天数以下)的企业频次分布图。其中，大图表示企业天数累计分布，x轴表示天数，y轴表示累计频率；小图展示了仅包含部分天数的企业，x轴表示天数，y轴表示企业数目。鉴于我们的数据时间跨度，总共为334天，大多数企业保留了完整的记录天数，仍存在大约20%的企业未达到标准。为保证数据的有效性，我们仅保留拥有完整记录天数的企业，总企业数为1 469。

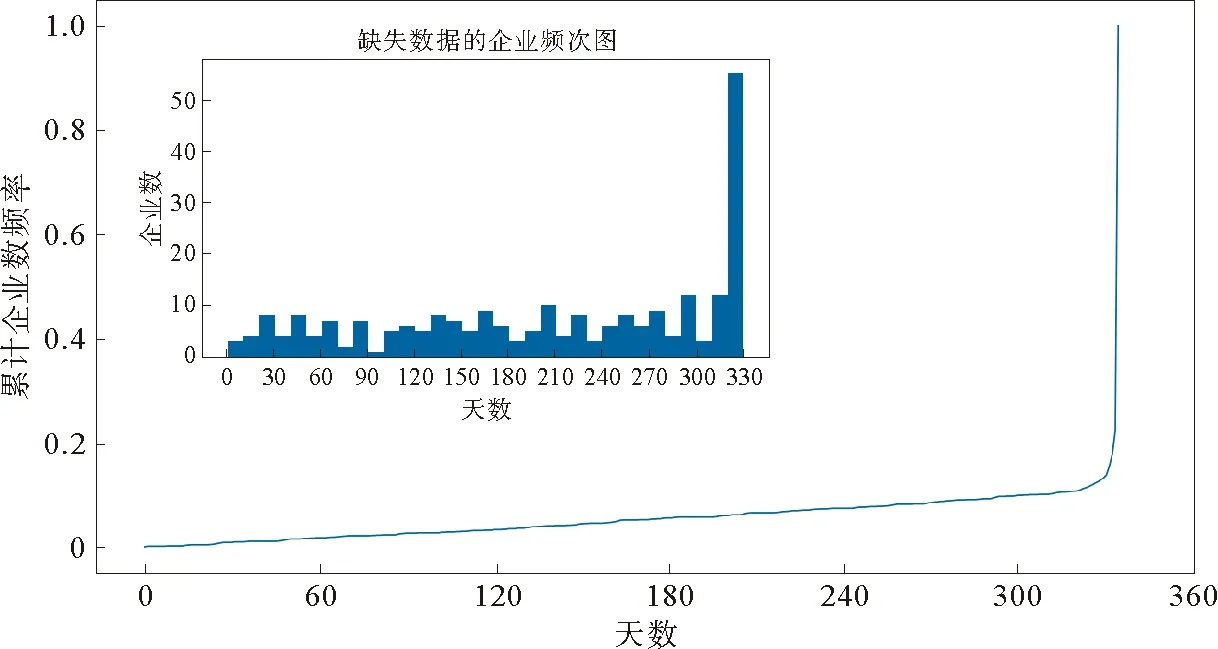
图1 企业天数累计分布与334天数以下企业分布

2 网络模型建立

2.1 条件Pearson相关性

Pearson相关性检验作为检验两组数据之间的线性相关程度的有效工具，在金融、医学[21-22]等领域都有非常广泛的应用。同样地，也可以用于考察两组时间序列数据之间的相关性，比如股票走势[23]、电量变化等。

在时间序列分析中，数据的走势会呈现出一定的规律性。本文使用企业用电量的日增变化率来衡量该企业用电量的走势变化，即：

(1)

Ei·t为企业i在第t天的用电量，ei·t+1为企业i在第t+1天相对于前一天的用电量增长率。

企业用电量除了反映企业自身的发展变化，还会随着季节变化产生明显波动。由于这种影响的存在，大部分企业的用电量存在同步变化，进而形成虚假的线性相关关系。因此需要排除用电量数据中的季节因素，还原企业自身真实用电量的变化。本文定义该城市宏观基础用电量为所用企业日用电量之和，即：

(2)

相应地，该城市宏观基础用电量的日增变化率为

(3)

因此，观察到的企业用电量变化的来源可以分解为两部分，一部分是所有企业都会受到的宏观因素影响，表示为eI；另一部分是企业自身发展产生的用电量波动。

在统计学中，通过建立回归模型，用自变量的变化解释因变量的变化。本文使用宏观基础用电量的日增变化率作为自变量，对每个企业的用电量日增变化率建立线性回归模型:

ei·t=a+b*eI·t+εi·t

(4)

由于随机扰动的存在，计算得到的预测值与观测值会产生偏差，因此，残差表示了自变量无法解释因变量的部分。通常，使用最小二乘法寻找最小残差平方，来确定最佳的拟合函数。使用宏观基础用电量的变化对企业用电量的变化进行回归分析，残差反映了由企业自身因素产生的用电量变化，其定义为

(5)

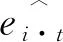
我们将所有企业的原始用电量变化率数据转化为残差数据，再进行两企业之间的相关性检验，得到两企业间的条件Pearson相关系数Cij：

(6)

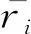
通过对所有企业进行条件Pearson相关性检验，得到企业用电量相关性矩阵C。图2描述了企业相关系数的分布图。一般地，可以根据相关系数将相关性强度分成5个等级：1)绝对值在0.8～1.0表示极强相关性；2)0.6～0.8表示强相关性；3)0.4～0.6表示较强相关性；4)0.2～0.4表示弱相关性；5)0～0.2表示极弱相关性[24]。

两两企业之间(排除企业自身)的相关系数从最小值-0.75到最大值0.96不等，企业之间的相关系数集中在-0.2到0.4之间。根据图3累计频数分布图的结果，网络中的强负相关关系仅存在于网络中极小的部分，因此本文只考虑强正相关部分。图2显示，随着相关系数的增加，累积频率以逐渐降低的速度逐渐增加到1，并且大约90%的企业相关性小于0.6，表明大部分企业之间的相关性较弱。

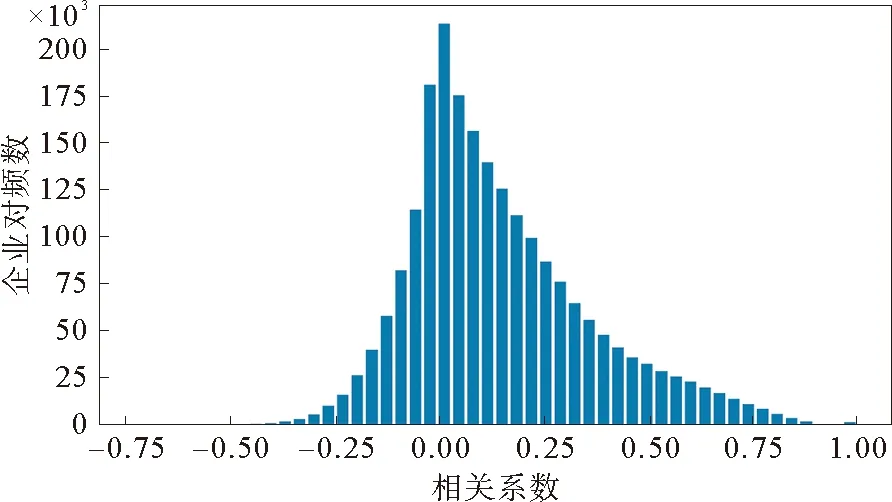
图2 企业条件Pearson相关系数分布图

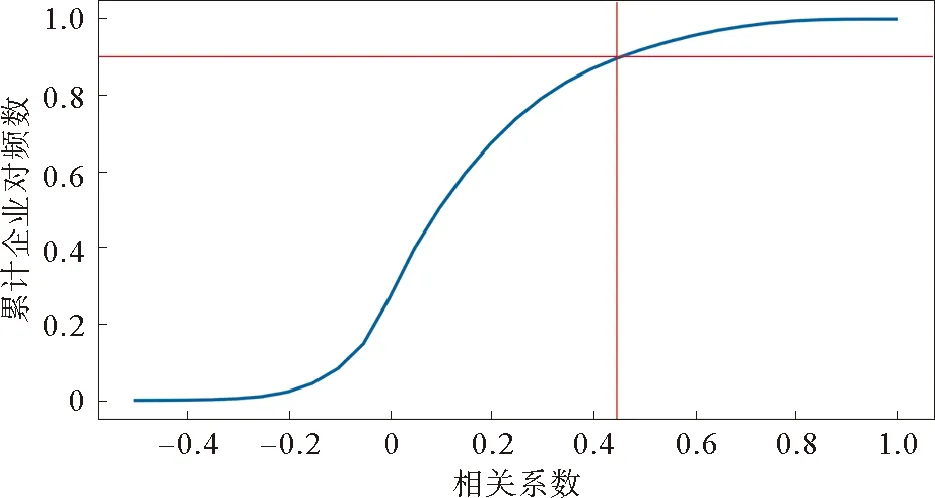
图3 企业条件Pearson相关系数累计分布图

2.2 网络幂律分布

复杂网络一般具有3个特征：1)小世界，网络规模即使再大，两顶点之间总能找到一条极短的路径；2)集群性，网络中的顶点总会产生聚类状态；3)如果网络的度分布满足幂律，网络顶点度数与拥有该度数的顶点所占比例之间存在如式(7)的函数关系。

pk=ck-α

(7)

其中，k表示顶点的度数，pk表示度为k的顶点所占比例，α为该分布的幂律系数。幂律分布是大量复杂系统研究的重点，涉及大量研究领域，比如天文、社会、计算机等[25-27]。满足幂律分布的网络中大量的连接仅存在于少数顶点中，这些顶点为网络的中心顶点，而大部分顶点只有很少量的连接。少数中心顶点对网络的运行起着主导的作用。

由于两两企业用电量之间总存在一定相关性，以相关性矩阵C建立的全连接网络度分布无法满足幂律。由于网络中存在大量相关性较弱的连接，具有强连接的中心结构会被大量噪声所淹没，因此需要设置阈值来过滤这部分噪声。随着阈值的增加，越来越多的噪声会被过滤，网络度分布逐渐满足幂律分布。在阈值设置后，大量的顶点与外界仅有少量的强连接。

相关系数矩阵C可以通过如式(8)的规则转化为筛选后邻接矩阵D：

(8)

其中，Cr表示相关性系数阈值。

由于用电量网络中的连接复杂，因此本文使用双对数线性回归模型来考察网络度分布是否近似满足幂律。基于式(7)，将pk转化为实际顶点数后，两边同时进行对数变化，即可得到：

logNk=-αlogk+logc

(9)

其中，Nk表示度数为k的顶点数。本文使用最小二乘估计方法来判断该数据是否近似服从幂律分布。

考虑到低相关系数连接会掩盖核心连接结构，强相关性连接更能有效反映顶点之间的关系，因此本文仅考虑网络中强相关系数0.7以上的连接。图4和图5描述了杭州市企业用电量网络在阈值0.7和0.8条件下的双对数分布图。图4和图5中x轴和y轴分别表示度数和相应顶点数的log对数变换，省略了没有任何邻居的独立顶点。当阈值大于0.7时，在双对数分布图中近似呈现出线性趋势，模型拟合优度R2达到0.543，自由度为898。随着阈值的增加，越来越多的顶点被过滤，线性回归拟合优度逐步上升，在0.8阈值下，模型拟合优度R2达到0.686，自由度为491。

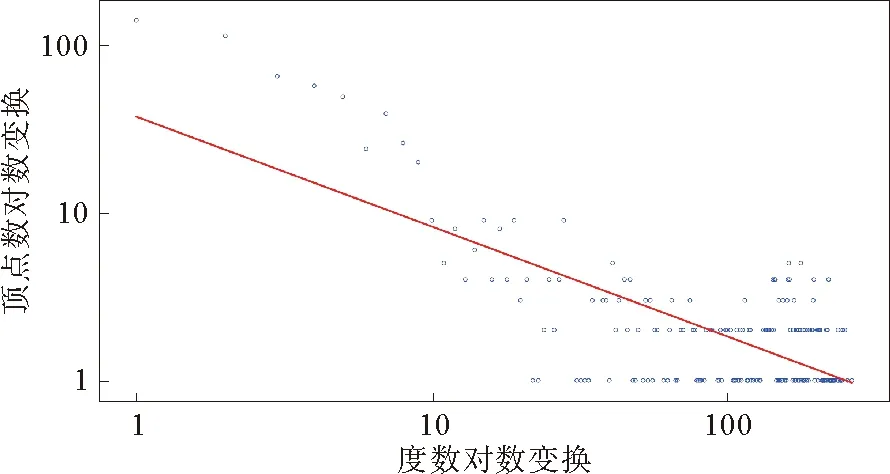
图4 阈值为0.7时的双对数度分布

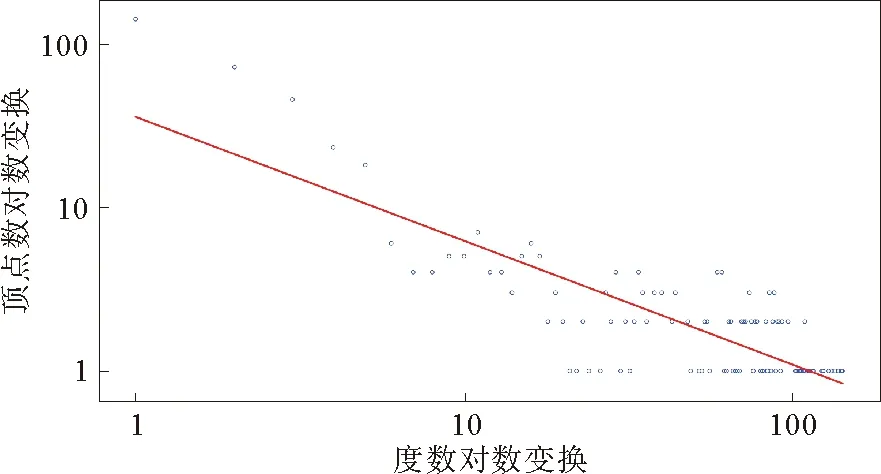
图5 阈值为0.8时的双对数度分布

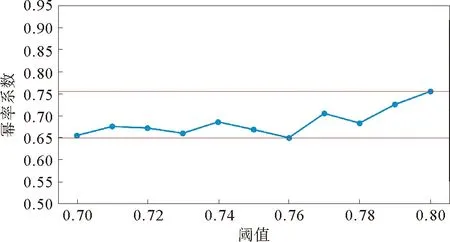
图6 不同阈值下幂律指数分布

以0.01阈值为间隔，图6描述了0.7到0.8之间各阈值取值下网络度分布的幂律指数分布。其中x轴和y轴分别表示相关系数阈值和相应的幂律系数。在阈值设定0.7～0.8时，度分布近似符合幂律分布，幂律指数α大致稳定在0.65和0.75之间，由于变化程度很小，可以认为在这些阈值下的网络度分布服从同一幂律。在0.7～0.8区间内的幂律指数均值为0.676。另外，我们经过测试发现，当阈值超过0.8后，幂律指数迅速上升，原因在于较大的阈值排除了大量噪声，仅有的用电量网络度分布逐渐形成近似完美的幂律分布，在阈值设置为0.87时，幂律分布效果最好，回归模型拟合优度R2达到0.861，但是企业连接数随之大量减少。经过测试，在阈值设置为0.84时，网络中有邻居顶点的企业数下降到总企业数的20%；阈值达到0.87时，网络中有邻居顶点的企业数仅不到5%，企业数量过少会影响对网络连接总体分布的分析。因此本文只考虑阈值区间在0.7和0.8之间的情况。

3 头重分布分析

对于度分布近似满足幂律分布的网络，会满足另一种独特的分布特性，即头重性质：网络中大部分的顶点度数较小，而小部分的顶点拥有网络中大量的连接。考察头重分布特性能够对网络进行整体分析，识别网络中处于中心位置的节点，进而重点研究这类中心节点的连接情况。作为头重分布的常见例子，在大量事实中发现有很多现象满足80/20分布，简称二八定律，是帕累托分布中一种常见实例[28]。比如：在经济领域，其认为社会上20%的人拥有了80%的财富。

二八定律认为小部分个体就可以对总体起着主导作用，因此定律中的20%是研究的重点。在满足幂律分布的网络中这类中心节点对于城市整体经济发展起着主导作用。由于大部分节点连接到了小部分中心节点中，小部分中心节点能够较大程度地联系整个网络，进而促进企业间信息及资源传播，决策者也可以通过重点干预中心顶点而促进整体网络的发展。然而拥有头重性质的网络存在较强的脆弱性，攻击中心顶点会使网络连接破碎，因此在现实中同样需要对中心顶点进行保护，以保证网络连接。

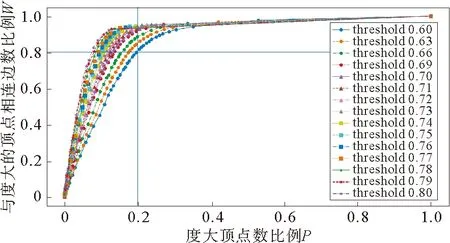
图7 不同阈值下度大顶点数比例P与相应连接边数比例W的累计分布

为考察杭州市企业用电量网络中顶点与其边数之间的分布关系，我们使用如下测度：假设网络中度较大顶点占总顶点的比例为P，与这些顶点相连的边数占总边数的比例为W，Lorenz[20]研究了在不同幂律指数α下，W和P的关系曲线变化，称为“洛伦兹曲线”。Newman[19]提出了在完美幂律分布下W和P的关系。不过，现实中大多数网络均仅近似满足幂律分布，因此本文从P和W的定义出发，考察网络中顶点和连接的分布关系。图7绘制了各阈值下P和W的累计分布曲线，反映了不同阈值的曲线变化。

其中，x轴为度大顶点数比例，表示度数排名前P位的顶点；y轴表示与这部分顶点相连的边数占网络总边数的比例。以P=0.2,W=0.8为例，表示网络中度数在前20%的顶点拥有网络中80%的连接数，即二八定律。对于不同阈值下的曲线，均保持上凸的形状。当P值处在0.1～0.2之间时，曲线上升速度非常快，意味着大部分的边只与少量的顶点连接。特别地，随着阈值的增加，曲线的上升速度也随之加快。以此说明杭州工业企业用电量网络，在强相关性0.7～0.8的条件下，大约20%～10%的企业拥有网络中大约80%～90%的连接，即仅有小部分企业涵盖了网络中大部分的强相关关系。这些小部分企业构成了城市的中心，影响着城市中的大部分企业。接下来，将重点围绕中心企业构成的用电量网络，探究在不同阈值下中心企业网络连接情况。

4 中心顶点分析结果

4.1 中心顶点选择

通过第3节洛伦兹曲线的建立，我们发现杭州企业用电量网络中，绝大部分连接仅由小部分顶点决定，这些顶点被看作是网络的中心顶点。在给定阈值条件下，网络度大顶点和其连接数形成了明显的二八分布。随着相关系数阈值的上升，度数前20%的顶点能够拥有更多的连接，表示网络中的强相关性均与这部分中心顶点有关。

为探究中心顶点对其他顶点的直接影响，我们将度数前20%的顶点作为中心顶点，建立中心顶点及其直接邻居组成的相关性网络。图8和图9分别展现了在阈值设置为0.7和0.8时建立的网络。

图8 阈值设置为0.7时的20%度大顶点(圆形标注)及其直接邻居组成的相关性网络

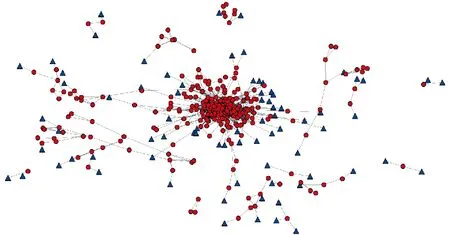
图9 阈值设置为0.8时的20%度大顶点(圆形标注)及其直接邻居组成的相关性网络

其中圆形顶点表示度数前20%的度大顶点，即中心顶点；三角形顶点为中心顶点的直接邻居顶点。该网络仅包含有一个连通分支，网络呈现出明显的从中心向外发散的结构。我们发现中心顶点之间存在非常复杂的连接，而且这种内部联系，在数量上远远高于他们与邻居顶点的联系。因而我们通过计算中心顶点的邻居仍为中心顶点的概率，考察中心顶点之间和与其他顶点之间的连接关系。图10描述了不同阈值下的概率。其中横线表示多种不同阈值下的概率均值，数值是0.939。结果表明中心顶点有90%以上的邻居依然为中心顶点，概率数值随阈值变化波动较小。从以上结果得知，中心顶点与中心顶点之间的内部连接众多且紧密。

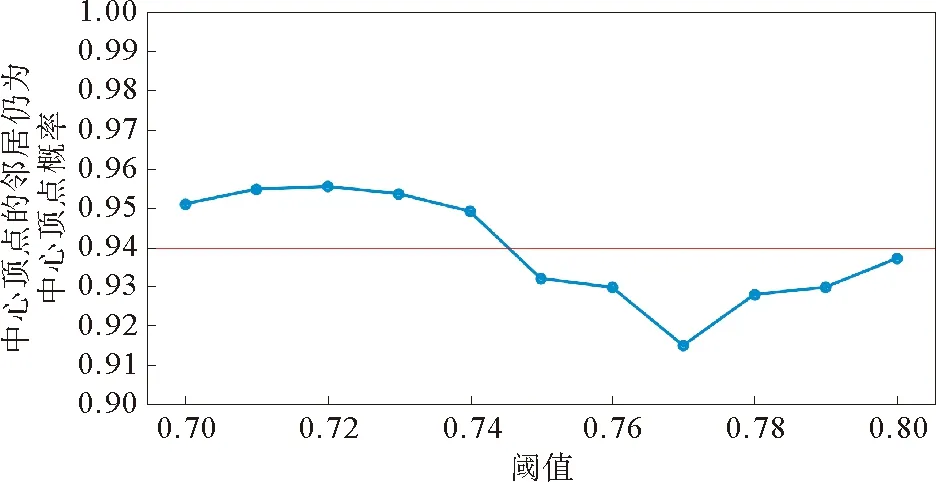
图10 中心顶点的邻居仍为中心顶点概率

另一方面，本文研究了网络的同配混合性质。同配混合是指在网络中的顶点倾向于与同种属性的顶点连接，也可称为同质性[29]。相反，如果网络展现出异配混合的结果，说明网络中的顶点更倾向于与不同属性的顶点连接。

通过计算同配系数判断网络是否同配，其取值在-1～1之间：如果同配系数为正，表明网络属于同配混合；如果为负，则属于异配混合。本文分别对20%度大顶点及其邻居顶点设置不同的属性，并且计算不同阈值下的同配系数。表1给出了不同阈值下网络同配系数的结果。

可以清楚地发现：在0.7～0.8的阈值下，同配系数均大于0，尽管数值不大，但是足以表明网络满足一定的同配混合性质。我们可以将阈值看作来自外界的攻击，由于满足头重分布的网络具有脆弱性，因此随着阈值的增加，中心顶点之间的连接变得稀疏，网络开始破裂，对内连接与对外连接逐渐相当，进而同配混合系数逐渐减小。当阈值为0.8时，同配系数接近于0，网络此时均不满足同配或异配特征，说明中心企业之间的相关关系大部分处于0.7～0.8之间。

另外，特征向量中心性也是考察网络中心的一种常用测度[30]，Bonacich[31]提出，一个节点的中心程度不仅在于其邻居的数量，还在于其邻居的中心性程度。连接到少量却重要的邻居的节点具有较高的特征向量中心性，而如果一个节点只拥有较低重要性的邻居，其得分就会小得多[32]。由于考虑了邻居的重要程度，因此度中心性高的节点不一定具有较高的特征向量中心性。本文分别计算了网络中20%度大顶点以及其余所有非独立的特征向量中心性，发现有超过80%的非中心顶点拥有极小(小于0.001)的特征向量中心性，表2汇总了不同阈值下20%度大顶点与所有非孤立顶点(包含前者)的平均特征向量中心性。我们发现中心顶点的平均特征向量中心性始终大于所有非孤立顶点的计算结果，说明中心顶点普遍拥有较高的特征向量中心性。

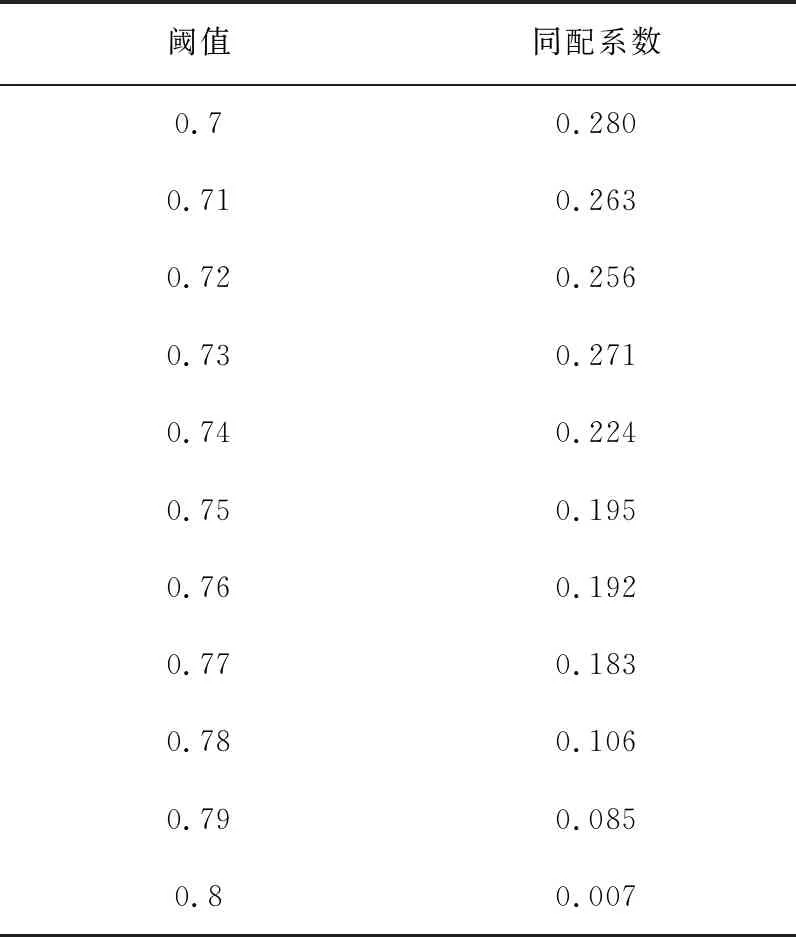
表1 不同阈值下网络同配系数计算结果

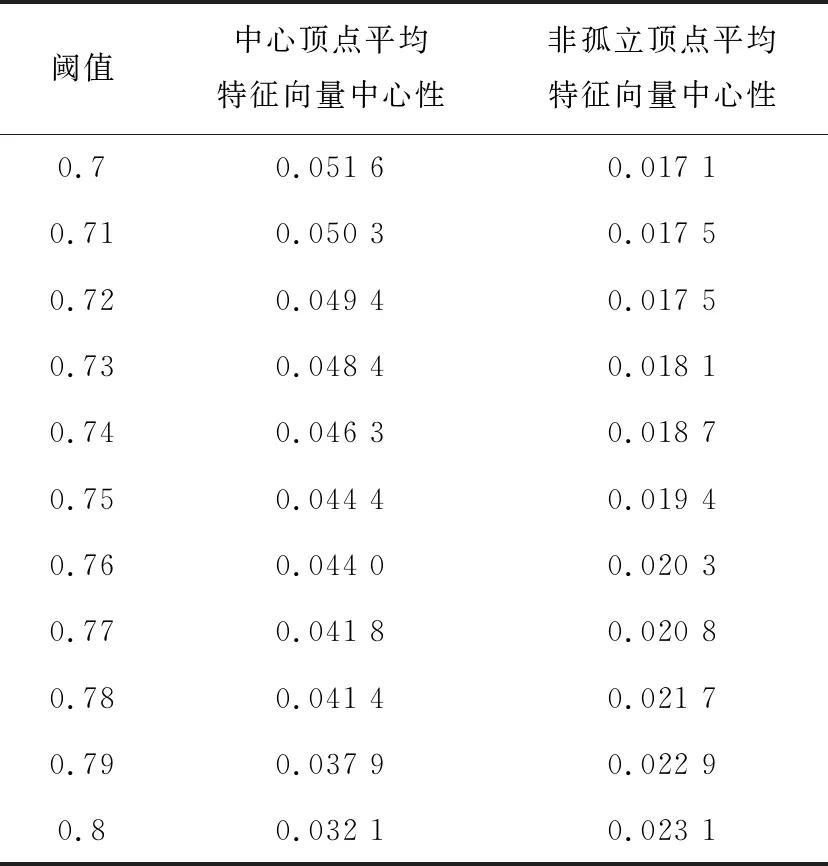
表2 不同阈值下中心顶点和所有非孤立顶点(包含前者)的平均特征向量中心性

另外，本文分别将两组顶点根据中心性降序排列，并绘制散点图。在0.7阈值下的结果如图11所示，图中圆形标记代表所有顶点的特征向量中心性排序，三角形标记表示中心顶点排序。我们发现三角标记能够很好地与圆形标记重叠，仅在尾部出现偏差，表明有超过95%由度数选择到的中心顶点，依旧拥有较高的特征向量中心性。随着阈值的上升，也能得到类似的结论。因此中心顶点不仅拥有广泛的连接，连接到的其他网络节点也拥有较高的中心性，结合中心顶点对内连接大于对外连接的结论，进一步说明了中心顶点的重要性。

通过对中心企业与其邻居企业的连接关系、网络同配系数以及特征向量中心性的考察。清楚地表明：在一个城市中存在用电量高度相关且网络结构高度同质的少部分企业，包含了该城市企业大部分的相关关系，并且这些企业内部之间形成了紧密而有效的合作关系，成为城市的中心企业。

在上述分析中，我们发现这样两个问题：

1)在0.8阈值条件下，同配系数虽然表示网络不符合同配混合性质，但在网络的最大分支中仍然能够发现部分中心顶点之间紧密联系，且大于对外的连接。

2)随着阈值的上升，中心企业之间被分成了多个分支，这些分支以一个最大分支(涵盖了大部分中心企业)和多个小分支组成，形成了明显的核心—边缘结构。因此，在极高阈值条件下，一些中心企业从网络中心脱离了出来，失去了代表性。

进而，我们要找到网络中最关键的中心企业，这些企业之间总是存在紧密连接，不会因为相关系数阈值变化而破裂。通过试验，我们发现在0.7～0.8的阈值条件下，度数前10%的顶点均能够保证产生单一分支的网络。如图12展现了在阈值设置为0.8时，10%度大顶点及其直接邻居顶点组成的网络。

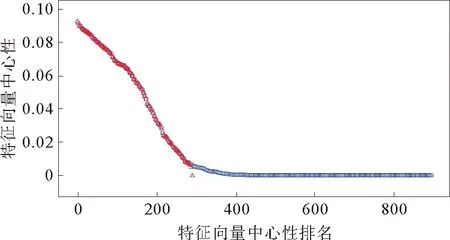
图11 网络非独立顶点与中心顶点的特征向量中心性排名

我们发现10%度大顶点全部来自于20%度大顶点形成的网络最大分支中，即尽管同配系数为0时，网络中仍然连接紧密的部分。而且我们发现在0.7～0.8的阈值下，前10%的度大顶点涵盖的企业基本保持不变，即大约147家固定企业之间存在有大量的0.7～0.8以上的强连接。由于在0.7～0.8的阈值条件下，中心企业能够满足同一分支的条件，说明当其他企业与这部分中心企业连接时，能够进入到企业联系最中心的部分。以此我们认为10%度大顶点对试图与中心企业产生联系的其他企业具有更加重要的作用，称其为关键企业。

4.2 小世界特性

小世界效应首先在社会网络中发现，研究者Milgram[33]通过信件传递试验发现任意两人之间最多只需要6步即可产生联系，说明现实生活中信息能够形成快速的传递。在不同的领域中小世界有着不同的实质意义，比如在社会网络中意味着两个人之间的信息需要传递的次数；在交通、铁路、航空网络中意味着两地之间中转站数等等。特别地，在电量相关性网络中，我们认为两企业之间的用电量相关性代表了紧密的合作关系与供应链关系，因此小世界特性意味着两企业之间能够更快地进行资源传递、信息交流。

小世界效应的测量主要在于网络的平均测地距离和网络聚类系数。测地距离是指两顶点之间的最短距离；聚类系数是指网络中三顶点之间形成闭合三角形结构的比例。表3描述了阈值设置在0.7～0.8时，平均测地距离、网络聚类系数以及网络直径的信息。

可以看出该网络拥有较小的平均测地距离，以及较大的聚类系数，说明该网络满足小世界特性。尽管随着阈值的增加，网络中的极强连接关系减少，从而导致平均测地距离增加，聚类系数减少，但是网络直径，即网络中

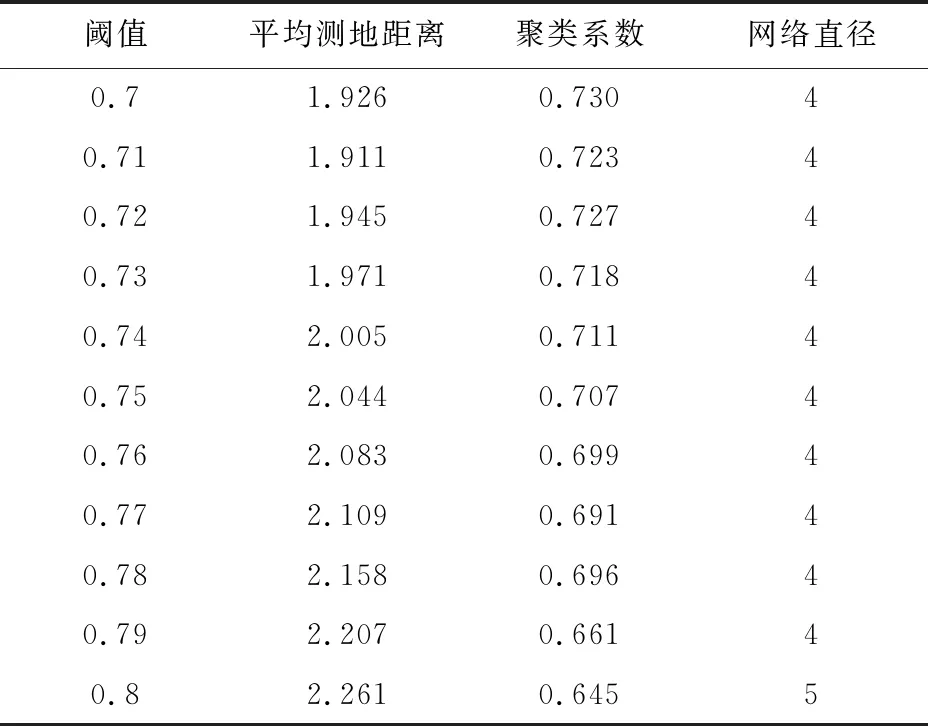
表3 不同阈值下的平均测地距离、聚类系数以及直径计算结果

最大的测地距离没有产生较大变化，说明网络中顶点之间的连接依旧保持着较高的密集程度。考虑到极小的平均测地距离，说明在10%度大顶点的邻居之间，平均只需通过1～2个关键顶点即可形成联系。特别地，当我们删除关键顶点时，邻居顶点以及其他非独立顶点之间的平均测地距离，在0.7的阈值条件下，上升到了3.784，聚类系数下降到了0.596。表明关键顶点的存在，加快了企业信息及资源的传播。

大部分企业由于与外界连接较小，或者连接较弱，往往无法成为网络的中心。因此这些顶点在企业间信息传递、资源共享等方面，仅依赖于少数企业，存在信息不充分的劣势。中心企业作为城市的中心，两两之间存在大量的强连接，形成了强关系网。其中10%度大顶点，即关键顶点，能够在相关系数0.8的强条件下保持单一分支的网络结构，并且满足小世界特性，意味着关键顶点能够促进企业之间联系。对于企业来说，与这些关键企业相连接，可以增加信息来源数量，加强资源共享效率。对于城市来说，关键企业如同城市企业发展的“风向标”，进一步刺激这些关键企业与其他企业形成联系，扩大中心企业数量，形成更大的合作关系网络，进而促进城市发展。

5 结语

本文以杭州市2017年工业企业用电量数据为例，以企业为顶点建立网络，在使用条件Pearson相关性检验方法提取出由季节和节假日等宏观因素带来的基础电量变化后，以条件Pearson相关系数作为两企业之间的关系测度，我们发现大约90%的企业相关性小于0.6，企业间连接普遍较弱。我们通过网络度分布能否近似满足幂律分布为标准，设置相关系数阈值，发现在0.7～0.8的阈值水平下，网络度分布近似服从同一幂律，而更大的阈值会使得网络中有邻居的顶点数过少而影响后续分析。

为测量网络整体，我们通过幂律分布的头重性质考察了用电量网络中度大顶点比例与相应的连接边比例之间的关系。我们发现在阈值设置为0.7及以上网络的度分布能够很好地满足二八分布，并且随着相关系数阈值的增加而拟合程度增强。我们建立了中心顶点及其邻居的组成的网络。通过对中心顶点的邻居以及网络同配性质的考察，我们发现中心顶点90%以上的邻居依然是中心顶点，且网络满足较强的同配混合性质，意味着中心顶点之间形成了非常密集的强相关集群。特别地，度大顶点也拥有较大的特征向量中心性，进一步说明了中心顶点的核心地位。另外，10%度大顶点，即关键顶点，及其邻居形成的网络满足小世界特性。关键顶点的存在，加快了企业信息及资源的传播。对于企业来说，与这些关键企业相连接，可以增加信息来源数量，加强资源共享效率。对于城市来说，进一步刺激这些关键企业与其他企业形成联系，扩大中心企业数量，形成更大的合作关系网络，进而促进城市发展。