基于多种社交关系的概率矩阵分解推荐算法

公翠娟，宾 晟，孙更新

(青岛大学数据科学与软件工程学院,山东 青岛 266071)

0 引言

随着大数据时代的到来，数据冗余严重干扰了人们获取有效信息。推荐系统很好地解决了这一问题，成为相关领域的研究热点。推荐系统根据人们的兴趣爱好、需求信息以及消费行为等[1]，为用户推荐其可能感兴趣的商品或者信息。目前，推荐系统广泛应用于各行各业，如亚马逊的商品推荐，iTunes的音乐推荐，Netflix的电影推荐等。目前，推荐系统采用的算法主要分为三类：协同过滤的推荐算法[2-3]、基于内容的推荐算法[4]和混合推荐算法[5]。其中，协同过滤推荐算法是目前应用最广泛的，它又分为三类：基于用户(user-based)的协同过滤推荐算法[6]、基于项目(item-based)的协同过滤推荐算法[7]和基于矩阵分解(matrix factorization)的协同过滤推荐算法[8]。基于矩阵分解的协同过滤推荐算法因在Netflix Prize大赛上的突出表现被越来越多的研究人员所关注，该算法将用户对商品的评分以矩阵的形式表示，将矩阵进行分解来挖掘低维隐特征空间，进而得到两个低维的用户特征矩阵和商品特征矩阵，最后通过两个低维的特征向量的内积来刻画用户与物品之间的关联性。虽然上述推荐算法得到了较好的推荐结果，但是用户商品评分矩阵存在数据稀疏性以及分布不均等特点，导致推荐准确率低、冷启动等问题。

针对上述问题，研究人员引入外来信息并在一定程度上较好地改善了推荐结果，物品内容的描述与评论信息为物品增加了有用的信息保障；或者其他领域的信息同时服务于用户和商品也会对推荐的结果造成影响。由于传统的推荐算法忽略了用户之间的社交关系对于推荐结果的影响，社交关系能够体现出用户之间喜好的相似性，单纯考虑用户对商品的评分已经不能满足推荐的需求，因此将社交关系引入推荐系统中的社会化推荐算法成为当前推荐系统研究的热点[9]，从最初直接利用用户间的直接社交信息，到近年来通过相关算法获得用户间的间接关系构建模型进行推荐，都大大提高了推荐的准确率。根据社交推荐模型的构建方式对其梳理：1)依据用户社交关系，改变当前用户的隐性变量；2)同步分解评分矩阵和社交矩阵获取推荐隐性变量。

对于社会化推荐算法，最早可追溯到1997年Kautz等人提出的ReferralWeb系统[10]，其在传统协同过滤模型上融合社交网络，为用户提供了更加准确的推荐结果，由此证明融合社交关系为推荐系统提供了更加可靠的数据，同时为社会化推荐算法提供了新思路；Yang[11]等人采用矩阵分解技术，根据用户的信任关系将其映射到低维潜在特征空间，目的是更准确地反映用户的相互影响，有效地提高了推荐的准确性；李镇东[12]等人提出了一种以单调饱和函数为权，利用目标用户和其他项目共同评分个数相对用户总数值的真切值作为传统相似度系数的加权二部图推荐算法；曹玉琳[13]等人通过标签的相似性来计算用户之间和资源之间的相似性，进行近邻选择，提出了一种融合社会标签的近邻感知的联合概率矩阵分解推荐算法，有效利用标签的语义性提高了推荐质量；王瑞琴[14]等人借鉴社会心理学中的信任产生原理，基于用户信誉度的信任扩展方法，缓解数据的稀疏性问题，提出了一种信任加强的矩阵分解推荐算法；Ma[15]等人基于用户特征矩阵共享表示的方法，提出了一种基于用户特征矩阵共享表示的社交推荐模型，有效提高了推荐的准确性。

大多数社会化推荐算法只是引入一种社交关系，但是加入的每一种社交关系对推荐结果的影响是不同的，所以引入一种社交关系肯定会影响推荐结果的准确性。为了解决这一问题，本文基于多子网复合复杂网络模型构建多关系社交网络[16]，利用共享用户特征矩阵，将多种社交关系引入推荐系统，提出了一种融合多种社交关系的矩阵分解推荐算法。

1 传统的矩阵分解推荐算法

1.1 问题描述

假设推荐系统中包括m个用户和n个商品，Rm×n=[Rij]m×n表示用户—商品评分矩阵，如图1所示，Rij代表用户i对商品j的评分，其中Rij∈[1,5]，通常Rm×n中有许多空元素，导致用户—商品评分矩阵是一个非常稀疏的矩阵。

在社交网络中，如图2所示，用户之间的社交关系可以用矩阵C表示：C=[Cik]m×m，Cik的值为0或1,0表示用户之间不存在社交关系，1表示用户之间存在社交关系。

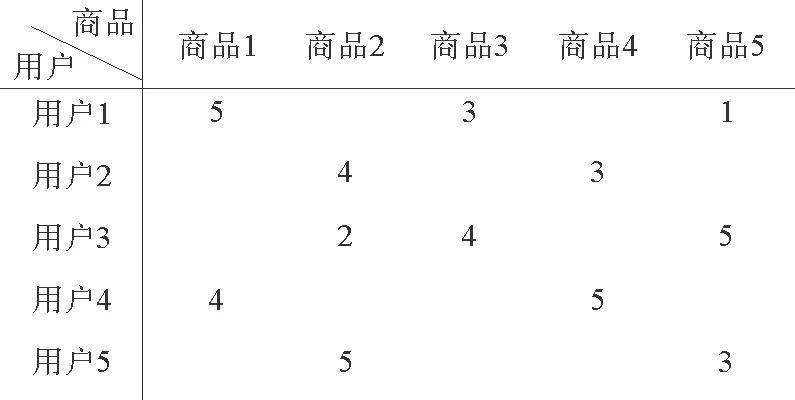
图1 用户商品评分矩阵Fig.1 User item rating matrix

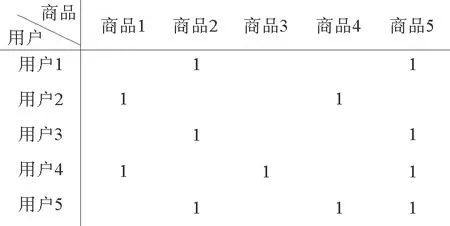
图2 用户社交关系矩阵

1.2 传统的矩阵分解模型

传统的矩阵分解算法[17]模型如图3a所示，用户商品评分矩阵Rm×n被分解成两个低维的特征矩阵Um×k，Vk×n，分别表示用户特征矩阵和商品特征矩阵，其中k表示向量的维数，一般情况下k远远小于m和n，进而达到降维的目的。Ui和Vj分别表示对应的用户ui和商品vj的潜在特征空间，通过UiTVj预测评分矩阵中的空值，进而得到预测评分矩阵。

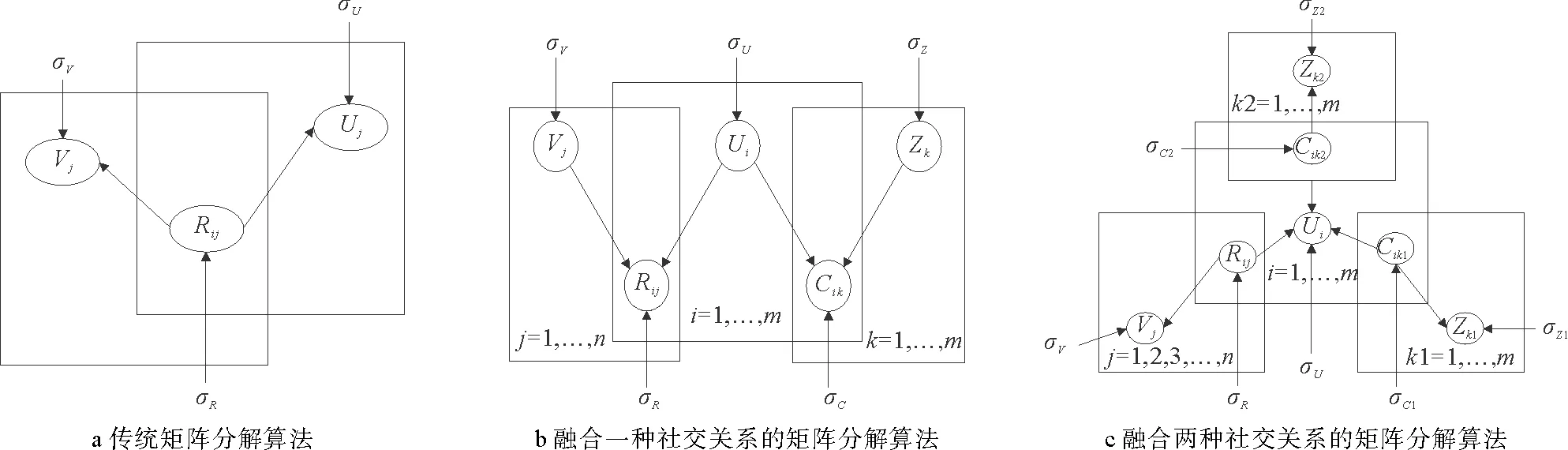
图3 推荐算法模型

为了方便研究，使用函数f(x)=1/Rmax,把用户对商品的评分映射到[0,1]区间，其中Rmax表示用户对商品的最大评分。传统的矩阵分解只是利用了简单的线性模型R=UTV，得到的结果会过于拟合评分矩阵，导致预测评分过分偏离真实的数据，最终预测结果失真[18]。所以，本文引用logistic函数g(x)=1/(1+e-x)，使得在[0,1]范围内界定用户对商品的评分，所以观测得到的条件概率分布可定义为

(1)

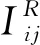
(2)

(3)

然后经过贝叶斯推理可得到U与V联合的后验概率分布:

(4)

2 融合社交关系的矩阵分解推荐算法

传统的推荐算法中用户之间是相互独立的，这忽略了用户之间的社交关系。在现实世界中，如果两个用户之间存在社交关系，则用户之间的喜好以及对商品的选择是会相互影响的，单纯考虑用户对商品的评分已经无法满足推荐的需求。因此这就需要将社交关系融入到推荐系统，进而提高推荐的准确率。

2.1 融合一种社交关系的矩阵分解推荐算法(MDRS1)

假设用户之间只有一种社交关系，通过共享用户的潜在特征空间将社交关系融入到矩阵分解推荐算法中，即社交关系的用户潜在特征空间与用户评分矩阵中的用户潜在空间是相同的，然后通过概率矩阵分解进行分析。C=Cik表示一个m×m的社交关系矩阵，将社交网络分解成U∈Rl×m和Z∈Rl×m分别表示用户特征矩阵和社交特征矩阵，将观测到的社交关系的条件分布定义为：

(5)

假设用户特征向量U和社交特征向量Z服从均值为0的球形高斯先验分布：

(6)

(7)

然后通过简单的贝叶斯推理，就可以得到：

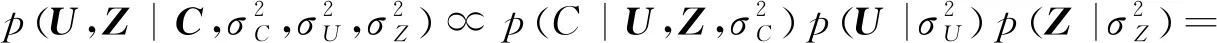
(8)

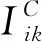
将一种社交关系融入到矩阵分解推荐系统，算法模型如图3b所示，同时分解用户商品评分矩阵和社交关系矩阵，得到一个潜在的用户特征空间，根据共享用户特征空间，将用户商品评分矩阵与社交关系矩阵紧凑联系，社会推荐的后验分布取对数可得：

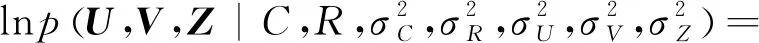
(9)

其中，C是一个不依赖于参数的常数，最大化的后验分布函数等价于最小化的目标函数，目标函数为

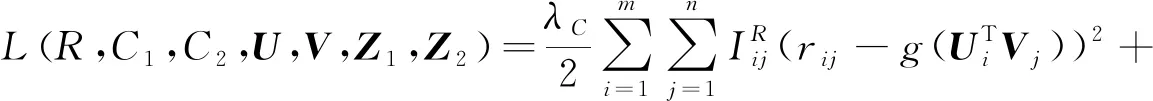
(10)

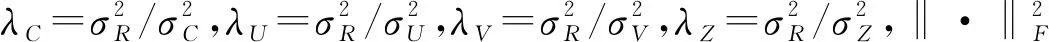
2.2 融合多种社交关系的矩阵分解推荐算法(MDRS2)

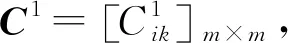
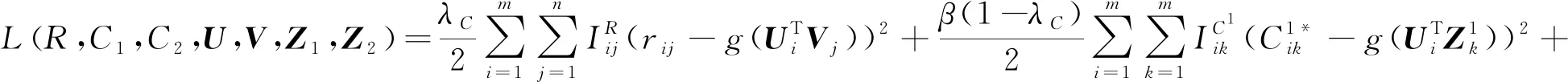
(11)

采用梯度下降算法对目标函数进行求解：

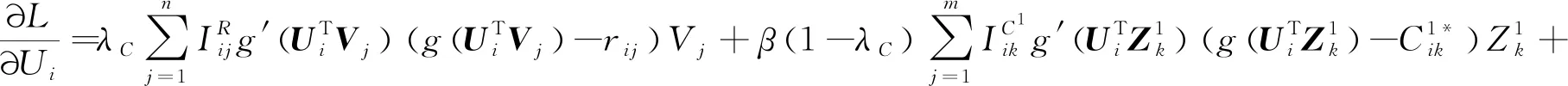
(12)

(13)

(14)

(15)

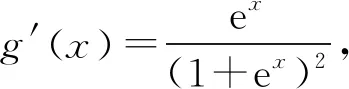
3 实验结果与分析

3.1 实验数据集

本文采用Epinions作为实验数据集，Epinions是一个知识共享网站和评论网站，用户可以评论商品或者给出从1到5的整数评级。新用户可以根据这些评论或者评级来判定商品是否值得购买或者电影是否值得观看。Epinions包括用户的信任关系，用户对商品的打分信息以及评论信息。Epinions数据集由49 290个用户组成，包括139 738个不同的项目，664 824条评论信息，487 181条信任关系。

在实验过程中采用五折交叉验证方法，对推荐模型进行训练与测试。将Epinions数据集平均分成五等份，每次实验中，随机选取一组作为测试集，其余四组作为训练集。进行5次实验，确保每组测试集都被测试。实验的最终结果为5次实验的平均值。

3.2 评级指标

本文采用三个不同的评价指标衡量推荐的准确性，分别为平均绝对值误差(Mean Absolute Error, MAE)、均方根误差(Root Mean Squared Error, RMSE)[19]和标准平均绝对误差(Normalized Mean Absolute Error，NMAE)[20]。这3种评价指标通过计算预测评分与真实评分之间的误差来衡量推荐算法的准确度，它们的值越小，表示推荐的准确性越高。MAE、RMSE和NMAE的定义分别如式(16)～(18)。

(16)

(17)

(18)

其中,rij是用户i对商品的j的真实评分，r′ij是用户ui对商品j的预测评分，EP表示测试集，rmax和rmin分别表示用户评分区间的最大值和最小值。

3.3 实验结果分析

在实验过程中，算法用户特征个数K=5，迭代次数为1 000次，λU=λV=0.001。参数α用于调节社交关系矩阵和用户评分矩阵之间的比重，参数β用于调节两种社交关系之间的所占比重，α、β的不同取值将直接影响推荐的结果。采用仿真实验的方法确定α和β的取值。β=1时表示只引入了一种社交关系，当α取不同的值时，其中MAE的值在数据集上的变化如图4所示。

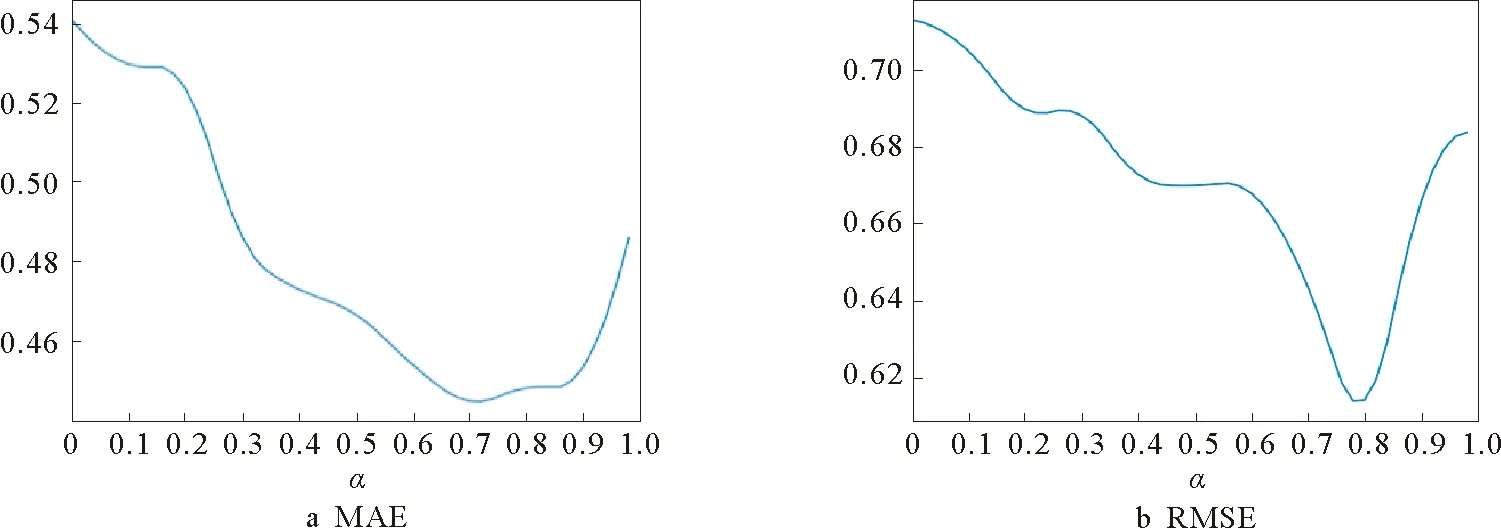
图4 参数α的影响

由图4可知，在Epinions数据集中，当α=0.8时，MAE和RMSE取值最小，即在只有一种社交关系的时候，α=0.8时推荐准确率最高。

用Ou、Ov分别表示用户u和v评价过的商品集，用户u和v共同评分的商品越多，那么表明他们可能有相同的兴趣并且彼此相互影响，具体定义如式(19)：

(19)

当fuv>0.2，代表用户u和v兴趣相似，设满足这个条件的用户之间的关系为c2关系。继续加载c2关系。当α、β取不同的值时，在Epinions数据集上MAE和RMSE的变化如图5所示。

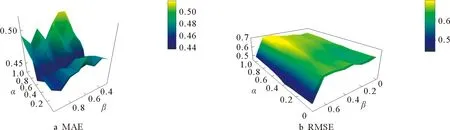
图5 参数α、β的影响

由图5可知，在Epinions数据集中，当参数α=0.3，β=0.4时，MAE的值最小，即在该算法中的推荐准确率最高，同理，当α=0.7，β=0.5时，RMSE的值最小，即在该算法中的推荐准确率最高。

为了验证本文所提的算法MDRS2的性能以及多种社交关系对推荐的影响，本文将MDRS2算法与SocRec算法[14](Social Recommendation Using Probabilistic Matrix Factorization，SocRec)，TDSRec算法[19](Similarity Social Recommendation with Trust and Distrust Information)和MDRS1算法在Epinions数据集上进行比较。SocRec算法在矩阵分解的基础上考虑了用户之间的社会关系属性，融入了一种社交关系；TDSRec算法在考虑社交网络的同时，融合基于用户评分偏好的相似性，共同对用户评分矩阵中的数值进行了预测；MDRS1算法仅考虑了一种社交关系；MDRS2算法通过共享用户特征空间，将用户商品评分矩阵与社交关系矩阵紧凑联系，将多种社交关系融入到矩阵分解中。实验统计结果如表1所示。

表1 不同算法的实验结果

由表1可知，在Epinions数据集中，本文提出的算法MDRS2的MAE、RMSE和NMAE的值相比其他方法的MAE、RMSE和NMAE的值要小，即预测的准确性较高。由此可见，引入两种社交关系的推荐算法比其他三种推荐算法的准确率要高，表明在推荐算法中，引入用户之间的多种关系将提高推荐的准确率，并且用户之间的关系越多，推荐的准确率越高。

4 结论

本文通过分解用户商品评分矩阵，根据多子网复合复杂网络，利用共享用户的潜在特征空间将多种社交关系融入到矩阵分解推荐算法中。通过在真实数据集上的实验证明了本文所提的融合多关系的矩阵分解推荐算法提高了推荐的准确率。说明引入多种社交关系可以更好地为用户做个性化推荐，并且引入的关系越多，推荐的效果越好。在今后的研究中，可以将用户的间接关系与直接关系相结合，来进一步研究社交关系对推荐的影响。