城市排水管网局部优化控制策略研究

宋雷震,何晓文

(淮南联合大学 智能制造学院，安徽 淮南 232001)

0 引 言

排水管网改建是城市排水系统工程的重要环节。当前我国排水管网系统仍主要以人工管理为主，不仅制约了管理的效率，且无法有效预防突发事件，因此，构建信息化的城市排水管网系统，全面提升管理水平尤为关键[1]。粒子群算法具有计算效率高且全局寻优能力强的优势，能够有效优化人工管理管网的局限性。在改建城市排水管网系统中发挥着举足轻重的作用。结合混沌粒子群算法的遍历性与随机性特点，常规粒子群算法进行优化改进，以实现改建城市排水管网，并达到排水管网信息化和现代化的目的[2]。

1 改进型混沌粒子群算法的管网优化

1.1 常见粒子群算法及流程

随机进化算法的粒子群算法(Particle swarm optimization，PSO)，主要优势体现在具备全局寻优能力，但PSO算法进化后期收敛速度慢，容易陷入局部最优的状况，且计算精度不高。因此，寻求PSO算法的改进优化策略，成为研究的重心[3-4]。混沌粒子群算法(Chaos particle swarm optimization algorithm，CPSO)借助自身的遍历性与规律性，能够有效避免PSO算法的局限性与不稳定性。然而，CPSO算法面对离散粒子群，即当混沌变量为固定值时，该算法难于适应离散状况[5]。此次研究分析并改进了CPSO算法，具体策略分别为加入混沌启动机制、历史记忆机制、以及对混沌变量μ进行改进，达缩短算法收敛时间，以及提升全局寻优能力的目的。标准粒子群算法：

(1)

其中：ω为惯性系数；r1和r2为随机数；0～1为随机数的取值范围；c1和c2为种群的学习因子；Vi为粒子飞行速度，Xi为粒子当前速度。对于PSO算法，本质在于通过粒子之间的相互关系进行寻优计算。在每次迭代中，个体最优记为pb，表示每个粒子个体搜索到的最好位置；全局最优记为gb，表示N个粒子搜索到的最好位置[6]。PSO算法的运算过程就是粒子的位置和速度更新的过程。粒子在进行速度和位置计算时，根据全局最优、个体最优、及粒子的当前速度，调整粒子的飞行速度和方向，当迭代次数为期望值时，结束运算，最优解为最后迭代的全局最优值。混沌粒子群算法原理及流程见图1。由图1(a)可见，常规粒子群算法优势与局限同样明显。由图1(b)可见，结合混沌运动的遍历性与随机性，在混沌序列的适应度值中确定最优粒子，可克服粒子早熟问题[7]，有效提高了收敛速度，提高了计算精度和搜索效率。CPSO算法：

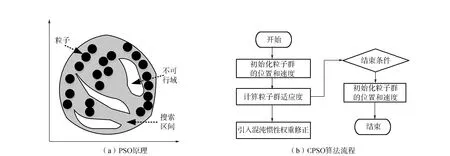
图1 混沌粒子群算法原理及流程Fig.1 Principle and flow of chaotic particle swarm optimization

(2)

其中：μ为混沌控制参量，gb为全局最优，pbi为种群个体最优，Xman和Xmin分别为粒子取值范围的上限值和下限值。在混沌粒子群算法中，当任意初始值Z0和控制参量μ给定，经过迭代，得出确定的时间序列。当最大迭代次数满足期望值时，运算结束，否则重新计算适应度值。混沌作用见图2。由图2可见，当混沌参量μ=4且满足实践序列z取值在[0，1]时可达到最大混沌状态。混沌系统具备随机性与遍历性，该算法具备全局寻优特点。混沌粒子群算法的具体步骤：①初始化，涉及内容部包括混沌寻优次数(MaxC)、进化次数(Tmax)；②进行粒子群迭代；③计算适应度值。

图2 混沌作用Fig.2 Chaos

1.2 改进型混沌粒子群算法

引入混沌(Chaos)思想，构建混沌粒子群算法，可以完成PSO算法后期搜索不稳定的状况[8]。研究分析并改进了CPSO算法，提出了改进型混沌粒子群算法(HMCPSO)，具体策略分别为加入混沌启动机制、历史记忆机制、以及对混沌变量μ进行改进，以到达缩短算法收敛时间，以及提升全局寻优能力的目的。加入混沌启动机制描述详见式(3)。

(3)

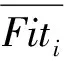
(4)

当δ2=0时，需要进行混沌运算，即此时粒子群可能陷入局部极值。由于引入历史记忆机制，保留了较好的适应度值粒子，保证了寻优过程中的粒子始终是历史最优粒子。式(3)中的k值，可以根据迭代次数以及具体模型进行确定[10]。在对混沌变量进行改进层面，当混沌变量值为4时，系统的混沌化最大。面对粒子离散状况，单纯进行混沌粒子群运算，导致后期粒子陷入局部极值状况，且混沌参量与混沌寻优次数固定时，经过离散化后的粒子最优适应度值下降，且无法跳出局部极值的局限。需要对混沌变量μ进行改进，改进策略描述

(5)

针对混沌算法在粒子离散状况下的局限性，对混沌参数μ进行改进。将μ设置为渐变参量，由于初始参量对于混沌运算具有显著影响，可设置混沌参量取值在[3.90～3.95，4]，并在具体迭代过程中，逐步加大混沌参数，以加强混沌运算，保证混沌运算的稳定性[11]。本研究分析并改进了CPSO算法，提出了HMCPSO算法。算法流程见图3。

图3 改进型混沌粒子群算法Fig.3 Improved chaotic particle swarm optimization algorithm

由图3可见，研究对混沌粒子群进行改进，通过对加入混沌启动策略，历史记忆策略和混沌变量μ的重新设置可将算法的收敛时间缩短，提升全局寻优能力。粒子群算法具有计算效率高且全局寻优能力强的优势，能够优化人工管理管网的局限性。因此，在改建城市排水管网系统中发挥着举足轻重的作用。同时，结合混沌粒子群算法的遍历性与随机性特点，常规粒子群算法进行优化改进，以实现改建城市排水管网，并达到排水管网信息化和现代化的目的。

2 排水管网局部优化控制结果分析

2.1 改进算法性能分析

排水管网双环模型在HMCPSO算法中，通过引入历史记忆机制，并在其他初始条件保持不变的情况下，赋值k=3时，对比分析了HMCPSO算法与PSO算法性能。同时，在将HMCPSO算法具体应用到排水管网模型中，通过改进混沌变量μ，保持其他初始条件不变，对比分析HMCPSO算法与PSO算法性能，结果见图4。

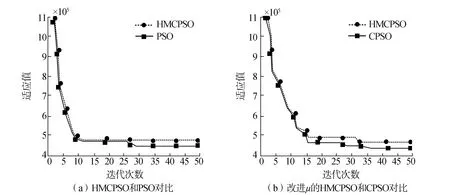
图4 改进算法性能结果Fig.4 Performance results of improved algorithm

由图4(a)可见，粒子在迭代过程中，位置不变，且寻优粒子，始终是历史最优粒子，并通过启动混沌机制，保证种群进行全局寻优。表明引入历史记忆机制能够有效地克服PSO算法局限。由图4(b)可见，完成对混沌变量μ的改进之后，促进了种群的寻优速度，继而克服了CPSO难以跳出局部最优的局限。

2.2 改进粒子群算法优化排水管网实验分析

实验选取城市排水系统简化后的Hanoi管网模型，其管道布局结构，以及不同管径在单位管长的情况下所对应的耗能值见图5。由图5(a)可见，管道布局共有32个节点，且每个节点对应者管道的长度与管径。其中，32个管道的管径分别为762、508、304.8、406.4、609.6、1 016 mm，管长为100～3 500 m，二者共同构成了Hanoi管网模型。由图5(b)可见，单位管长下管径为762、508、304.8、406.4、609.6、1 016 mm的能耗值分别为181.81、98.38、45.73、70.14、129.34、278.31美元，由此可见单位管长下管径为304.8 mm时能耗最少。

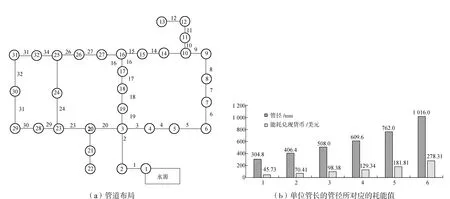
图5 不同管径在单位管长的能耗值Fig.5 Energy consumption of different pipe diameters per pipe length

为了验证以上改进算法应用于排水管网排水优化调度的效果，对算法进行了仿真实验。其中，两种算法在不同算法参数设置下的实验对比结果，见图6。由图6(a)可见，1、2、3、5、9、10是标准粒子群算法的调度结果，1、4、5、6、7、10是改进粒子群算法的调度结果，两种算法均经历了6个节点。虽然节点数相同，但由图6(b)可见，在相同能耗值的情况下，改进算法的评价次数为29 600，远小于标准算法的65 200，且改进算法的成功率为94%，也高于标准算法的92%。简言之，改进的粒子群算法计算代价更小，成功率更高。

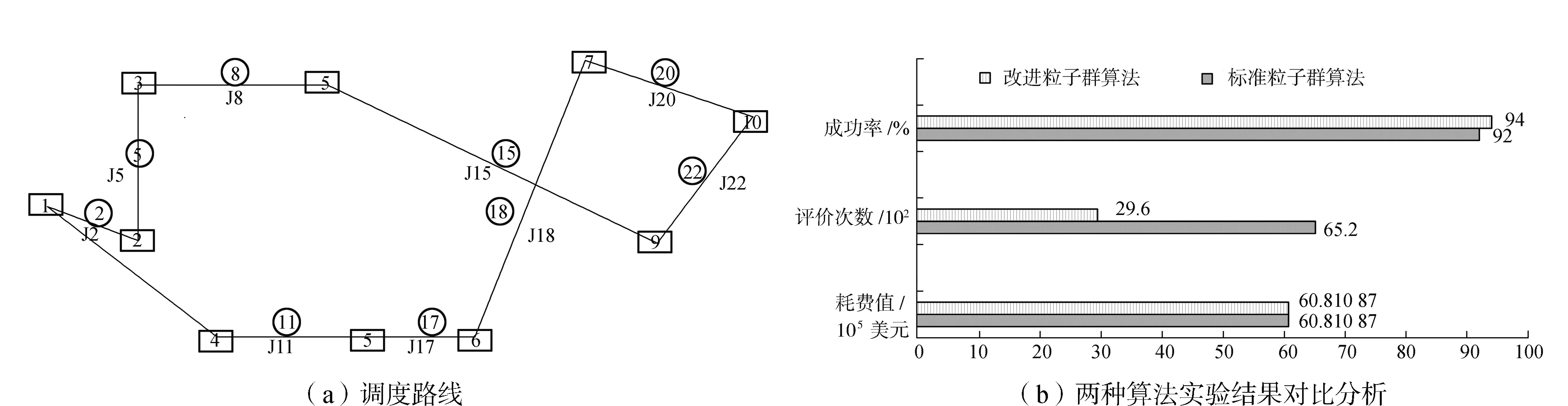
图6 两种算法对排水管网调度结果Fig.6 Scheduling results of drainage network by two algorithms

3 结 论

粒子群算法具有计算效率高且全局寻优能力强的优势，能够有效优化人工管理管网系统的局限性。研究结果表明，HMCPSO算法量最优为2.2×106元，且方差为2.422 3×1010元2，以及均值为2.885×106元，小于其他两种粒子群算法，继而保证了粒子种群全局寻优的能力；且收敛时间为12.68 s，搜索率为98.6%，不仅缩短了算法运行时间，而且提高了算法运行的稳定性。改进型混沌粒子群算法，克服了CPSO 算法的局限，相对于CPSO算法更稳定，既保证了粒子种群全局寻优的能力，又缩短了算法运行时间，实现了城市排水管网局部优化控制。