A comparison of transient reflection and transmission techniques for electron and lattice dynamics in metal nanofilms

WU Wen-Zhi, REN Shi-Wei, KONG De-Gui, CHAI Zhi-Jun

(College of Electronic Engineering, Heilongjiang University, Harbin 150080, China)

Abstract：The electron and lattice dynamics of gold and copper nanofilms are measured with femtosecond transient reflection and transmission techniques. Two-temperature model (TTM) and Crude-model approximation are applied to study the mechanism of heat transfer for metal nanofilms theoretically. Electron and lattice temperatures are calculated by TTM, which assume electron-lattice coupling coefficient as a constant for gold and copper. Compared the results of reflection with transmission, the difference of electron relaxation is negligible at the first two picoseconds, but electron-lattice coupling effect in the transmission method is stronger and more sensitive than that of the reflection method under the identical experimental conditions. Change of temperature gradient along with the direction of film thickness and electron-lattice coupling resistance due to the boundary scattering are responsible for the difference between transient reflection and transmission data. Both transient reflection and transmission of semitransparent films should be considered together for the investigation on the mechanism of ultrafast dynamics.

Key words：two-temperature model (TTM); electron-lattice coupling; ultrafast pulsed laser heating; substrate effect; Crude-model approximation

Some ultrathin semiconductor and metal nanofilms are semitransparent at the range of UV-Visible and near infrared wavelength, the steady and excited-state absorption spectra of them can be obtained after the combination with reflection and transmission spectra[1]. Optical transmission is the characteristics of a semitransparent sample to permit the passage of light, with the incident light being absorbed partly. In the past twenty years, semitransparent metal[2-4]or semiconductor nanofilms[5]is applied extensively in photoelectric devices for their excellent photoelectric and thermal properties, and these properties of semiconductor nanofilms take an important role in determining the heat dissipation and response capability of micro-structure devices. With the development of molecular beam epitaxy and magnetron sputtering techniques, semiconductor, and metal nanofilms can be prepared with high smoothness. Relaxation mechanism on free carriers between the electron-electron[6]and electron-lattice[7-8]remains a hot topic of solid-state physics. In semiconductor or metal thin films, the time-resolved measurements of the ultrafast dynamics show important temperature dependence on the electron-lattice coupling, which in the nonequilibrium transient heat transfer process of the highly excited electron-lattice system[9]. Due to the high density of electrons in metals, the initial stages of electron relaxation are connected with electron-electron interactions and their electronic effects, which can be illuminated by relatively simple models[10].

Extensive investigations on the ultrafast dynamics of gold[11]and copper films[12]have been conducted previously. Hopkins and Norris[13]studied in the nonequilibrium heat transfer of Au film, the substrate of the gold film is effected by the electron-lattice coupling, it must exist the energy loss and transferred from the electron system to the metal lattice. The 5 nm thick gold film on BK7 substrate as a sample, and the ultrafast electron dynamics of it have been investigated as a function of film morphology, through the transient reflectivity measurements results, a sub-100 fs rise time and a complex relaxation profile on picosecond timescale can be observed[14]. Guo， et al.[15]investigated the interfaces heat transfer between metal and dielectric after the ultrafast-laser acting by transient reflection technique. The temperature nonequilibrium between electrons and lattices exist in gold film obviously after utilizing ultrafast-laser heating, transient thermo-reflectance measurement using femtosecond laser pulses on Au-Si samples and the simulation based on a two-temperature model are compared with the measured data. The results illustrate the direct coupling between electrons in metal and lattice in dielectric is strong when the contact resistance is sufficiently small. A molecular dynamics method based on TTM for predicting and numerical modeling the thermal resistance between metal and nonmetal interface[16]. The effective nonlinear optical absorption coefficient is measured for 20-nm-thick Au films as a function of pulse width by use of Z-scan measurement. Differential transmissivity and reflectivity measurements are performed at 775 nm pump and 630 nm probe pulses. By simulating the experiments which based on TTM and the analysis results of electrons and lattice can be obtained[17]. However, the detailed interaction mechanism between film and substrate is still in debate. Comparison between transmission and reflection experiments of metal nanofilms based on the change of dielectric function can provide abundant information to understand substrate effect of metal nanofilms.

Two typical metal nanofilms and measure the ultrafast dynamics using transient reflection and transmission technique is choosed under the same experimental conditions, respectively. TTM is used to simulate the temperature of electron and lattice at the surface of nanofilms. Time dependence on electron and lattice temperatures shows an obvious deviation between transient reflection and transmission results. Crude-model approximation is used to explain the noticeable difference of dynamic profiles between transient reflectivity and transmissivity measurements. Fitting of experimental data shows combining the results of predicted lifetimes with the observation are reasonably close, and the time dependence of the relaxation rate cannot be neglected when analyzing a systematic deviation between transient reflectivity and transmissivity measurements. Considering interface thermal resistance and gradient change of temperature along with the direction of film thickness, transient reflectivity and transmissivity can be derived, and the equilibrium state of both electrons and lattice could be affected by the substrate.

1 Experimental section

1.1 Gold and copper nanofilms preparation and characterization

BK7 glass substrates with the thickness of 170 μm are purchased from Agar Scientific Ltd. The substrates are first cleaned with acetone, ethanol then soaked in a detergent solution, and finally rinsed with de-ionized water and dried with nitrogen. Gold and copper nanofilms are fabricated by electron-beam evaporation deposition technique[18], which is the most consistent method. The gold film (60.0 nm) and Cu film (57.5 nm) are prepared by evaporating 99.999% pure gold and copper onto the substrates respectively. The thickness of metal nanofilms is measured by use of atomic force microscope (Nanosurf-Easyscan). The substrates are not intentionally heated by pump laser pulse. The evaporation rates and the thicknesses are monitored by an IC/5 thin film deposition controller (INFICON) with a 6 MHz Au-coated crystal[19]. For gold nanofilm, the obvious absorption peak locates at 510 nm, and the thickness of 60 nm can be evaluated as shown in Fig.1(a). All the measurements are performed quickly after the evaporation of thin film in order to decrease the oxidation of thin film.

1.2 Experimental section

The home-built transient reflection/transmission setup is demonstrated as shown in Fig.1(b).The source of ultrashort laser pulses consists of a mode-locked Ti: sapphire regenerative amplifier oscillator generating 120 fs pulses at the wavelength of 800 nm (Coherent, Legend), with pulse energy close to 1 mJ at a repetition rate of 1 kHz. The ultrafast pulses are used in collinear pump-probe geometry, where the beams are frequency doubled at 400 nm using a nonlinear beta-barium borate (BBO) crystal. The collinear pump and probe pulses are focused onto the sample surface to a spot size of 100 μm and 80 μm respectively. The radii of the pump and probe beams are measured with a sweeping knife edge method. The reflection and transmission data collected with a photo detector is locked into the pump modulation frequency to get the induced reflectivity ΔR/Rand transmissivity ΔT/Tat the same wavelength using a time-delayed probe pulse. Though 400 nm excitation light penetrates depth of gold and copper are 16 nm and 13 nm respectively, nanoscale gold film possess nonlinear absorption after 400 nm femtosecond laser excitation through the focal lens[17]. So, the substrate and boundary effect should be considered in the process of energy transfer between electrons and surrounding material systems.

Fig.1 (a) Absorption spectrum of translucent gold film, insets are the morphology of cross section and surface of golf nanofilms with the thickness of 60.0 nm, respectively; (b) Schematic diagram of transient reflection and transmission experimental setup

2 Results and discussions

2.1 Two-temperature model and numerical analysis

TTM can be solved numerically to predict the time dependence of electron temperature and lattice temperature[20-24], which commonly describes the evolution of the temperature changes due to the absorption of a laser pulse within the solid in spatial and temporal domain. TTM has been applied to simulate the process of heat transfer in metal thin films by femtosecond laser pulses[25-26]. According to TTM, the evolution of electron temperature Te and lattice temperature TL can be expressed as:

g[TL(x,t)-Te(x,t)]+Q(x,t)

(1)

(2)

where the specific heat capacity of the electronCeis linearity with the electron temperature,CLrepresents the specific heat capacity of the lattice and electronic heat conductivityκe, which is expressed byκeTe/TLandκeis the equilibrium electron thermal conductivity measured at room temperature. Temperature dependence on metal films is shown to be inaccurate for electron temperature beyond 1×104K, but at the low pump fluence the electron-lattice coupling factor is a constant. Detailed parameters are listed in Table 1.

Table 1 TTM parameters for gold and copper nanofilms

The pump laser pulse is assumed to be Gaussian in shape with a pulse width of 0.2 ps. Eq.(1) and (2) can be numerically solved as shown in Fig.2, which shows depth dependence on the electron and lattice temperatures at a fixed value of the electron-lattice coupling constant. Because of the electron heat capacity is less than lattice heat capacity, electrons are heated to a high temperature in a short time. We can see that the temperature of electron rises rapidly within the range of 0～500 fs at the film surface (x=0), and the maximum temperature reaches 2 240 K. When an ultrafast laser pulse heats the electrons in the metal, and for a short time (<1 ps), the electrons are driven out of equilibrium with the host lattice because the lattice temperature cannot rise too high in a short time to maintain equilibrium. Consequently, the electron temperature rises far above that of the lattice. There occurs non-equilibrium thermal phenomenon of electron and lattice due to the presence of the temperature difference between the electron and the lattice. Subsequent to the excitation of the electrons which they transfer energy to the lattice through the lattice scattering, and the electron and lattice temperatures equilibrium is the rate limiting step by the strength of the electron-lattice interaction.

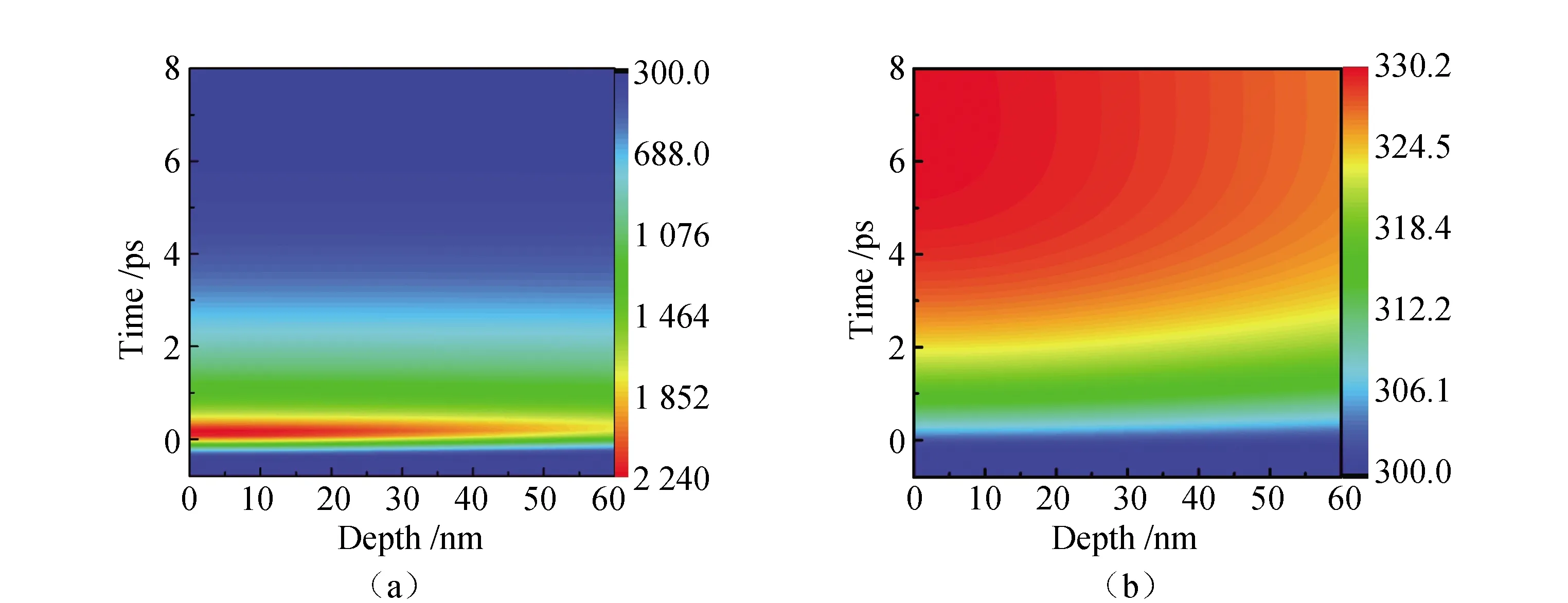
Fig.2 (a)Electron temperature gradient change of 60.0 nm thickness gold nanofilm relates to the time and the depth along with film thickness direction; (b)Lattice temperature of 60.0 nm thickness gold nanofilm connected with the depth along with the film thickness direction and the time.

In Eq.(1),Q(x,t) describes the absorbed energy, which has a Gaussian temporal and spatial shape alongtandxwith the film depth coordinate:

(3)

where the fluenceFand pulse widthtpare parameters of incident laser pulse, the reflectivityRand transmissivityTrelate to thickness and property of substrate material, the magnitude ofRis roughly eight times than that ofT, and d denotes film thickness. Moreover,xis the distance from the inside of the film to the surface, andtdenotes the time delay after the laser reaches the surface of the material. The reflectivityRand transmissivityTat normal incidence on plane-parallel surfaces absorbing film bounded by air and glass substrate which both are transparent and non-absorbing media are given[27]by,

(4)

T=

(5)

whereε=ε1+iε2is the dielectric function of the metal film,ε1andε2represent the real and imaginary parts of dielectric function respectively. In addition,εs=ε1s+iε2sis the dielectric function of BK7 glass substrate,εwhich is transparent for the 800 nm spectral region and thenε2s=0.α1is the absorption coefficient of the metal film. From the equation (5), we can see that the transmissivityTis related to the dielectric function of BK7 glass substrateεs. Three kinds of coupling exist at the interface which between the gold nanofilm and substrate as follows: The electron and lattice coupling within gold nanofilm, the electron in gold nanofilm coupling with the lattice in substrate, and the lattice in gold nanofilm coupling with the lattice in substrate, and the lattice-lattice coupling give rise to the resistance on the interface. The main reasons which causing the decrease of the temperature are the electron-lattice coupling and heat diffusion, which is due to the existence of temperature gradient that energy spreads by diffusion in two materials here. Moreover, the reason why there exists heat diffusion is the temperature difference between gold nanofilm and substrate, for BK7 is dielectric, there are no free electrons in it, when the electron-lattice coupling reaches equilibrium, the temperature in gold nanofilm is different with it on the substrate surface all the time, so a part of electrons which have reached the equilibrium coupling with lattice in substrate and the temperature decreased. The dielectric constants at specific wavelength are obtained from the database. The reflection and transmission change are related to the alteration of the dielectric functionε[28]as,

ΔR/R=(Δε1∂R/∂ε1+Δε2∂R/∂ε2)/R

(6)

ΔT/T=(Δε1∂T/∂ε1+Δε2∂T/∂ε2)/T

(7)

For a thin film, where ∂R/∂ε1, ∂R/∂ε2, ∂T/∂ε1, and ∂T/∂ε2can be derived by Eq.(4)-(5) respectively. Δε1and Δε2are the change of the real and imaginary part of dielectric function, which can be calculated by integrating all the available transitions from d-band to conduction band, located atLpoint of the band structure by Rosei’s dielectric function model[29].The difference between reflection and transmission can be discussed theoretically. For opaque film, the effect of substrate needed to be considered due to the change of refraction index.

2.2 Gold and copper nanofilms using TTM analysis

The lowest energy d-band to available Fermi level transition is small for gold (2.40 eV) and copper (2.15 eV), it’s necessary to consider the effects of interband and intraband transitions on the transient reflection and transmission due to the excitation photon energy of 3.1 eV[30]. When the excitation photon energy is larger than interband transition threshold, electrons in the d band can also absorb the energy and transit over Fermi energy. Here, the output at 800 nm (1.55 eV) from the laser which is below interband transition threshold, the excitation fluence is low enough to make the number of s/p band is much more than that of d-band electrons, under this condition the effect of the d band perturbation to the transient reflectance is ignorable[30].

Electron relaxation in metal exists at the first two picoseconds, the transmission and reflection results are similar at the first two picoseconds as reported, so inter- or intraband transition of electrons is not directly due to the pump pulses after the initial fast transient.

(8)

where e-(t/τ)2is the instrument response function, ΔTeand ΔTLare the variation of electron and lattice temperature, respectively. According to the literature[30], at early times after 150 fs laser excitation, the normalized reflectivity change ΔR/Ror the normalized transmission change ΔT/Tis proportional to the normalized temperature change of the electron gas and lattice, hence, the surface reflectivity kinetics is obtained and assigned to the surface temperature variations. But for ΔT/T, probe and pump pulses transmitted through the glass substrate, thermal diffusion and interface resistance should be considered. The classical TTM is hard to estimate the dynamics measured by transient transmission method. With decreasing film thickness to the order of the thermal penetration depth, the boundary effect is essential to be solved during the electron-lattice coupling equilibrium process. The effect of substrate is negligible for TTM. From TTM, the thickness dependence has been considered but substrate dependence has not been considered. Through modify electron-lattice constant to optimize the measured dynamics with least square errors from TTM fitting. The magnitude of ΔTis roughly three times higher than that of ΔR. Consequently, the total change in the absorption for the Au film is about three times than previously obtained from the analysis of the transmissivity.

At the stage of rise time and longer delay time, the experimental results are not satisfied with the simulation of TTM because of the limitation of time resolution of the setup, the coevolution is applied to fitting. The initial stage of eight picoseconds is discussed with the classical TTM, which is shown above in Fig.3. The agreement between the fitted results and the experimental data is generally favorable from zero to eight picoseconds. The small discrepancy between the experimental and the simulation results should stem from substrate effect and thermal diffusion. The change rate of gold film reflectivity is slower than the change rate of the copper film reflectivity. Firstly, because the electron-lattice coupling coefficient of gold is 2.3×1016Wm-3K-1, under the same laser energy density and film thickness condition, the electron-lattice coupling coefficient of copper is 1.0×1017Wm-3K-1, and the electron-lattice coupling coefficient is used to represent the energy transfer rate from electron to lattice. The larger the electron lattice coupling coefficient, the shorter time of the electron and the lattice to reach the same temperature, and the temperature change faster. Secondly, the thermal conductivity of copper is larger than that of gold at room temperature, the heat conductivity capability of copper is greater than that of gold, so the temperature of copper changes faster than that of gold.

Fig.3 (a) Time-dependent differential reflection curves for Au nanofilm pumped with pulses of 200 fs, 400 nm and energy from 50 to 110 nJ; (b) Time-dependent differential reflection curves for Cu nanofilms pumped with pulses of 200 fs, 400 nm pulse with pulse and energy from 50 to 110 nJ

2.3 Electron and lattice dynamics using Crude-model approximation

In order to investigate the influence of the data acquisition mode on ultrafast dynamics, we chose gold and copper semi-transparent metal nanofilms to measure the transient signal. For most semiconductor at high laser excitation, the local dielectric function is modified and creates a discontinuity at their surface. So, we can observe the change of the sign of transient reflectivity. However, for gold and copper thin film we measure the reflectivity and transmissivity signals using transient reflection and transmission technique at the same experimental conditions, the sign of transient transmission results varies with the delay time. Transient transmissivity is pushed down compared with transient reflectivity.

Since the change of the transmission, the reflection, and the absorption must sum to unity, the change in the total absorbance ΔAequals-(ΔT+ΔR).

(9)

whereI0is the intensity of incident laser pulse, ΔTand ΔRare the intensity of transmission and reflection under steady-state condition. For Au and Cu nanofilms the ratio of intensity between reflectivity and transmissivity is about 20 at steady-state measurement. Comparing the transient reflectivity changes with transient transmissivity changes shown in Fig.4, the time-resolved experiments reveal that both ΔTand ΔRare negative, leading to an increase of the absorption, but they are different for the profile of ultrafast dynamics. The transient reflectivity and transmission data of gold and copper nanofilms are presented for the case of incident laser pulse energy from 50 to 110 nJ. The Crude-model approximation which separates the electron-gas fluctuation into thermalized and non-thermalized components, and a further analysis of the transient reflectivity and transmissivity changes which can be observed[9]. In all cases the data show a sub-picosecond rise time and a picosecond timescale relaxation. These data are initially fit with the function[19, 20]as,

e-(t-t′)/τep+B(1-e-(t-t′)/τep)]e-(t′/τ)2dt′

(10)

whereτrrepresents the sub-picosecond rise time and it is related to the relaxation dynamics of the non-thermal initial distributions, which giving a general description of the build-up of the Fermi distribution temperature through energy transfer. Andτepreflects the electron-lattice relaxation time related to thermal equilibrium.τis the instrumental response function, the value is about 800 fs. The final rising component is introduced to reflect the long-lived offset[9, 31]. This function gives an adequate fit to the data with rise times of 0.8 ps and about 1.1 ps for gold and copper nanofilms, respectively. With the energy of pump laser pulse increasing, rise time and transient transmission data are comparable with that of transient reflection data. Although the energy dependence on the electron relaxation can be ignored in this phenomenological approach, it provides a simple and qualitative description of the electron dynamics. This model results are almost agreement with the experimental results without considering small discrepancies. A better fitting is achieved by adding an additional term, introducing a second component in the electron-lattice relaxation as shown in Fig.4. In all cases the data show a sub-picosecond rise time and a picosecond timescale relaxation. The influence of the thermal resistance of the glass substrate also reduces the temperature of the backside of the gold film. In the ultra-fast process testing of metallic semipermeable membrane materials, the measurement of transient transmission or reflection may bring about experimental deviation, and transient transmission and reflection signals should be measured at the same time. Transmission data of them is semblable by comparing the reflection data of Au and Cu nanofilm at the first ～2 ps time range, but after ～2 ps, the change of sign for transmission dynamics exists for Cu and Au nanofilms at various pump laser excitations. The electron-lattice interaction of Au (or Cu) and lattice-dielectric interaction between Au (or Cu) and glass should be attributed to the difference between ΔR/Rand ΔT/T. At first, the electron-lattice and lattice-dielectric interaction happens at ～2 ps after the pump laser excitation. With the pump laser excitation, the increment exterior and interior temperature of metal film is different, the influence of gradient temperature is dominant to ΔT/Tbecause of the penetration of the whole film. We can also get pump power dependence of rise time and electron-lattice relaxation time.

Fig.4 Transient reflectivity and transmission data and fitting for gold nanofilm (a) and copper nanofilm, (b) recorded with different energies of pump laser pulse (50, 70, 90, 110 nJ)

Under the nonequilibrium thermal condition, the electron-lattice coupling of metal-nonmetal interface cannot be ignored for transient transmission. The higher the temperature is, the larger the electron-lattice coupling resistance[32]. From Fig.2(a), we can see that the highest electron temperature is 2 240 K, therefore, the electron-lattice coupling resistance is also large. Considering the electron-lattice coupling resistance, the total thermal conductivityκdecreases and the relaxation time of electron-latticeτepincreases, so with the laser energy density becomes higher, the recovery time to equilibrium is longer. Compared with the unexcited initial state, the total thermal conductivity of the electron-lattice system decreases and overcomes the larger electron-lattice coupling resistance, the temperature is lower than the initial state.

The combination between transient reflectivity and transmissivity for Au and Cu nanofilms are fitted using Crude model as shown in Fig.5.As the size of the devices drops to microscale and nanoscale, the role of Au-glass interface becomes increasingly important in determining the thermal and electrical performance. Electron-lattice nonequilibrium near the interface leads to lattice generation, which can disturb the original lattice scattering, and hence affects lattice transport, we would also consider the penetration of electrons into the nonmetal side. Reflectivity is a function of the surface, and transmission is a function affected by the interface, so we can see that transmissivity is more susceptible to the substrate than reflectivity. A linear increasing from time zero to rough 2.5 picoseconds, then keeping a constant of 0.3 for gold nanofilm and 0.4 for copper nanofilm. At first two picoseconds we can see no obvious change of relaxation rate between the transient and transmission signals because the effect of electron-lattice coupling exists. However, after two picoseconds, lattice thermal diffusion and interface thermal resistance should be considered, in addition, an account of the interaction process might be associated with interface thermal resistance and has a relaxation time with tens of picoseconds[33].

Fig.5 Combination between transient reflectivity and transmissivity for Au (a) and Cu (b) nanofilms at the same experimental conditions

The rising time and electron-lattice relaxation time of gold and copper nanofilms are shown in Fig.6. Because of the thicknesses is on the order of the thermal penetration depth, the result of transient reflection and transmission measurements are influenced by nonequilibrium between the electrons in the metal films and the lattices at the boundary of metal and substrate, and this phenomenon caused by electron energy loss to both the lattices in the metal film and those in the underlying substrate. Using Crude-model the electron-lattice coupling factor can be obtained and the excess energy loss from the electron system is observed for ～60 nm gold and copper nanofilms on glass substrates[9, 14]. With the pump pulse energy increasing, electron-lattice relaxation time of gold and copper nanofilms have a weak increment. Non-thermal rise time of transient transmission result is shorter than that of transient reflection result under the same experimental conditions. Lattice thermal diffusion and interface thermal resistance should be considered because the interaction process might be associated with interface thermal resistance and has a relaxation time with tens of picoseconds[34].

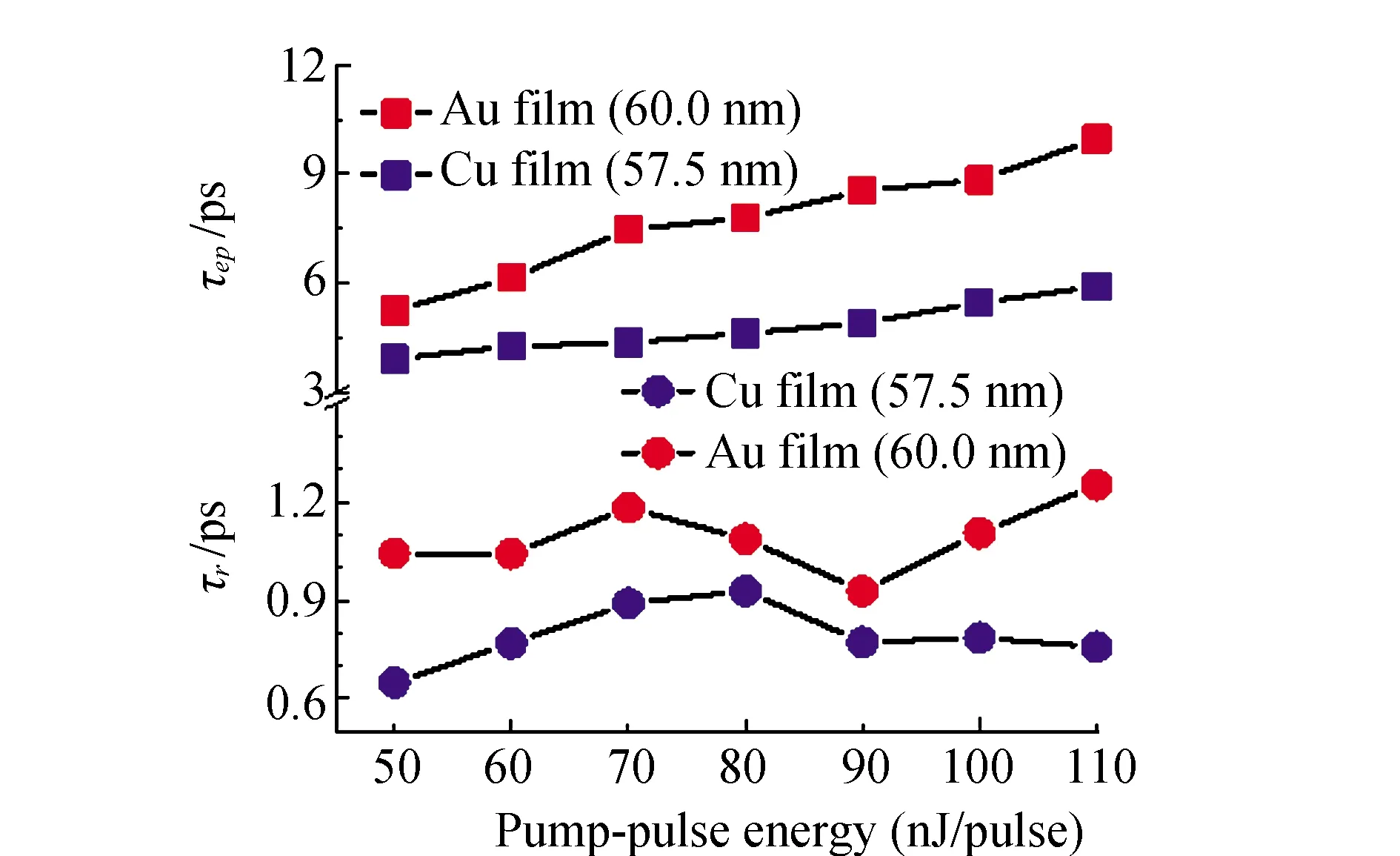
Fig.6 Rise time and electron-lattice relaxation time under various pump laser excitation based on therecombination between transient reflectivity and transmissivity for Au and Cu nanofilms

In the high temperature limit[13]:

(11)

where me is the effective mass, s is the speed of sound, ne is the electron density, andτis the relaxation time[35]. At high ultrafast laser excitation, electron-lattice relaxation time is not a constant; Using the Debye speed of sound,s=2.65×103ms-1for Cu ands=1.40×103ms-1for Au are calculated. From Eq.(11) we can plot the relationship between pump pulse energy and electron-lattice relaxation time. Energy transfer mechanism of opaque nanofilms during thermal nonequilibrium states between electrons and the surrounding material systems has a significant application to semiconductor devices[16].

3 Conclusions and perspectives

In summary, we investigate the ultrafast electron and lattice dynamics in nanofilms of gold and copper deposited on a glass substrate using transient reflectivity and transmissivity method. The experimental data are further analyzed in terms of TTM and Crude-model approximation which accounts for the relaxation of the initial optically excited and electron-lattice interaction, and we show the reason why the sign for transmission changes by analyzing the substrate effect. From these experimental and fitting results, the sub-picosecond relaxation of the optically excited electrons shows a relatively weak dependence on pump pulse energy, while the electron-lattice relaxation time which governs the lifetime of the thermalized electrons depends on the pump pulse energy. Electron-lattice coupling effect in transmission method is stronger and more sensitive than that of reflection method under the same experimental conditions. Therefore, through the transient transmission results, the effect of substrate should be considered more in the view of electron-lattice coupling and interface thermal resistance. These conclusions are being useful for investigating relaxation process of opaque nanofilms further.