网格形式对大跨度体育馆整体稳定性影响分析

向本军，李方慧,*，张智博，张 杰，王 程，张裕己

(黑龙江大学 a.建筑工程学院;b.水利电力学院，哈尔滨 150080)

0 引 言

空间网格结构常用于大跨度体育场馆，其结构几何非线性程度高，结构设计由稳定性控制。稳定性分析是空间网格结构、尤其是单层空间网格结构设计中的关键问题。

近年来,大跨度场馆的稳定性研究成果丰硕。沈世钊[1]对2 800多例不同形式的空间网格结构做了仅考虑几何非线性的稳定全过程分析，揭示了空间网格稳定的基本特征，拟合出空间网格结构极限承载力计算公式。范峰等[2]、蔡健等[3]、郭海山等[4]、Fan F等[5]对凯威特型空间网格运用多种方法进行了稳定性分析，对其线性稳定性与非线性稳定性分析提供了方法与理论指导。田伟等[6]、刘齐齐[7]通过引入杆件初始缺陷的方法研究杆件失稳对空间网格结构整体稳定性的影响。在大跨度空间结构中，沈世钊[8]对成都双流机场候机楼屋面大跨度单层柱面空间网格进行整体稳定性分析。对不同形式的空间网格结构，沈世钊[9]揭示了不同类型空间网格结构稳定性能的基本特性。杨东溟等[10]利用ANSYS结构分析软件对3种单层球面空间网格的稳定性进行了理论研究。张智博等[11]结合工程实际，对3种不同的双层空间结构的整体稳定性进行了对比分析。目前，国内学者对空间网格结构研究集中在支承条件、矢跨比、刚度、阻尼地震作用对凯威特型及其衍生的空间结构的影响上。

本文基于某复杂大跨度体育场馆，研究凯威特型、施威德勒型以及联方型3种不同空间网格形式对该工程的经济性、静力特性和整体稳定性的影响，利用3D3S14.0软件在控制用钢量以及K值条件下分别对3种方案进行对比，为工程实践以及相关理论研究提供依据。

1 工程概况

选取大跨度体育场馆结构矢高41.6 m,长轴153.0 m,短轴143.6 m。该场馆造型复杂,中间为圆形穹顶结构,底部为不规则曲面形成的气泡状结构。根据文献[12-13],在设计过程中,考虑构件的自重荷载与结构的悬挂荷载,恒荷载取值2.0 kN·m-2、活荷载取值0.6 kN·m-2。结构抗震设防烈度为7度(0.15g),设计地震分组为第一组,场地类别为Ⅱ类,基本风压为0.55 kN·m-2(100年一遇),基本雪压为0.55 kN·m-2(100年一遇),合拢温度15 ℃,作用温度-24～33 ℃(升温30 ℃,降温30 ℃)。选用Q355B钢材,顶部穹顶杆件选用矩形截面钢管，结构重要性系数取1.0,应力比取0.8。

2 结构网格方案

根据上部空间网格形式的不同划分为凯威特型(图1(a))、施威德勒型(图1(b))和联方型(1(c))3种空间网格结构。凯威特型空间网格结构[14]由10根通长的径向杆把球面分成10个对称扇形曲面的网格形式，在每个扇形曲面内由径向杆系和斜向杆系将曲面划分为三角形网格，在扇形曲面内力分布均匀，适用于中大跨度的屋盖；施威德勒型空间网格结构[15]由呈梯形分布的径向构件、环向构件和斜杆组成，整体结构合理、整体刚度以及抵抗非对称荷载能力强；联方型空间网格结构[16]的网格呈菱形，由左右斜构件相互交叉组成，造型美观，具有良好的受力性能。3种空间网格的跨度均为62.1 m，矢高均为 6.5 m。3种结构中间均采用圆形穹顶结构，底部均为为不规则曲面形成的气泡状结构。基于这3种结构方案对其静力特性、经济性和整体稳定性等方面做对比分析，进行方案优选。

图1 3种空间网格形式主体结构Fig.1 Main body structure diagram of three spatial grid forms

3 位移及用钢量对比分析

为了说明杆件位移对结构稳定性的影响，对凯威特型、施威德勒型与联方型空间网格结构分别进行用钢量与K值的控制，控制用钢量为3 300～3 400 t，控制K值为11.4～11.8(表1)。基于两种变量控制，分别对凯威特型、施威德勒型、联方型空间网格结构的大跨度体育场馆进行位移对比分析。

表1 用钢量与K值控制Table 1 Steel consumption and K value control

3.1 位移对比分析

对凯威特型、施威德勒型与联方型空间网格结构的用钢量与K值分别进行控制，利用3D3S14.0计算分析得到用钢量相近条件下与K值相近条件下的位移云图(图2、图3)。

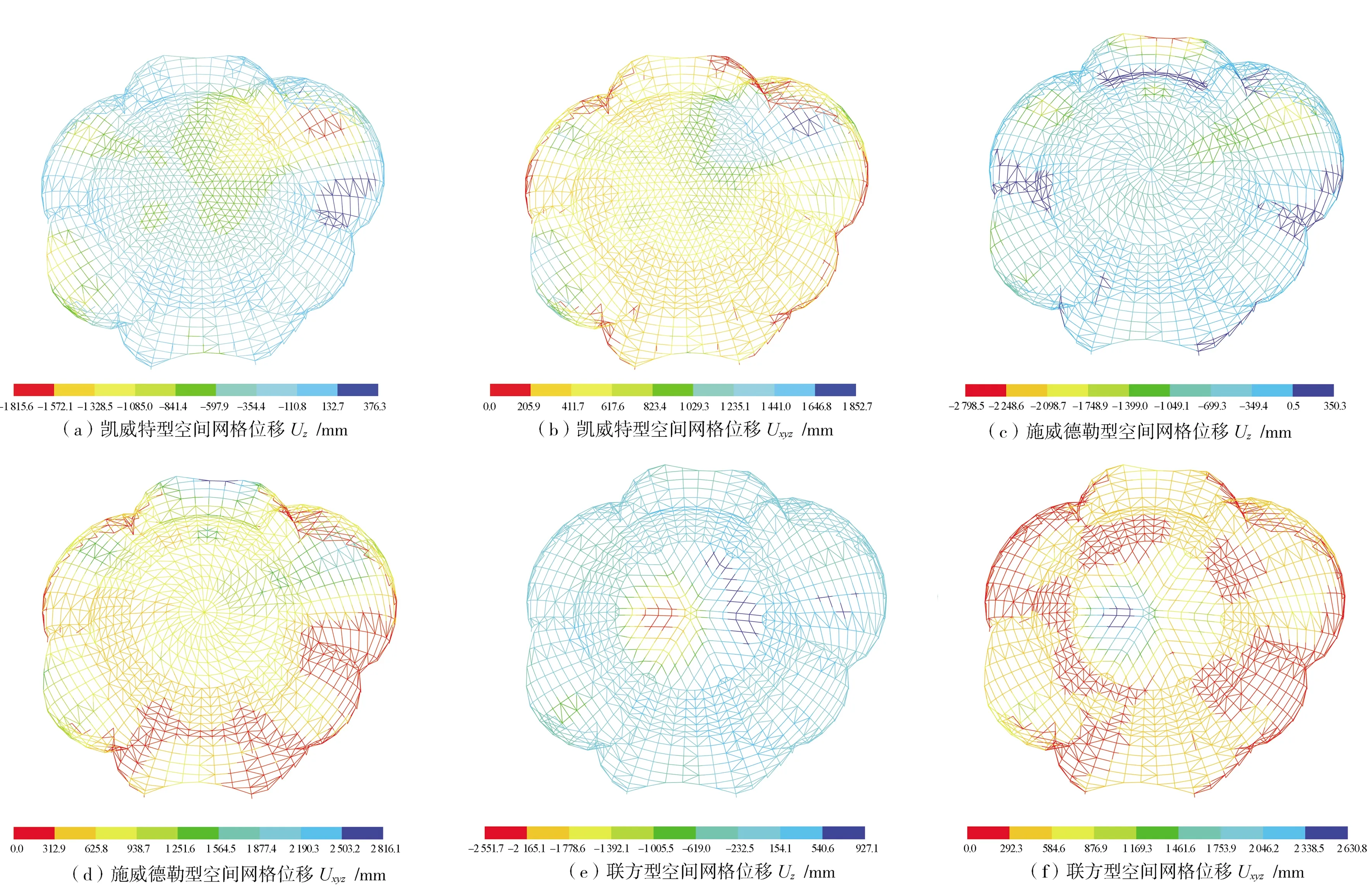
图2 用钢量相近条件下3个结构的位移Fig.2 Displacement of three structures with similar steel consumption注：正值表示杆件位移为z轴正向，负值表示杆件位移为z轴负向。

图3 K值相近条件下3个结构的位移Fig.3 Displacement of three structures with similar K value注：正值表示杆件位移为z轴正向，负值表示杆件位移为z轴负向。

本文采用空间直角坐标系：x代表横轴,y代表纵轴,z代表竖轴。通过对比分析可见，在用钢量相近条件下，凯威特型、施威德勒型与联方型空间网格结构的最大位移分别为1 852.67、2 816.12、2 630.83 mm；在K值相近条件下，凯威特型、施威德勒型与联方型空间网格结构的最大位移分别为2 126.13、2 188.12、2 299.51 mm。最大位移均以竖向位移为主，且最大位移均出现在底部气泡状网格结构上。可以通过提高空间网格结构的矢跨比、增设撑杆、增大底部气泡状结构的杆件截面面积来提升下部结构的刚度，达到控制结构竖向位移的目的。

3.2 用钢量对比分析

在K值相近条件下进行3种结构方案的用钢量对比分析，对结构所有杆件赋截面,并控制应力比为0.8。3个方案的顶部屋盖、中部结构与下部结构用钢量统计分析见表2。

由表2可见，在K值相近的条件下，在该大型复杂体育场馆工程中，3种方案的顶部屋盖的用钢量相差不大，但凯威特型空间网格结构的中部结构与下部结构用钢量要大于施威德勒型与联方型空间网格结构，这使凯威特型空间网格结构的下部结构刚性最好，因而最大位移最小。凯威特型与施威德勒型空间网格结构的用钢量分别为3 408.64、3 061.08 t，而联方型空间网格结构用钢量为2 608.67 t，说明联方型空间网格结构在工程实践中受力性能良好且工程经济效益高。

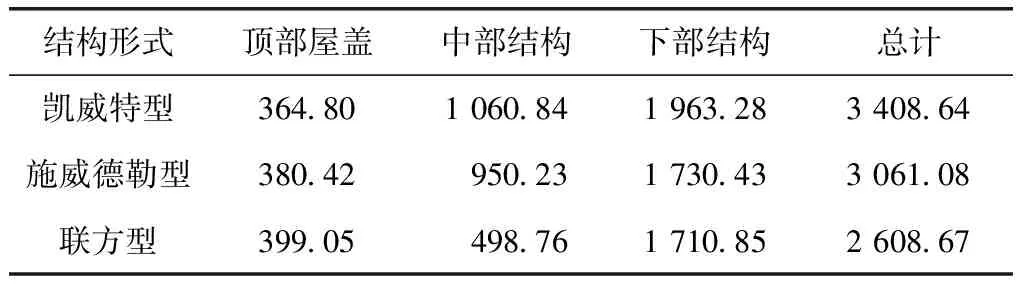
表2 用钢量统计分析Table 2 Statistical analysis of steel consumption t

4 整体稳定性分析

4.1 线性屈曲

通过3D3S14.0做特征值屈曲分析, 得到结构在恒载、活载、风荷载几种组合作用下前8阶线性屈曲稳定系数折线图(图4)。

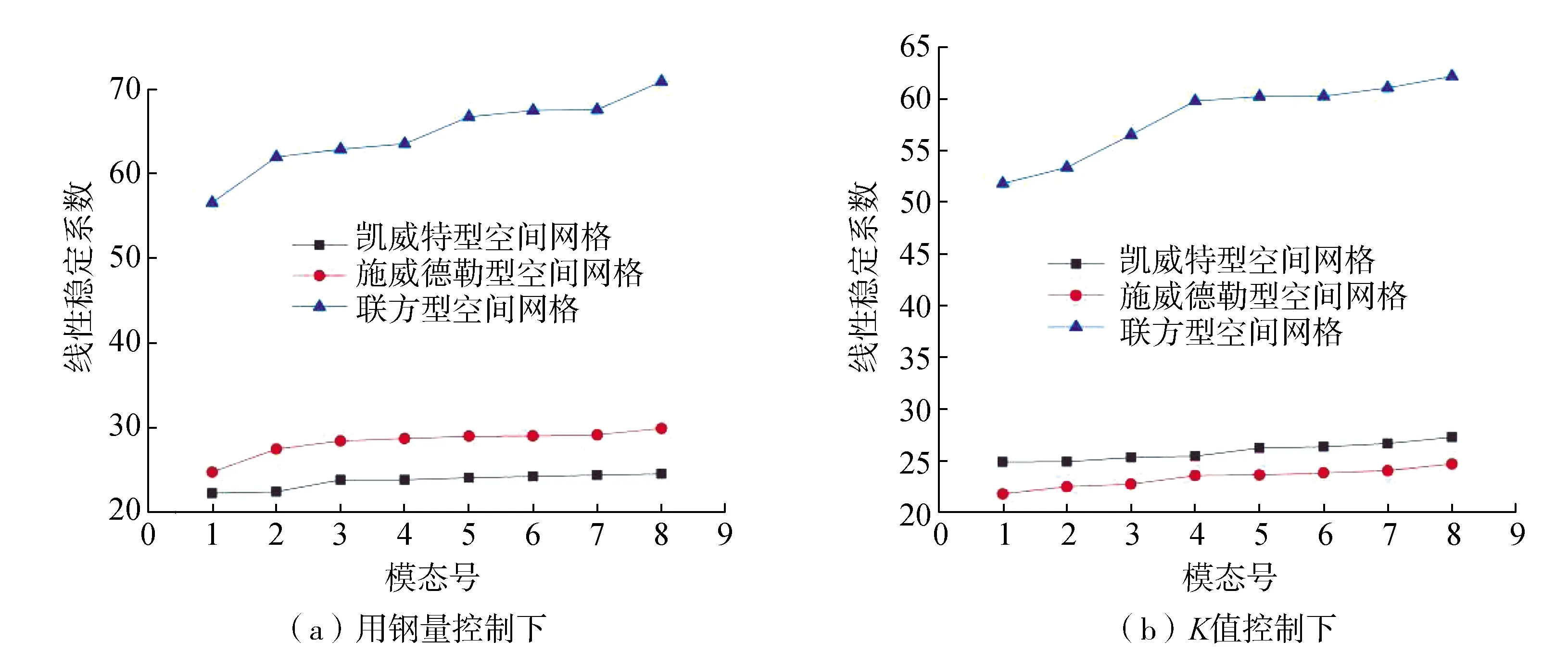
图4 线性稳定系数Fig.4 Linear stability coefficient diagram

分析3个方案前8阶线性稳定系数及屈曲模态。在该大型复杂体育场馆工程中，在用钢量接近的条件下凯威特型、施威德勒型与联方型空间网格的线性稳定系数最小值分别为22.24、24.76、56.57；在K值接近的条件下凯威特型、施威德勒型与联方型空间网格的线性稳定系数最小值分别为24.88、21.79、51.78。在所有模态中，均呈现联方型空间网格的线性稳定性要优于凯威特型与施威德勒型空间网格的特征。这说明联方型空间网格的网格形式对网壳的水平刚度与竖向刚度都有明显增强，使得联方型空间网格结构在受到多向荷载作用时最不易发生屈曲失稳。

4.2 非线性屈曲

采用空间网格规程[13]中所要求的空间网格短向跨度的1/300作为结构的初始几何缺陷, 引入分析模型,对空间网格进行非线性稳定分析，全过程分析得到的3种结构K值-Z向位移曲线(图5)。

图5 3个方案位移-K值关系曲线Fig.5 Displacement-K value relationship of three scenarios

由图5可见，在用钢量接近的条件下，该大型复杂体育场馆工程中，3种不同空间网格结构的K值分别为11.1、12.3、17.5，均满足规范中K>4.2的要求。3个方案中，联方型空间网格结构非线性稳定性最好。由于凯威特型与施威德勒型空间网格的刚度较小，受初始缺陷的影响较大，而联方型空间网格的刚度较大, 抵抗非对称荷载的能力较强，对初始缺陷的敏感性小。

5 结 论

通过对凯威特型、施威德勒型与联方型空间网格结构3个方案的经济性、静力特性和整体稳定性等方面对比，实现对复杂大跨度体育馆空间网格结构的优化设计，得出如下结论:

1)经济性方面，在该大型复杂体育场馆工程中，在控制K值相近条件下，联方网格型空间网格结构的用钢量为2 608.67 t，比施威德勒型少452.41 t，比凯威特型少799.97 t，说明联方型空间网格结构在工程实践中受力性能良好且工程经济效益高。

2)联方型空间网格在控制用钢量以及控制K值条件下的最大位移值分别为2 630.83、2 299.51 mm，在两种不同条件下均大于凯威特型网格，且位移以竖向位移为主。结构可通过提高空间网格结构的矢跨比、增设撑杆、增大底部气泡状结构的杆件截面面积,提升下部结构水平刚度,达到控制结构的竖向位移的目的。

3)联方型空间网格结构的线性稳定系数在控制用钢量以及控制K值条件下均至少两倍于凯威特型与施威德勒型，并且其K值分别是凯威特型与施威德勒型的1.58与1.42倍。这是由于联方型空间网格结构的刚度较大,受初始缺陷的影响相对较小，因此该结构的线性稳定性与非线性稳定性均优于凯威特型与施威德勒型空间网格结构。

4)对于该大跨度复杂体育场馆，联方型空间网格结构方案的最大位移在用钢量控制条件下比凯威特型空间网格结构大42%，比施威德勒型空间网格结构小7.04%;而在K值控制条件下，其最大位移比凯威特型与施威德勒型空间网格结构大8.15%与5.09%，均在可控范围内。但联方型空间网格结构造价分别比威特型与施威德勒型空间网格结构低23.49%与14.78%，且线性与非线性稳定性最好，因此为最佳网格方案。