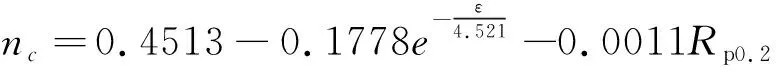汽车车身用Al-Mg-Si-Cu-Mn合金板材强度与n值的相关性研究
2021-12-28秦高梧
田 妮,刘 威,石 旭,赵 刚,秦高梧
(1.东北大学 材料科学与工程学院 材料各向异性与织构教育部重点实验室,辽宁 沈阳 110819;2. 东北大学 金属型线材研究中心,辽宁 沈阳 110819)

因此,本试验针对Al-0.67Mg-1.35Si-0.64Cu-0.61Mn合金冷轧板,通过热处理调控板材的微观组织结构差异仅是溶质原子的析出程度不同,并将析出的溶质原子控制成运动位错以切割机制通过的溶质原子团簇的基础上,通过回归分析方法建立了铝合金板材强度与应变强化指数n值的数学关系式。
1 实验材料与方法
实验材料为半连续铸造生产铝合金铸锭,其化学成分为(质量分数/%,下同):0.67Mg、1.35Si、0.64Cu、0.61Mn、0.11Fe,余量为Al。铸锭经540 ℃24 h均匀化处理后进行440 ℃热轧,随后进行中间退火,最终冷轧成1.2 mm厚的薄板。从冷轧板材上沿轧制方向切取试样,拉伸试样尺寸如图1所示。将拉伸试样品在540 ℃盐浴炉中保温30 min后水淬(固溶处理),然后分别在室温停放不同时间(0.17 h、0.5 h、1 h、2 h、3.5 h、4 h、24 h、96 h及336 h以上),或者分别在35 ℃时效1.5 h以及于70 ℃时效不同时间(4 h、8 h、12 h、24 h和48 h)。拉伸实验在SHIMADZU AG-X100KN电子万能试验机上进行,试样标距为50 mm,拉伸速度为4 mm/min,拉伸加载方向平行于轧制方向。
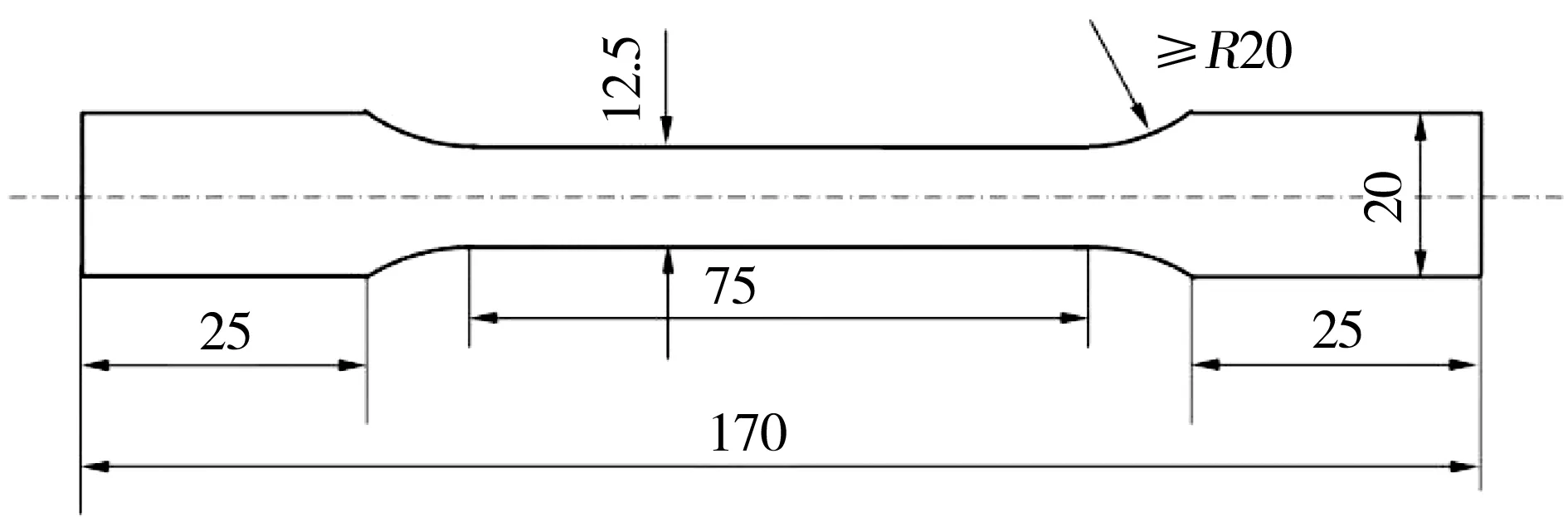
图1 拉伸试样尺寸(mm)Fig.1 Size of tensile specimen (mm)
认为铝合金板材的真应力-真应变满足Hollomon公式σ=K·εn或者lnσ=lnK+n·lnε(式中σ为真应力,K为应变强化系数,ε为真应变,n为应变强化指数)。n值的计算均是以屈服点(ε=0.2%)为计算起始应变,以均匀塑性变形范围内的任意一点(ε=i%)为计算终点应变,根据最小二乘法原理利用式(1)计算合金板材对应于不同计算终点应变的应变强化指数n。
(1)
式中:
N—计算应变范围内选取的计算应变点个数(本文计算应变点N的数量均为20个);
εi—计算应变点所对应的瞬时真应变;
σi—计算应变点所对应的瞬时真应力。
为区别不同计算终点应变的应变强化指数,将对应于不同计算终点应变量ε的应变强化指数n值记为nc,例如n10、n18分别表示ε=0.2%~10%和ε=0.2%~18%之间板材的应变强化指数。本文作者计算了n3、n5、n7、n10、n15、n18和n20作为研究对象。
2 实验结果
图2为Al-0.67Mg-1.35Si-0.64Cu-0.61Mn合金冷轧板材经540 ℃固溶水淬,然后分别在室温停放不同时间(0.17 h、0.5 h、1 h、2 h、3.5 h、4 h、24 h、96 h和336 h以上),或者分别在35 ℃时效1.5 h以及在70 ℃人工时效不同时间(4 h、8 h、12 h、24 h和48 h)的试样室温拉伸的工程应力-应变曲线。可见经不同工艺热处理后,合金板材的拉伸工程应力-应变曲线形状大致相似,在塑性变形初期均有比较明显的屈服平台,而且不同热处理状态试样拉伸曲线上的屈服平台长度不同(图2中虚线框所示)。说明合金板材中溶质原子均以位错能切割通过的固溶溶质原子或溶质原子偏聚区形式存在[17]。值得注意的是,固溶水淬后室温停放时间较短的合金板材试样的工程应力-应变曲线出现明显的锯齿现象,即Portevin-Le Chstelier,PLC效应(图2中实线框所示)。这是由于自然时效程度不充分,Mg、Si和Cu原子主要以随机分布的置换溶质原子固溶于铝基体中,对合金板材的强化作用较弱,合金板材的流变应力较低,运动位错、林位错与固溶溶质原子动态交互作用,造成运动位错反复被钉扎、脱钉,即发生了动态应变时效(Dynamic Strain Aging,DSA效应)[18-19],因此对于强度较低的合金板材流变应力曲线上出现明显的锯齿滑移现象。同时还可以发现经不同工艺热处理后的合金板材的强度差超过100 N/mm2,合金板材的屈服强度Rp0.2和抗拉强度Rm的变化范围分别为88 N/mm2~199 N/mm2和235 N/mm2~335 N/mm2,但是合金板材的强度整体偏低,这有利于板材冲压成形性的发挥。
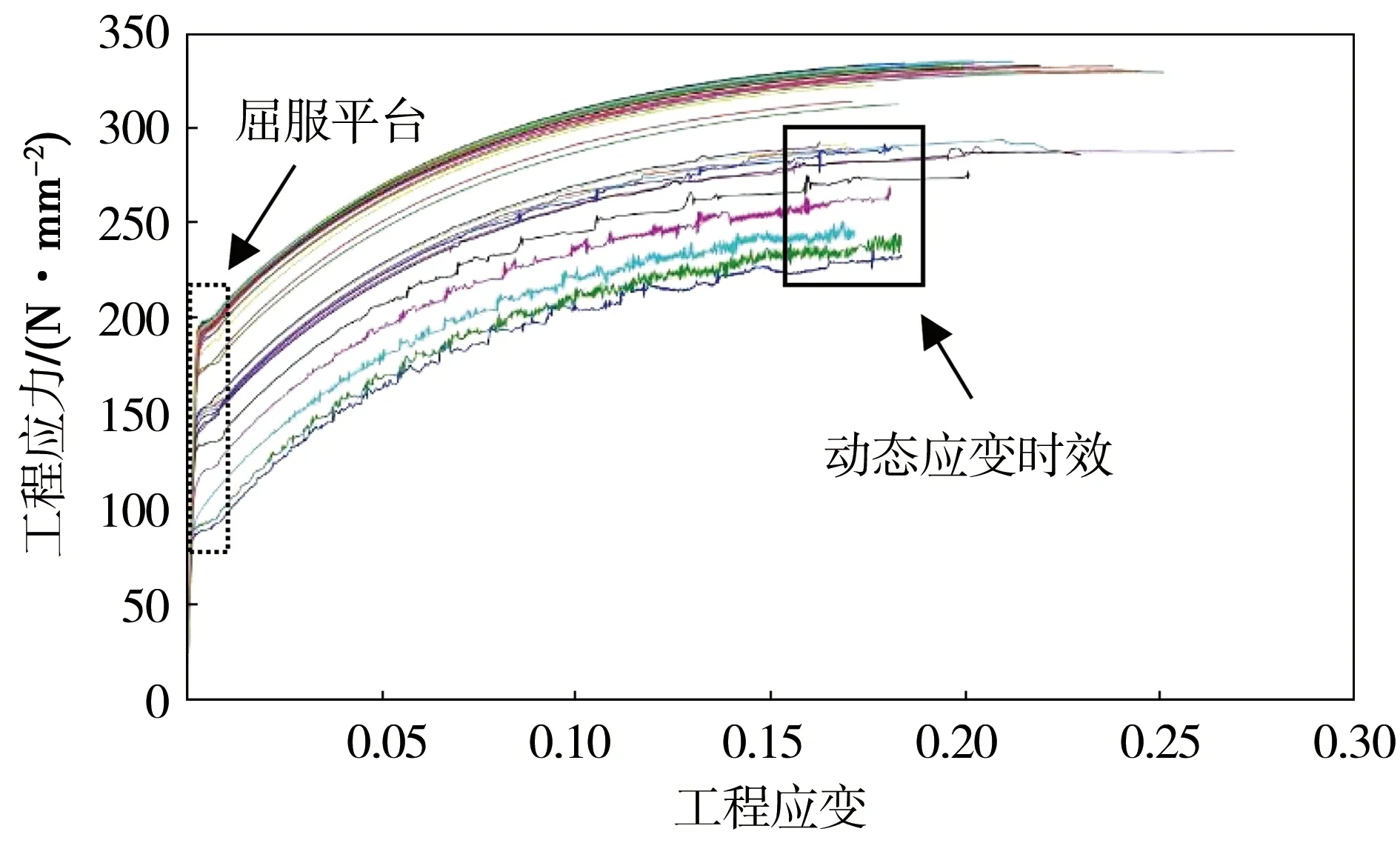
图2 经不同工艺热处理后的合金板材的工程应力-应变曲线Fig.2 Engineering stress-strain curves of alloy sheet subjected to different heat treatments
图3所示为Al-0.67Mg-1.35Si-0.64Cu-0.61Mn合金板材对应于不同计算终点应变的应变强化指数nc随合金板材强度增大的变化规律。可见合金板材对应于不同计算终点应变的应变强化指数nc随板材屈服强度及抗拉强度的增大均呈现出下降的趋势,尤其当计算终点应变超过3%后,nc随板材强度的增大呈现出线性降低的趋势。此外,对于固溶水淬后自然时效时间不超过24 h的合金板材拉伸变形时的应变较小未达到20%,因此对应于强度较低(Rp0.2≤140 N/mm2、Rm≤285 N/mm2)的合金板材的n20的实测点数量较少,但是仍然可以看出n20随合金板材强度增大呈逐渐减小的趋势。
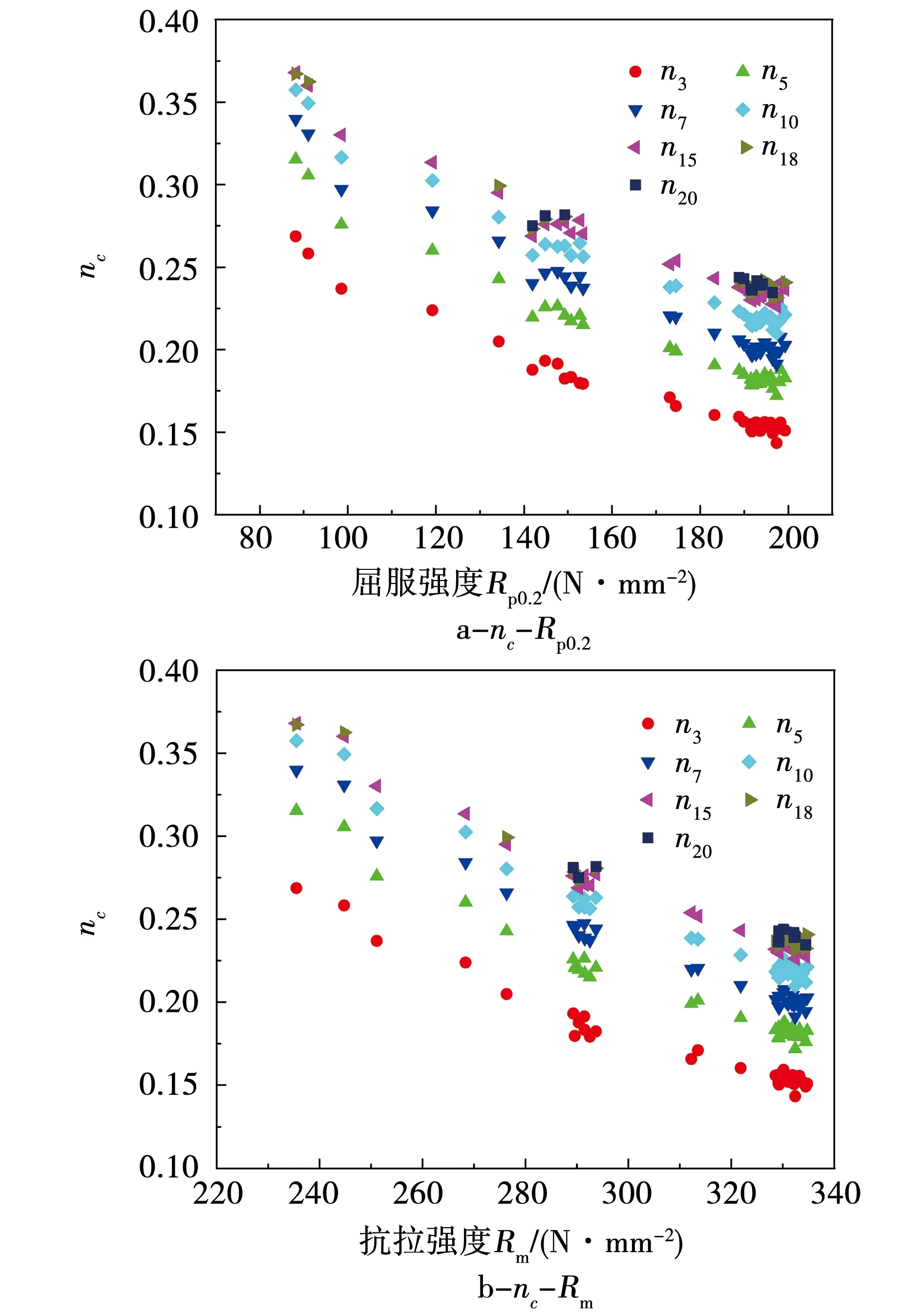
图3 对应于不同计算终点应变强化指数nc与板材强度的关系Fig.3 Relationship between nc and strength at different target strains of alloy sheet
3 分析及讨论
当Al-0.67Mg-1.35Si-0.64Cu-0.61Mn合金板材中强化合金元素主要以随机的固溶溶质原子或溶质原子团簇形式存在于铝基体中时,形成的溶质原子团簇越多对铝基体的强化作用越大,板材的强度越高,位错开动的流变应力越大,塑性变形过程中能够阻碍运动位错的障碍物相对减少,因而板材应变强化指数n值随强度升高而下降。由图3可知,Al-0.67Mg-1.35Si-0.64Cu-0.61Mn合金板材对应于的不同计算终点应变的应变强化指数n随合金板材强度的增大呈比较明显的线性降低关系,因此将对应于不同计算终点应变(3%≤ε<20%)的应变强化指数nc随板材强度升高的关系点进行线性拟合,结果如图4所示。可见,nc值与板材屈服强度Rp0.2及抗拉强度Rm的关系均可以满足式(2):
nc=f(ε)-kσ
(2)
式中:
nc—应变强化指数;
ε—真应变;
σ—真应力;
k—常数。
式中的ε为计算终点应变。对于已知计算终点应变的应变强化指数nc,式(2)可进一步简化为式(3):
nc=m-kσ
(3)
式中m、k均为常数。
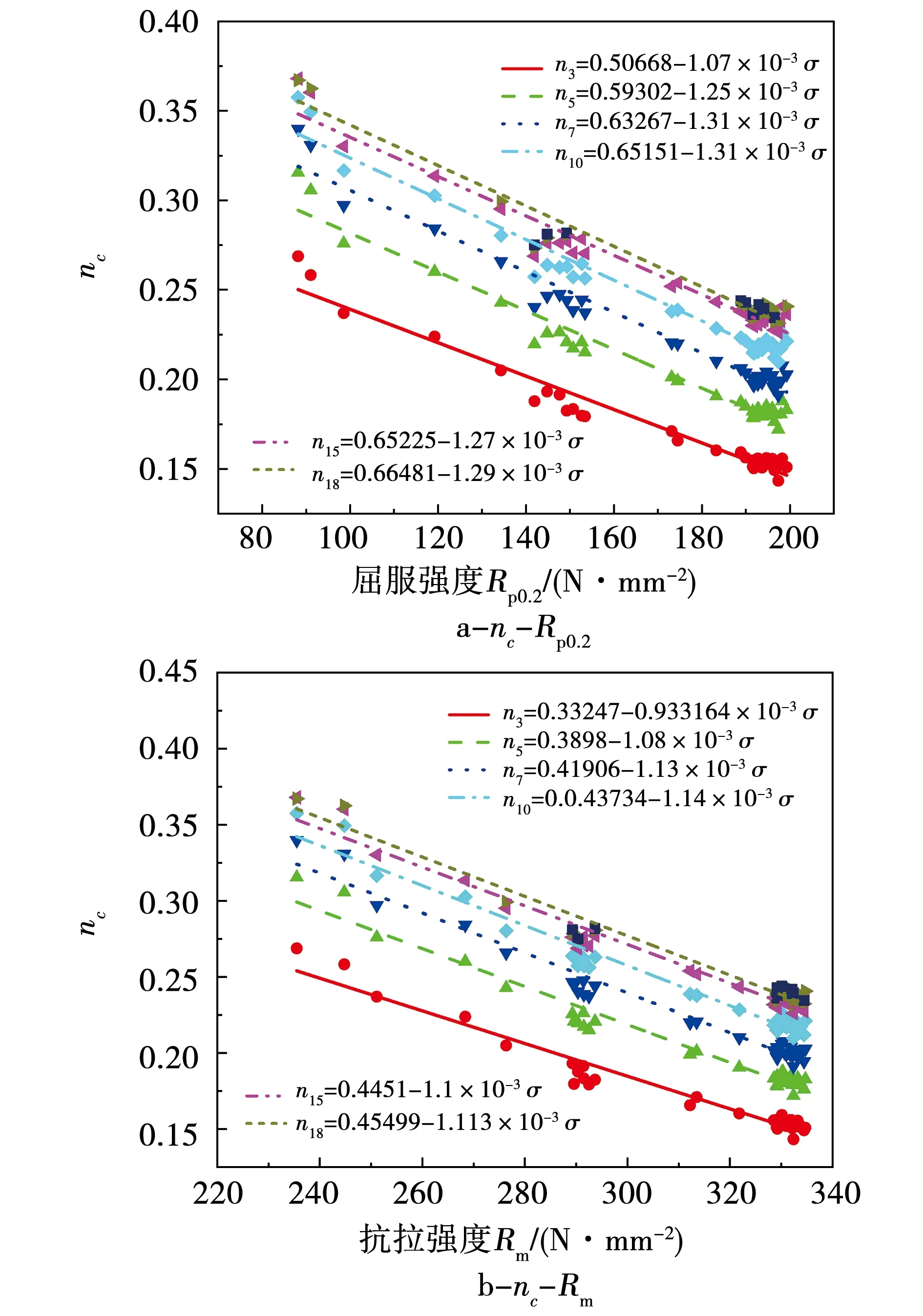
图4 对应于不同计算终点应变的应变强化指数nc随板材强度增大的拟合结果Fig.4 Fitting results of nc at different target strains with increasing strength of alloy sheet
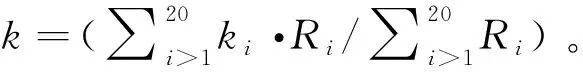

图5 nc=f(ε)-kRp0.2及nc=f(ε)-kRm中的f(ε)随计算终点应变ε的变化规律拟合曲线Fig.5 Fitting curves of f(ε) vary according to target strains ε in nc=f(ε)-kRp0.2 and nc=f(ε)-kRm
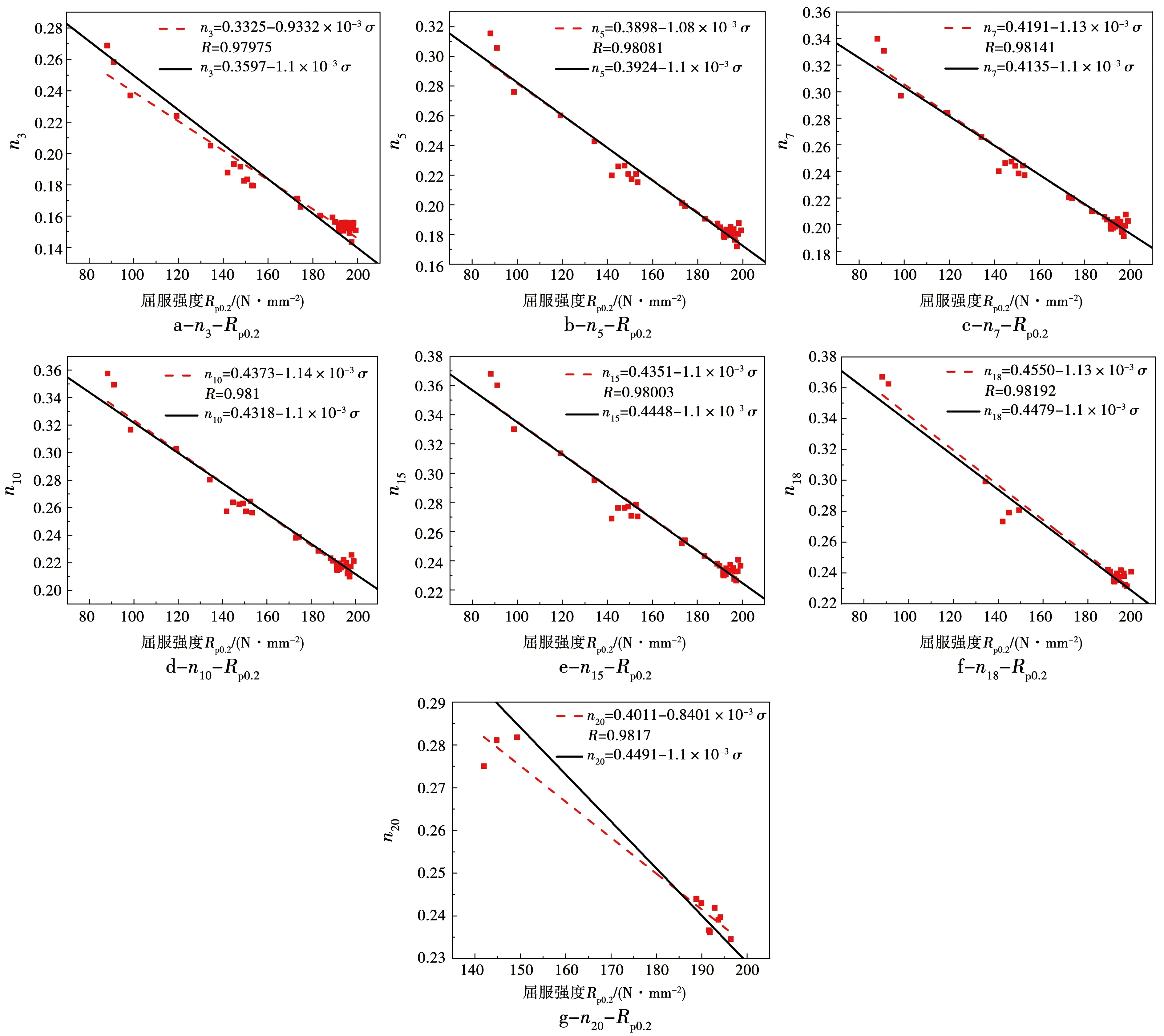
图6 合金板材对应于不同计算终点应变的nc-Rp0.2的计算直线(实线)与实测值拟合直线(虚线)比较Fig.6 Comparison between calculated result (solid line) and fitting result based on measured data (dot line) of nc-Rp0.2 at different target strains of alloy sheet
由图5确定出式(2)中的f(ε):
(4)
因此,式(2)可为:
(5)
对应于屈服强度Rp0.2,其参数的取值为:a0=0.4513,a1=0.1778,t=4.521,k=0.0011,即
(6)
对应于抗拉强度Rm,其参数的取值为:a0=0.6690,a1=0.1773,t=4.647,k=0.0013,即
(7)
为验证计算公式与实际结果的吻合程度,将板材对应于不同计算终点应变(ε≥3%)的应变强化指数nc与其屈服强度Rp0.2及抗拉强度Rm间的关系曲线的实测值直线拟合结果(虚线)与由式(6)和式(7)计算的结果(实线)进行对比,结果分别如图6和图7所示。可见,合金板材对应于不同计算终点应变(ε≥3%)的应变强化指数nc与其屈服强度Rp0.2及抗拉强度Rm均呈线性关系,且线性相关度均超过0.98。说明可以用式(6)和式(7)来预测Al-1.35Si-0.67Mg-0.64Cu-0.61Mn合金板材的n值与强度的关系。当合金板材的屈服强度Rp0.2和抗拉强度Rm分别小于100 N/mm2和240 N/mm2时,其n15值分别大于0.33和0.35。当板材的屈服强度Rp0.2或抗拉强度Rm分别升高100 N/mm2时,其nc将分别下降0.11或0.13。另外,当计算终点应变ε≤3%时,实测值直线拟合结果(虚线)与由式(6)和(7)计算的结果(实线)相差超过15%,其原因主要是由于当计算终点应变较小时,合金板材塑性流变处于不稳定阶段,nc测定的应变范围受合金板材屈服平台的影响程度较大(如图2虚线框),造成nc存在较大程度的波动;当计算终点应变超过18%后,实测值直线拟合结果(虚线)与由式(6)和(7)计算的结果(实线)相差超过20%,其原因主要是由于当计算终点应变非常大时,约67%的样品拉伸断裂前的最大应变均未能达到20%,因此nc实测点过少,导致实际拟合曲线的误差过大(如图3中“■”标识)。因此,由式(6)和(7)计算nc时,比较适宜的计算终点应变的范围应为3%<ε<20%。
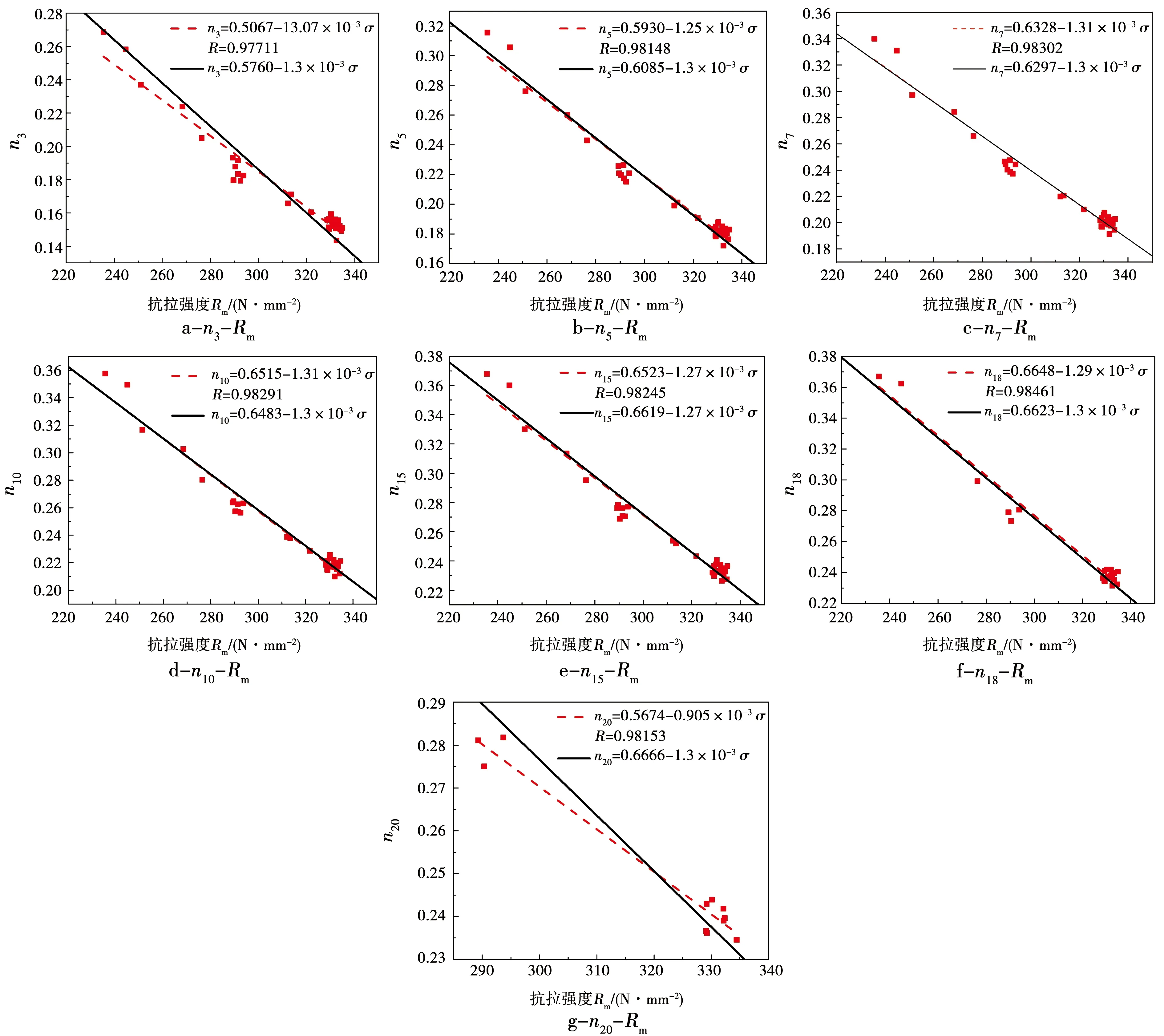
图7 合金板材对应于不同计算终点应变的nc-Rm的计算直线(实线)与实测值拟合直线(虚线)比较Fig.7 Comparison between calculated result (solid line) and fitting result based on measured data (dot line) of nc-Rm at different target strains of alloy sheet
4 结 论