基于PSO 与模糊PI 控制的永磁同步电机研究
2021-12-28邓豪
邓豪
(550025 贵州省 贵阳市 贵州大学 电气工程学院)
0 引言
永磁同步电机具有高功率密度、体积小、调速范围广等特点,被广泛用于工业控制、航空航天以及电动汽车领域[1]。在永磁同步电机的控制中,直接转矩控制是继矢量控制之后的另一种调速方案与矢量控制不同,直接转矩控制是将转矩和磁链作为控制变量,省去了复杂的坐标变换,因而其控制更加简单,动态响应更快。但是传统的直接转矩控制采用滞环结构,将导致转矩和磁链脉动较大,逆变器开关频率不固定,限制了其应用,因此许多学者提出了改进办法。文献[2-3]将开关表进行改进,使得在一个扇区中有多个有效电压矢量可以使用,但是可用电压矢量有限不能从根本上解决问题;文献[4-6]提出将空间电压矢量调制与直接转矩相结合,并用PI 控制来替代原有结构中的两个滞环比较器结构,使得开关频率恒定,转矩具有小的脉动,但是PI 控制对参数和负载变化敏感,鲁棒性差;文献[7-8]将滑模控制引入直接转矩控制。
由于滑模控制是变结构控制,对参数变化以及扰动不灵敏,鲁棒性好。由于直接转矩控制采用级联控制结构,速度环输出会影响转矩性能。传统速度环多采用PI 控制,当运行工况和参数发生变化时,PI 参数不能自适应调整。近年来,由于模糊控制和智能算法的发展,许多学者将其引入到速度环中。文献[9]将模糊控制引入速度环,同时使用遗传算法优化模糊规则,获得了更快的速度响应,但算法运用了复制、交叉、变异等操作,增加了计算复杂度;文献[10]使用改进正弦余弦算法对模糊控制量化因子和比例因子进行优化,具有良好的动静态响应;文献[11-12]使用粒子群算法对PI 参数进行整定,该算法简单、收敛速度快、参数调节少,获得了更好的调速性能。
综合以上分析,本文首先引入SVPWM 固定逆变器开关频率,使用滑模控制代替传统的滞环控制结构。设计了永磁同步电机速度环模糊控制器,引入粒子群算法,利用算法快速寻优能力优化模糊控制的量化因子和比例因子。最后在MATLAB/Simulink 建立了仿真模型,仿真结果表明,使用PSO 群算法优化模糊控制器参数较传统的PI,PSO-PI 有更好的动态性能和鲁棒性。
1 永磁同步电机直接转矩控制
1.1 永磁同步电机数学模型
为简化分析,建立一个理想的永磁同步电机数学模型,对PMSM 提出如下假设:忽略永磁同步电机铁芯饱和;忽略磁滞和涡流的影响;磁通势成正弦分布;忽略由于定子槽不规则所产生的影响[13]。
永磁同步电机在d-q 轴下的数学模型为

定子磁链方程为

式中:ud,uq——d-q 下的定子电压;id,iq——d-q下的定子电流;Ld,Lq——d-q 轴下的定子电感;R——定子电阻;φd,φq——d-q 下的磁链;φf——永磁体磁链;ωe——机械角速度;ω——电气角速度;pn——电机极对数。
电磁转矩方程为
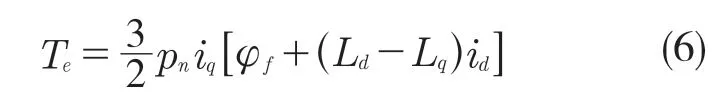
本文以表贴式永磁同步电机为例,因此Ld=Lq=L,所以新电磁转矩方程为

静止坐标下的磁链方程为

电磁转矩方程为

1.2 直接转矩控制
永磁同步电机传统直接转矩控制如图1 所示。转速外环采用PI 控制,转矩和磁链环采用滞环控制。直接转矩控制的本质采用定子磁链定向控制,通过判断磁链和转矩的增减来选择空间电压矢量。由于采用滞环比较控制会导致磁链和转矩脉动,逆变器开关频率不固定,在低速会受到定子电阻的影响等问题。为了获得更好的控制性能,引入滑模控制代替滞环控制。同时使用PSO 优化模糊控制对速度环加以改进,以此获得更好的动态响应,提高系统的鲁棒性。

图1 传统直接转矩控制Fig.1 Traditional direct torque control
1.3 Super-twisting 滑模控制原理
由于滑模控制对非线性系统具有良好的控制性能,并且对参数变化以及扰动不灵敏,物理上容易实现。为了减小传统直接转矩控制产生的磁链和转矩脉动,采用二阶super-twisting 滑模控制代替滞环控制,可以获得更好的控制性能和鲁棒性。定义切换函数如下:
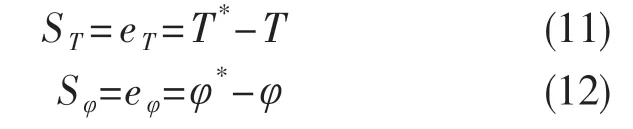
2 阶super-twisting 滑模控制包括两个方面:一个是滑动变量不连续函数;二是对时间求导的连续函数。2 阶super-twisting 滑模算法公式为

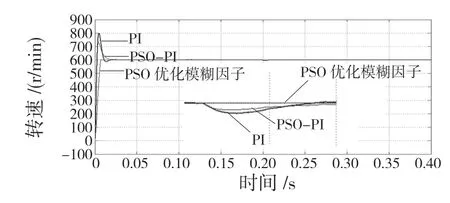
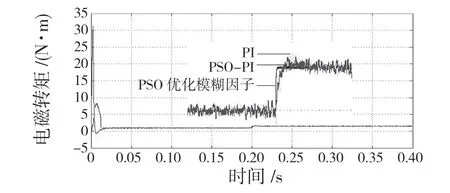
式(13)、式(14)中,Kp和KI表示增益,0 控制系统必须满足以下条件: 式中:Bm≤B ≤BM;AM≥|A|。 A 和B 需要满足式(17): 为了减小由于符号函数不连续切换带来的抖振问题,使用双曲正切函数代替符号函数。通过以上分析,转矩和磁链控制器如下所示: 传统PID 有结构简单、鲁棒性好、易于实现,被广泛应用于工业控制中,但是在实际过程中,其控制对象经常是非线性,时变,存在滞后环节,常无法获得控制对象的精确数学模型,使得传统PID 控制不能达到理想的效果,当系统存在外扰时,不能根据扰动的变化进行自调整。模糊控制通过模拟人脑,利用先验知识,能够实现PID 参数实时的调节,以此获得更好的控制性能。 模糊PI 控制器通常选取速度偏差e 和速度偏差的变化率ec 作为输入变量,∆Kp,∆Ki作为输出变量。两个输入变量的论域为(-6,6),∆Kp的论域为(-0.33,0.33),∆Ki的论域为(-15,15)。其模糊子集都定义为{NB,NM,NS,ZO,PS,PM,PB},即{负大,负中,负小,零,正小,正中,正大}。其中隶属度函数NB 选用“Z”型,PB 选用“S”型,剩余的都选用三角型。 模糊规则是模糊控制器的核心,模糊规则表建立的正确性将会一定程度上影响控制器的性能,模糊规则过少将会影响控制精度,过多会提高控制器的精度,但是规则过多,增加了推理过程的时间并且会占用大量的内存。一般而言,模糊PI 一般选用5 个或者7 个。根据实际经验我们可以得到e 和ec 与PI 之间的关系,可以总结出以下规律:在初期,误差e 较大时,可以适当增大比例系数KP;当误差e 变小,并且误差的变化率ec 符号与其变化率相反时,应当减小KP,适当增大Ki消除静态误差。当误差较小时,应该较小的KP,Ki避免系统发生震荡。最后得到模糊PI 规则表如表1 所示。 表1 模糊控制规则表Tab.1 Fuzzy control rule table 本文采用mamdani 进行推理,由于通过模糊规则所得到的值为模糊量,不能直接使用,需对其解模糊以得到控制所需的精确量,采用重心法进行去模糊化,公式为 式中:xi——论域中的元素;uN(xi)——模糊子集的隶属度函数。 在智能算法方面,PSO 作为一种新的智能优化算法,具有快速的收敛速度,调节参数少,简单易于实现,已经被应用于许多智能调参领域中。 粒子群算法是由美国社会心理学家Kennedy J和电气工程师Eberhart R 于1995 年提出的一种智能优化算法[14],其核心思想是通过模仿鸟类的觅食行为,将空间的每一只鸟抽象为一个粒子,每个粒子代表求解问题的可行解。多个粒子组成为一个种群,每个粒子都有各自的位置、速度和适应度函数值信息。在每次迭代的过程中,每个粒子根据自身位置、个体极值和全局极值来调整速度和方向。其速度和位置更新公式为 式中:ω——惯性权重,其大小表示空间的搜索能力;c1,c2——学习因子,通常设为1.5;r1,r2——(0~1)之间的随机数。 ω按式(25)进行自适应调整: 式中:ωmax,ωmin——ω的最大值和最小值,一般ωmax=0.9,ωmin=0.4;t ——当前迭代值;tmax——总的迭代值。 模糊控制对复杂、非线性、强耦合系统具有很好的控制效果,但仍有不足。模糊控制器一旦设计好,其参数就无法更改,这就导致不能根据各种工况实时调整。其中模糊控制的量化因子和比例因子在很大程度上影响控制性能,对多个参数凭借人工经验来调整,具有一定的盲目性,很难获得一组最佳的值。因此本文提出使用粒子群算法来优化模糊控制的量化因子(Ke,Kec)和比例因子(Kup,Kui),以此获得更好的控制性能。 图2 给出了粒子群优化模糊控制量化因子和比例因子结构图,在电机运行过程中,PSO 算法对4 个参数不断迭代优化,当满足最大迭代次数时,寻优结束,此时个体位置为4 个参数的最优值。具体步骤如下: 图2 粒子群优化模糊控制结构图Fig.2 Particle swarm optimization fuzzy control structure diagram (1)对粒子进行赋值,初始化种群为20,设置最大迭代次数为20。在本文中目标函数的空间为4 维,第i 个粒子在空间的位置表示为Xi=[xi1,xi2,xi3,xi4],速度表示为Vi=[vi1,vi2,vi3,vi4],其中第i 个粒子的个体最优位置为pid=[pi1,pi2,pi3,pi4],全局最优位置为pgd=[pg1,pg2,pg3,pg4]。 (2)选择适应度函数如式(26): 式中:R1,R2取值范围为(0~1);e ——速度误差;ec——速度误差的变化率。 (3)不断迭代找到最小适应度函数的粒子,该粒子在搜索空间的位置是最佳模糊控制的因子。 (4)输出最优参数值,经PSO 优化后的模糊PI 参数由式(27)、式(28)可得: 式中:KP0,Ki0——未加入模糊控制之前的参数;∆KP,∆Ki——优化之后模糊控制输出参数。 本文MATLAB2014a/Simulink 仿真所采用的PMSM 模型参数如下所示:定子电阻为R=1.2 Ω,电感Ld=Lq=0.008 5 mH,磁通φ=0.175 Wb,转矩系数为1.05 (N·m)/A,转动惯量J=0.000 8 kg·m2,极对数=4。转速环PI 原参数,P=0.05,I=20。 在Simulink 中建立基于PSO 优化模糊控制因子仿真模型,其中PSO 优化模糊控制参数模型如图3 所示。 图3 PSO 优化模糊控制量化因子和比例因子模型Fig.3 PSO optimized fuzzy control quantization factor and scale factor model 仿真中给定转速为600 r/min,定子磁链为0.3 Wb,负载初始值为1 N·m 在0.2 s 时变为1.5 N·m。仿真结果如图4 所示。 从图4 和图5 中可以看出,传统直接转矩转速具有较大的超调并且稳定时间较长,转矩在(0~1)之间脉动。 图4 传统DTC 转速Fig.4 Traditional DTC speed 图5 传统DTC 转矩Fig.5 Traditional DTC torque 从图6 中可以看出,在转矩和磁链环采用滑模控制的基础上,转速环采用传统PI 控制,转速具有快速的动态响应,能够在较短的时间趋近给定转速,但是具有很大的超调。通过使用PSO进行PI 参数整定,可以得到比传统PI 控制更好的动态响应,但是同样具有很大的超调。本文在采用模糊控制的基础上,使用PSO 算法对量化因子和比例因子进行调整,可以得到很好的控制效果,转速无超调,动态响应好,转速平稳。在0.2 s 时,负载发生变化。采用PI 控制,转速为590 r/min;PSO-PI 控制,转速为596 r/min;PSO 优化模糊控制因子,转速几乎没有变化。 图6 改进DTC 转速Fig.6 Improved DTC speed 由图7 可见,0.2 s 时,转矩发生变化且都有脉动。采用PI控制,转矩波动范围为1.35~1.65 N·m,转矩脉动为0.3 N·m。采用PSO~PI 控制,转矩波动范围为1.4~1.6 N·m,转矩脉动为0.2 N·m;在本文方法下,转矩波动范围为1.46~1.53 N·m,转矩脉动为0.03 N·m。 图7 改进DTC 转矩Fig.7 Improved DTC torque 从图8 传统方法中可知,传统直接转矩磁链脉动比较明显,范围在0.294~0.305 Wb 之间脉动;从图9 改进方法中可知,磁链曲线平滑,具有较小脉动,范围在0.296~0.304 Wb 之间。综上所述,在本文所提的方法下,转矩和磁链具有小的脉动,转速响应快,无超调,在负载变化的情况下可以很好地跟踪,改善了系统的动态性能。 图8 传统DTC 磁链Fig.8 Traditional DTC magnetic link 图9 改进DTC 磁链Fig.9 Improved DTC flux linkage 针对传统PMSM 直接转矩控制,磁链和转矩具有较大的脉动,使用二阶super-twisting 滑模控制代替传统的滞环控制,同时采用空间电压矢量控制固定逆变器开关频率。为了能够获得更好的转速响应,在传统的PI 控制下,转速具有大的超调,响应速度慢。提出使用模糊控制并采用PSO 算法进行调整量化因子和比例因子。运用Simulink 的仿真结果表明,与传统PI 和PSO-PI相比,磁链和转矩相比传统控制有较小的脉动,转速具有很好的动态响应,无超调,当负载突变时,抗干扰能力强。
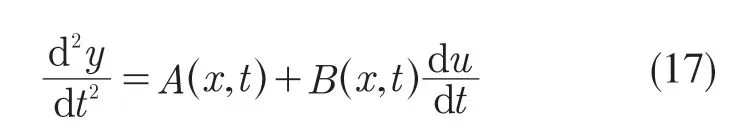

2 模糊PI 控制


3 粒子群算法

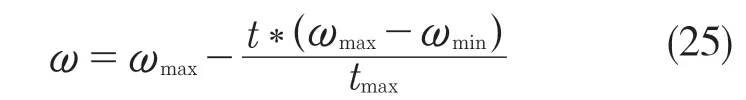
4 基于PSO 的模糊PI 控制器设计



5 仿真分析





6 结论
