滚动轴承边界润滑状态下沟道表面磨损演化研究

周锋财，佐景涛，陈观慈

（1.650500 云南省 昆明市 昆明理工大学 机电工程学院；2.150025 黑龙江省 哈尔滨市 中国航发哈尔滨轴承有限公司）

0 引言

滚动轴承由于摩擦阻力低、互换性好，被广泛用于各类旋转支撑[1]。滚动轴承受力通过滚动体和沟道承担，由于拖动力不足和接触变形等原因，滚动体-沟道接触区不可避免存在滑动现象，导致滚动体和沟道出现磨损现象。沟道的磨损将改变滚动体和沟道接触的表面形貌，从而进一步影响滚动轴承的使用寿命[2]，因此对滚动轴承进行磨损分析是有必要的。

Xue[3]等以Archard 磨损理论为基础研究了自润滑球轴承的磨损，并对轴承的摩擦力矩及磨损表现进行了研究；Milos Stankovic[4]、Ali R[5]等使用自适应有限元方法研究了滑动轴承接触的磨损仿真过程，结果表明滚动体和沟道的接触应力是变化的；Lorenza Mattei[6]等采用UMESHMOTION结合Archard 理论建立了磨损模型，重点研究了滑动磨损的演化过程；Arunachalam[7]等基于Abaqus 软件开发了一种去除材料轮廓的仿真技术，并进行了有限元模拟；金乐佳[8]等建立了轴承混合润滑下的磨损模型，并结合Archard 模型研究了轴承的磨损性能；霍亚军[9]基于Abaqus对球面滑动轴承进行了磨损有限元仿真，并结合实验验证了结果的正确性；高恒强[10]等通过球盘摩擦磨损试验，分析了轴承尺寸等各种因素对轴承磨损的影响；裴礼清[11]等为了揭示滚动轴承微动磨损的机理，对滚动轴承的接触滑动及接触应力进行了研究；苏文文[12]对自润滑关节轴承轴向游隙和衬垫磨损量的关系进行了研究。

当滚动轴承的润滑不充分或者在特殊条件下时，会出现边界润滑状态。此时轴承的摩擦系数较大，磨损比较严重。目前的研究对磨损演化过程分析较少，也没有考虑球-沟道的复杂运动关系对磨损演化的影响，没有考虑磨损过程中的滚动体与沟道的接触行为对磨损的进一步影响。基于以上分析，本文将选用边界润滑状态下接触界面相关摩擦参数，然后将滚动轴承的接触模型进行等效，接着采用UMESHMOTION 结合Archard磨损理论编写磨损子程序，最后对滚动轴承进行磨损演化分析，研究轴承径向载荷、球的自旋运动、陀螺运动和滑动等对沟道磨损损伤的作用，以及磨损后的沟道对轴承接触应力的影响规律。

1 球-沟道接触等效和磨损演化方法

1.1 球-沟道接触的等效方法

为节省计算时间，本文使用单个球和沟道的接触模型研究轴承沟道磨损的演化过程，同时为便于球-沟道接触模型的载荷和运动等边界条件的施加，在保证沟道接触应力大小和分布不变的条件下，将弹性的球和圆沟道接触等效为刚性球和弹性直沟道接触[13]，如图1 所示。

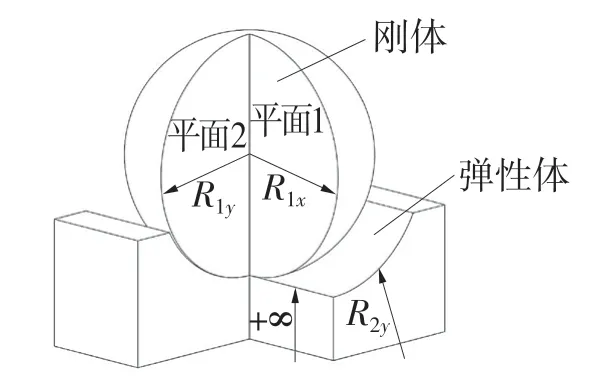
图1 球-沟道等效接触几何模型Fig.1 Ball-raceway equivalent contact geometry model

依据赫兹接触理论[14]，为了保证等效前后球-沟道接触椭圆大小不变，接触表面的曲率比值函数应满足式（1）。此外，为获得等效前后相同的球-沟道接触应力分布，球为刚性的情况，沟道材料的弹性模量可通过式（2）计算。

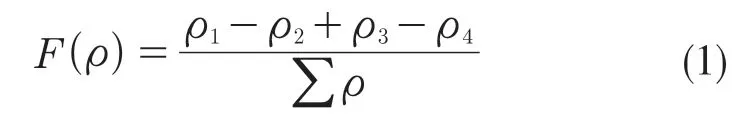
式中：ρ——表面曲率；∑ρ——接触表面曲率和函数。

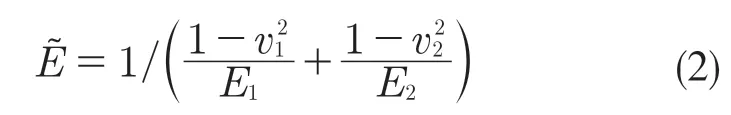
式中：v——材料泊松比；E——材料弹性模量。

本文所研究的球轴承的轴承沟道和球的材料为GCr15 轴承钢，材料弹性模量为207 GPa，泊松比为0.29，屈服强度为1 843 MPa[15]。轴承等效前后的结构和材料参数如表1 所示。

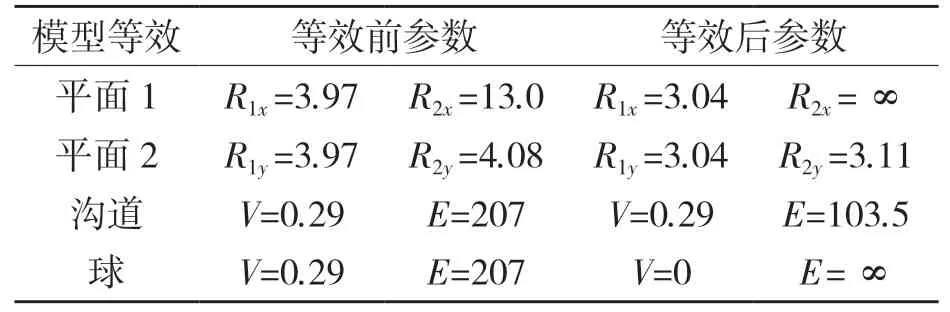
表1 轴承等效前后结构和材料参数Tab.1 Structure and material parameters of bearing before and after equivalent

1.2 磨损演化的分析方法

轴承的磨损通常出现在球与沟道的接触区域，在有限元分析中2 个接触面间的磨损是通过移动网格节点来模拟的，最终实现磨损表面慢慢被“磨掉”的整个过程。本文将调用Abaqus/Standard 模块下的UMESHMOTION 子程序计算节点的移动方向，使用Archard 磨损模型计算节点移动的距离，并结合ALE 自适应网格技术来控制滚道表面的节点移动以实现磨损演化。

磨损演化分析具体流程如图2 所示。

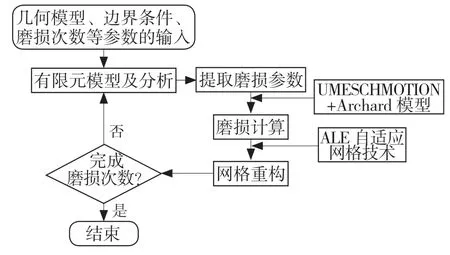
图2 磨损演化分析过程Fig.2 Wear evolution analysis process

第1 步：输入几何模型、材料属性、接触属性、边界条件、网格属性和磨损次数等参数。

第2 步：完成有限元建模并进行有限元接触分析。

第3 步：提取接触节点的坐标、接触应力和相对滑动距离。

第4 步：使用UMESHMOTION 结合提取的磨损参数计算出接触节点的磨损方向和磨损深度。磨损方向是接触节点的内法向方向，可由节点坐标计算求得。磨损体积可由Archard 模型[16]式（3）计算得出，磨损深度通过式（4）获得。接触节点在每个磨损增量中的磨损深度可由式（5）求得。磨损完成后接触节点总的磨损深度由式（6）得到。

式中：V——磨损体积；S——滑动距离；K——磨损比例常数；F——作用于表面法向力；H——材料硬度。

式中：KH——磨损系数，KH=；P——节点压力；V——节点滑动速度；t——磨损时间。

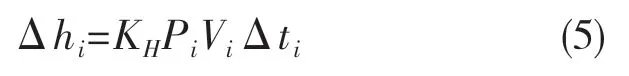
式中：Δti——磨损时间增量；Pi——该节点的接触应力；Vi——该节点的相对滑动速度。

式中：j ——完成磨损分析的总增量步数。

在ABAQUS 中，一个分析步代表一次磨损循环。滚动轴承的磨损往往是长时间造成的结果，轴承沟道在一个磨损循环过程中的磨损量是很小的，若一个分析步仅代表一次磨损循环过程，则整个磨损演化过程会产生成千上万个分析步。同时，由于沟道在一个磨损循环中的磨损量是很小的，沟道磨损后的表面几何形貌不会发生明显的变化，所以不会影响滚动体和沟道的接触应力分布和相对滑动距离。本文在此采用磨损加速方法，假设在经历M 次磨损循环内轴承的接触应力无明显的变化，则在M 次磨损循环中，每次磨损循环的磨损量是相同的。可以在Abaqus 中设置一个分析步为N（N ≤M）次磨损循环的结果。这将在不影响磨损结果精度的同时大大缩短分析计算时间。轴承在经历N 次磨损循环之后的磨损深度如式（7）。

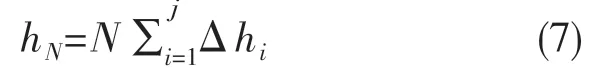
第5 步：调用ALE 自适应网格技术进行网格重构：首先通过扫描的过程进行网格重划分，节点沿磨损方向移动，移动的距离为磨损深度，再将旧网格中的变量信息转换到新的网格中，如此一次磨损完成。

第6 步：判断，若未完成规定的磨损次数，则继续进行下一次磨损循环。如果已完成规定的磨损次数，则分析结束。

2 轴承沟道表面磨损分析

2.1 不同径向载荷下的沟道表面磨损

为了研究不同径向载荷对沟道表面磨损的影响，对轴承分别施加300，400，500 N 的径向载荷，球滚动角速度为0.4 rad/s，边界润滑状态下摩擦系数取0.11，磨损系数取3.72×10-10[10]，磨损次数为10 万次。结合UMESHMOTION 磨损子程序进行分析。图3 和表2 给出了磨损结果。

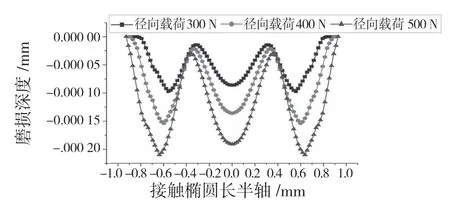
图3 沟道在不同径向载荷下的磨损深度（10 万次磨损）Fig.3 Wear depth of raceway under different radial loads (100,000 times of wear)

表2 沟道在不同径向载荷下的磨损体积（10 万次磨损）Tab.2 Wear volume of channel under different radial loads (100,000 times of wear)

从结果可知，随着径向载荷的增加，磨损宽度也随之增加，磨损深度越来越深，磨损体积也越来越大。当径向载荷为500 N 时，最大磨损深度为0.212 2 μm，磨损体积为0.000 132 mm3。

2.2 复杂运动形式下的沟道表面磨损

为了研究球在不同运动形式下沟道表面的磨损，给球施加1 rad/s 的滚动角速度以及径向载荷400 N。通常情况下，球很难在沟道里保持纯滚动运动，滚动轴承中的运动情况是复杂的。论文研究了球的自旋运动和滚动组合、陀螺运动和滚动组合、滑动以及滑动和滚动组合的复杂运动对轴承沟道的磨损影响。球的复杂运动会影响接触椭圆区域的滑动，图4（a）显示同时存在自旋运动和滚动时的滑动，细箭头代表滚动运动的滑动线，粗箭头代表自旋运动的滑动线，箭头的长度代表滑动量的大小；图4（b）显示同时存在陀螺运动和滚动时的耦合滑动线分布。

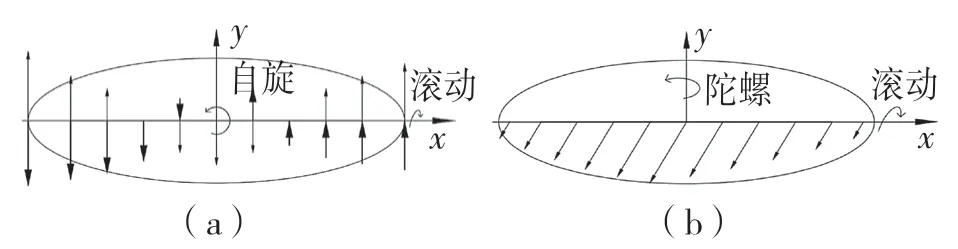
图4 接触区滑动线Fig.4 Sliding line in contact area

旋滚比是球自旋角速度与球相对于沟道滚动角速度的比值。图5 为轴承沟道在不同的旋滚比下的磨损情况。可以看出，由于自旋滑动和滚动滑动的耦合，轴承沟道右侧是主要被磨损的地方。在球旋滚比分别为0.10、0.25、0.50 时，沟道最大磨损深度为0.151，0.342，0.711 μm，沟道的磨损深度随旋滚比的增加而在增大。

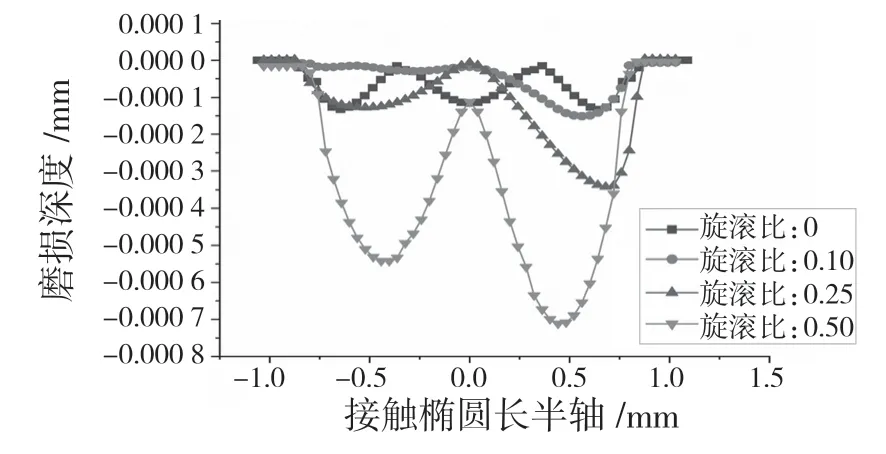
图5 球在不同旋滚比下沟道磨损深度（10 万次磨损）Fig.5 Wear depth of ball in lower raceway with different rotation ratio (100 000 times of wear)

在恶劣工况下滚动体的陀螺速度较大，较大的陀螺运动速度会使得沟道表面的摩擦力与接触椭圆长半轴方向相同。图6 为轴承沟道在不同的陀螺旋转速度下的磨损情况。

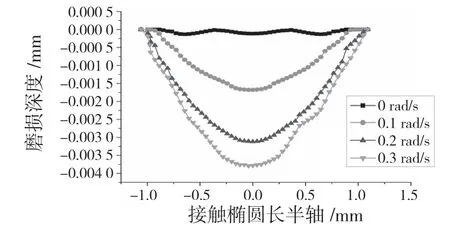
图6 球在不同陀螺速度下沟道的磨损深度（10 万次磨损）Fig.6 Wear depth of raceway of ball at different gyro speeds (100 000 times of wear)

在没有陀螺运动情况下，沟道的最大磨损深度为0.133 μm。由于陀螺滑动和滚动滑动的耦合，轴承沟道中心是磨损最严重的地方。在陀螺速度为0.1，0.2，0.3 rad/s 时的最大磨损深度分别为1.681，3.115，3.79 μm。由结果可知，当球有陀螺运动时的磨损情况比无陀螺运动时严重很多，并且随着陀螺速度的增加，磨损深度也在随之增大。

球与沟道的速度差导致球与沟道在接触位置发生接触滑动。图7 为轴承沟道在不同的滑动速度下的磨损率。由结果可知，沟道的磨损率随着滑动速度的增加越来越大。在没有滑动时，沟道的磨损率为0.001 83；当滑动速度在1 mm/s 左右时的磨损率变化不明显，磨损率在0.015 左右；当滑动速度为5 mm/s 时磨损率为0.078。

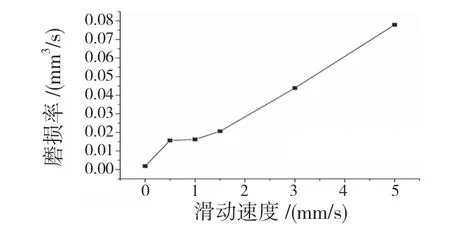
图7 球在不同滑动速度下沟道的磨损率（10 万次磨损）Fig.7 Groove wear rate of ball at different sliding speeds (100 000 times of wear)

轴承中的运动往往都是多种运动形式叠加在一起的，本文研究了滚动和滑动的组合运动对沟道磨损的影响。图8 给出了轴承沟道的磨损率情况。当球滚动时沟道的磨损率最小，球滑动时磨损率最大，滚动与滑动组合时沟道的磨损率居二者之间，为0.049 62。

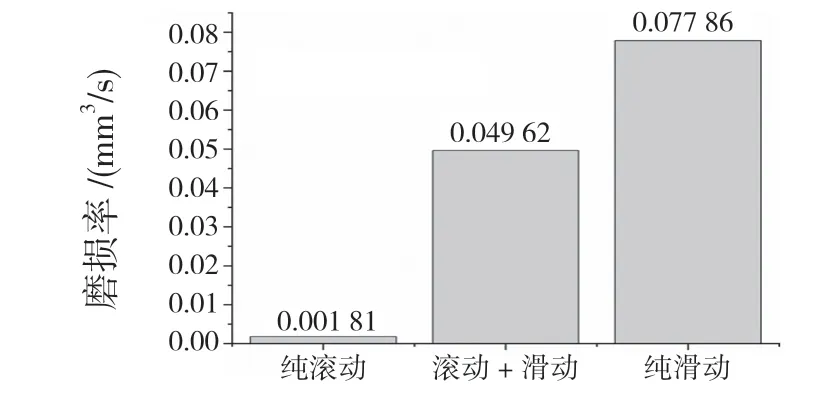
图8 滚动和滑动组合运动下沟道的磨损率（10 万次磨损）Fig.8 Wear rate of lower channel under combined rolling and sliding motion (100 000 times of wear)

3 接触行为和沟道表面磨损演化历程的交互作用

轴承沟道表面磨损之后其表面形貌会发生变化，球和沟道接触应力分布也会随之改变，进而又会影响下一阶段的表面磨损形貌。本文研究了轴承沟道在循环磨损100 万次过程中沟道表面磨损形貌的演化情况。对球施加1 rad/s 的滚动角速度以及径向载荷400 N。图9、图10 给出了轴承沟道在随着磨损次数的增加时表面磨损的演化结果以及磨损率情况。

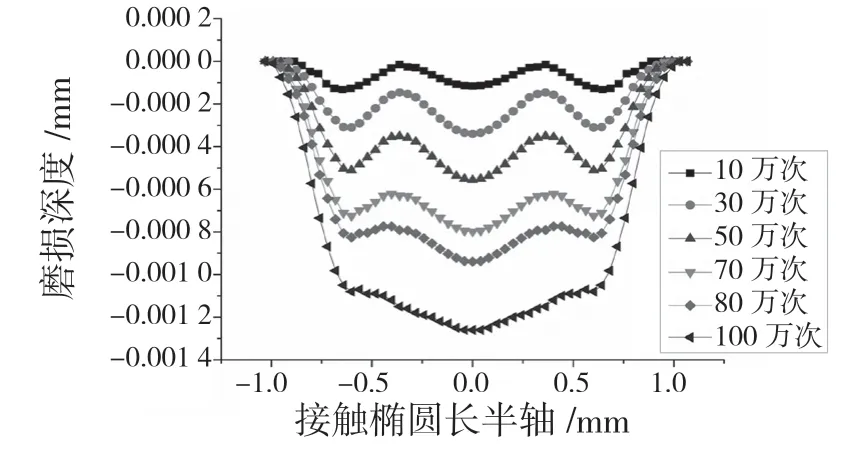
图9 沟道表面磨损演化历程Fig.9 Evolution of raceway surface wear

从图9 可知，随着磨损次数的增加，沟道表面磨损越来越严重，表面磨损宽度也在增加。磨损10 万次时，磨损宽度为1.75 mm；磨损到100万次时，磨损宽度为1.98 mm。在磨损过程中，滚道x=±0.6 处和x=0 处的磨损出现了一个互相竞争的过程，在磨损到70 万次时，x=0 处的磨损量已经超越了x=±0.6 处的磨损量，且在后续磨损阶段中二者磨损差量逐渐变大。对于纯滚动点处，其磨损率随着磨损的进行越来越快，直到100 万次磨损时，纯滚动点处的磨损已经超过了x=±0.6 处的磨损。从图10 可知，沟道的磨损率随着磨损循环次数的增加逐步增大，沟道发生破坏的时间越来越短。

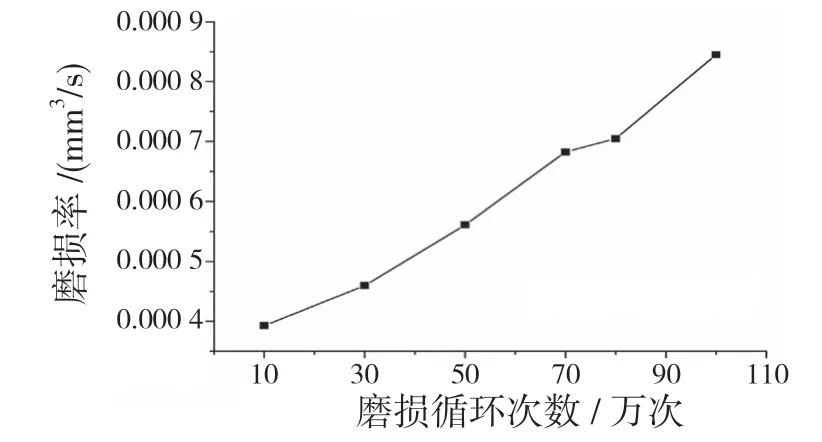
图10 沟道磨损率随磨损历程变化结果Fig.10 Changes of raceway wear rate with wear history

由磨损演化历程分析可知，轴承沟道表面的磨损情况会随着时间推移变得更加恶劣，所以找出轴承在磨损时的规律是有必要的。本文提取沟道在每一个载荷循环过程中的最大接触应力，以此验证在磨损过程中球与沟道的接触是否会发生变化。图11 为轴承沟道在磨损循环过程中的最大接触应力。随着磨损次数的增加，球与沟道的最大接触应力变得越来越大，磨损越严重接触应力变化越明显，磨损到100 万次时最大接触应力达到了1 688 MPa。这为后期的轴承磨损诊断提供了一定的理论依据，即当轴承最大接触应力越来越大时，说明此时轴承沟道的磨损比较严重。

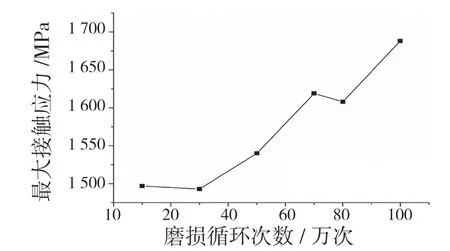
图11 沟道最大接触应力随磨损历程的变化结果Fig.11 Variation of raceway maximum contact stress with wear history

4 结论

（1）分析了轴承在边界润滑服役状态下，球的复杂运动对沟道表面磨损的影响。结果表明，球的复杂运动会影响接触界面的摩擦学行为，进而影响沟道的磨损形貌。随着球旋滚比、陀螺速度、滑动速度的增加，沟道表面磨损程度也相应增大，其中陀螺运动和滑动对沟道磨损影响最大。

（2）研究了接触行为和沟道表面磨损演化历程的交互影响。结果发现，沟道表面磨损后将不再是光滑曲面，而是会产生局部凸峰和凹坑，导致球与沟道不再是赫兹接触，进而影响下一阶段的磨损形貌。沟道磨损随着磨损演化历程恶化得越来越快，到100 万次磨损时，沟道磨损率达到了0.000 85，比初始磨损率增加了115%。

（3）得到了轴承沟道在磨损演化历程中接触应力的变化规律，即磨损循环次数增加时，轴承最大接触应力也随之增大，当磨损100 万次后，沟道最大接触应力达到了1 688 MPa，比磨损前的接触应力增加了16%。