发动机悬架热固耦合计算与结构优化

朱露，仲梁维

（200093 上海市 上海理工大学 机械工程学院）

0 引言

发动机悬架是连接发动机和汽车车身的重要部件，对发动机起着支撑、缓冲的作用，其性能对于汽车安全运行至关重要。节能减排是汽车行业可持续发展的重要条件，在满足各项性能的前提下对汽车零部件进行轻量化是实现这一目标的有效途径之一。

国内外对发动机悬架的研究主要集中在振动特性上[1-2]，对其受到机械力影响的研究较少。本文开展了对悬架的热-固耦合分析，研究其在受到温度和发动机机械力作用下热应力分布情况。结果显示，悬架侧脊处存在较大的应力集中，选择对悬架的4 个主要尺寸进行参数化优化以及整体的拓扑优化，使得侧脊处最大应力减少了90.28 MPa，悬架整体质量减少了10%。

1 发动机悬架热应力分析

1.1 热力学分析的基本原理

实际工况下发动机悬架所受传热方式主要为热传导与热对流。悬架由于与发动机直接接触且存在温度梯度，其引起的热量传递为热传导过程。傅里叶定理指出，对于某一方向热通量可以表示为

式中：q——热流密度；Knn——沿n 方向的热传导系数，W/(m·K)；∂T/∂n——温度梯度。系数前的负号表示热流方向与温度梯度方向相反。

并且，由于悬架同时与周围空气存在温度差，对流换热的情况也会伴随着发生，根据牛顿冷却定律可得

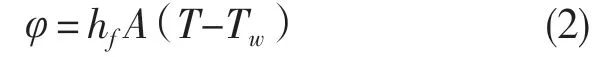
式中：φ——对流传热速率；hf——对流换热系数，W/m2℃；T——模型表面温度；Tw——邻近流体的温度。

1.2 建立有限元模型

该发动机悬架由两个托架和一个连接销轴组成，材料采用低合金结构钢Q345，材料参数如表1 所示。

表1 Q345 材料参数Tab.1 Q345 material parameters

有限元的求解过程是利用数学近似的方法对真实物理系统进行模拟，利用简单而又相互作用的元素，以有限数量的未知量去逼近无限未知量的真实系统[3-4]。该支架的单元尺寸设置在1.5 mm，网格类型采用自动划分方式（Automatic），划分完成后可以得到107 853 个单元和176 629 个节点，此时几何模型转变为具有物理属性的有限元单元。

1.3 施加边界条件

求解热应力需要先后对发动机悬架施加温度场求解的边界条件和静力分析边界条件，利用ANSYS Workbench 的热-固耦合功能得到最后热应力分布云图。

首先施加悬架温度场求解的边界条件。在发动机与托架接触部位施加65 ℃的温度载荷并且对托架和连接销轴都施加对流负载，在悬架温度场求解结束后施加应力求解的边界条件。在连接轴两端的螺纹孔内侧设置固定约束（Fix Support），根据实际情况在两边托架的螺纹孔施加发动机给悬架的机械力，具体如图1 所示。

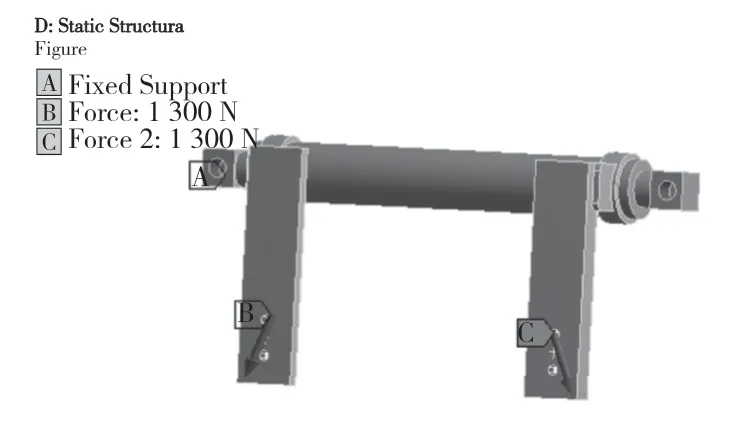
图1 应力场边界条件Fig.1 Boundary conditions of stress field

1.4 查看结果

在施加了温度场边界条件后，发动机悬架的温度场分布如图2 所示。

图2 悬架温度场求解结果Fig.2 Results of solving suspension temperature field

在温度场求解结束后，通过热-固耦合模块将温度场的计算结果输入至接下来的应力求解过程中去[5]，得到的该发动机悬架的热应力结果如图3 所示，位移变形结果如图4 所示。

图3 悬架热应力云图Fig.3 Suspension thermal stress nephogram

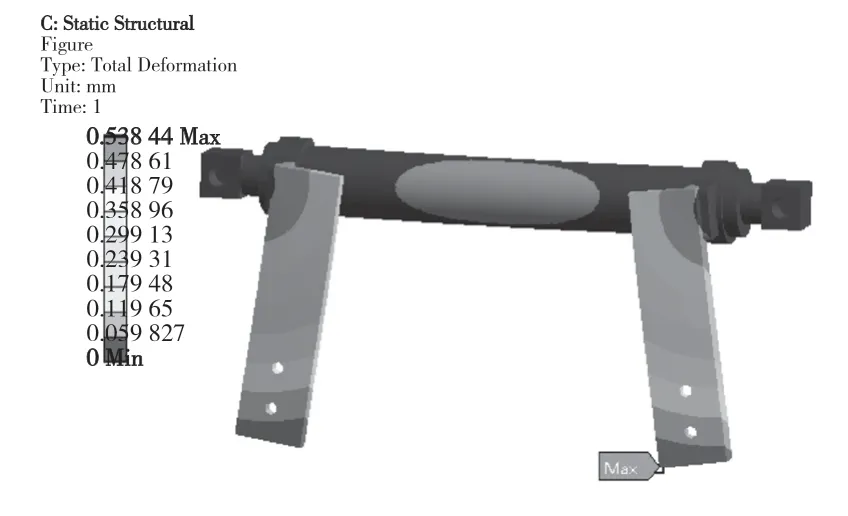
图4 悬架变形位移云图Fig.4 Suspension deformation displacement nephogram

从发动机悬架热应力云图中可以看出，最大应力出现在侧脊处，为358.34 MPa，已超过材料的屈服极限值345 MPa 并引起结构的损坏，需要对结构进行优化设计。

2 优化分析

2.1 优化分析介绍

由于最大热应力集中在托架侧脊处，考虑到托架加工工艺的可行性，选择在托架弯折直角处增加2 mm 圆角，并利用Workbench 优化模块对其中3 个侧脊处的圆角进行寻优找到最佳取值，以减小应力集中。

ANSYS Workbench 中提供优化设计的平台为Design Exploration，它可以描述设计变量和产品性能指标之间的关系，并可以得到一些曲线、曲面、敏感图来帮助用户选择合适的设计点[6]。本文采用响应曲面优化（Response Surface Optimization）方法，其优点在于不用完全运行整个求解过程就可以得到输出参数的近似值[7]。

以下几个因素会影响到响应曲面的精确度：求解过程的复杂程度、响应曲面类型、选取的设计点数。若要判断分析结果是否可靠，可以通过查看响应曲面精度。通常在计算前可以提前设定各设计点之间的偏差上限（如5%），当计算完成后，各设计点之间的结果低于这一个值，就可以认为计算结果是可靠的，即响应曲面的精度得到了保证。精度的提高通常采用增加设计点的办法，但在进行实验设计前，通常只能在一定程度上定性地确定输入、输出参数间的关系，如果一味盲目地增加设计点数会提高计算工作量，增加不必要的计算时间[8]。

优化分析的数学模型可以表示为

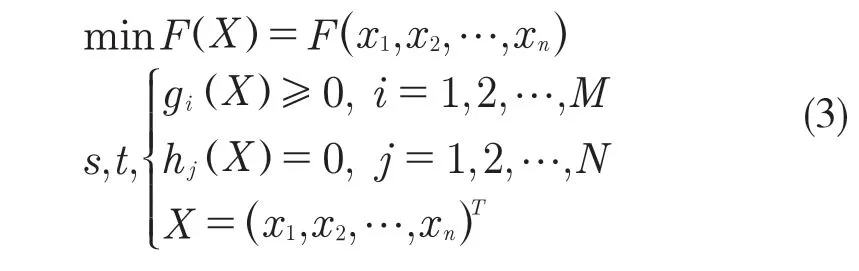
式中：X——设计变量；F（X）——目标函数；gi（X），hj（X）——状态变量。

2.2 响应曲面优化

对侧脊的3 个圆角尺寸进行优化，分别选取“圆角1”“圆角2”“圆角3”“托架厚度”为4 个输入参数。优化目标是降低侧脊的热应力值的大小使得安全因子大于1.2，则规定悬架的最大等效应力（即热应力）“Equivalent Stress Maximum”以及悬架总位移“Total Deformation Maximum”为两个输出参数。

系统会预先对各个输入参数给出变化范围，通常是原值的10%上下浮动，也可以根据具体情况进行调整。本文中在各值不发生干涉的条件下，将“圆角1”与“圆角3”变化范围均设置在1～3 mm（初始值2 mm），“圆角2”变化范围为1.5～2 mm（初始值2 mm），“托架厚度”变化范围为4.5～5.5 mm（初始值5 mm）。设置完成后，更新实验设计组件，系统自动生成了25个设计样本，每一个设计样本即代表了一种设计方案。计算完成后可以根据得到的点绘制相应的曲线和曲面。图5 所示为悬架热应力随参数“圆角1”和“圆角3”的响应曲面图。

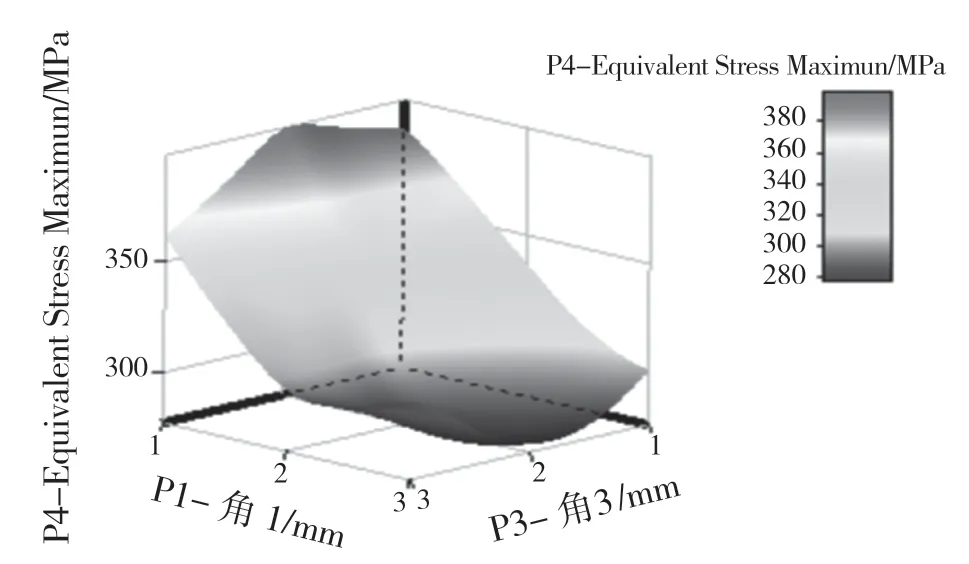
图5 热应力响应曲面图Fig.5 Thermal stress response surface

通过局部灵敏度图可以清楚直观地看出产品性能指标是怎样随设计参数变化的。从图6 中可以看出，圆角1 的值对最大等效应力影响最大且二者关系呈负相关，意味着热应力随圆角1 的值增大而减小；对悬架总位移影响最大的是托架的厚度，随着托架厚度的增加悬架总位移减小。

图6 局部敏感图Fig.6 Local sensitivity map

2.3 几何尺寸优化结果

计算完成后可以得到系统寻找的符合优化目标的3 个推荐点，这些推荐点基于优化目标进行评价，星号越多就表示越符合我们设定的目标，如图7 所示。通过比较得出Candidate Point 2 是最好的。

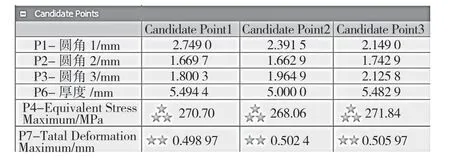
图7 优化结果Fig.7 Results of optimization

表2 则为优化前后吊钩的设计参数对比。最大应力由358.34 MPa 减小到285.24 MPa，减少了20.4%，安全系数由0.96 提高到1.22。

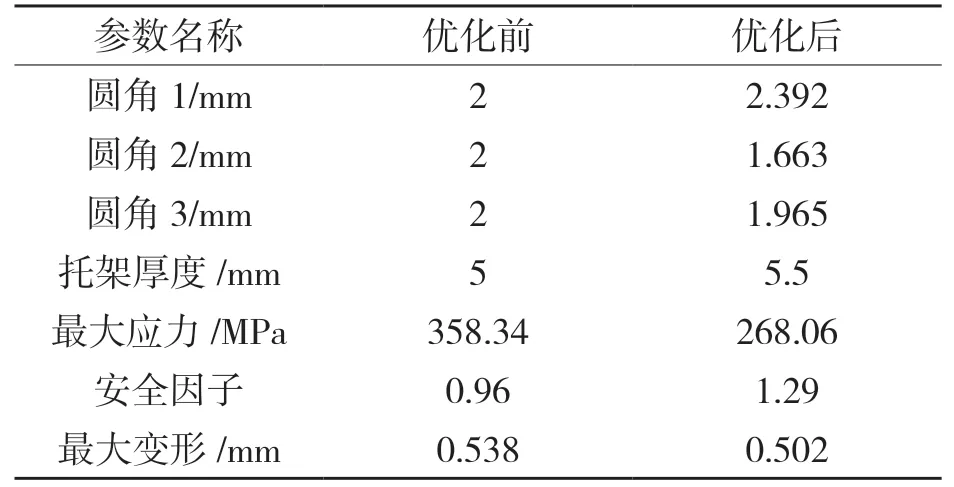
表2 吊钩优化前后对比Tab.2 Comparison of hook before and after optimization

3 拓扑优化

拓扑优化设计就是根据结构分析所得到位移、应力分布等结果对结构进行重新设计，例如确定连续体内有无孔洞以及孔洞的位置、数量等在工程结构的应力、体积、位移等，设计的目标是得到一个材料的最佳分布结构[9]，其优化结果一般比较复杂并且呈多样性，可以按照以下原则对原结构进行设计[10]：（1）螺栓连接区域附近应该保持不变；（2）材料堆积超过工艺要求的需适当挖空；（3）零件设计应包络优化后的材料分布空间；（4）优化后有明显加强筋特征的应完整保留到后续详细设计中去；（5）结合以往经验和现有设计进行优化。

设置去除比例为20% 的条件下ANSYS Workbench 对悬架的优化情况如图8 所示。综合系统参数化优化结果、拓扑优化结果和设计原则最终的三维模型如图9 所示，通过减重10%实现悬架轻量化目标。

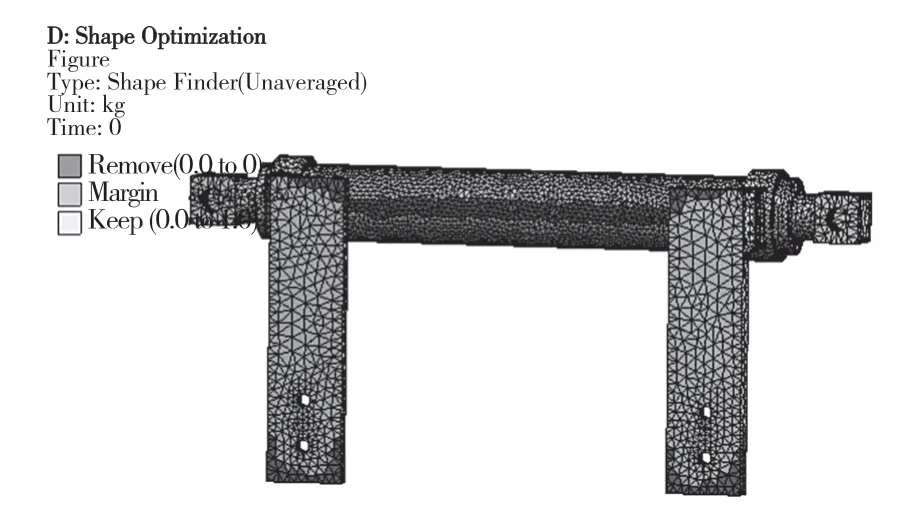
图8 拓扑优化后结果Fig.8 Results of topology optimization

图9 综合优化结果后的最终三维模型Fig.9 Final 3D model after comprehensive optimization results

综合两次优化之后应力分析结果如图10 所示。在轻量化的基础上结构的应力集中情况得到改善，最大应力由358.34 MPa 降到了278.38 MPa，进一步延长了发动机悬架的产品使用寿命，并提高了汽车运行的安全性。

图10 优化后发动机悬架的应力云图Fig.10 Stress nephogram of optimized engine suspension

4 结语

本文利用ANSYS Workbench 协同仿真平台对某品牌发动机悬架进行了有限元分析、参数化优化设计和拓扑优化设计，其目的在于改变悬架的结构参数，在工作过程中减小应力集中，提高悬架安全因子延长其使用寿命，并实现了轻量化为能源节约做出贡献。此外，三维建模软件与ANSYS Workbench 的配合使用，大大缩短了产品的设计周期，降低了研发成本。