基于拓扑优化的机床立柱设计

孙文辉，李天箭

（200082 上海市 上海理工大学 机械工程学院）

0 引言

随着现代制造业的高速发展,机床各个部件都在往高精度与高性能方向发展[1]，不仅要求机床部件的精度要高，还要求其性能更好[2]。机床在工作时，立柱对整个机床的模态、刚度都起到很重要的作用，还能起到支撑整个机床结构的作用，因此立柱的刚度以及固有频率大小对机床来说很重要。

机床的性能固然重要，而对于机床部件的设计，大多数设计者还都只停留在经验设计与结构类比的阶段[3-4]，这可能不会使设计部件的性能提高更多，拓扑优化技术可以目标性地提高结构的性能，能给零件的结构设计提供有效的参考，在机床的零部件结构的设计中已经得到广泛应用[5]。拓扑优化技术可以使构型内部的力流更加有效地传递，还可以减少材料属性，缩减成本，所以从轻量化与经济效益方面着手[6]，拓扑优化技术有一定的优势。

在本文中利用拓扑优化技术，通过有限元软件ANSYS Workbench 对立柱进行拓扑优化。在考虑到机床工作时，立柱与主轴箱的连接部位会有多种工况产生，这时要分3 种不同情况分析，从而在以提升一阶固有频率为目标的前提下，得出理想的立柱构型。

1 立柱有限元模型建模

机床由很多部件组成，其中包括床身、立柱、主轴箱、主轴、工作台等几大部分。本文主要研究机床立柱的性能。一般机床的内部都是空心的，在本文中建立的有限元模型是实体的结构，对建立的实体的模型进行拓扑优化，得出一定的构型，对新的模型重新计算与重构，从而设计出满足一定要求的立柱模型。立柱的有限元模型实体结构如图1 所示。此模型为长360 mm，宽460 mm，高120 mm，且主轴箱位于上工况位置时的一种情况，连接部位简化为上工况受力面。

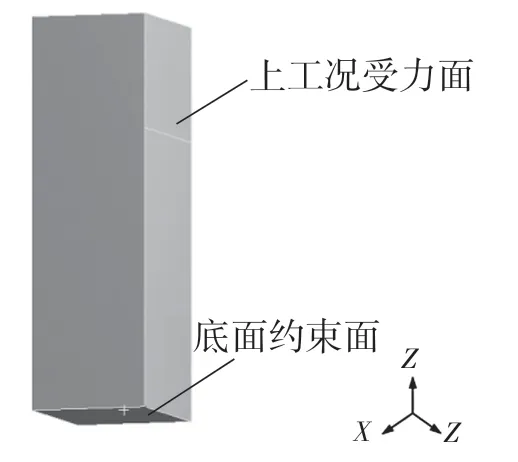
图1 立柱实体结构Fig.1 Column structure

建立有限元模型后，将立柱实体结构模型导入ANSYS Workbench 中，将材料设置为铸铁。铸铁的密度为ρ=7.2×103kg/m3，泊松比为μ=0.28，弹性模量为E=110 GPa。将立柱模型划分单元网格，单元数25 254 个，节点数109 966 个。进行模态分析，模态分析时将底面约束面固定住，经过分析可以得出此模型的前6 阶固有频率。各阶固有频率如表1 所示。

表1 立柱前6 阶模态的固有频率Tab.1 Natural frequencies of the first six modes of column

其中1 阶振型如图2 所示。

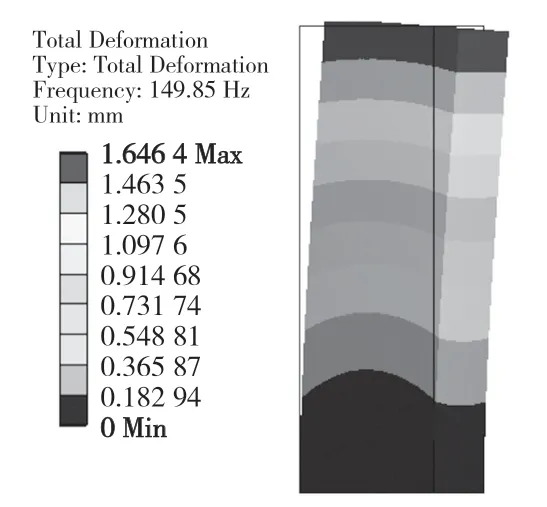
图2 1 阶振型Fig.2 First mode

2 拓扑优化

2.1 拓扑优化数学模型建立

拓扑优化的方法有很多种，本文采用的是变密度法对模型进行拓扑优化，以最大刚度为目标，提升一阶固有频率。

材料宏观物理量与材料的密度之间存在非线性关系

式中：Ei——单元i 弹性模量；μ0——材料的初始泊松比；μ——泊松比；p——密度惩罚因子，常取p=3；ρi——单元相对密度。

变密度法的数学模型如式（2）-式（3）：

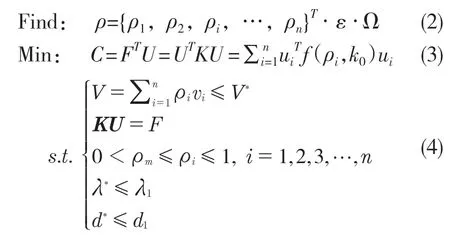
式中：ρ——单元密度单位向量；n——结构里面单元的数量；K——结构总刚度矩阵；F——节点处载荷；U——位移产生的向量；C——结构柔度值；ui——单元i 节点位移向量；k0——刚度矩阵常量；ρm——相对密度最小的变量；λ1——1 阶固有频率；λ*——原始1 阶固有频率；d1——最大变形位移；d*——原始最大的变形。

2.3 三种工况下拓扑优化

机床工作时，立柱部分既要考虑底部与底座相接触部分，也要考虑侧面与主轴箱接触部分。底面部分可以采用固定端约束，而侧面则需考虑其受力情况。而在机床工作时往往会遇到多种加工工况，这样就要考虑机床在多种工况下拓扑优化的情形，这里采用立柱部分与主轴箱部分连接在一起的情况来进行研究。由于机床运转的多样性，采用主轴箱位置在上工况位置、中工况位置与下工况位置3 种情况分别进行拓扑[7]，探究立柱的拓扑结构变化与规律。3 种工况如图3 所示。

图3 上、中、下三种工况Fig.3 Upper,middle and lower working conditions

对3 个模型分别添加载荷与约束，如图4 所示。C，D 四个面受力大小方向一致。A 为向下的重力作用，B 为主轴下端面模拟加工受的三项力，C 为多工况运行轨道受三项力，D 面为固定约束面。

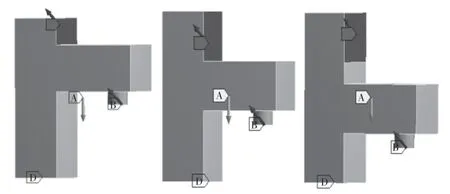
图4 模型受力Fig.4 Model stress

分别进行35，35，31 次迭代之后得出其拓扑结果，如图5 所示。

图5 三种工况拓扑结果Fig.5 Topological results of three working conditions

2.4 立柱计算外力与单独拓扑

上述情况为多工况情况，是由立柱加主轴箱两部分结合在一起进行分析，现就立柱部分在拆开之后，需要考虑力通过主轴箱传递给立柱[7]，力的大小在立柱右侧面的分布情况进行研究，在其他面受力不变情况下，探讨主轴箱与立柱接触部分的力传导情况。以上工况为例，即主轴箱与立柱接触面在立柱右侧的最上端，其受力情况如图6 所示。

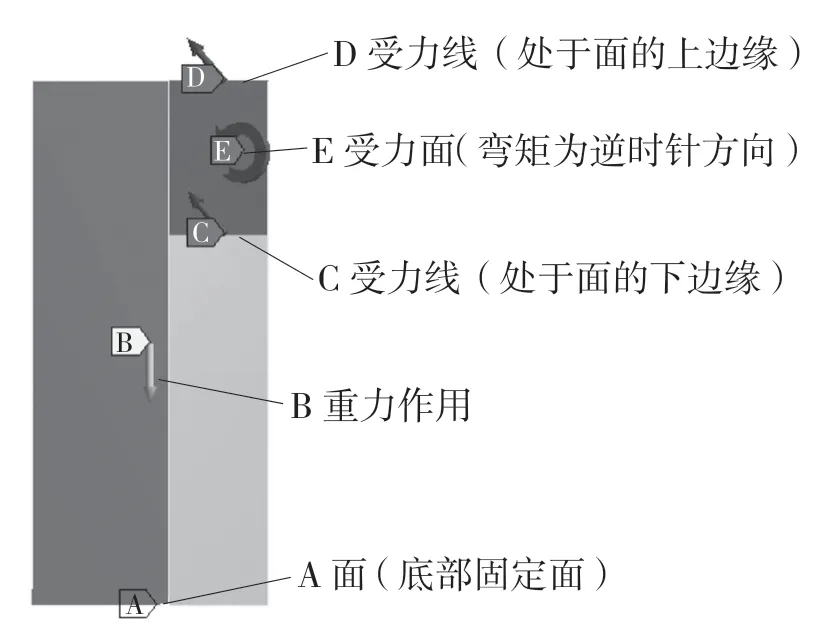
图6 立柱受力情况Fig.6 Stress condition of column

图6 中E 受力面为上工况时主轴箱与立柱的接触面，机床工作时，主轴箱上的力对此面产生弯矩作用，此弯矩如图6 所示，E 受力面添加一个逆时针的弯矩作用。而这个面的受力大小分布可能会不均匀，现对其D 受力线与C 受力线即上下两部分进行探讨，研究两个部分的力大小分布权重关系。

现对D 受力线与C 受力线的权重做比较。原先合力的大小为定值，现改变两者大小比例值，如表2 所示。其中XD/YD 与XC/YC 分别为D 受力线与C 受力线在X 和Y 方向受力大小。

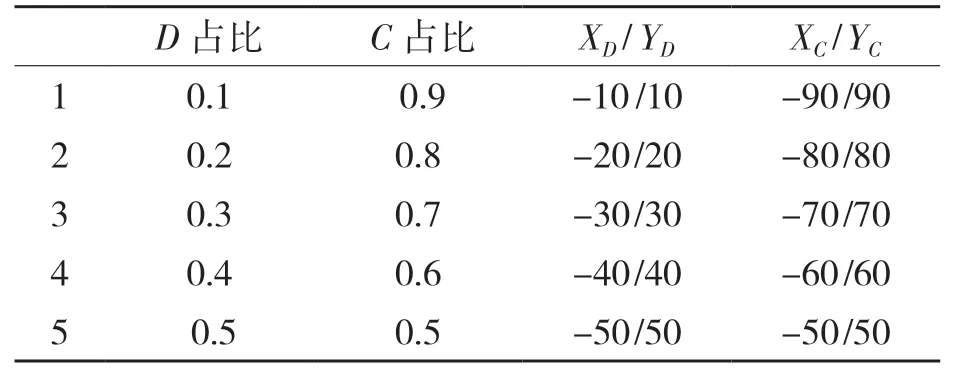
表2 计算外力Tab.2 Calculation of external force

表2 数据中，力的单位为kN。XD/YD与XC/YC力大小的总和为100 kN，现讨论两个部位的力占比情况与拓扑结果做对比，其各个受力大小不同情况拓扑出结果如图7 所示。

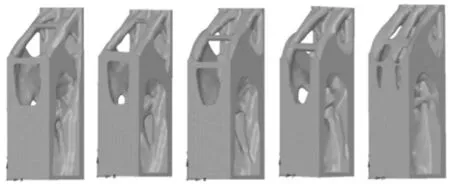
图7 立柱拓扑结果Fig.7 Column topology results

对这5 种拓扑结果分别进行后处理与重新计算其变形情况，其5 种情况最大整体变形如表3所示。

表3 不同情况变形大小Tab.3 Deformation size under different conditions

由其结果可以看出，比例为0.2/0.8 时的变形为0.287 mm，其整体变形量比其他4 种结果变形较小，则此受力比例较其他4 种较优。此拓扑模型的下面线受力更大，上面线的受力较小。经过后处理重新分析此模型，得出应力与整体变形大小，其静应力与整体变形大小如图8 所示。

图8 静应力与变形Fig.8 Static stress and deformation

由结果可知，其最大等效应力为22.64 MPa，整体变形为0.287 18 mm。

对此拓扑模型进行模态分析，可以得出前6阶固有频率，如表4 所示。

表4 前6 阶模态的固有频率Tab.4 Natural frequencies of the first six modes

由表4 可以看出，拓扑模型的一阶固有频率为177.1 Hz。拓扑模型一阶振型由图9 所示。

图9 拓扑模型1 阶振型Fig.9 First mode shape of topological model

3 模型重构

根据立柱拓扑结果初步重构出其模型，如图10 所示。

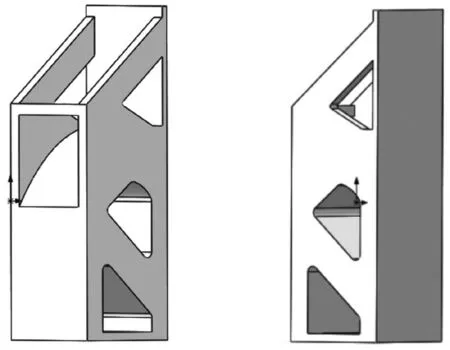
图10 立柱重构模型Fig.10 Column reconstruction model

对重构出的模型重新进行分析，得到其应力、变形与应变，如图11 所示。

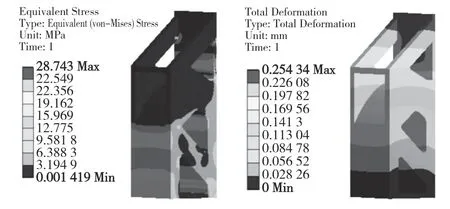
图11 重构模型的应力与变形Fig.11 Stress and deformation of reconstructed model

由重新分析可以得出最大等效应力大小为28.743 MPa，其位于立柱与底座接触结合部右侧；整体变形最大值为0.254 34 mm；应变与应力成正比，大小为0.000 265 64 mm。可以看出整体变形比拓扑结果小，其刚度性能良好。

将重构的模型底面固定后进行模态分析，分析出重构模型的前6 阶固有频率，如表5 所示。

表5 前6 阶模态的固有频率Tab.5 Natural frequencies of the first six modes

由模态分析得出，前6 阶固有频率，其中1阶固有频率为237.3 Hz。重构模型一阶振型如图12 所示。

图12 重构模型1 阶振型Fig.12 The first mode shape of reconstructed model

4 拓扑模型与重构模型模态对比

原始实体模型为149.8 Hz，拓扑模型为177.1 Hz，而重构模型的一阶固有频率为237.2 Hz，可以看出重构模型与拓扑模型的1 阶固有频率都高于原来的拓扑之前的1 阶固有频率。现将拓扑模型与重构模型的前6 阶固有频率进行对比，如图13 所示。

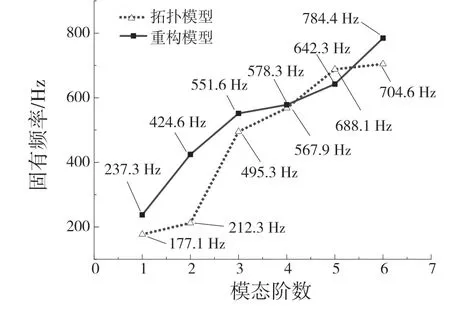
图13 前6 阶模态对比Fig.13 Comparison of the first six modes

重构模型的前6 阶固有频率总体上要略高于拓扑模型的前6 阶固有频率。在机床运转时，最主要看1 阶固有频率的大小，1 阶固有频率越大，那么它在工作时的性能就越好。拓扑模型与重构模型1 阶固有频率都大于原始实体模型的1 阶固有频率，总体上性能得以提升。

5 结论

利用拓扑优化方法探究了立柱结构型与性能，对一个立柱的实体结构进行拓扑，拓扑过程中考虑到多种加工工况，对上中下3 种工况进行拓扑优化，分别得到其构型。对立柱单独优化考虑了力通过主轴箱部分传递给立柱的分布情况，分为5 种情况，最终以变形大小选择较优模型。通过此法得到的模型与多种加工工况得到的模型类比，重构一个模型。将他们的性能对比，发现重构模型与拓扑模型的1阶固有频率都有所提升，重构模型的前6 阶固有频率更好，而且重构模型的总体变形也比拓扑模型的低，则此模型较优。