基于改进Grey-AHP的雷达装备维修性评估方法*

2021-12-28张馨予胡冰张逸楠边志芸

现代防御技术 2021年5期

张馨予，胡冰，张逸楠，边志芸

(1.空军预警学院，湖北武汉 430019;2.中国人民解放军63656部队，新疆和硕 841200；3.中国人民解放军95174部队，湖北武汉 430040)

0 引言

雷达装备维修性是指雷达装备在规定的条件下和规定的时间内，按规定的程序和方法进行维修时，保持或恢复其规定状态的能力[1]。雷达装备维修性评估是在雷达装备寿命周期各阶段，对其维修是否方便、快捷、经济，是否满足维修性指标要求做出的评价[2]。在鉴定定型阶段对雷达样机维修性要求进行评估，其结果可为订购方提供采购依据。

目前，关于维修性评估的研究有了一定成果。在指标体系构建方面，文献[3]建立了基于维修事件的维修性人素工程要求评价指标体系；文献[4]建立了装备维修性定性评价指标体系；文献[5]建立了军用车辆的可靠性、维修性与保障性参数体系。在评估方法的应用上，文献[6]利用云模型算法对某导弹维修性进行评价，文献[7]运用模糊综合评判法对装备维修性设计进行评估，文献[8]利用模糊层次分析法对航空产品维修性进行评价，文献[9]采用基于灰色关联度的模糊综合评价方法对装甲车辆进行维修性评价。而现阶段对装备维修性指标体系的研究，主要根据定性指标构建指标体系，对定量指标考虑较少，围绕设计参数构建指标体系较多，对实测效果考虑较少，且评估对象多为导弹、船舶、航空产品、装甲车辆等，缺少与雷达装备相关的研究。

灰色系统理论(grey-system theory)是以部分信息已知、部分信息未知的贫信息系统为研究对象，对已知信息进行开发、利用，生成有价值的信息[10-11]。层次分析法(analytic hierarchy process，AHP)是一种将定性评价问题定量化处理的决策评价方法[12]。灰色层次分析法将灰色理论和层次分析法结合[13]，利用层次分析法确定层次结构与各层次指标的相对权重，通过灰数和白化函数对指标进行量化比较，有助于提高评价的科学性和精确性[14-18]。

雷达装备维修性评估指标繁杂，存在指标间量纲不一、部分指标量化困难、指标间信息不完整和不确定等现象，导致评估困难。针对以上问题，本文提出了基于改进Grey-AHP的雷达装备维修性评估模型。首先，构建了雷达装备维修性评估指标体系；其次，通过改进的AHP赋权方法对指标赋权；然后与灰色理论相结合，提出了适用于规范雷达指标值的四类函数形式；最后，根据实例给出了3种研制方案的排序结果。采用此模型对雷达装备维修性进行评估，计算简单，能够将定性分析量化处理，且避免了信息丢失,为雷达装备鉴定定型阶段维修性评估提供一种可行方法。

1 雷达装备维修性评估指标体系构建

雷达装备的维修应尽量减少维修停机时间、降低维修难度、提高维修安全性，同时对维修保障资源提出了更严格的约束条件。根据雷达装备维修性要求、结合雷达使用特点，本文从装备设计、维修决策、维修保障等角度考虑，构建了定量指标与定性指标相结合、设计特性与实测效果相结合的指标体系。

雷达装备维修性要求由4个部分组成：管理要求、定量要求、定性要求与维修保障要求。结合维修性的试验与评定、维修保障设计与评定的要求与方法，雷达装备维修性指标体系可归纳为综合参数、设计参数、时间参数和维修资源参数4部分。

维修性综合参数由雷达装备维修性管理要求引出，是雷达装备维修性工作目标的综合体现。主要有年维修器材费(万元)、站级故障修复比(%)等。

维修性设计参数由雷达装备定性要求引出，是体现维修快速、经济而对其设计、工艺及其他方面提出的要求。如可达性、标准化与互换性、故障检测率(%)、模块化、识别标记、人素工程、维修安全性、防差错设施等。

维修时间参数由雷达装备维修性定量要求引出，是体现战备完好性、任务成功性等方面的目标和约束条件。主要有平均修复时间(min)、预防性维修时间(min)、重要部件更换时间(min)、首次翻修期(a)、冗余分系统切换时间(s)等。

维修资源参数由雷达装备维修性维修保障要求引出，是维修保障供应及时、有效的体现。主要有维修人员数质量、技术资料齐套率(%)、备件供应率(%)、维修设备与设施齐套率(%)等。

依据雷达装备维修性要求，构建如图1所示的雷达装备维修性评估指标体系。

图1 雷达装备维修性评估指标体系Fig.1 Radar equipment maintainability evaluation index system

2 AHP赋权与Grey-AHP评估方法

2.1 AHP法计算权重

AHP法确定指标权重的步骤如下：

Step 1 构建递进层次结构。对评估对象进行分析，确定其影响因素。根据因素之间的关系及其归类分成不同的层级。下层因素影响上层因素，相同层的因素之间互不影响，相互独立。

Step 2 构建判断矩阵。假设评估对象A受n个因素{a1,a2,…,an}的影响，按照如表1所示的1～9比例标度法，将2个互异的因素ai和aj(i≠j)对评估对象A的相对重要性进行比较，分别记为aij和aji，得到判断矩阵(aij)n×n。

Step 3 计算各因素权重。计算权重的方法有算数平均法、几何平均法、特征向量法和最小二乘法，传统AHP法在计算权重时仅使用一种方法。

Step 4 一致性检验。计算判断矩阵的最大特征根λmax，根据式(1)计算判断矩阵的一致性指标CI：

(1)

计算一致性比例CR：

(2)

式中：RI为随机一致性指标，其值见表2。当CR=0时，判断矩阵为完全一致性矩阵；当CR≤0.1时，判断矩阵为满意一致性矩阵；当CR>0.1时，判断矩阵不具有一致性，需要对其进行调整，直到其为满意一致性矩阵为止。

表1 比例标度的含义Table 1 Meaning of the proportional scale

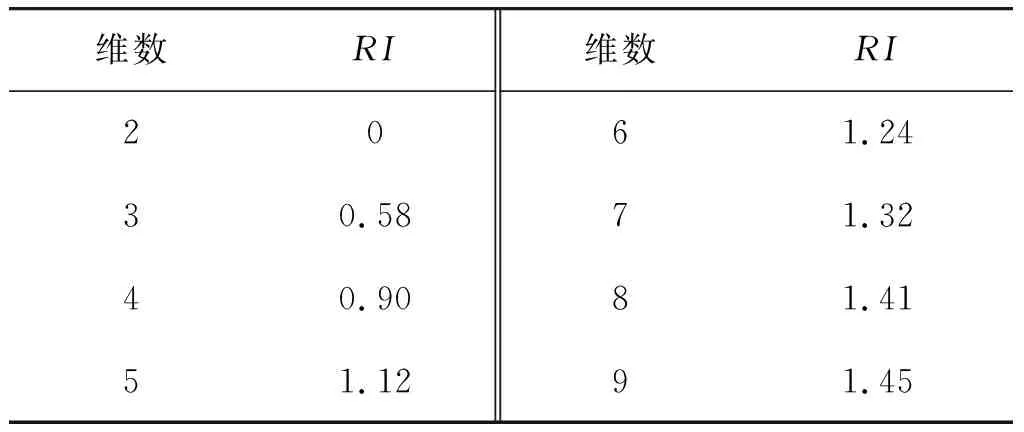
表2 随机一致性指标Table 2 Random consistency index

2.2 Grey-AHP评估方法

Grey-AHP法是灰色系统理论与层次分析法相结合的产物，层次分析法由于仅给出了离散的几个等级关系对评估指标进行量化，直接评估方案导致信息利用不充分，影响评估结果准确性。灰色理论与层次分析法相结合后，利用白化权函数对不同方案进行处理，可以细化方案得分值，提升结果准确性。

Grey-AHP法的步骤如下：

Step 1 建立评估对象的递阶层次结构。应用层次分析法原理，对目标进行逐层分解，使同层次之间的元素其含义互不交叉，相邻上下层元素之间为“父子”关系，形成递阶层次结构。其底层元素即为所求的评估指标。

Step 2 计算评估指标体系底层元素的权重组合。根据前文所述改进的AHP赋权方法，设有N个评估指标，算出底层元素对于目标的权重W=(w1,w2,…,wN)T。

Step 3 求评估指标值矩阵D，设有I个方案，J个指标，则

(3)

式中:dij为方案i中指标j的评估值。

Step 4 确定评估灰类。即要确定评估灰类的等级数K、灰数⊗k以及白化权函数fk，其中，等级数K为评估结果的好坏等级，一般用“优、良、中、差”4个等级衡量，灰数⊗k表示第k个等级对应的白化权函数的函数值变化区间，白化权函数fk为第k个等级对应的白化权函数。针对具体对象，通过定性分析确定。常用的白化权函数有下述3种。

图2中，d1,d2,d3,d4皆为常数，第1级(上)，灰数为⊗∈[0,d1)，函数如图2a)所示；第2级(中)，灰数为⊗∈[0,d2,2d2)，函数如图2b)所示；第3级(下)，灰数为⊗∈[d3,d4)，函数如图2c)所示。白化权函数转折点d1,d2,d3,d4的值称为基本值，可以按照准则或经验用类比的方法获得(客观基本值)；也可从样本矩阵中寻找最大值、最小值和中等值，作为上限、下限和中等的基本值(相对基本值)。

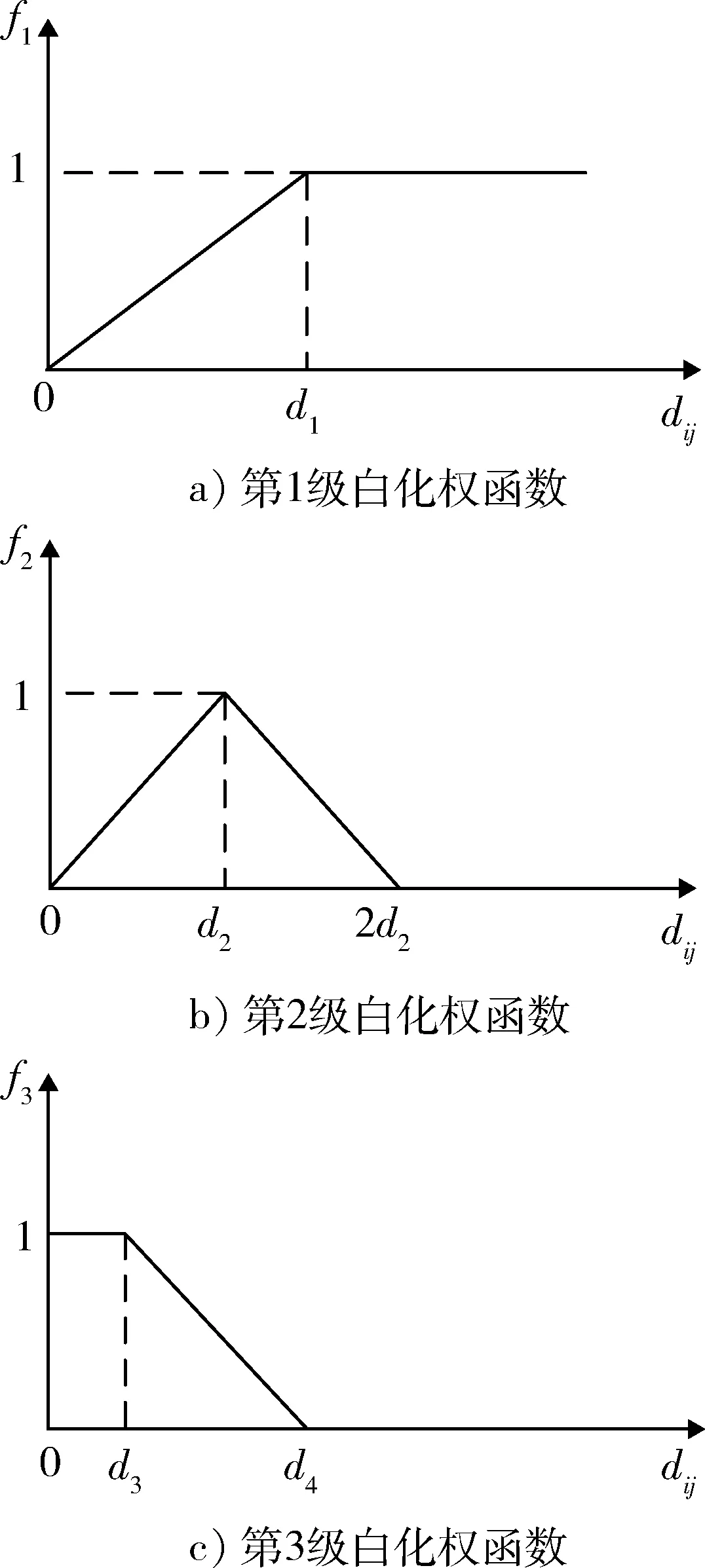
图2 白化权函数Fig.2 Whitenization weight function

设共有K个评估灰类，其中，灰数决定了灰类等级赋值向量Fk，Fk取函数fk中的dk值。

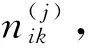
(4)

(5)

(6)

进而可求得方案i的所有指标的灰色评估权矩阵为

(7)

Step 7 进行综合评估。

(1) 综合所有因素，确定方案所属灰类。根据灰类等级赋值向量F=[F1,F2,…,FK]T，可得出方案i综合所有指标后的灰色评估权向量，即

Ri=RiK·F

(8)

(2) 综合所有指标权重，得出方案i的最终排序值

(9)

式中：W为不同指标的权重值。

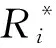
3 改进的AHP赋权与Grey-AHP综合评估

3.1 改进AHP法计算权重

当判断矩阵符合一致性原理时，直接求得判断矩阵的最大特征值对应的特征向量即可作为各指标的权重值。但直接计算传统AHP法对比矩阵的特征值与特征向量计算复杂，采取2种简便方法求矩阵的特征值与特征向量[19]，一种是对判断矩阵的各个列向量求和取平均后再标准化，另一种是对判断矩阵的各个行向量求和取平均后再标准化。以三行三列的矩阵为例进行2种方法的说明。

(1) 对判断矩阵的各个列向量求和取平均后再标准化

设A=[aij],i=j=3为传统AHP法求得的对比矩阵，则有

(10)

式中：W1为一组近似权重。

(2) 对判断矩阵的各个行向量求和取平均后再标准化

设A=[aij],i=j=3为传统Grey-AHP法求得的对比矩阵，则有

(11)

式中：W2为另一组近似权重。

在减少计算量的基础上，2种方法皆可算出与矩阵真实最大特征值对应的特征向量接近的向量作为近似权重值，但1种方法求得的近似权重往往不够精确，本文取2种方法算得的权值近似值的平均值作为最后的权重值，可减小误差，即

(12)

3.2 改进Grey-AHP综合评估

将Grey-AHP中step 4的三类白化函数改为四类白化权函数，使得在对规范化的指标进行灰类评估时更符合雷达装备的固有特性。设K=1,2,3,4，即有4个评估灰类，它们是“优、良、中、差”4级，其相应的灰数及白化权函数如图3所示。

图3 四类白化权函数的具体形式Fig.3 Concrete forms of whitenization weight function

其中，第1类“优”(k=1)，设定灰数⊗1∈[0,0.9)，白化权函数f1，如图3a)所示；

中国储运：请您介绍一下英特诺在中国市场上最受欢迎的产品类型主要有哪些？作为国际上最知名的设备制造和物流整体解决方案提供者，英特诺是在用产品解决方案为客户服务的过程中有哪些经验可以与大家分享？

(13)

第2类“良”(k=2)，设定灰数⊗2∈[0,0.8,1.6)，白化权函数f2，如图3b)所示；

(14)

第3类“中”(k=3)，设定灰数⊗3∈[0,0.6,1.2)，白化权函数f3，如图3c)所示；

(15)

第4类“差”(k=4)，设定灰数⊗4∈[0.1,0.5)，白化权函数f4，如图3d)所示。

(16)

则灰数决定灰类等级赋值向量F=(F1，F2，F3，F4)T=(0.9,0.8,0.6,0.1)T。

在代入白化权函数前，需对评估指标打分值进行规范化，利用式(17)，(18)进行规范化，对于效益型指标，则数值越大越好，此类指标按照式(17)进行处理；对于成本型指标，则数值越小越好，此类指标按照式(18)进行处理，设决策矩阵为Y=(yij)I×J，规范化后的决策矩阵为Z=(zij)I×J,

(17)

(18)

4 实例分析

以某型雷达装备在鉴定定型阶段a,b,c3种方案的维修性评估为例，采用本文提出的改进Grey-AHP法，对各设计方案的雷达装备维修性进行评估。根据图1构建的雷达装备维修性评估指标体系，通过对3种方案的物理样机进行维修性试验，得到如表3所示的各方案雷达装备维修性评估指标值。其中指标C11,C12,C23,C31,C32,C33,C34,C35,C42,C43,C44为定量指标，其指标值可以通过样机试验统计得出，指标C21,C22,C24,C25,C26,C27,C28,C41为定性指标，其指标值为评估者打分的均值。评估者打分时，“1”代表该指标得分极差，“2”代表该指标得分较差，“3”代表该指标得分中等，“4”代表该指标得分较好，“5”代表该指标得分极好。

4.1 改进AHP法确定评估指标权重

评估者根据表1所示的比例标度，对图1中的一级指标B1，B2，B3，B4按顺序进行两两比较，得到判断矩阵：

同理，得出Bk(k=1,2,3,4)所属的二级指标的判断矩阵：

表3 各方案雷达装备维修性评估指标值Table 3 Radar equipment maintainability evaluation index system of 3 schemes

由式(10),(11)可得到2种方法分别求出的近似权重向量:

W1A=(0.087 0,0.470 8,0.206 8,0.235 4),
W2A=(0.091 7,0.480 0,0.179 9,0.248 4),
W1B1=(0.25,0.75),
W2B1=(0.25,0.75),
W1B2=(0.149 0,0.024 4,0.211 9,0.024 4,
0.060 9,0.097 8,0.346 8,0.084 9),
W2B2=(0.130 3,0.025 9,0.201 1,0.025 9,
0.050 4,0.083 8,0.404 4,0.078 7),
W1B3=(0.547 5,0.211 4,0.125 9,0.040 5,0.074 7),
W2B3=(0.589 3，0.185 4，0.112 9，0.043 2，0.069 0)，
W1B4=(0.535 5，0.123 8，0.278 9，0.061 7),
W2B4=(0.572 4，0.119 2，0.245 1，0.063 3),

由式(12)，可求得本文所用的最终权重为

WA=(0.089 4,0.475 4,0.193 4,0.241 9)，
WB1=(0.25,0.75),
WB2=(0.139 7，0.025 1，0.206 5，0.025 1，
0.055 6，0.090 8，0.375 6，0.081 6),
WB3=(0.568 4，0.198 4，0.119 4，0.041 9，0.071 9),
WB4=(0.554 0，0.121 5，0.262 0，0.062 5).

再由精确计算算得矩阵A，B1，B2，B3，B4的真实最大特征值对应的特征向量为

WAtrue=(0.090 4，0.479 8，0.179 1，0.250 7),
WB1true=(0.25,0.75)，
WB2true=(0.127 4,0.024 6,0.199 1,0.024 6,
0.045 6,0.077 8,0.426 7,0.074 1),
WB3true=(0.600 6，0.181 6，0.109 2，0.041 9，0.066 6)，
WB4true=(0.576 3，0.118 5，0.242 9，0.062 3).

由真实的判断矩阵最大特征值对应的特征向量、以上2种方法所得近似权向量及本文方法所得近似权向量对比可见，真实值与本文通过平均值得到的近似权向量值更加接近，且本文所用方法更易于计算。

则各底层指标相对于雷达装备维修性的综合权重：

W=(0.022 4，0.067 1，0.066 4，0.011 9，
0.098 2，0.011 9，0.026 4，0.043 2，0.178 5，
0.038 8，0.109 9，0.038 4，0.023 1，0.008 1，
0.013 9，0.134 0，0.029 4，0.063 4，0.015 1).

4.2 改进Grey-AHP法评估雷达装备维修性

在图1所示的评估指标体系中，指标C12，C21，C22，C23，C24，C25，C26，C27，C28，C34，C42，C43，C44为效益型指标，指标C11，C31，C32，C33，C35，C41为成本型指标。

表3中的数据为决策矩阵Y=(yij)m×n中各元素的值。通过式(17)，(18)对决策矩阵进行规范化后可消除量纲的影响，得到规范化决策矩阵Z=(zij)m×n，为了显示方便，规范化决策矩阵的转置矩阵ZT如下：

按照Grey-AHP法步骤对规范化矩阵进行处理。

(1) 首先计算灰色评估系数、灰色评估权向量及权矩阵。对于评估指标C11，第一个方案属于各灰类的评估系数为

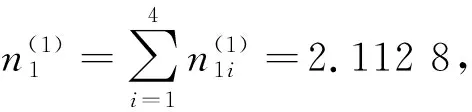
同理可得构成第2,3个方案的所有指标的评估权矩阵R2K，R3K：

(2) 确定方案所属灰类

根据灰类等级赋值向量F=(0.9,0.8,0.6,0.1)T，可得出每个方案综合所有灰类等级后的灰色评估权向量。由式(8)，有

R1=R1K·F=(0.773 6,0.807 1,0.782 6,0.816 0,
0.812 4,0.816 0,0.782 6,0.744 8,0.816 0,
0.744 8,0.816 0,0.782 6,0.816 0,0.816 0,
0.816 0,0.816 0,0.809 0,0.816 0,0.807 1);
R2=R2K·F=(0.816 0,0.816 0,0.816 0,0.816 0,
0.816 0,0.782 6,0.816 0,0.782 6,0.782 6,
0.816 0,0.773 6,0.797 9,0.800 0,0.816 0,
0.758 0,0.758 0,0.816 0,0.788 1,0.816 0);
R3=R3K·F=(0.744 8,0.803 8,0.744 8,0.773 6,
0.816 0,0.782 6,0.816 0,0.816 0,0.744 8,
0.782 6,0.744 8,0.816 0,0.785 6,0.816 0,
0.788 1,0.758 0,0.810 7,0.802 5,0.799 0).

(3) 综合所有指标的权重，给方案排序，根据式(9)，算得