基于马尔可夫模型的多点源诱偏系统作战计算问题*

2021-12-28任义冬金家才罗金亮

现代防御技术 2021年5期

任义冬，金家才，罗金亮

(国防科技大学电子对抗学院，安徽合肥 230037)

0 引言

反辐射武器是遂行压制敌防空体系和摧毁防空雷达的“杀手锏”武器，具有机动性好、突防能力强、效费比和智能化程度高等优点。为有效应对反辐射武器的攻击，防御方常在重要目标周围布设诱饵与目标共同组成多点源诱偏系统。在现代战争中作战计算可为作战指挥提供科学有效的参考依据，为此，研究多点源诱偏系统的作战计算问题对攻防双方都具有重要意义。

当前针对反辐射武器及其对目标的毁伤概率分析[1-4]，以及在诱饵诱偏条件下反辐射武器攻击过程的建模仿真[5-7]，以及诱偏系统抗反辐射攻击[8-12]等问题已有较多的研究，但对反辐射武器攻击多点源诱偏系统时的毁伤概率与兵力计算研究相对较少。

本文针对反辐射武器对多点源诱偏系统的毁伤概率计算问题，提出了基于马尔可夫模型的计算方法，同时根据作战任务要求，可以较好地计算出反辐射武器的兵力需求。防御方可以根据计算结果，相应的优化、修改目标诱饵的布设，从而提高重要目标的生存能力。

1 反辐射武器对单点源的毁伤概率

根据武器战斗部对目标的毁伤机理，毁伤概率可分为两大类：命中毁伤概率和坐标毁伤概率。由于一般的反辐射武器采用以近炸引信为主，触发引信为辅的复合引信，战斗部采用破片杀伤战斗部，故反辐射武器对目标的毁伤概率是坐标毁伤概率。

1.1 相对速度坐标系

在分析反辐射武器对目标的相对运动、瞄准误差或脱靶量时，通常采用相对速度坐标系。相对速度坐标系Oxyz如图1所示，坐标系原点O取在辐射源天线中心处。反辐射武器相对于目标的攻击方向沿x轴方向；z轴平行于水平面；y轴过原点O且垂直于x,z轴，与x,z轴共同组成右手坐标系。

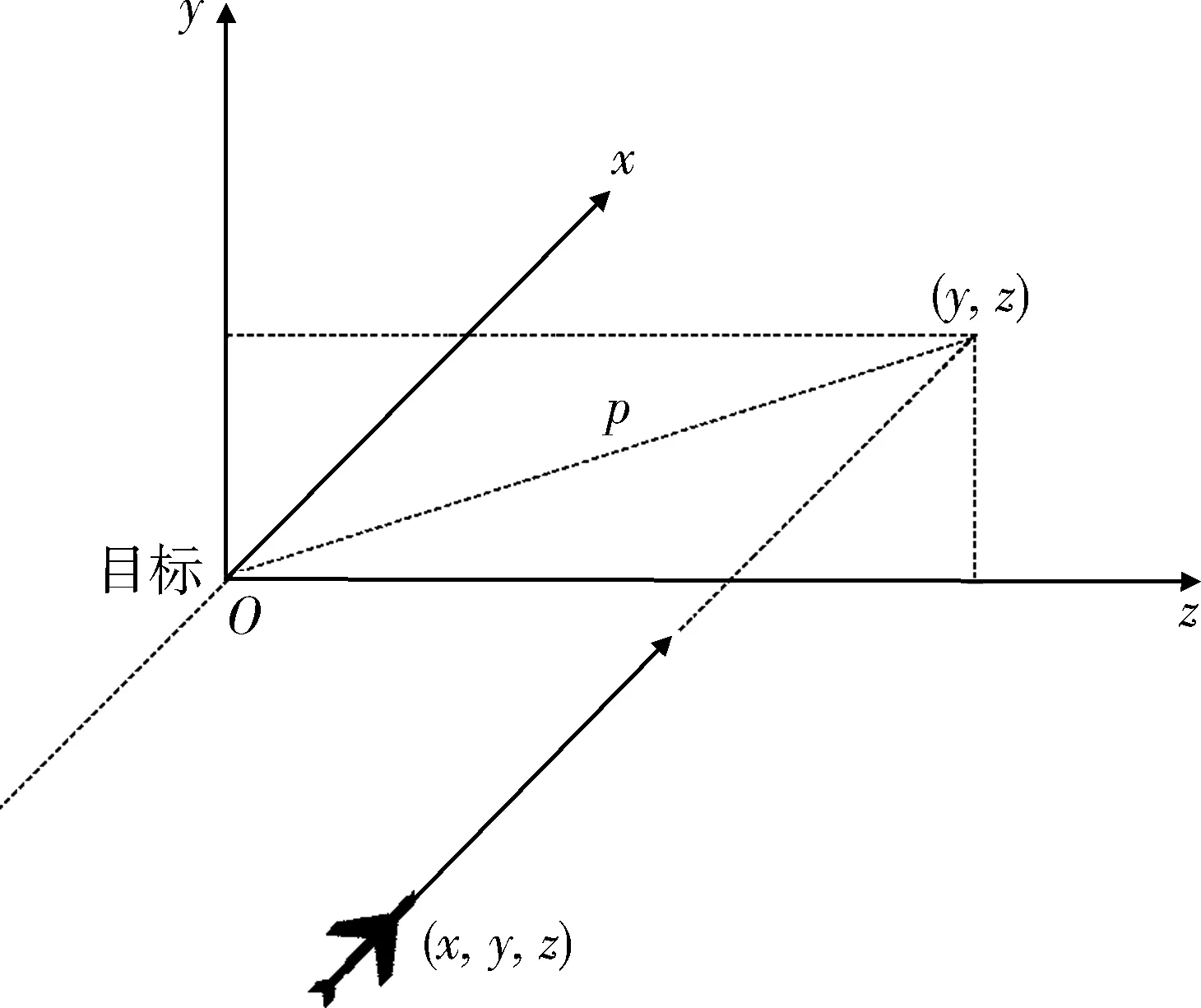
图1 相对速度坐标系Fig.1 Relative velocity coordinate system

1.2 毁伤概率表达式

反辐射武器的战斗部在目标附近爆炸之后，能否毁伤目标与许多因素有关[13-15]：武器系统的制导误差规律fd(y,z)；与制导误差有关的引信引爆概率Φd2(y,z)；引信引爆点沿Ox轴的散布规律φd1(x)；在引信引爆点沿Ox轴的散布规律φd1(x)下，战斗部对目标的毁伤概率Gx。即可得到反辐射武器对单点源的毁伤概率公式为

(1)

其中，

(2)

(3)

(4)

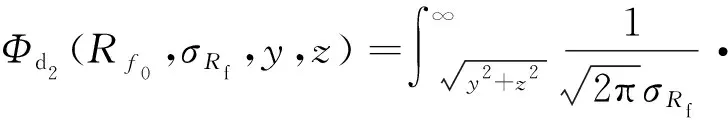
(5)

式中：R为反辐射武器有效毁伤半径；Rf为引信引爆半径；Rf0为引信的平均引爆半径;σRf为引信引爆半径的标准差;mxf为引信引爆点沿x轴散布的平均值;σxf为引信引爆点沿x轴散布的标准差;y0,z0为弹着点y,z的数学期望;σy,σz为标准差。上式(1)可以借助数值积分的方法，利用计算机求解。

2 反辐射武器对多点源的毁伤概率

在多点源诱偏系统中，当反辐射武器被动雷达导引头对目标信号进行搜索时，一般会有多个点源同时在导引头的分辨角内，随着反辐射武器俯冲高度的下降，一部分点源与导引头的张角会逐渐大于导引头分辨角，继而脱离反辐射武器的打击范围。所以可以将反辐射武器对多点源诱偏系统的攻击分为2种情况：①反辐射武器导引头能将所有点源分辨开；②反辐射武器导引头不能将所有点源分辨开。根据此2种情况可分别计算出反辐射武器对目标的毁伤概率，并依据任务要求计算出所需兵力。

2.1 反辐射武器对多点源的瞄准点坐标

当反辐射武器导引头能将所有点源分辨开时。其结果是反辐射武器对多点源诱偏系统中的某一个点源进行打击，则最终对点源的毁伤概率可用单点源的毁伤概率进行计算。由于多点源诱偏系统其诱饵与目标之间的信号特征(如载频、重复频率、脉冲宽度等)、极化方式、发射功率等近似相同，则反辐射武器对各点源的选择是等概率的。

当反辐射武器导引头不能将所有点源分辨开时。其结果是反辐射武器对多点源诱偏系统中最终不能分辨的点源进行打击。在相对速度坐标系下，根据多点源诱偏系统诱偏公式[9]可求得瞄准点的坐标为

(6)

(7)

式中：n为不能分辨的点源数；Emi，Emk为第i,k个点源发射信号在反辐射武器被动雷达导引头处电场强度幅值;(xA，yA，zA)为反辐射武器坐标;(xk，yk，zk)为第k个点源坐标;λk为第k个点源波长;(φi-φk)为第i个和第k个点源辐射信号在反辐射武器被动雷达导引头处的相位差。

在实际系统中，鉴相器输出端、检波器及自动增益控制电路中的低频滤波器，能够滤掉信号中含有cos Δφik因子的全部信号成分。则瞄准点的坐标可化简为

(8)

(9)

当各点源载波近似相同，且各点源在Oyz平面内且距离反辐射武器较远时，瞄准点坐标进一步化简为

(10)

(11)

此即各点源功率质心坐标。当各点源辐射信号在反辐射武器出电场强度幅值近似相等时，可将瞄准点的坐标可化简为

(12)

(13)

即此时反辐射武器的瞄准点坐标为不能分辨的各点源坐标的均值。

2.2 可分辨各点源时的毁伤概率

设目标雷达周围配备了N个诱饵，则目标雷达与诱饵组成了N+1个点源的诱偏系统。M数量的反辐射武器顺序对多点源诱偏系统进行攻击，设状态向量Xn为反辐射武器第n次攻击后诱偏系统的状态，由于反辐射武器第n次攻击后诱偏系统状态Xn的概率完全由状态Xn-1决定，而与之前状态Xn-2，Xn-3，…，X0无关，因此诱偏系统状态的变化是个马尔可夫过程，X0,X1,…,Xn-1,Xn为一个马尔可夫链。

令Pij=P{Xn=j|Xn-1=i}为转移矩阵P的矩阵元，向量Lm=(lm0,lm1，…,lm,N+1)为第m次攻击后系统各状态的概率分布，其中lmi=P{Xm=i,i=0,1,2，…,N+1}。则第m次攻击后系统各状态的概率分布Lm=L0Pm,L0为系统初始状态的概率分布。

当多点源诱偏系统中所有点源均能被分辨时。设Xn=i(i≤N)表示有i个诱饵被击毁且目标雷达未损伤的状态。当目标雷达被击毁时用状态Xn=N+1表示，则状态Xn=N+1为吸收态，即PN+1,N+1=1。在多点源诱偏系统中所有点源均能被分辨的情况下，雷达和诱饵被选中的可能性相等，当系统状态为i时，反辐射武器选中雷达的概率为

(14)

则选中某一诱饵的概率为1-γi。此时，反辐射武器对选中目标的毁伤概率可用单个反辐射武器对单点源目标的毁伤概率进行计算，根据反辐射武器战斗部特性与目标的易损性，确定出反辐射武器对不同目标的有效杀伤半径R,进而求出反辐射武器对雷达和诱饵的毁伤概率α和β。

在系统状态Xn=i时(即有i个诱饵被击毁)，反辐射武器攻击一次后系统状态发生改变，分析一步转移概率可得：

(1) 系统状态Xn=i时，反辐射武器攻击一次后系统状态未发生改变(Xn+1=i)的概率为

Pii=γi(1-α)+(1-γi)(1-β)=
1-γiα-(1-γi)β;

(15)

(2) 系统状态Xn=i时，反辐射武器攻击一次后系统诱饵数增加(Xn+1=i-1)的概率为Pi,i-1=0；

(3) 系统状态Xn=i时，反辐射武器攻击一次后系统诱饵数减少(Xn+1=i+1)的概率为

Pi,i+1=(1-γi)β;

(16)

(4) 系统状态Xn=i时，反辐射武器攻击一次后系统目标雷达被摧毁(Xn+1=N+1)的概率为

Pi,N+1=γiα.

(17)

则一步转移矩阵为

在M批次反辐射武器顺序攻击后，系统各状态的概率分布为LM=L0PM,则目标雷达被摧毁的概率为lM，N+1=P{XM=N+1}。

现设多点源诱骗系统中诱饵数N=2，反辐射武器对雷达和诱饵的有效杀伤半径分别为Rα=2，Rβ=3。σy，σz，y0，z0，mxf，σxf，Rf0，σRf均已由实验给出：σy=1，σz=1，y0=1.5，z0=1.5，mxf=1，σxf=1，Rf0=1，σRf=1，则可计算出反辐射武器对雷达和诱饵的毁伤概率α，β分别为0.426 6，0.563 3。状态转移矩阵P为

系统初始状态的概率分布为L0=(1,0,0,0),即P{X0=0}=1,经运算可得M批次反辐射武器对雷达的毁伤概率,见表1。

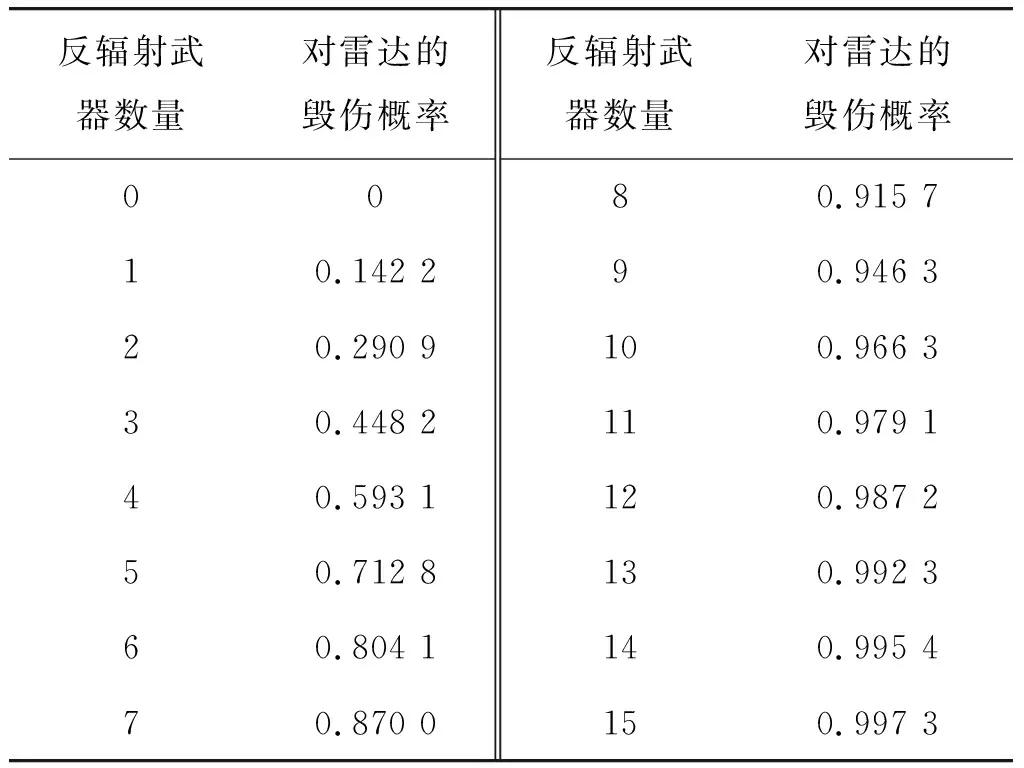
表1 反辐射武器对雷达的毁伤概率Table 1 Damage probability of anti-radiation weapons to radar

反辐射武器对雷达的毁伤概率随反辐射武器数量的变化关系见图2。

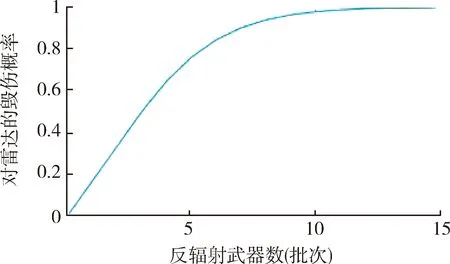
图2 反辐射武器对雷达的毁伤概率Fig.2 Damage probability of anti-radiation weapons to radar

可见当使用6批次反辐射武器时，对目标雷达的毁伤概率可超过80%。当使用12批次反辐射武器时，对目标雷达的毁伤概率可超过98%。

2.3 不可分辨各点源时的毁伤概率

当多点源诱偏系统中多点源不能被分辨时，反辐射武器的瞄准点坐标为各点源坐标的均值。现设目标雷达周围有K个诱饵最终不能被反辐射武器分辨开，则目标雷达与这K个诱饵组成了K+1个点源的诱偏系统。在相对速度坐标系里，令雷达坐标为(0，y0，z0)，第k个诱饵坐标为(0，yk，zk)，反辐射武器坐标为(xA，yA，zA)。

由于在此系统里反辐射武器每次攻击的瞄准点与系统的具体状态有关，即在某一状态下，反辐射武器对各点源的毁伤概率与各点源有关。则此时可对系统按各点源是否被摧毁进行划分，若点源被摧毁则用0表示，若未被摧毁则用1表示，则K+1个点源共有2K+1种状态，用K+1维状态向量S表示各点源的集合，状态向量S最后一个元素表示雷达，1～K个元素分别表示第1～K个诱饵。由于状态向量S每个元素有2种取值0或1。则状态向量S共有2K+1种取值，每个状态向量的取值S(v)(v=1,2，…，2K+1)代表系统的一个状态,则反辐射武器第n次攻击后诱偏系统的状态Xn=S(v)。现令S最后一个元素SK+1=0，即雷达被摧毁时(不论其他诱饵是否被摧毁)的状态为S(2K+1)，当SK+1=1即雷达未被摧毁时的2K种状态依次划分为S(1)，S(2),…,S(2K)，则S(v)(v=1,2,…,2K+1)共有2K+1个取值。例如(1,0,1,0,1,1,…，1)表示雷达未被摧毁的情况下第2个和第4个诱饵被摧毁的状态。当系统处于初始状态时，雷达与诱饵均未被摧毁，即系统状态X0取状态向量(1,1,1,1,…,1)的概率为1，X0取其他状态的概率为0。

在对系统所有状态进行划分后，计算各状态间的转移概率。令Pij=P{Xn=i∣Xn-1=j}为转移矩阵P的矩阵元(这里为表述方便直接用i,j表示S(i),S(j))，向量Lm=(lm1，lm2，…，lm2K+1)为第m次攻击后系统各状态的概率分布，其中lmi=P{Xm=i,i=1,2，…，2K+1}。第m次攻击后系统各状态的概率分布Lm=L0Pm,L0为系统初始状态的概率分布，状态Xn=2K+1为吸收态，则P2K+1,2K+1=1。

当系统状态Xn=S(v)=(1,1,1,1，…，1)时,即所有点源均未被摧毁，反辐射武器的瞄准点坐标(0,Oiy,Oiz)为

(18)

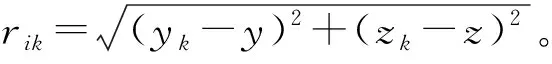
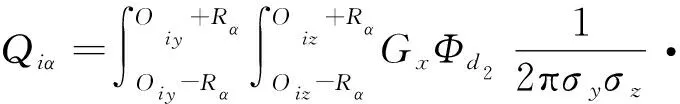
(19)

其中，

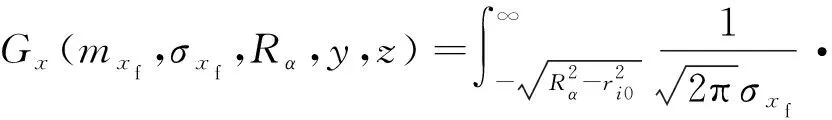
(20)

(21)

对第k个诱饵的毁伤概率为

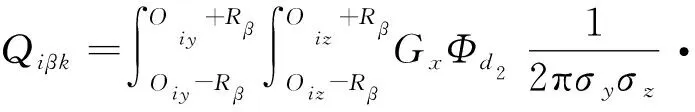
(22)

其中，

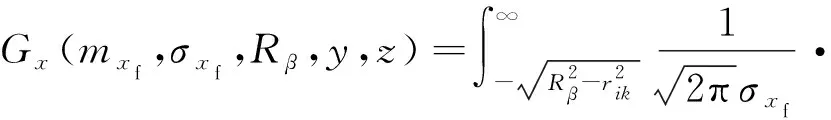
(23)

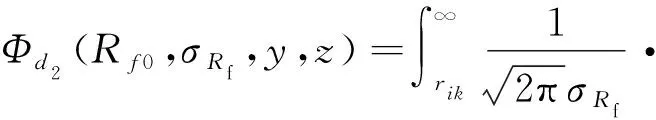
(24)

进一步，可计算出Xn从状态(1,1,1,1，…，1)转移到其他各个状态的概率。例如计算Xn从状态S(i)=(1,1,1,1,…,1)转移到状态S(j)=(1,0,1,0,…,1)的概率Pij，即Xn在各点源均未被摧毁的状态下，经一次反辐射武器攻击后，第2个和第4个诱饵被摧毁的概率。首先分别计算出Qiβ2和Qiβ4，则

(25)

即Pij为雷达未被摧毁的概率、第2个和第4个诱饵被摧毁的概率、其他诱饵未被摧毁的概率的乘积。通过对各状态间的转移概率计算即可得转移概率矩阵P：

根据系统初始各个状态概率分布以及转移概率矩阵，可以计算在M批次反辐射武器顺序攻击后，系统各状态的概率分布LM=L0PM,则目标雷达被摧毁的概率为lM，K+1=P{XM=2K+1}。

现设诱偏系统中不能分辨的诱饵数K=2，其坐标分别为诱饵1(0,0,5)、诱饵2(0,5,0)，雷达坐标为(0,0,0)。此时系统共划分为5种状态即：S(1)雷达与诱饵均未被摧毁的状态(1,1,1)；S(2)雷达和诱饵2未被摧毁而诱饵1被摧毁的状态(0,1,1)；S(3)雷达和诱饵1未被摧毁而诱饵2被摧毁的状态(1,0,1)；S(4)雷达未被摧毁而诱饵1,2均被摧毁的状态(0,0,1)；S(5)雷达被摧毁的状态(X,X,0);其中状态5为吸收态。

设反辐射武器对雷达和诱饵的有效杀伤半径分别为Rα=2，Rβ=3，σy，σz，y0，z0，mxf，σxf，Rf0，σRf均已由实验给出：σy=1，σz=1，y0=1.5，z0=1.5，mxf=1，σxf=1，Rf0=1，σRf=1，则可计算出反辐射武器在各系统状态S(i)下一次攻击对雷达和诱饵的毁伤概率Qiα，Qiβk，从而进一步算出各状态间的转移概率Pij,见表2。

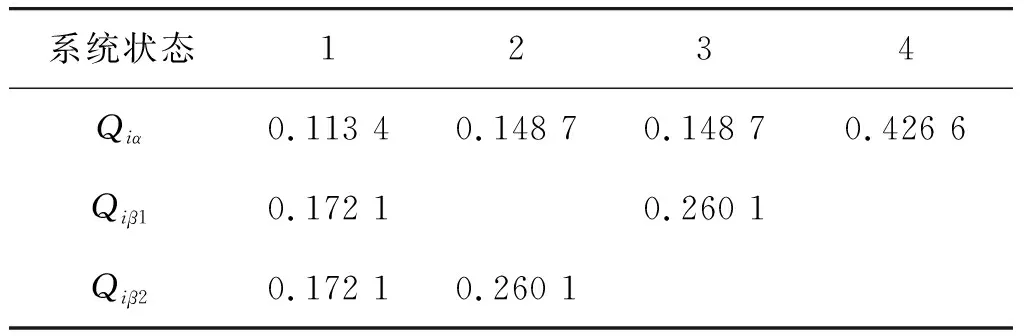
表2 各状态下的毁伤概率Table 2 Damage probability in each state

转移矩阵：

系统初始状态的概率分布L0=(1,0,0,0,0),即P{X0=S(1)}=1,经运算，可得M批次反辐射武器对雷达的毁伤概率，见表3。

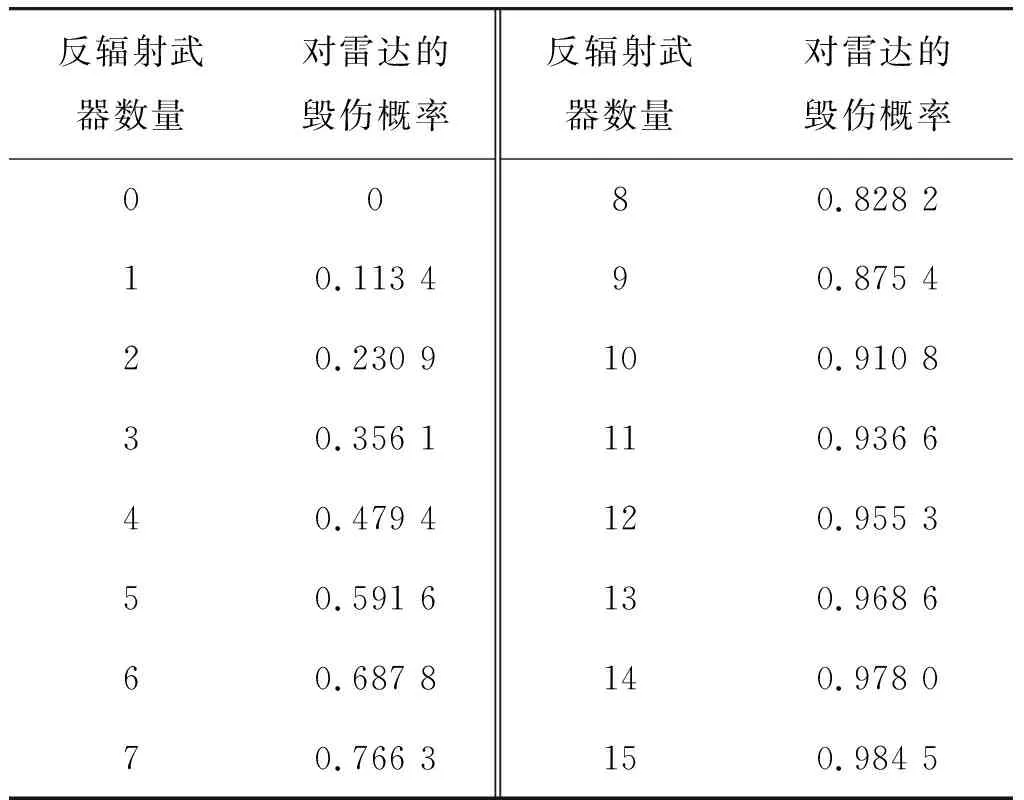
表3 M批次反辐射武器对雷达的毁伤概率Table 3 Damage probability of anti-radiation weapons to radar

反辐射武器对雷达的毁伤概率随反辐射武器数量的变化关系见图3。

图3 M批次反辐射武器对雷达的毁伤概率Fig.3 Damage probability of anti-radiation weapons to radar

可见当使用8批次反辐射武器时，对目标雷达的毁伤概率可超过80%。当使用15批次反辐射武器时，对目标雷达的毁伤概率可超过98%。

由仿真结果可以看出，在给定的参数设置下，当不可分辨各点源时使用同样数量的反辐射武器，一般对雷达的毁伤概率要低于可分辨各点源时的毁伤概率。其原因在于，在给定相同的参数时，对比二者的状态转移矩阵，后者最后一列的矩阵元数值要低于前者，即不可分辨各点源时，各状态经一次反辐射武器打击后，雷达被摧毁的概率较低。