旋转舱体抛罩对其姿态影响的分析*
2021-12-28李维洲宋晓东王帅
李维洲,宋晓东,王帅
(北京理工大学 宇航学院 空间运动模拟与控制实验室,北京 100081)
0 引言
外罩分离是航天器运行过程中经常出现的问题之一,在分离过程中外罩与舱体之间有相互作用力,该作用力会导致分离后航天器本体运动状态改变,因此需要分析外罩与舱体分离后舱体的运动状态。
在航天器的分离问题中,由于自身结构、航天器制造工艺等因素的影响,其质心与设计位置存在一定的偏移,因此航天器分离时会受到由于质心偏移所产生力矩的干扰,从而影响其转动状态[1-3]。此外,物体的柔性变形也会对航天器分离过程产生一定影响[4-5]。针对航天器分离问题,卢丽颖等[6]针对卫星空间二次分离过程,用ADAMS对卫星分离后的姿态进行了定性和定量分析,研究了弹簧刚度等参数对航天器分离速度的影响;张兵[7]等利用ADAMS对三星分离的近场情况进行了计算,并详细分析了各偏差因素对分离过程的影响;李中郢[8]等在以弹簧推杆为分离元件的前提下,建立了船箭分离过程的数学模型,通过仿真计算分析了推杆参数及分散性对飞船入轨精度、入轨安全性及平稳性的影响;舒燕[9]等基于ADAMS建立了包括航天平台、载荷和两类分离机构在内的仿真模型,分析了3种在轨释放、分离载荷方案的分离过程动力学;张华[10]等建立了航天器分离动力学仿真分析模型,进行了航天器分离过程的参数敏感性分析、分离安全包络分析,以此评估分离机构多个设计参数的偏差对航天器分离后姿态的影响;Jeyakumar D[11]建立了卫星的分离动力学模型,在此基础上通过统计方法来计算了指定动态参数的变化。当航天器由大量部件组成时,其释放与分离是一个具有多自由度、含时变约束的多体动力学问题,当多个航天器组成的复杂系统进行释放时需要遵循一定次序,且要保证释放后的航天器彼此之间不碰撞发生危险,基于这一考虑,罗操群[12]等在建立了单个刚体的动力学模型的基础上,利用拉格朗日乘子法获得含连接约束的非线性动力学模型,并以此为基础设计了2种分离释放方案,确保了航天器释放的安全性。
为分析舱体在抛罩后的运动状态以及造成该状态的重要影响因素。本文基于多体动力学理论建立了旋转舱体抛罩过程的含约束动力学模型,其中刚体的旋转姿态由欧拉参数方法描述,时间积分算法采用可精确控制系统能量耗散特性的广义α算法。最后,考虑弹射角、弹射速度、抛罩间隔时间等关键参数,进行了多种工况的计算,得到了相关的计算结果用于指导抛罩分离方案的设计和验证。
1 旋转舱体抛罩分离模型
1.1 旋转舱体模型描述
在旋转舱体抛罩分离模型中,外罩在抛罩前处于收拢状态,该状态下旋转舱体的模型如图1所示。
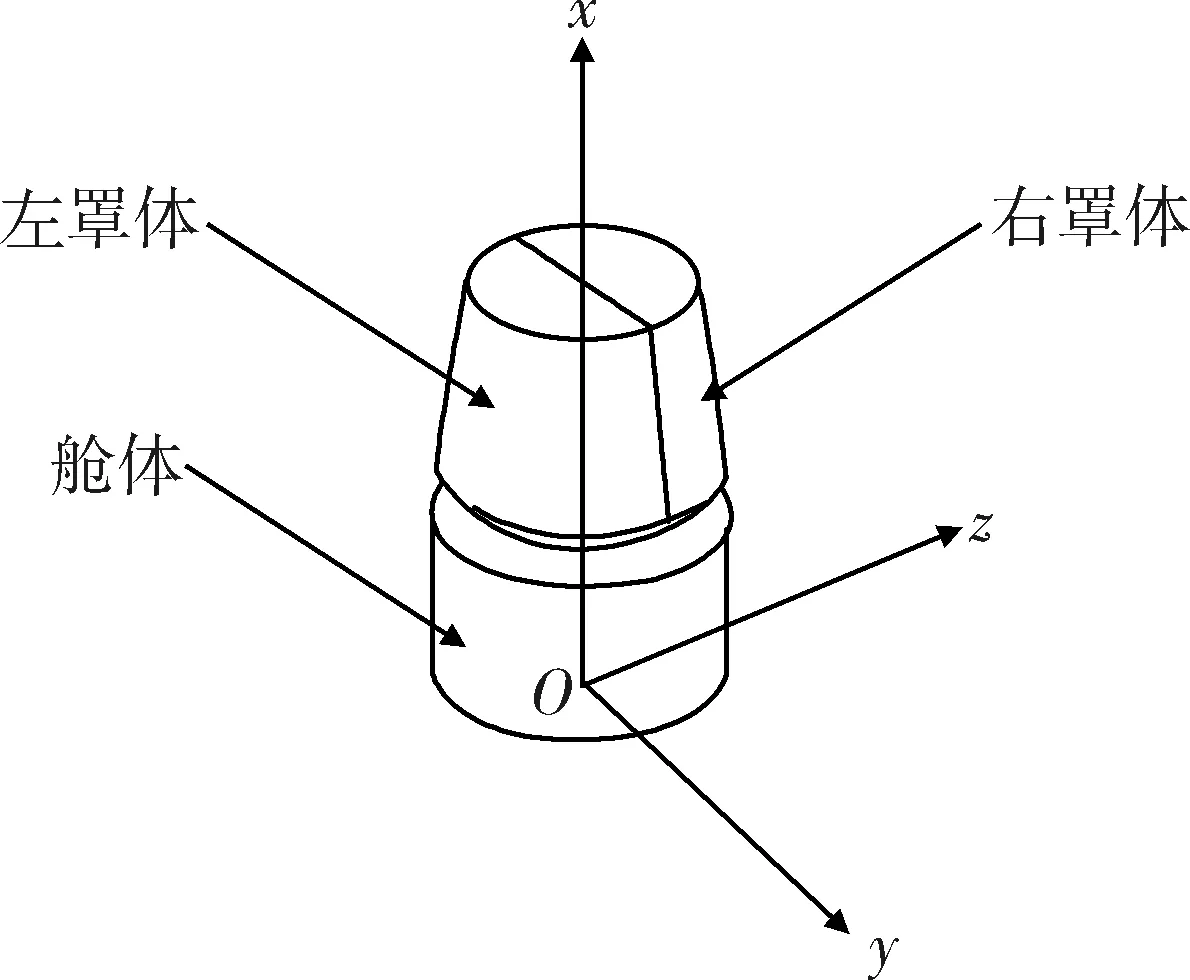
图1 旋转舱体模型Fig.1 Model of rotating cabin
图中坐标系Oxyz为舱体坐标系,坐标系原点为舱体底面中心,Ox轴为舱体回转轴线,Oy位于两罩体贴合面内且与Ox垂直,Oz满足右手坐标系。
模型由左右罩体和舱体3部分组成,在进行动力学建模仅考虑刚体间的相互作用力。舱体为一回转体,罩体分离前与舱体固定连接,此状态下3部分视作整体。其中,两罩体为均质刚体,即两罩体质心位于Oxz平面内。
如图2所示的旋转舱体模型中,整体模型的形心位于Ox轴上,而由于舱体质量分布不均导致整体质心偏离Ox轴一定距离。
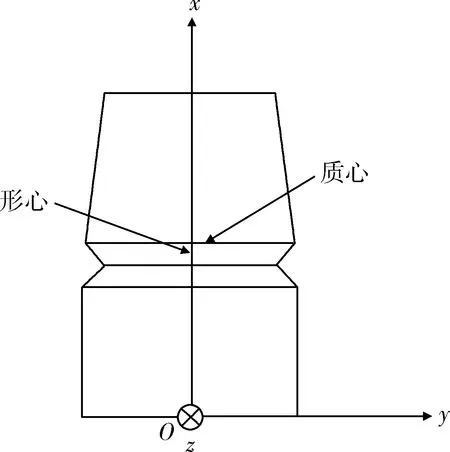
图2 旋转舱体模型质心位置Fig.2 Centroid position of rotating cabin model
1.2 罩体分离方式
在该旋转舱体抛罩分离问题中,由于气囊充气分离时舱体与罩体二者间的作用力十分复杂且时刻变化无法精确表达,但推着罩体逐渐充气膨胀该力逐渐减小,因此在建模时用弹簧力近似代替合力,由于该合力不过质心,因此,分离时该合力对舱体与罩体均有力矩作用。初始时弹簧处于被压缩状态,舱体与两罩体间均固连,罩体与舱体的固定副失效的同时弹簧力开始作用。
如图3所示,弹簧两端分别与舱体和罩体两物体上的固定点相连,两作用力等大反向。

图3 弹簧作用示意Fig.3 Illustration of spring
2 旋转舱体分离动力学模型及算法
2.1 舱体动力学模型建立
如图4建立描述舱体分离过程的相关坐标系。

图4 描述舱体分离过程的坐标系Fig.4 Coordinate system for describing the separation process of cabin
其中坐标系Oxyz为惯性坐标系,坐标系OAxAyAzA,OBxByBzB和O0x0y0z0分别为两罩体和舱体的连体坐标系,其中x轴指向物体纵向惯量主轴方向,z轴与x轴垂直且位于物体的对称平面内,y轴满足右手坐标系。
首先定义用欧拉参数描述的物体旋转参数为
(1)
式中:θ为转动的轴-角表示法中的转动角;n=[n1,n2,n3]为轴-角表示法中的单位旋转向量。
描述刚体姿态的欧拉参数仅有3个独立变量,根据定义有:
(2)
定义
λ=[λ1λ2λ3]T.
(3)
将欧拉参数p写成列矢量形式为
p=[λ0λ1λ2λ3]T=[λ0λT]T.
(4)
由欧拉参数定义的方向余弦矩阵R为

(5)
据此将该式分解得到:
R=EGT,
(6)
式中:
(7)
(8)
据此,在连体基下,刚体角速度矢量可由欧拉参数速度表示为如下的运动学关系:
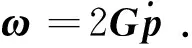
(9)
在惯性基下,刚体角速度矢量则表示为

(10)
连体基和惯性基下的角速度转换关系为

(11)
舱体间依靠弹簧力模拟气囊释放产生的推力,以实现舱体与罩体的分离,以舱体和罩体A为例,弹簧力作用位置如图5所示。
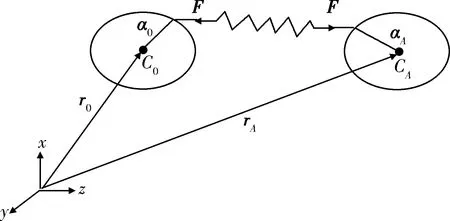
图5 偏心弹簧力Fig.5 Spring force deviating from the center of mass
图中r0,rA为惯性基下两物体质心的位置矢量,a0,aA为质心到弹簧力作用点的位移矢量。设弹簧原长为l0,弹簧刚度为k,弹簧变形后长度矢量l定义如下:
l=(r0+a0)-(rA+aA).
(12)
则据此弹簧力表示为
(13)
式中:l0为弹簧原长;k为弹簧的刚度系数。
由于弹簧力并不过两物体的质心,在计算作用于刚体的广义外力和外力矩时,需要将物体所受弹簧力平移至质心处,平移过后弹簧力会对物体产生额外的力矩。单个分离体的力矢量平移示意图如图6所示。

图6 力矢量平移Fig.6 Translation of force vector
图6中,C为物体质心,a为物体质心指向力作用点的矢量,L为力矢量平移后的附加力矩,根据以上描述有:
(14)
式中:L1,L2均为3×1的列矢量。
由式(9)的变分形式可得
δθ=2Gδp.
(15)
根据虚功原理
δW=L·δθ=(2GTL)Tδp.
(16)
因此,L对应的系统所受广义外力矩为
QL=2GTL.
(17)
经过上述变换后将力矩L由3×1列矢量转换为一个4×1的广义外力矩列矢量。而第i个物体平动所对应的广义外力则无需变换,表示为
QFi=(F1i,F2i,F3i)T.
(18)
因此,第i个物体所受的广义外载荷可写为
Qi=[QFiQLi]T.
(19)
每个刚体的广义外载荷矩阵均可表示为一个7×1列矢量。
该多刚体系统共含有3个刚体,对应的广义外载荷矩阵则可写为
Q=[Q1,Q2,Q3]T.
(20)
在多刚体系统动力学模型中,采用欧拉参数描述转动的第i个刚体的质量矩阵可写为
(21)
式中:
(22)
其中:mi为第i个物体的质量;mipp对应质量矩阵的转动部分,为第i个物体4×4矩阵形式的转动惯量;Ji为第i个物体矩阵形式的转动惯量,
(23)
综上所述,可得到单个无约束刚体的动力学方程为
(24)
以舱体与罩体A为例,在分离模型中,舱体分离前物体间以固定副相连接,如图7所示。
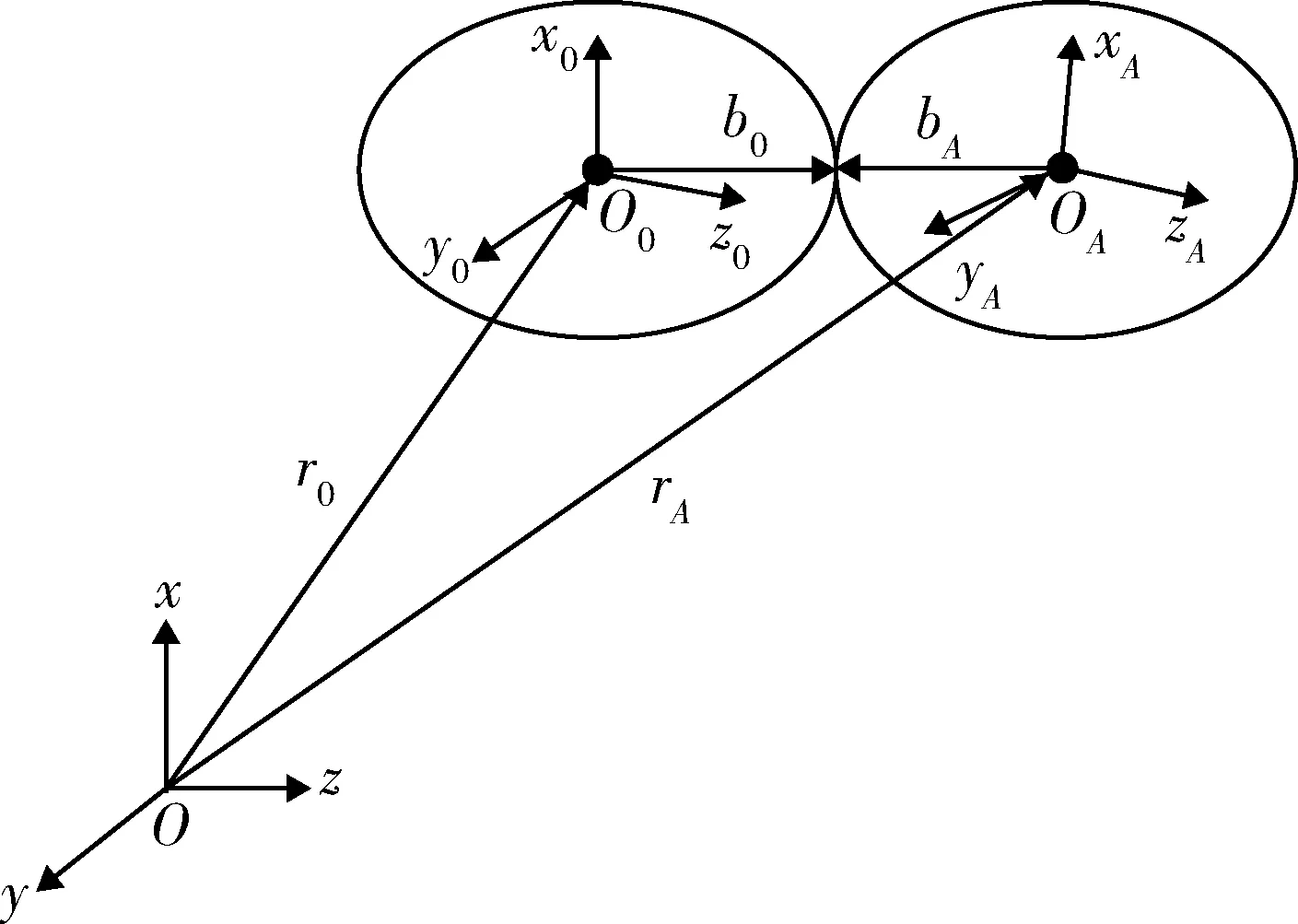
图7 固定连接副在不同坐标下的描述Fig.7 Description of fixed connection pair in different coordinates
在惯性基下,定义u为从惯性基原点到两刚体固接点的矢量,即
(25)
又因为
(26)

因此有
(27)

当刚体以固定副连接时,两刚体的固接位置矢量在全局坐标系中始终重合且描述姿态的欧拉参数始终相等。
因此,两罩体与舱体间的固定副约束方程可写作:
(28)
除上述方程外,每个刚体在运动时其欧拉参数在任意时刻均满足欧拉参数的基本性质,即式(2)。
该多刚体系统由3个刚体组成,系统的总质量矩阵可表示为如下对角形式:
(29)
经过上述推导得出了该多刚体系统的动力学模型,采用拉格朗日乘子法引入相关约束方程后得到描述该多刚体系统动力学状态的微分-代数方程组为
(30)
式中:M为统质量阵;q为系统广义坐标;Φ为系统约束方程;λ为拉格朗日乘子;Q为系统广义外载荷。
2.2 约束多体系统动力学方程求解算法
根据文献[13-15],广义α算法在Newmark算法基础上引入了新的算法矢量a,现采用广义α算法对上述动力学方程进行求解。将上述描述多刚体系统动力学状态的动力学方程在tn+1时刻进行时间离散得到:
(31)
式中:
(32)
其中,h为迭代步长;矢量a参数有如下关系:
(33)
各个参数的选取方法如下:
(34)
式中:ρ∈[0,1]为算法的谱半径,该参数影响算法能量耗散分布的频率范围。针对下一个时间步tn+1,对广义坐标、广义速度、广义加速度和拉格朗日乘子可按如下方式更新:
(35)
(36)
上述公式中的修正项Δq和Δλ由牛顿迭代解非线性方程组得到,可按照如下方法计算:
[ΔqΔλ]T=-J-1bn+1,
(37)
式中:b为残差项,且其计算表达式为
(38)
J为方程关于q和λ的雅各比矩阵:
(39)
3 计算结果与分析
3.1 罩体分离前后对比
罩体分离前后,建立在舱体上的主轴坐标系原点和三主轴方向均有所变化,由于罩体质量远远小于舱体质量,该变化极其微小,但仍然使得原先在坐标系Oxyz的Ox方向角速度在分离后的舱体主轴坐标系Ox0y0z0中的Oy0和Oz0方向有投影,如图8所示。

图8 罩体分离前后的舱体连体坐标系Fig.8 Body-fixed coordinate system before and after cover’s separation
3.2 计算结果
在该计算中,弹簧在开始时即受到压缩,固定副与弹簧同时被释放,弹簧弹力变化趋势如图9所示。
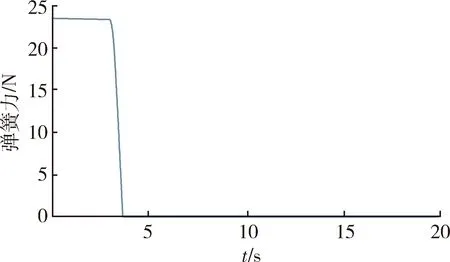
图9 弹簧力曲线Fig.9 Deflection of spring force
罩体分离过程持续时间短暂,约为1 s左右,且弹簧不会被拉伸,即弹簧从压缩状态伸长到原长时弹簧立刻失效,整个过程中弹簧始终保持受压状态。
下文中的波动幅值所表示的是波动的波峰值与中心值之差,转速中心值即转速平均值。
现针对不同初始条件的计算结果如下。
(1) 不同分离速度下的±z方向分离
在图1所描述的坐标系中,±z向分离示意如图10所示。
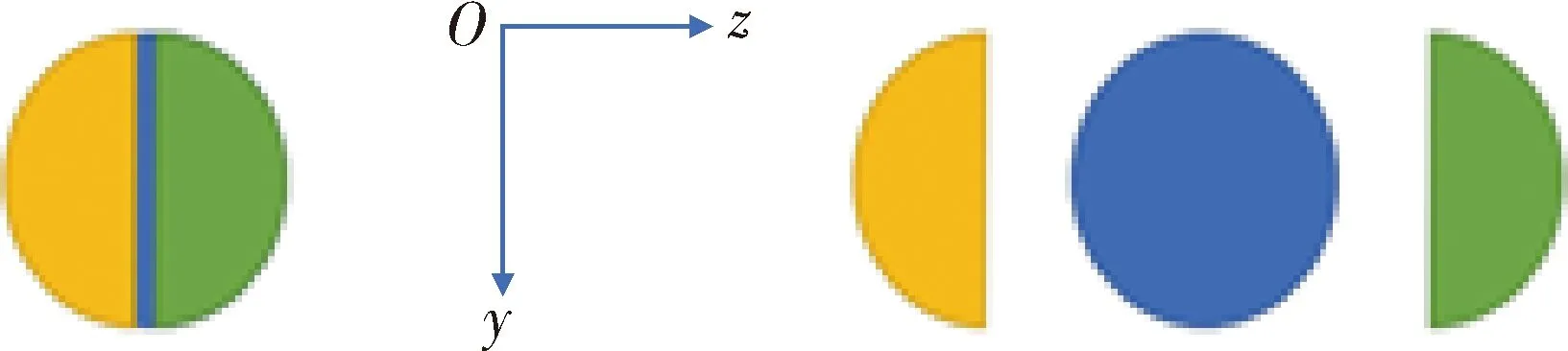
图10 ±z方向分离Fig.10 Separation in ±z direction
在该分离模式下,弹簧弹力矢量位于Oxz平面内且与z轴平行,通过调节弹簧刚度使得罩体以不同的速度飞出。

图11 罩体以不同分离速度在±z向同步 分离时舱体自旋角速度Fig.11 Spin angular velocity of the cabin when the cover is separated synchronously in ±z direction at different separation velocities
从图11中可以看出,增大弹簧刚度时使得罩体以较大速度抛出时,由于弹簧刚度的增加,弹簧力对舱体的力矩也增大,分离后舱体在x方向角速度也越大,而y和z方向分离后变化趋势也基本相同。
此外,对于y和z2个方向而言,当分离时刻该方向的角速度足够小,则后续角速度会在零值附近波动,而x向角速度由于初值过大导致在图中无法看到该波动。
(2) 罩体不同分离时间间隔下在±z方向以2 m/s速度分离
在该分离条件下,第1个罩体分离后,第2个罩体间隔2,4,6 s后再分离。在该分离模式中,当第1个罩体分离后剩余部件质心发生较大移动,惯量主轴方向变化剧烈,而当第2个罩体分离后,质心又移动到距离分离前整体质心位置的不远处。整个分离过程中质心位置移动2次,质心移动趋势如图12所示。

图12 分离过程中的质心位置移动Fig.12 Movement of the center of mass in the separation process
在该分离条件下两罩体分离后舱体的3个方向自旋角速度如图13所示。
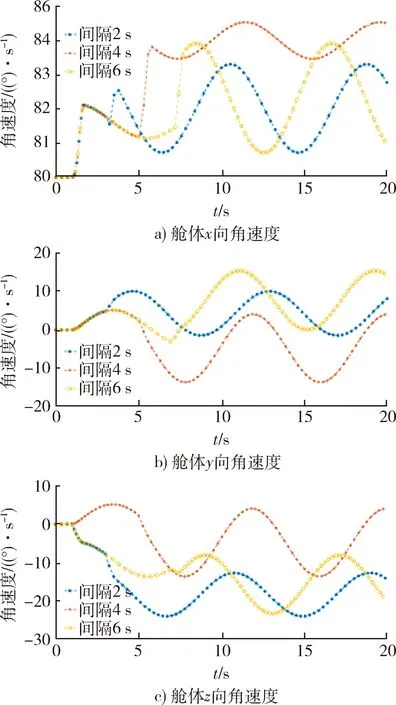
图13 罩体以相同速度在±z向异步 分离时舱体自旋角速度Fig.13 Spin angular velocity of the cabin when the cover is asynchronously separated in ±z direction at the same speed
从图13中可看出异步分离对舱体姿态影响较大,舱体在异步分离时根据当前该方向舱体自旋角速度的不同,在第2个分离且自旋稳定后,舱体3个方向的自旋角速度会呈现较为剧烈的周期性波动。
(3) 罩体以相同速度且同步分离但弹簧力在Oxz面与Oz轴成不同角度
该分离条件下,弹簧力在图1的坐标系中的Oxz面与Oz轴分别成15°,30°,45°,60°,75°和90°夹角,示意图如图14所示。

图14 Oxz面不同角度下的分离Fig.14 Separation at different angles on Oxz plane
不同条件下分离后舱体3个方向角速度如图15 所示。

图15 罩体以相同速度且在Oxz面与Oz轴成 不同角度同步分离时舱体自旋角速度Fig.15 Spin angular velocity of the cabin when cover separates synchronously at the same speed at different angles to Oz axis on Oxz plane
图15a)反应了与Oz轴夹角的大小与x方向角速度的关系,当夹角越大时,分离后对舱体的影响越小,当夹角为90°时,分离后舱体在x方向自旋角速度几乎不变化,但对于另外2个方向却完全相反,针对这2个方向而言,夹角越大分离后该向速度波动越大。
(4) 弹簧力在Oxz面与Oz轴成30°,罩体以2 m/s速度但在不同时间间隔分离
在该分离条件下分离时,舱体3个方向自旋角速度如图16所示。

图16 罩体以相同速度且在Oxz面与Oz轴成 相同角度异步分离时舱体自旋角速度Fig.16 Spin angular velocity of the cabin when cover separates asynchronously at the same speed at the same angles to Oz axis on Oxz plane
从图16中可以发现,在这种有时间间隔的异步分离情况下,分离后x向自旋角速度波动幅值介于0.5 (°)/s(间隔4 s)至1.5 (°)/s(间隔6 s),对比罩体沿±z轴异步分离的情况,两者的波动情况具有很大的相似性,罩体的异步分离会造成飞行器在yz轴上较大的速度波动,其中,间隔2 s分离,yz轴的转速波动幅值约为5 (°)/s,间隔4 s分离,yz轴的转速波动幅值约为8 (°)/s。对比罩体沿±z轴异步分离的情况,两者的波动幅值也基本相当。
(5) 罩体以相同速度且同步分离但弹簧力在Oyz面与Oy轴对称成不同角度
该分离条件下,分离时弹簧力在图1的坐标系中的Oyz面与Oy轴分别对称成15°,30°,45°,60°,75°和90°夹角,示意图如图17所示。

图17 Oyz面对称夹角不同角度下的分离Fig.17 Separation on Oyz plane at different symmetrical angles
在该分离条件下舱体分离后的角速度如图18所示。

图18 罩体以相同速度且在Oyz平面与Oy对称成 不同角度同步分离时舱体自旋角速度Fig.18 Spin angular velocity of the cabin when cover separates synchronously at the same speed at the different symmetrical angles to Oy axis on Oyz plane
通过分析图18可以发现,罩体在Oyz平面内沿+y轴对称打开后同步分离会造成舱体转速下降,且打开角度越大,转速下降越严重,在打开90°情况下,会使x轴平均转速下降到68 (°)/s左右。
罩体在Oyz平面内沿+y轴对称打开后同步分离会造成舱体转速波动,且波动幅值随打开角度的增加略有增加,在打开90°情况下,y轴方向最大角速度能达到-25 (°)/s,而z轴方向则是在打开角度为30°时达到最大角速度25 (°)/s。
罩体在Oyz平面内沿+y轴对称打开后同步分离会造成舱体yz轴整体呈现类周期性章动特点,且随着分离时张角的增大,对yz轴姿态影响整体程增大趋势。15°张角对应章动角速度幅值最小,波动中心值和幅值均约为1 (°)/s;90°张角对应章动角速度y轴幅值约为8 (°)/s、中心值约为-17 (°)/s,z轴幅值约为8 (°)/s、中心值约为6 (°)/s。
(6) 罩体以相同速度但异步分离且弹簧力在Oyz面与Oy轴对称成相同角度
在该分离条件下,罩体分离后舱体的3个方向自旋角速度如图19所示。
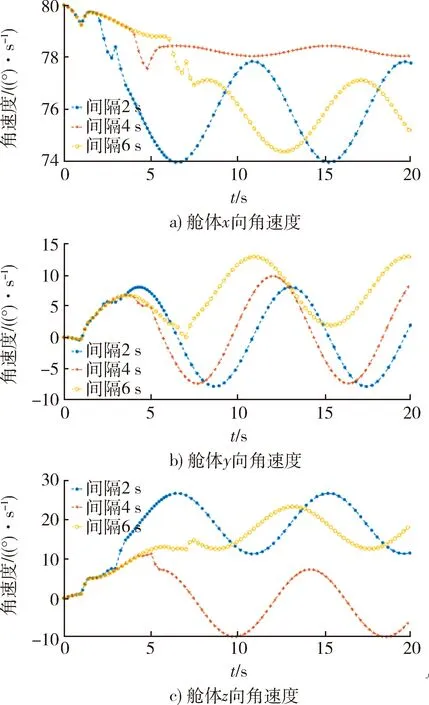
图19 罩体以相同速度且在Oyz平面与Oy对称成 相同角度异步分离时舱体自旋角速度Fig.19 Spin angular velocity of the cabin when cover separates asynchronously at the same speed at the same symmetrical angles to Oy axis on Oyz plane
根据图19分析可以发现罩体在Oyz平面内沿+y轴对称打开30°后异步分离,对舱体的x,y,z3个轴的转速均带来了一定的干扰作用,且均明显大于同步分离的干扰作用。
异步分离,对飞行器的干扰作用,不敏感于分离时间间隔。异步分离对飞行器x轴造成的速度波动幅值在0.5~2 (°)/s;对y轴造成的速度波动幅值在5.5~8.5 (°)/s;对z轴造成的速度波动幅值在5~9 (°)/s。另外异步分离对飞行器yz轴的平均转速中心也造成了明显的影响,其中y轴转速平均值介于0~7 (°)/s,z轴的转速平均值介于-1~17 (°)/s。
(7) 罩体以相同速度且同步分离但弹簧力在Oyz面与Oy轴反对称成不同角度
该分离条件下,分离时弹簧力在图1的坐标系中的Oyz面与Oy轴分别反对称成15°,30°,45°,60°,75°和90°夹角,示意图如图20所示。
图20 Oyz面反对称夹角不同角度下的分离Fig.20 Separation on Oyz plane at different antisymmetrical angles
在图20所示分离条件下,分离后舱体3个方向的自旋角速度如图21所示。

图21 罩体以相同速度且在Oyz平面与Oy反对称 成不同角度同步分离时舱体自旋角速度Fig.21 Spin angular velocity of the cabin when cover separates synchronously at the same speed at the different antisymmetrical angles to Oy axis on Oyz plane
根据图21分析可以发现,罩体的打开过程会带来飞行器自旋速度的下降,且下降幅值与打开角度正相关,打开90°时,自旋速度下降幅值最大,为8 (°)/s。
罩体分离过程会造成舱体自旋速度的上升,且上升幅值与打开角度正相关,打开90°时,自旋速度上升幅值最大,为20 (°)/s,
罩体在Oyz平面内沿+y/-y对向打开一定角度后,以2 m/s的速度同步分离会造成飞行器yz轴产生一定的速度波动,波动幅值在0.5~1.4 (°)/s。
(8) 罩体以相同速度但异步分离且弹簧力在Oyz面与Oy轴反对称成相同角度在该分离条件下,罩体分离后舱体3个方向自旋角速度如图22所示。
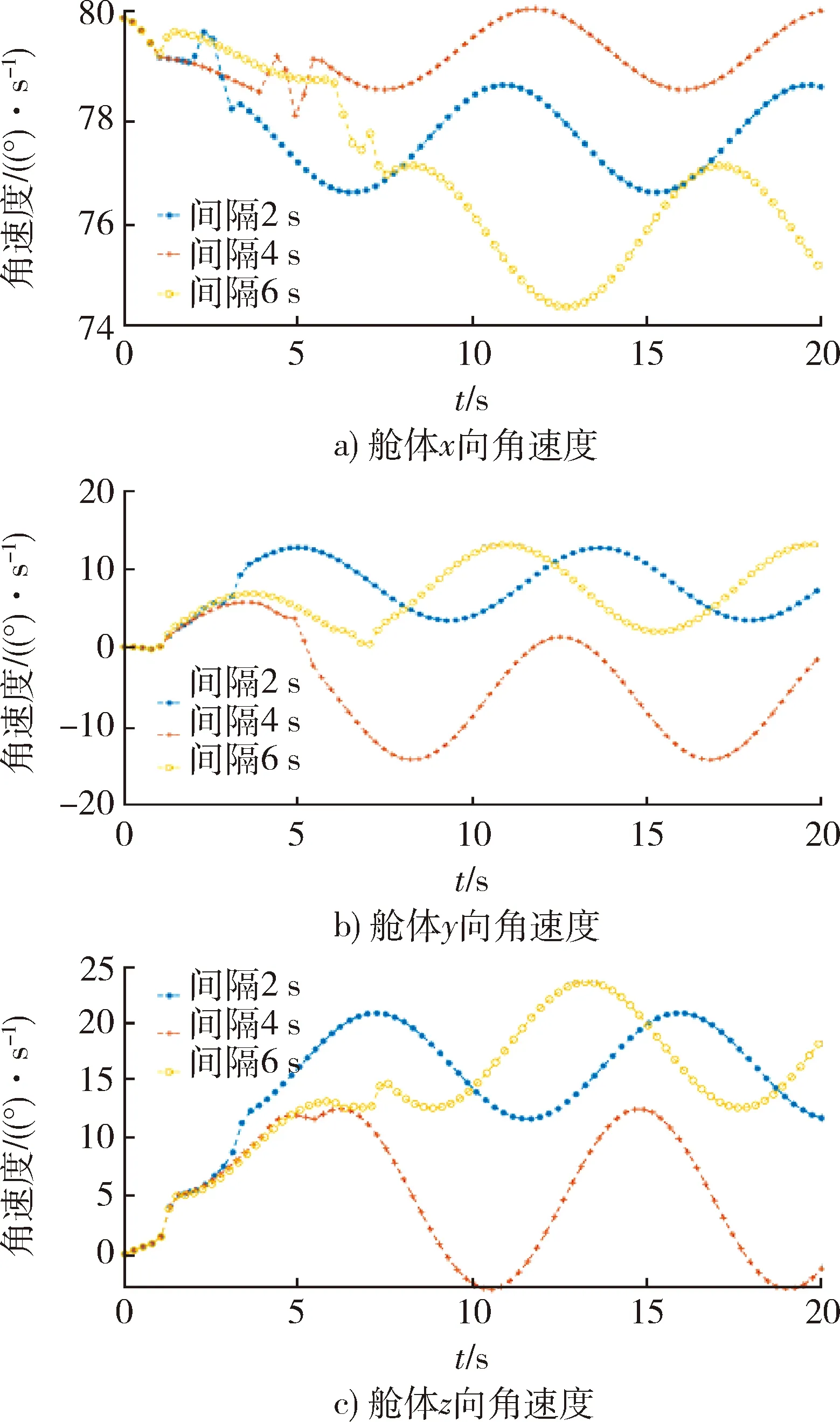
图22 罩体以相同速度且在Oyz平面与Oy反对称 成相同角度异步分离时舱体自旋角速度Fig.22 Spin angular velocity of the cabin when cover separates asynchronously at the same speed at the same antisymmetrical angles to Oy axis on Oyz plane
根据图22分析可以发现异步分离,对舱体的x,y,z3个轴的转速均带来了一定的干扰作用,且均明显大于同步分离的干扰作用。
异步分离对舱体x轴造成的速度波动在0.6~1.2 (°)/s;对Y轴造成的速度波动在5~8 (°)/s;对z轴造成的速度波动在5~8 (°)/s。
异步分离对舱体yz轴的平均转速中心也造成了明显的影响,其中y轴转速平均值介于-7~7 (°)/s,z轴的转速平均值介于5~15 (°)/s。
4 结束语
通过建立旋转舱体的动力学模型,描述了舱体分离过程分离中分离作用力方向、大小以及分离时间间隔对舱体分离这一过程的影响。
质心偏离且处于旋转状态的航天器在空间环境中进行分离时,根据其分离工况的不同,分离后的舱体也会有不同的运动状态。无控状态下的航天器分离后其3个方向角速度必然呈现等周期性的波动,波动幅值与分离时该方向的初始自旋速度有关。为了保证舱体分离后在轴线方向的旋转稳定性,2个罩体需要被同时抛离。且为了使得分离过程二者的罩体和舱体的多次接触碰撞,需要增大作用力使得二者分离过程加快。
通过对舱体分离过程过程的计算分析了相关因素对该过程的影响,为后续分析舱体的运动提供了参考。
