多AUV编队控制
2021-12-27陈世健陈宏丁贺范智艺巩伟杰
陈世健,陈宏,丁贺,范智艺,巩伟杰
(深圳大学 机电与控制工程学院,广东 深圳 518060)
0 引言
现今,自主式水下航行器(AUV)是对神秘海洋探索的重要工具。多AUV系统在水下进行数据采样、环境成像、编队控制和合作围捕等海洋应用领域展现广阔的前景,而水下编队控制是多AUV协调控制策略[1-2]最基础和最重要的研究课题。美国海军研究生院用多AUV协调对水下雷区探测清除[3];刘瑞轩[4]从任务分配和编队控制探讨多AUV的协调控制;许彦营[5]对多AUV的协作提出分布式投标方案。
本文主要研究多AUV基于一致性算法和虚拟领航结构的编队控制,采用一致性算法[6-7]解决位置和姿态的一致性问题,以虚拟领航结构实现预设队形。首先,AUV收集拓扑结构中虚拟领航者信息,得到各类误差值,用一致性算法保持其状态一致;其次,以虚拟领航者位置计算各AUV期望位置,设计时间限定的跟踪控制律,确保各AUV限时内成队。本文使用5个AUV的通信拓扑结构进行编队仿真,验证本文控制策略的可行性。
1 多AUV系统的一致性算法l-φ
在多机器人系统中,将单体AUV的动态概述为
(1)
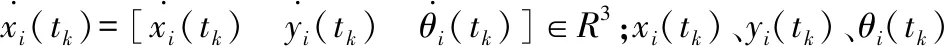
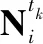
简化式(1),得式(2):
(2)

2 多AUV编队控制系统的设计
建立xwOwyw世界坐标系、虚拟领航者本体xaOya坐标系如图1所示。
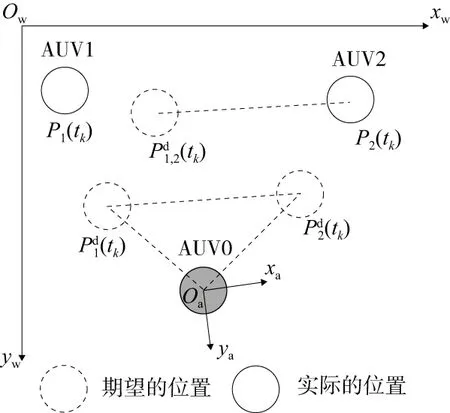
图1 编队控制
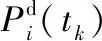
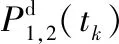
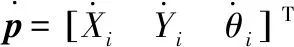
(3)
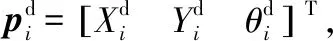
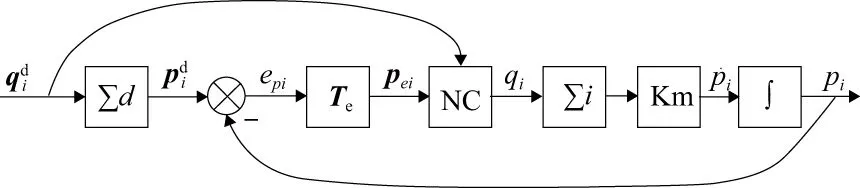
图2 轨迹跟踪控制
图2中:NC为非线性控制系统;∑i为AUV(i)运动学系统;Km为速度角速度限制器,避免过大的线速度和角速度,导致漂移现象。参考系统∑d的运动学方程为
可将机器人AUV(i)在xwOwyw坐标系下的位姿误差定义为
(4)
该式表示机器人AUV(i)从xaOaya坐标系到xwOwyw坐标系的转换,Te是转换矩阵。对式(4)进行求导,得到误差的动力学方程如下:
(5)
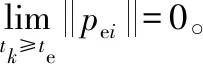
3 轨迹跟踪控制器设计
此系统的特征:假设初始态为x(0)≠0,有状态x(t),系统于有限时间tx内,让x(t)=0。此外,得tx=-ln[ξ2/(ξ2-ξ1x0sgn(x))]/ξ1。
AUV轨迹跟踪控制器设计的步骤如下:
1)针对式(4)的偏航角误差状态θei,设计其一阶系统限定时间约束的控制器:
(6)
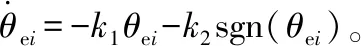
2)对位置误差状态(xei,yei)构成的系统进行位置控制器设计。
借由该引理,可令vi的控制率表示成
(7)
其中:k3、k4>0;0 <β1<1;β2=2β1/(1+β1)。由此可得,系统的闭环形式为
(8)
因此新得到的式(8),能在有限的时间内,使得xei→ 0,yei→ 0。
4 数值仿真
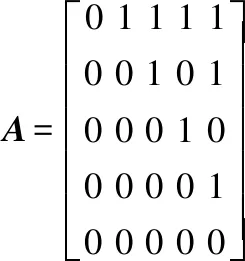
假设某海域有5个AUV,用矩阵A表示AUV间通信网络拓扑图,第1 ~n-1行为跟随者的相互间通信状况,n行为虚拟领航者,无需主动去与其他AUV通信。邻接权重K的设值与A有关,若能与领航者通信,则较大权重在与领航者之间;若与领航者失联,则就近搜索其他AUV获取位置信息,并加大相对于该AUV位置的权重。
4.1 定点编队
设定仿真步长 ΔT=0.02 s,仿真时间5 s。预设在4 s内,5个AUV的预定状态达到一致,形成了预想的编队形状。
设跟随者AUV在xwOwyw坐标系下的初始位姿分别为 (70,70,-π/6)、(200,160,2π/3)、(200,300,π/4)、(450,400,-π/4),虚拟领航者AUV的初始位姿为 (550,300,π/2)、初始角速度为(π/6)rad/s、线速度为0.5 m/s。仿真开始后,各AUV跟踪轨迹路线如图3所示,空心圆为各AUV的初始位置,大圆点为虚拟领航者,灰色为跟随者,浅灰色为各AUV的轨迹。
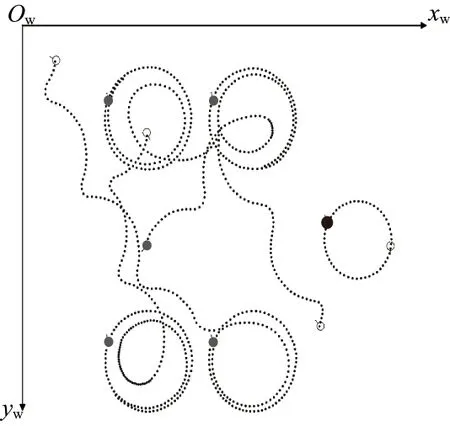
图3 定点编队路线图
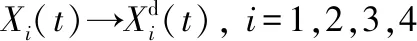
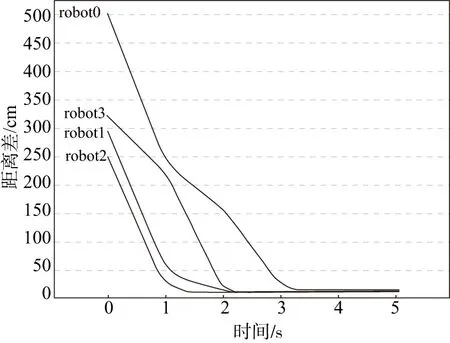
图4 定点编队位置误差图
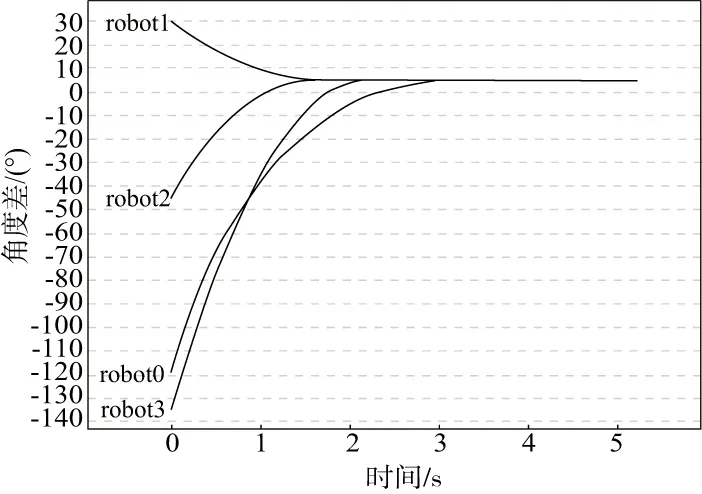
图5 定点编队偏航角误差图
4.2 横排编队
设定仿真步长 ΔT=0.02 s,仿真时间5 s。预设在5 s内,使得5个AUV的预定状态达到一致,形成了预想的编队形状。
设各AUV的初始值,4个跟随者AUV在xwOwyw坐标系下的初始位姿分别为 (40,50,-π/6)、(50,120,2π/3)、(300,130,π/4)、(500,60,-π/4),限速5 m/s。虚拟领航者AUV的初始位姿为 (250,100,π/2)、初始角速度为0 rad/s和线速度0.5 m/s,中间段做正弦移动,再恢复直线。仿真开始后,各AUV的跟踪轨迹路线如图6所示,空心圆为各AUV的初始位置,大圆点为虚拟领航者,灰色为跟随者,浅灰色为各AUV的轨迹。
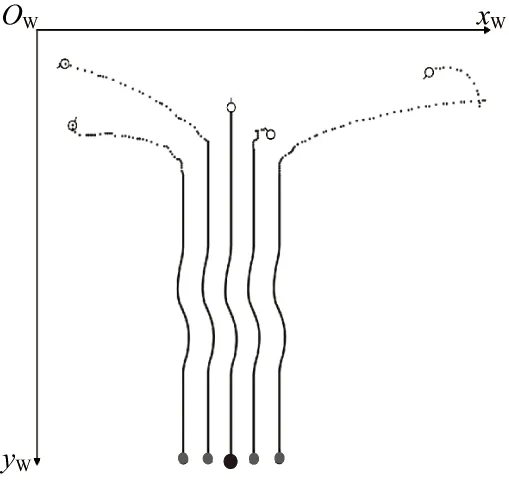
图6 横排编队路线图
由图7-图8知,队形在2 ~ 3 s间完成编队,4个AUV通过网络拓扑结构获取位置信息,与以虚拟领航者为参考的几何位置及角度保持一致。同时,中间队形变换未造成太大影响。由此可知在控制律调解下,AUV(i)在有限时间内跟踪上预设期望轨迹,完成横排队形移动控制。
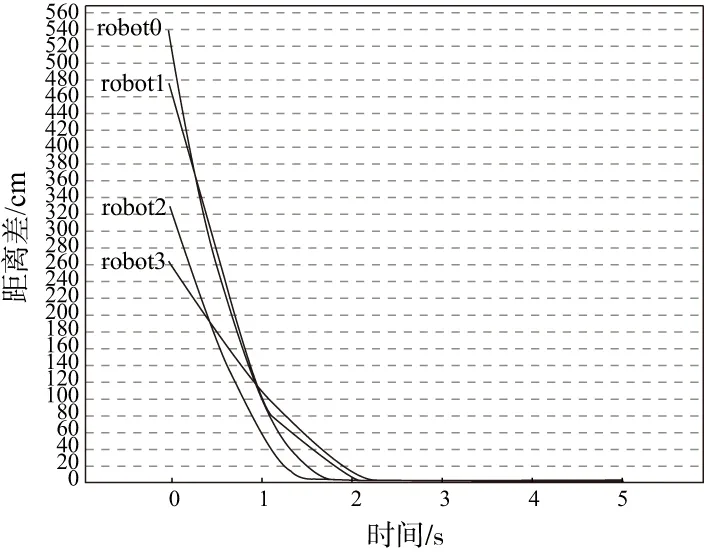
图7 横排编队位置误差图
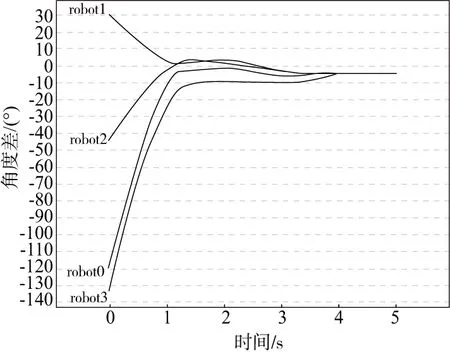
图8 横排编队偏航角误差图
5 结语
本文针对二维平面内多AUV控制系统的编队问题进行研究,选用渐近一致性算法和虚拟领航结构法来解决问题,完成了定点编队及横排编队控制,验证了控制策略的可行性。将本课题研究的控制器应用到多AUV系统在三维的6自由度编队是今后的研究重点。
