立式蜗壳泵轴承-转子系统瞬态动力学响应研究

刘 栋，刘子凌，张亚玲，王颖泽

（江苏大学 能源与动力工程学院，江苏镇江 212013）

0 引言

大型立式蜗壳泵普遍存在振动大、噪声高的问题，转子-轴承系统作为泵的核心部件，是确保泵稳定运行的关键[1-2]。立式蜗壳泵的稳定运行与转子-轴承耦合系统的工作状态密切相关，如导轴承油膜力、转子振幅、变形等[3-4]。分析大型立式蜗壳泵的轴承-转子系统的动力学特性十分必要。

目前，在导轴承静特性研究方面，王鹏朝对可倾瓦轴承的油膜进行分析，研究了进油压力、转速等对油膜压力分布的影响[5]。XIE 等[6]考虑了油膜和轴瓦的相互作用，通过流固耦合对核主泵内第一回路水导轴承进行分析，研究了转速、偏心率、油膜厚度等对油膜压力分布的影响。

在轴承-转子系统的振动、轴心轨迹、动特性系数等方面，XIE等[7]计算了轴承-转子系统固有频率及振型并分析关键点振动幅度，研究了轴承结构参数对转子稳定性的影响。SHI等[8]建立了考虑非线性油膜力的转子模型，通过数值分析研究了转子不平衡量、间隙、轴承长度对轴心轨迹的影响规律。刘杨等[9]基于非线性有限元方法，验证了滑动轴承油膜力模型的准确性，结果表明振动频率以高倍频为主频，油膜振荡特征表现出滞后特征。李元生等[10]提出动态求解方法，研究了轴承间隙和长度、润滑油黏度对滑动轴承动力系数的影响。

在泵的轴承-转子系统稳定性研究方面，蒋小平建立了高压多级泵转子有限元模型，根据坎贝尔条件求解水润滑轴承的动特性系数，通过临界转速、对数衰减率、突加激励下的瞬态响应确定水润滑轴承-转子系统是稳定的刚性系统[11-12]。余四平分析了高速离心泵径向滑动轴承静、动特性，从转子-轴承简化模型的失稳转速变化角度对其稳定性进行了分析[13]。冯琦[14]对多级泵转子系统进行瞬态计算，结果表明了口环密封力能增强转子稳定性。胡倩澜[15]建立了反渗透海水淡化高压泵的转子模型，计算了转子系统的临界转速，结果表明随着叶轮级数增加，转子系统临界转速降低。

目前，与泵的轴承-转子系统动力学分析相关的研究，通常不考虑径向力的变化，有关径向力脉动对泵转子运行稳定性的研究较少。针对上述问题，本文利用数值模拟计算了叶轮内流体的激励力，建立了泵的轴承-转子模型，对“湿态”下轴承-转子系统进行瞬态计算，获得轴承的油膜压力分布的变化规律，计算轴承与叶轮处的振动位移，分析轴承性能与立式蜗壳泵转子系统运行状态，相关研究将有助于提升立式蜗壳泵的运行稳定性。

1 立式蜗壳泵轴承-转子系统模型

1.1 导轴承油膜力模型

1.2 立式蜗壳泵转子模型

本文研究的立式蜗壳泵为双支承悬臂结构，转子结构主要包括叶轮和泵轴两部分，泵轴总长2 339 mm，轴承跨距750 mm。转子系统的实体模型如图1所示，一维梁单元模型如图2所示。

图1 立式蜗壳泵转子三维模型Fig.1 3D model of vertical volute pump rotor

采用COMSOL软件的“梁转子与液体动压轴承”模块对立式蜗壳泵轴承-转子系统模拟计算。将泵轴离散为9个节点，8个轴段单元。根据转子轴径大小设置转子横截面，泵轴材料为40Cr，杨氏模量为2.11×1011N/m，泊松比为0.277，密度为7.87×103kg/m3。叶轮位于节点1处，质量为2 142 kg，直径惯性矩为 341.94 kg·m3，极惯性矩为555.33 kg·m3，质心偏心距为 1×10-5m。导轴承位于节点5处，导轴承主要参数见表1。滚动轴承位于节点7处，其刚度为3.92×109N/m，阻尼为4.42×105N·s/m。

表1 导轴承主要参数Tab.1 Main parameters of guide bearing

2 立式蜗壳泵转子系统瞬态响应分析

2.1 径向力计算

泵在运行过程中，叶轮径向力波动的主要原因是动静干涉作用[17]。为掌握不同工况下叶轮承受力分布规律，本文通过计算泵内部流场，获得了不同工况下的径向力分布如图3所示。不同工况下的叶轮径向力均呈现出5个峰值，每个峰值都在叶片经过隔舌时产生。对比单、双蜗壳泵的径向力可以看出，双蜗壳结构显著地减小了径向力。当偏离设计工况点时，叶轮所受的径向力显著增大，0.6Q工况下的径向力是设计工况的10倍。

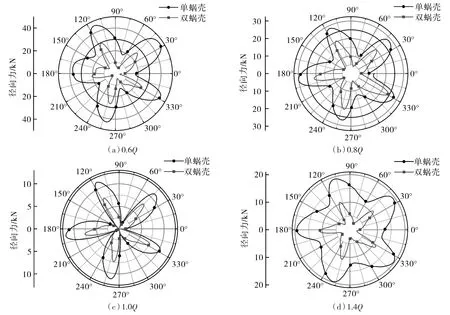
图3 不同工况下径向力分布Fig.3 Radial force distribution under different working conditions

2.2 轴承-转子系统瞬态响应分析

为研究蜗壳结构对转子系统振动特性的影响，本文将叶轮所受的径向力加载到转子系统上进行瞬态响应计算。轴承振动峰对峰值的计算结果见表2，随着偏离设计工况，轴承振动峰对峰值逐渐增加。设计工况下，双蜗壳模型泵的轴承振动峰对峰值为24.93 μm；0.6Q工况时振动峰对峰值最大，数值为91.84 μm。与单蜗壳相比，双蜗壳在各个工况下振动峰对峰值均明显减小，尤其远离设计工况的0.6Q和1.4Q下，振动峰对峰值分别降低了60.12，61.11 μm。根据API610标准，立式泵在轴承处振动峰对峰值应小于100 μm，表2计算结果表明，单蜗壳立式蜗壳泵在0.6Q，0.8Q和1.4Q工况下，振动峰对峰值已经超出标准规定数值。采用双蜗壳结构后，本文研究的4个工况均满足API标准的要求。

表2 轴承振动峰对峰值对比Tab.2 Comparison of bearing vibration peak to peak value mm

表3，4分别为不同工况下叶轮振动的峰对峰值和总位移最大值。双蜗壳模型在叶轮处振动峰对峰值明显小于单蜗壳模型的计算结果，越偏离设计工况点，2个模型的计算差异越明显，在0.6Q工况下，两者差值为0.261 mm。叶轮的总位移最大值表示了叶轮的偏心程度，不论采用单蜗壳还是双蜗壳，在0.6Q工况下，叶轮的总位移值均大于其他工况。与单蜗壳相比，各个工况下，双蜗壳泵的叶轮总位移最大值都明显减小，在0.6Q和1.4Q下减小最显著，分别减小了15.2%和37.8%。

表3 叶轮处振动峰对峰值对比Tab.3 Comparison of vibration peak to peak value on impeller mm

表4 叶轮处总位移最大值对比Tab.4 Comparison of the maximum total displacement of impeller mm

2.3 轴承-转子瞬态响应分析

图4示出不同工况下，双蜗壳模型的轴承-转子系统在导轴承处的位移响应，由图可以看出，Y，Z方向振动位移呈现出周期性变化规律，由于油膜的半速涡动，导致2个方向上的振动周期是转子旋转周期的2倍。各个工况下，Y与Z方向峰对峰值不同，流量从0.6Q至1.4Q变化时，单方向峰对峰最大值分别为 91.84，79.08，24.93，43.96 μm。由此可见，峰对峰值的大小与径向力密切相关。

图4 轴承-转子系统在导轴承处的位移响应Fig.4 Displacement response of bearing-rotor system at the guide bearing

随着偏离设计工况，振动的峰对峰值增大。由于0.6Q工况下叶轮承受的径向力较大且分布不规则，导致轴承处的轴心轨迹非常紊乱，出现转子-轴承系统运行不稳定的现象。对比其他工况，轴心轨迹在设计工况下最稳定，径向振动位移最小、幅值最小。偏离设计工况越多，轴心轨迹越不稳定，径向振动位移越大、幅值越大。除0.6Q以外工况下的轴心轨迹呈现内外五角形状，出现10个峰值，因为叶轮承受的径向力在一个旋转周期内出现了5个峰值，轴心轨迹振动幅值对应径向力的峰值。由于径向力达到峰值，致使轴心偏移量变大，使得单侧油膜变薄，轴承油膜的承载力增大。

图5示出不同工况下，转子系统在导轴承处的位移频谱图。在0.6Q工况时，振动频率成分较为复杂，其他工况下振动频率成分包括半频、轴频和叶频，其中半频幅值最大，而轴频和叶频表现不明显，表明不同工况下轴承处的振动以轴承自身的半频振动为主。

图5 轴承-转子系统在导轴承处的位移频谱Fig.5 Displacement spectrum diagram of bearing-rotor system at the guide bearing

图6示出不同工况下的叶轮位移响应，图7示出不同工况下，转子系统在叶轮处的位移频谱。受径向力影响，叶轮振动位移规律与径向力规律相近，在每个旋转周期内存在5个次高峰。叶轮振动位移在不同工况下表现出明显的差别，振动峰对峰值在0.6Q下最大，达到1.483 mm，位移最大值为0.794 mm。设计工况下，叶轮振动峰对峰值为0.343 mm，位移最大值为0.185 mm。从叶轮振动的频谱可以看出，叶频幅值最大，半频、轴频幅值较小，根据振动位移和频谱分析，叶轮振动主要受叶轮处激励力影响，叶轮振动规律与径向力的分布规律相关，呈现出周期性的5个峰值数。与导轴承处的振动位移相比，叶轮振动位移更大。导轴承主要承受径向力，转子在导轴承处的振动位移最小，远离导轴承，振动位移增加。设计工况下，径向振动位移最小、幅值最小，偏离设计工况越大，径向振动位移越大、幅值越大。

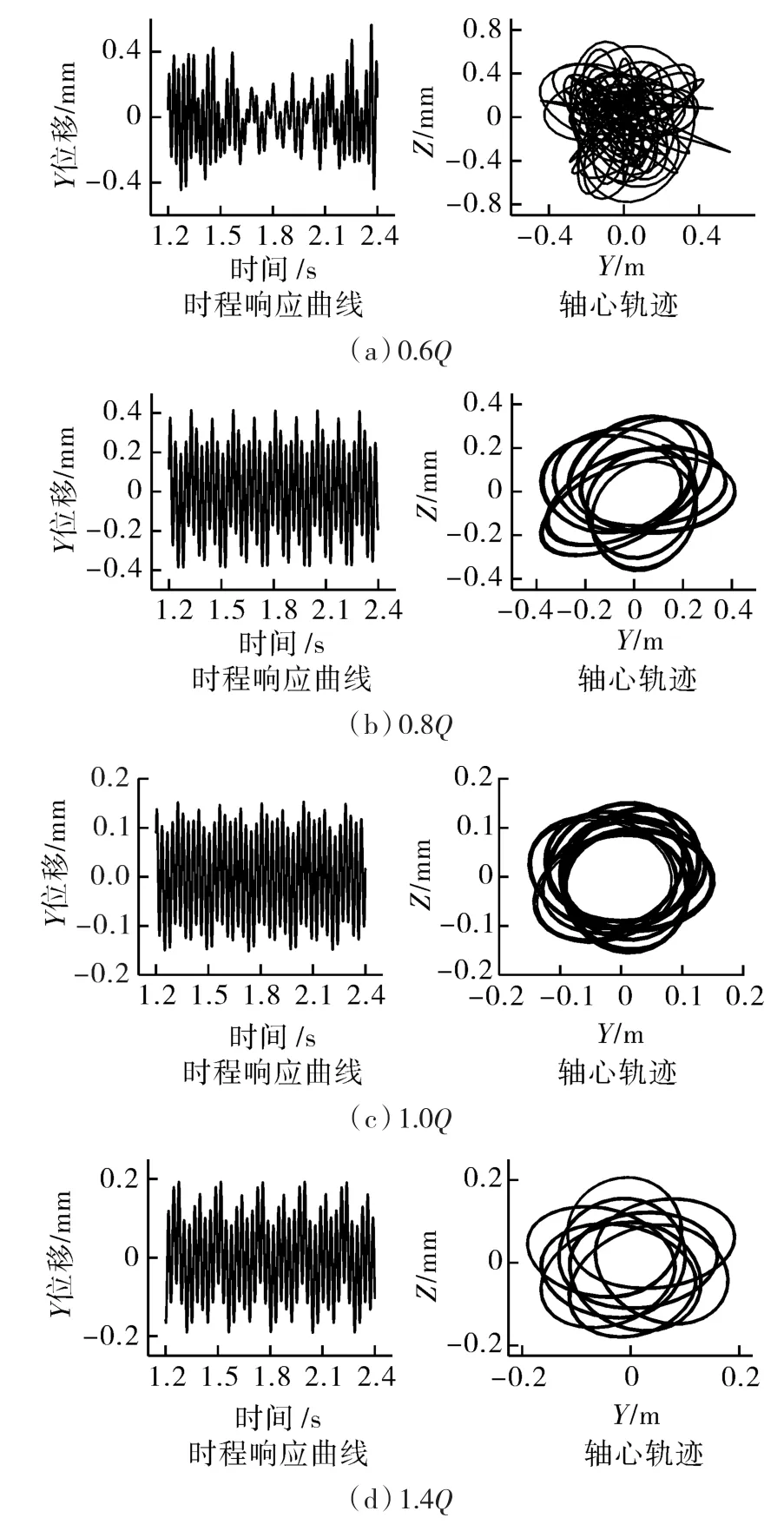
图6 轴承-转子系统在叶轮处的位移响应Fig.6 Displacement response of bearing-rotor system at the impeller

图7 轴承-转子系统在叶轮处的位移频谱Fig.7 Displacement spectrum diagram of bearing-rotor system at the impeller

针对立式蜗壳泵转子系统在0.6Q工况下的运行不稳定，通过对比0.6Q和设计工况下轴承的油膜分布，探讨转子系统在0.6Q工况下运行不稳定的机理。瞬态油膜压力分布存在正压区和负压区，其中正压区主要承受外部载荷。图8示出设计工况下导轴承的油膜压力分布，由图可以看出，从2.368～2.386 s，油膜压力承载区的中心近乎处于轴承中心，呈现规律性的椭圆形状，承载面积大，压力梯度大，随着转子的转动，油膜始终处于稳定的双油楔分布状态，高、低压区域沿周向逆时针移动，转子系统运行稳定。

图8 设计工况下导轴承油膜压力分布Fig.8 Pressure distribution of the oil film in guide bearing under design condition

图9示出0.6Q工况下油膜的压力分布。由图可以看出，从2.368～2.38 s，叶片旋转36°，即转子转动1/10个周期，油膜呈双油楔和四油楔分布。随着转子的转动和径向力的变化，高压区沿圆周方向逆时针移动。在移动的过程中，由于径向力过大，导致油膜状态不稳定。从3.368～3.371 s，高压区的压力中心位置沿轴向下移，低压区的压力中心位置沿轴向上移，并在高压区的轴向上方出现次低压区，低压区的轴向下方出现次高压区。高压区最高压力值减小，压力承载区面积减小，压力梯度减小，轴承承载力减小，油膜状态发生变化，出现扁长的四油楔分布。从2.371～2.374 s，次低压区的中心位置沿轴向下移；次高压区的中心位置沿轴向上移，最高压力值增大，压力承载区面积增大；高压区的中心位置沿轴向下移，最高压力值减小，压力承载区面积减小，逐渐形成高压区与次高压区最高压力值、压力承载区面积相近的四油楔分布。从2.374～2.377 s，次高压区的中心位置沿轴向上移，最高压力值增大，压力承载区面积增大，压力梯度增大，轴承承载力增加，形成新的高压区域，成为主要压力承载区域，油膜由四油楔分布逐渐转变为双油楔分布。从2.377～2.38 s，高压区的中心位置继续沿轴向上移，最高压力值增大，压力承载区面积增大，压力梯度增大，轴承承载力增大。压力承载区呈现椭圆形状并近乎处于轴承的中心，油膜趋于稳定。

图9 0.6Q工况下导轴承油膜压力分布Fig.9 Pressure distribution of the oil film in guide bearing under 0.6Q condition

与设计工况下对应时刻的油膜相比，小流量工况下，轴承油膜处于双油楔和四油楔的交替变化中，导致了油膜分布不稳定。四油楔状态下，油膜压力承载区的中心严重偏离轴承中心，出现两个对称的高压中心和低压中心，压力承载区呈扁长形状，承载面积小，抗干扰能力差，导致转子系统运行不稳定。

3 结论

（1）叶轮与蜗壳的动静干涉作用对径向力影响较大，采用双蜗壳结构后，径向力明显减小，转子在轴承处的振动峰对峰值和总位移最大值均显著减小。叶轮的振动峰对峰值与总位移最大值在非设计工况下均有显著降低。

（2）不同工况下，转子的振动位移分量都表现出明显的周期性，转子在导轴承处的振动周期是转子旋转周期的2倍。叶轮振动周期与转子旋转周期一致；随着偏离设计工况点，转子的振动峰对峰值和位移最大值均有所增加。

（3）小流量工况下，导轴承油膜处于双油楔和四油楔交替变化中，四油楔油膜的出现是转子系统运行不稳定的主要原因。