基于对称不确定性和三路交互信息的特征子集选择算法

顾翔元，郭继昌，李重仪，肖利军

(天津大学电气自动化与信息工程学院，天津 300072)

计算机技术的快速发展，使得各种数据量快速增长，智能信息处理所需数据集的特征维数也越来越高.数据集特征维数的增加，会带来分类准确率下降、计算耗时多等问题．因此有必要进行特征选择[1-4].

特征子集选择是特征选择的一种重要方法[5]，它利用某种度量标准对特征与类标签的相关性以及特征间的冗余性进行度量，消除不相关特征和冗余特征．度量标准是影响特征子集选择算法效果好坏的关键．

文献[6-7]利用互信息实现了特征选择，互信息是一种常用的度量标准，它具有可描述特征间的非线性相关性和空间变换不变性等优点[8]，但其优先选取的特征不能保证取得较好的分类效果．文献[9]对互信息进行了归一化处理，提出了对称不确定性(symmetric uncertainty，SU)度量标准．FCBF[10]和FCBF-MIC 算法[11]利用对称不确定性进行了特征子集选择．FCBF 算法采用对称不确定性度量特征与类标签的相关性以及特征间的冗余性，并将特征与类标签的对称不确定性和特征间对称不确定性做比较来消除冗余特征．FCBF-MIC 算法分别采用对称不确定性和最大信息系数对特征与类标签的相关性以及特征间的冗余性进行度量，并利用特征与类标签的最大信息系数和特征间的最大信息系数的比较结果来消除冗余特征．由于仅利用对称不确定性或最大信息系数等某一种度量标准来评价冗余特征，FCBF 和FCBF-MIC 等算法存在将相关特征当作冗余特征而消除的问题．

针对上述问题，本文提出一种基于对称不确定性和三路交互信息的特征子集选择算法，首先利用对称不确定性进行相关性分析，消除不相关特征，然后分别利用对称不确定性和三路交互信息进行冗余性分析和交互性分析，消除冗余特征．本算法由于利用了对称不确定性和三路交互信息两种度量标准而减少了相关特征的误消除，使得有效特征得以保留，因此算法获得了更好的性能．

1 三路交互信息和马尔可夫毯

1.1 三路交互信息

信息熵被用来量化某随机变量信息量的大小，其定义如式(1)所示．

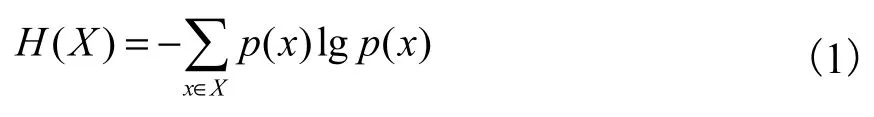
式中p(x)为一离散随机变量X取值为x的概率．

互信息被用来表述两变量所包含信息量的多少，两变量X和Y的互信息I(X；Y)定义如式(2)所示．

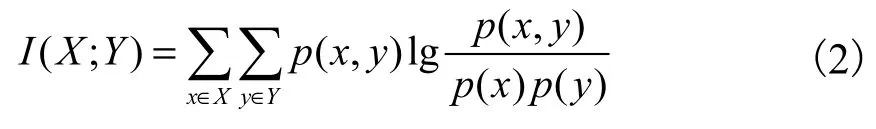
式中：p(x，y)为两变量的联合概率密度函数；p(y)为变量Y取值为y的概率．I(X；Y)值越大，表明X和Y所包含的共同信息越多．

三路交互信息I(X；Y；Z)是互信息的扩展，其可为正、负和零．当I(X；Y；Z)为正值时，表明两变量X和Y共同提供关于Z的信息要大于它们单独提供关于Z信息的和，此时表明X和Y在提供关于Z的信息上是互补的；其值为负值时，表明X和Y在提供关于Z的信息上是冗余的；其值为零值时，表明两变量在提供关于Z的信息上是独立的．

1.2 马尔可夫毯

马尔可夫毯可被用于特征选择中，其定义[10]如下．

定义1(马尔可夫毯) 给定一个特征fj，类标签c，一个特征集F和F中一个特征子集Gj．假设Gj⊂F(fj∉Gj)，Gj为fj的马尔可夫毯的条件是概率p(F－Gj－{fj}，c|fj，Gj)＝p(F－G－{fj}，c|Gj) ．

由定义1 可知，如果选取fj，前后概率不变，则Gj为fj的马尔可夫毯．基于马尔可夫毯，对冗余特征有这样的定义：假设F是当前特征集，F中的一个特征fj是冗余特征当且仅当存在Gj⊂F(fj∉Gj)为fj的马尔可夫毯[10]．

马尔可夫毯可以被用来评价冗余特征，然而由于运算量较大，其很少被使用，通常利用不同形式的近似马尔可夫毯．如定义2 所示，文献[10]给出一种近似马尔可夫毯来评价冗余特征．

定义 2(近似马尔可夫毯) 特征fs是特征fi的近似马尔可夫毯当且仅当同时满足SU(c，fs)≥SU(c，fi)和SU(fi，fs)≥SU(c，fi) ．

由定义2 的SU(fi，fs)≥SU(c，fi)可知，文献[10]将特征与类标签的对称不确定性和特征间的对称不确定性做比较，利用比较结果来评价冗余特征．由于只考虑两个特征来评价冗余特征，使得满足SU(fi，fs)≥SU(c，fi)条件的特征未必是冗余特征，会将一些相关特征当作冗余特征而消除．

2 本文算法

本文算法主要分为两个步骤：首先消除不相关特征，然后消除冗余特征，具体过程如图1 所示．

图1 中，首先计算特征与类标签的对称不确定性值，消除其值为零的特征；然后，计算特征间的对称不确定性值，按其和特征与类标签的对称不确定性值的大小确定它们的序值，并计算特征与类标签的三路交互信息值．若某特征满足以下条件：其与其他特征的对称不确定性值和序值分别大于其与类标签的对称不确定性值和序值，其与其他特征、类标签的三路交互信息值小于零，则将其作为冗余特征消除．

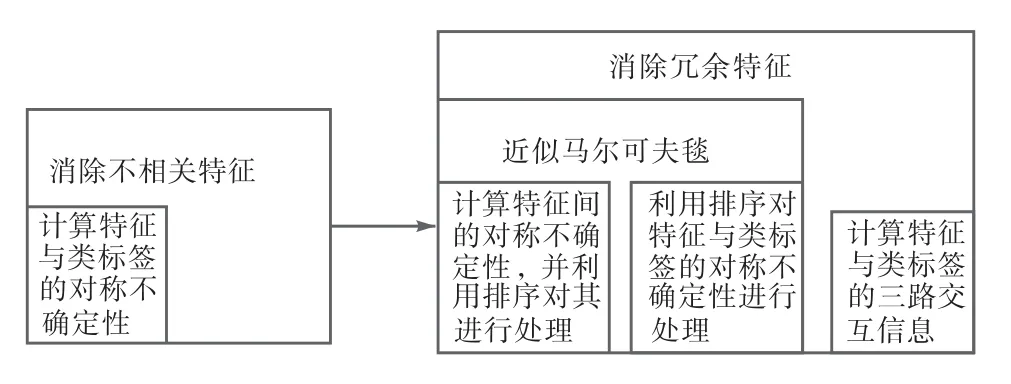
图1 本文算法的框架Fig.1 Framework of the proposed algorithm

2.1 相关特征的评价

相关性通常是指单个特征与类标签的关系．利用对称不确定性进行相关性分析，特征fi与类标签c的对称不确定性SU(c，fi)如式(3)所示．

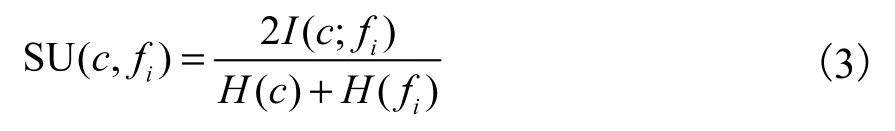
式中SU(c，fi) ∈[0 ，1] ．与类标签的对称不确定性值越大，表明该特征与类标签越相关；当与类标签的对称不确定性值为零时，表明该特征与类标签是不相关的．定义3 给出相关特征的评价方法．

定义 3(相关特征的评价方法)fi是相关特征当且仅当满足SU(c，fi)＞0．

2.2 冗余特征的评价

利用定义3 将不相关特征从原始特征集中消除后，需要消除冗余特征．接下来进行冗余性分析．

冗余性通常是指特征间的关系．利用对称不确定性进行冗余性分析．

鉴于文献[10]中近似马尔可夫毯存在的问题，分别利用排序对SU(c，fi)和SU(fi，fs)进行处理，得到其序值R(c，fi)和R(fi，fs) ．由于对称不确定性的最大值为1，最小值为0，而不同序值间最小的差别为1．所以，对于不同的fi，R(c，fi)间的差别要大于SU(c，fi)间的差别；对于同一个fi和不同的fs，R(fi，fs)间的差别要大于SU(fi，fs)间的差别．使得R(c，fi)和R(fi，fs)的部分比较结果较SU(c，fi)和SU(fi，fs)的比较结果有一定的优势．

如果只利用R(c，fi)和R(fi，fs)的比较结果来定义近似马尔可夫毯，由于量级不对等，会存在一些比较结果不准确的问题．

而将SU(c，fi)和SU(fi，fs)的比较结果与R(c，fi)和R(fi，fs)的比较结果相结合来定义近似马尔可夫毯，不但可以减少将相关特征当作冗余特征而消除的情况，而且结果也更为准确．所以，如定义4 所示，给出一种近似马尔可夫毯．

定义 4(近似马尔可夫毯)fs是fi的近似马尔可夫毯当且仅当同时满足 SU(c，fs)＞SU(c，fi)、SU(fi，fs)＞SU(c，fi)和R(fi，fs)＞R(c，fi)．其中，R(c，fi)和R(fi，fs)分别是SU(c，fi)和SU(fi，fs)经排序而得到的序值．

由定义4 可知，同时满足SU(fi，fs)＞SU(c，fi)和R(fi，fs)＞R(c，fi)条件的特征才是冗余特征，可以保证效果较显著的特征被保留．由于只考虑一种度量标准，会存在将相关特征当作冗余特征而消除的问题．鉴于此，接着进行交互性分析．

交互性通常是指两个或多个特征与类标签的关系．利用三路交互信息进行交互性分析．

由第1.1 节可知，当I(fi；fs；c)＜0 时，特征fi与fs 共同提供关于类标签c的信息要小于它们单独提供关于c信息的和，可以表明fi与fs在提供关于c的信息上是冗余的．因此，在定义4 的基础上，引入三路交互信息，给出冗余特征的评价方法．

定义 5(冗余特征的评价方法) 候选特征fi是冗余特征当且仅当同时满足 SU(fi，fs)＞SU(c，fi)、R(fi，fs)＞R(c，fi)和I(fi；fs；c)＜0．

在近似马尔可夫毯的基础上，引入三路交互信息来评价冗余特征，可以进一步减少将效果显著的相关特征当作冗余特征而消除的情况．

2.3 算法实现

利用定义3 和定义5，本文实现一种基于对称不确定性和三路交互信息的特征子集选择算法(简记为SUTII)，该算法的伪代码如下．

SUTII 算法分为两部分：第1 部分(第1～8 行)，先对候选特征集X、已选特征集S和与c相关的特征集Y进行初始化，然后计算X中的特征与c的SU，将与c相关的特征放入Y中，并将这些特征做降序排序；第2 部分(第9～32 行)，先从Y中取出一个SU为最大值的特征，并放入S中；然后计算fi与S中特征的SU 和c、fi与S中特征的三路交互信息，并分别对SU(c，fi)和SU(fi，fs)进行排序处理，得到R(c，fi)和R(fi，fs)；接着将SU(fi，fs)与SU(c，fi)、R(fi，fs)与R(c，fi)以及I(fi；fs；c)与零值做比较，如果SU(fi，fs)大于SU(c，fi)、R(fi，fs)大于R(c，fi)和I(fi；fs；c)小于零，将fi从Y中消除．按照上述步骤选取特征，直到Y中的特征少于2 个结束．最后，如果Y中有一个特征，将该特征放入S中．

3 实验结果

3.1 数据集和实验设置

表1 给出用到的数据集，它们均取自UCI 机器学习数据库[12]和ASU 特征选择数据库[13]．采用J48、IB1 和Naïve Bayes 分类器，其参数取WEKA[14]默认参数．采用最小描述长度离散方法[15]．特征选择过程用到ASU 特征选择软件包[16]．实验中，SUTII算法的参数δ取10-10．

为减小随机性对最终结果的影响，进行10 次十折交叉验证方法[17]处理，将10 次结果的平均值作为最终结果，十折交叉验证是将数据集分成10 等份，其中9 份作为训练集，剩余的1 份作为测试集，依次进行，直至所有的数据集都为测试集；此外，利用显著性水平为5%的单边配对样本t检验进行显著性检验．

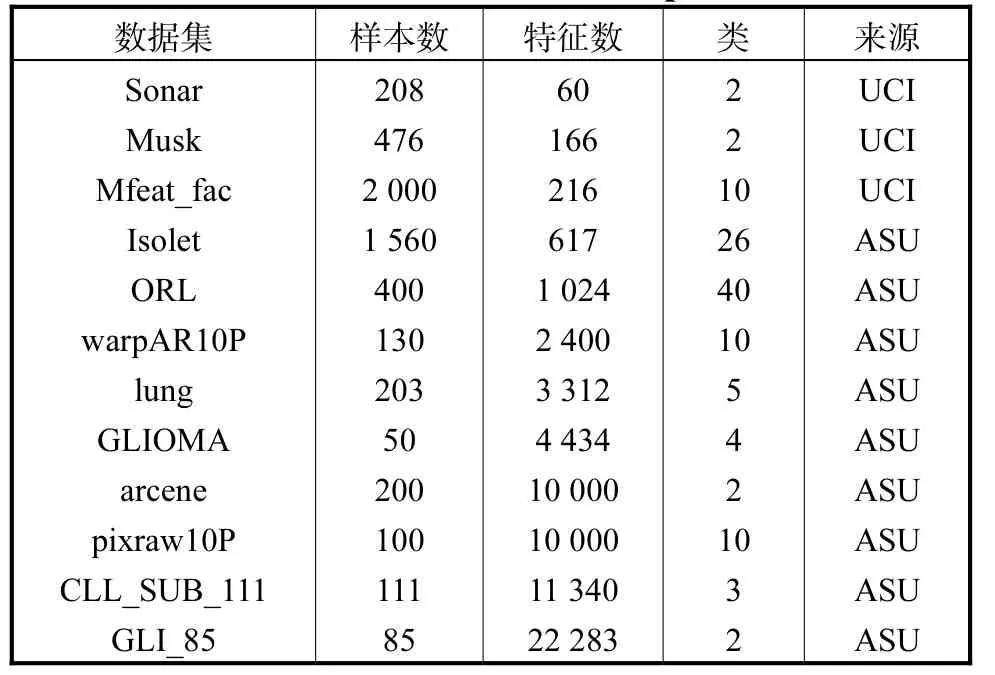
表1 实验中用到的数据集Tab.1 Used datasets in the experiment

为验证SUTII 算法的特征选择效果，将其与FCBF-MIC[11]、SAOLA[6-7]、FCBF[10]和 NFCBF 算法[18]做比较．表2～表4 分别给出这些算法利用J48、IB1 和Naïve Bayes 分类器选取特征的分类准确率，W/T/L 行给出利用单边配对t检验而得到的值，其中，W、T 和L 分别表示SUTII 算法显著优于、无显著和显著劣于其他算法的数据集数．表5 给出这些算法选取的特征数，表6 给出这些算法特征选择的用时．

3.2 实验结果与分析

由表 2 可知，SUTII 算法的平均值最大，而FCBF-MIC 算法的平均值最小．由W/T/L 值可以得到，SUTII 算法优于NFCBF、FCBF-MIC、SAOLA 和FCBF 算法的数据集数分别为4、10、2 和2 个，而劣于这些算法的数据集数分别为2、0、0 和0 个，从而得知SUTII 算法的特征选择效果优于另外4 种算法.

表3 表明，SUTII 算法的平均值最大．由W/T/L值可知，SUTII 算法优于 NFCBF、FCBF-MIC、SAOLA 和FCBF 算法的数据集数分别为6、8、8 和3个，与表2 相比，SUTII 算法较SAOLA 和FCBF 算法的优势有所增加．

表4 中，NFCBF 算法的平均值较大．W/T/L 值表明SUTII 算法的特征选择效果略优于FCBF 算法、显著优于FCBF-MIC 和SAOLA 算法，而和NFCBF 算法相当．

由表5 的平均值可知，SAOLA 算法选取的特征最少，SUTII 算法选取的特征与FCBF 算法相当，而多于FCBF-MIC 和SAOLA 算法，NFCBF 算法选取的特征最多，明显多于其他4 种算法．SUTII 算法在如Sonar 和 Mfeat_fac 等数据集上选取的特征占数据集全部特征的比重较大，而在如 arcene、CLL_SUB_111 和GLI_85 等数据集上选取的特征占的比重较小．

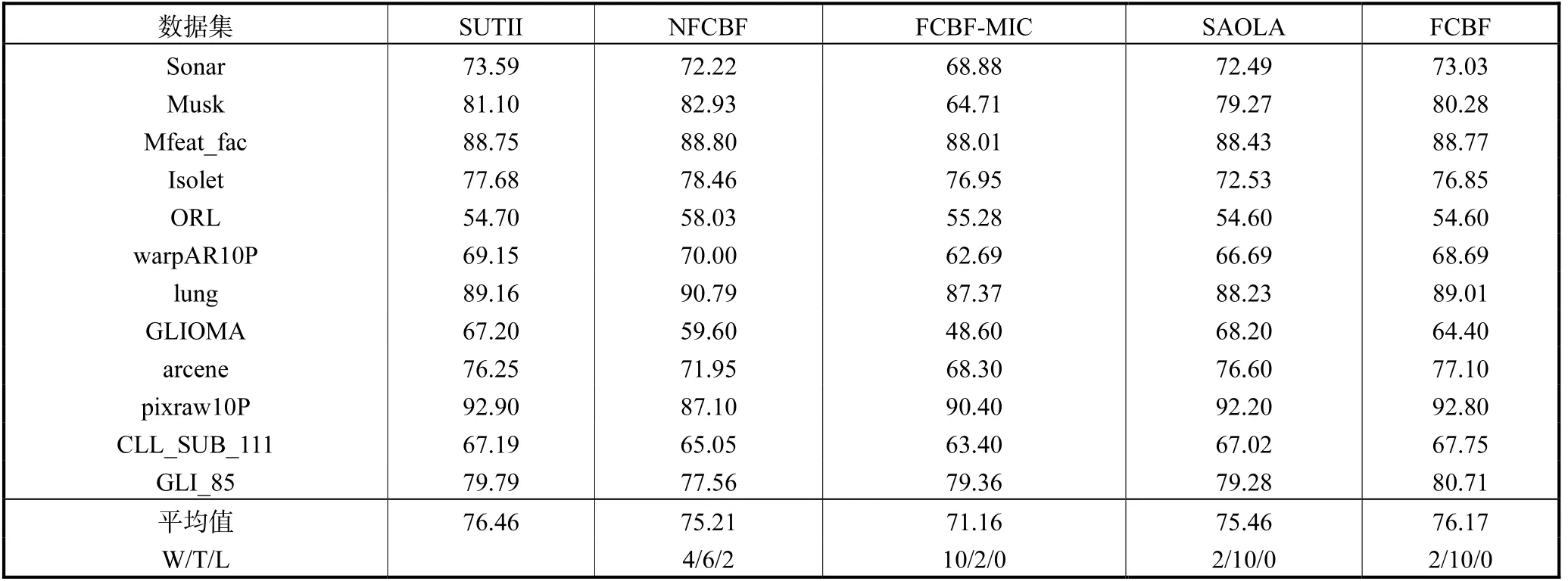
表2 利用J48分类器选择特征的平均分类准确率Tab.2 Average accuracy with J48 classifier on the selected features %

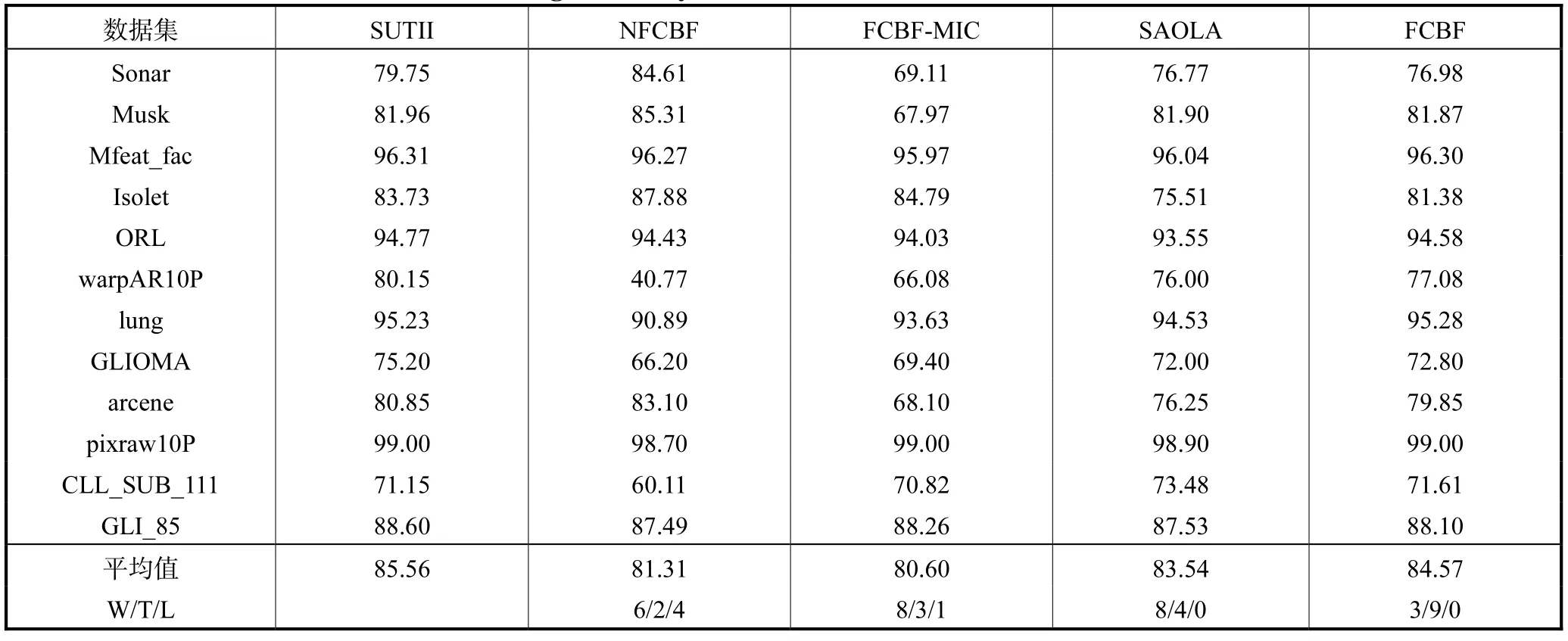
表3 利用IB1分类器选择特征的平均分类准确率Tab.3 Average accuracy with IB1 classifier on the selected features %

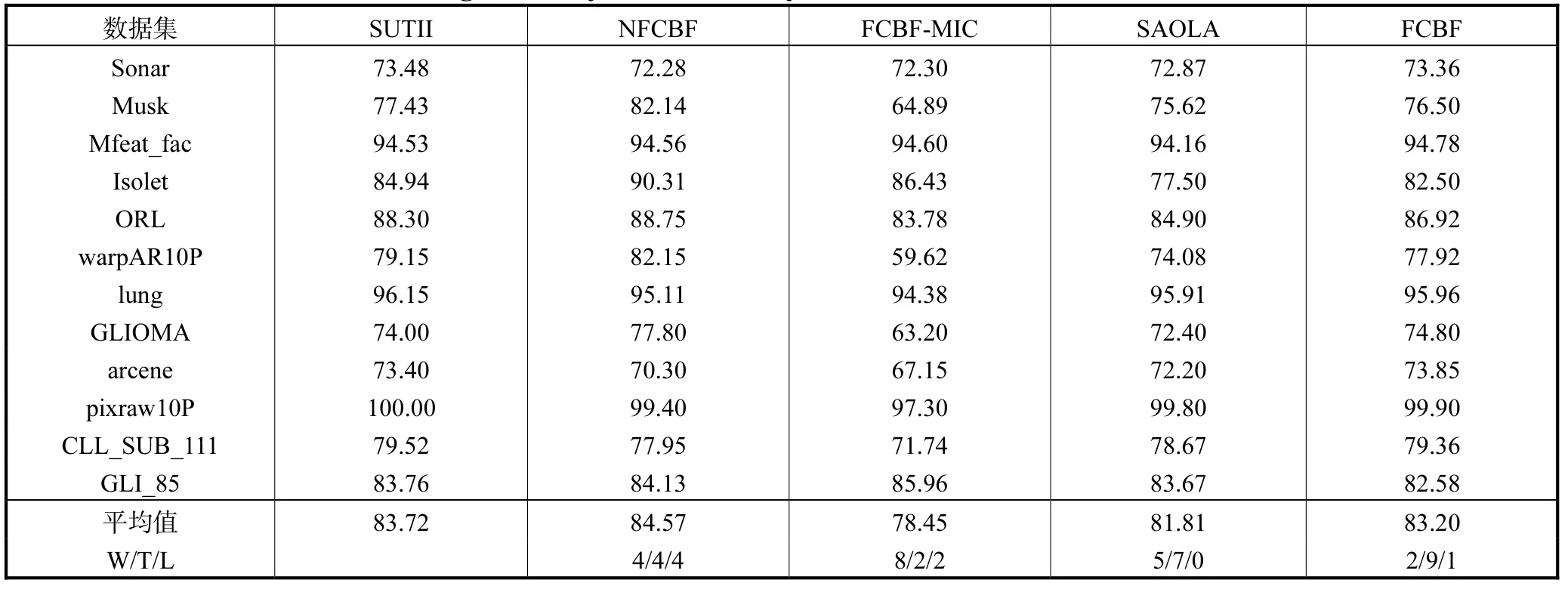
表4 利用Naïve Bayes分类器选择特征的平均分类准确率Tab.4 Average accuracy with Naïve Bayes classifier on the selected features %

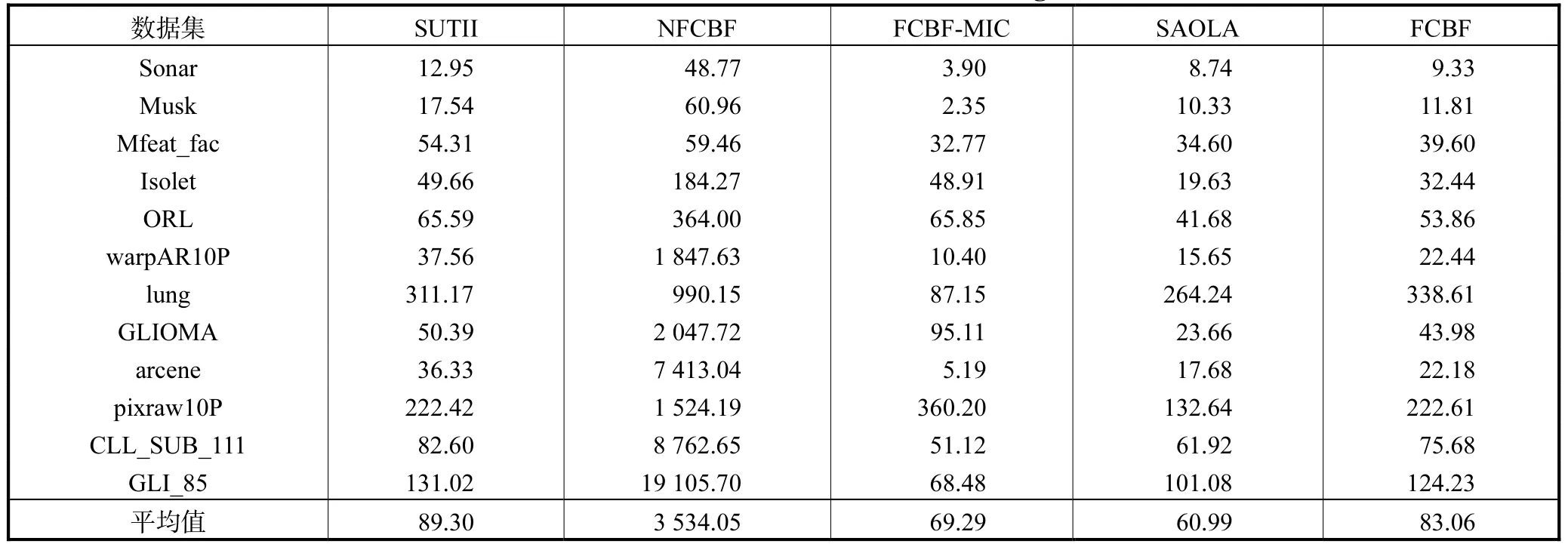
表5 各算法选择的特征数Tab.5 Number of selected features of different algorithms

表6 中，平均值表明SUTII、SAOLA 和FCBF 算法的特征选择用时较少，明显少于NFCBF 和FCBFMIC 算法；NFCBF 算法在如arcene、CLL_SUB_111和GLI_85 等数据集上的用时较多，而FCBF-MIC 算法在如Mfeat_fac、Isolet 和ORL 等数据集上的用时较多．

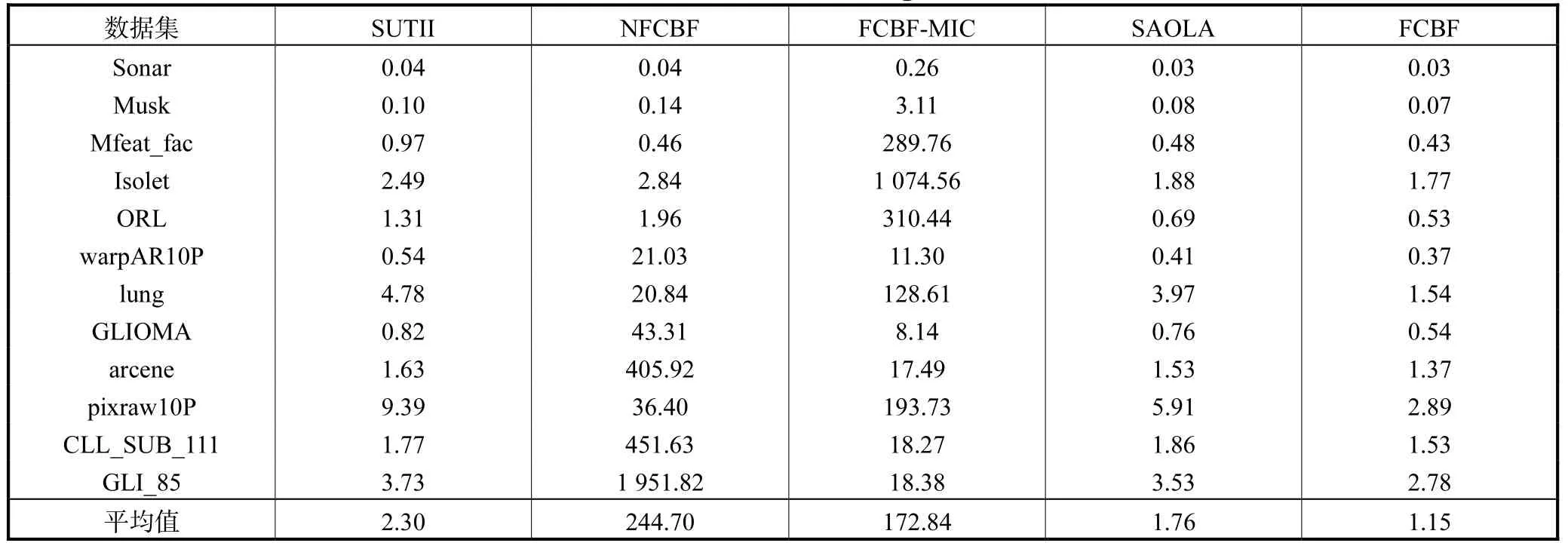
表6 各算法的用时Tab.6 Time of different algorithms s

4 结 语

本文采用对称不确定性进行相关性分析和冗余性分析，利用三路交互信息进行交互性分析，提出一种基于对称不确定性和三路交互信息的特征子集选择算法SUTII．为验证SUTII 算法的性能，利用J48、IB1 和Naïve Bayes 分类器将其与另外4 种特征子集选择算法NFCBF、FCBF-MIC、SAOLA 和FCBF 在3个UCI 数据集和9 个ASU 数据集上做对比实验．实验结果表明，SUTII 算法能够取得较好的特征选择效果，同时选取的特征较FCBF-MIC、SAOLA 和FCBF算法有所增加，验证了所提冗余特征的评价方法能够减少将相关特征当作冗余特征而消除的情况，使一些效果较显著的特征得以保留．