基于Logistic 回归深层神经网络的电力系统故障概率诊断

2021-12-26林济铿任怡睿翟明玉

天津大学学报(自然科学与工程技术版) 2021年2期

林济铿，任怡睿，闪鑫，李俊，翟明玉，王波

(1. 同济大学电子与信息工程学院，上海201804；2. 南瑞集团(国网电力科学研究院)有限公司，南京211106；3. 国电南瑞科技股份有限公司，南京211106；4. 智能电网保护和运行控制国家重点实验室，南京 211106)

当电力设备发生故障时，调度中心会同时收到大量的信号，如何从大量信号中快速辨识出发生故障的设备，即所谓的“故障诊断”，对于保证和提升系统运行安全性具有重要意义，并成为电力调度中心的标配软件．

迄今为止，电力系统故障诊断的主要方法包括专家系统、解析模型、Petri 网、人工神经网络等．

专家系统通过构建专家知识库及推理机制实现根据专家经验获得设备故障与否的判断．该类方法因原理相对简单、运行稳定而成为实际电力系统故障诊断中应用最广泛的方法[1]．周明等[2]、赵伟等[3]分别将专家系统与模糊系统和多智能体技术相结合应用于故障诊断问题．史家燕等[4]采用多种数据源对变压器各种可能发生的故障进行综合诊断．如何有效地获取专家经验知识，如何使得推理机制具有扩展性，是该类方法尚需克服的问题．

解析模型方法构建可疑故障区域内的各种候选故障设备及相应的信息状态的理想与实际间差异最小化优化模型，通过优化的方法求得其最有可能的故障元件．Wen 等[5]和He 等[6]分别采用tabu 算法和粒子群算法对解析模型进行了求解．董明等[7]和刘道兵等[8]进一步利用了PMU 量测单元信息与不确定时间发生概率等先验知识．该类方法具有较好的理论支撑，但其往往会得到多解，尚有待进一步克服和提升.

Petri 网以图形的方式表示被保护元件、开关、保护等所组成系统的逻辑关系，从设备的相互逻辑关系角度分析设备故障发生过程．孙静等[9]将Petri 网与模糊信息相结合．贾学涵等[10]基于Petri 网考虑保护和断路器可能发生的拒动误动情况建立多因素分级模型．白展等[11]通过计及时间约束增强模型的容错性．该类方法需要较充分的设备故障的先验概率数据，而这些数据往往又较难获得，相应地限制了其应用．

神经网络方法把开关及故障信息作为网络的输入，而相应设备的故障与否信息作为网络的输出，具有在线运行简单快速及强容错的特点[12]．2000 年左右及之前的神经网络故障诊断方法受限于计算机的计算能力及神经网络理论的发展，通常采用浅层神经网络模型，当输入层的维数不高(往往采用单隐层)、样本数量不大的情况下，取得不错的效果．Bi 等[13]、孙雅明等[14]、廖志伟等[15]分别建立了基于数据挖掘的浅层神经网络、径向基神经网络、广义回归神经网络的诊断模型．此时的神经网络方法因训练样本量往往较少，而使得其外推的能力有所欠缺，且训练的时间较长．

随着近年来计算机硬件和深度学习理论与算法的飞速发展，基于深度神经网络的故障诊断方法成为了最有希望改善故障诊断现有问题并把故障诊断水平提升到一个新高度的方法．王丽华等[16]、赵洪山等[17]将深度自编码网络应用于电机故障诊断．黄良等[18]以过去近10 年某一具体电网的故障数据作为训练集，实现对于所构建循环神经网络模型的训练和学习．实际上，样本数量上的不足与质量上的参差不齐是深度学习神经网络类方法应用于工程问题普遍存在的一大阻碍，有学者采用无监督预训练的方式对这一问题进行改善[19-20]，但现有方法仍未从根本上解决问题．

根据笔者对多个电力公司调度中心的调研，上述各类方法在实际工程中应用较多的是基于专家系统的故障诊断方法，具有很高的实际故障辨识率和很低的漏报率．目前困扰电力公司的主要问题是该方法的误报率偏高．

基于以上综述及当前电力公司故障诊断系统面临的问题，本文提出了基于Logistic 回归和深度学习的故障诊断新模型及算法，以实现故障诊断准确率的提升．该模型对于每一元件建立相应的回归型深度学习神经网络，输入为包含事故总信号、开关和保护信号在内的SCADA 数据，输出为相应元件的故障概率，并基于RMSprop 方法对于神经网络进行训练和学习；进而，针对深度学习所需样本数较大而实际电力系统故障历史记录较少这一现实困难问题，本文进一步提出了一种记录扩充提取及样本模拟生成方法以实现模型的顺利训练．通过算例证明了本文所建立故障诊断模型及样本扩充方法的正确性与可行性．

1 深度学习Logistic 回归神经网络故障诊断模型的构建

目前深度学习神经网络模型非常多，但其大多基于卷积神经网络、循环神经网络与全连接神经网络等根据特定问题的需要进行相应的变化而得到，其中卷积神经网络关注输入特征向量或特征矩阵中的相邻特征间的关系，因此适用于图像处理领域；循环神经网络的输出由当前输入与之前时刻的输出共同决定，因此适用于时序相关问题如本文和语音处理等领域；全连接神经网络是一种经典前馈神经网络，且被证明能以任意精度拟合任意复杂度的函数[21]．而Logistic回归模型是研究观察结果与其影响因素之间关系的一种多变量分析方法，近年来在医学、金融等类似二分类问题上得到了广泛应用[22]，具有较强的回归能力．因此本文选择构造基于回归模型的深度学习神经网络全连接神经网络来实现电力系统的故障诊断，以提升其故障诊断的正确率．

1.1 Logistic回归模型

电力系统设备的故障诊断问题为二分类问题，用y 表示样本观测值，则正类 y =1表示设备故障，负类y= 0表示设备无故障．Logistic 回归为概率型非线性回归模型，若用x 表示相应设备的输入样本特征，设备故障概率 hθ( x )用Logistic 回归模型可表示为

式中：θ 为模型参数；g (θ, x)为分类边界，其具体计算式由待拟合的函数形式决定．则设备无故障的概率为

假定有N 个样本，其观测值分别为1y ，y2，…，iy ，…， yN，对应样本特征为向量X1， X2，…，Xi，…，XN，综合式(1)、式(2)可以得到观测值 yi的概率为

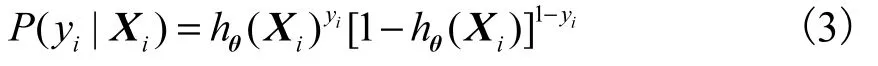
若样本之间互相独立，用极大似然估计调整模型参数θ，则由式(3)可以得到似然函数为

采用优化方法即可求得参数θ 使得对数似然函数ln L ( θ) 取得最大值．

1.2 用于故障诊断的全连接Logistic 回归深度神经网络构建及训练学习方法

1.2.1 用于故障诊断的全连接Logistic 回归深度神经网络构建

本文选择构造全连接神经网络来实现式(5)对于参数θ 的优化，即构建基于回归模型的深度学习神经网络，实现对于电力系统设备包括遥信信号等的信息向量与元件故障概率间的函数关系的准确拟合．其中，神经网络的输入即回归模型的输入x，输出即回归模型的输出 hθ( x )，连接神经元之间的权重与偏置即为回归模型的待调整参数θ，式(5)中的对数似然函数ln L ( θ )的相反数为网络损失函数E；以最小化损失函数为目标通过对神经网络的训练学习，即对于参数θ 的优化调整，相应实现对Logistic 回归模型的建立．进而即可依此训练好的网络对相应的元件进行故障的概率诊断．

图1 所示为任一神经元结构[23]，其中x 为输入，w 为权重，b 为偏置，f 为激活函数为激活函数的输入，a=f ( z)为激活函数应变量，即神经元输出值．

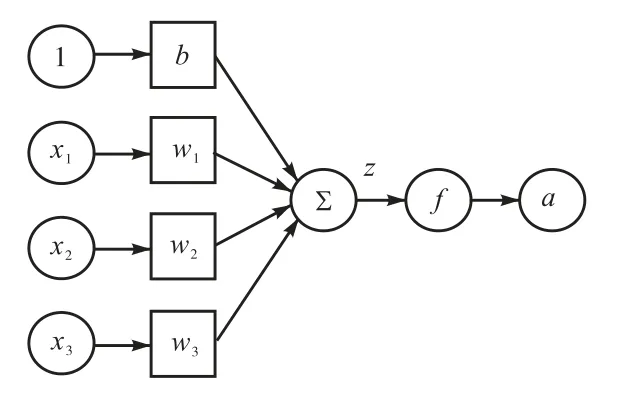
图1 神经元结构Fig.1 Structure of a neuron

由如图1 所示的神经元经链接而构成的含三隐层的全连接Logistic 回归神经网络的整体结构如图2所示．

图2 中，l0为输入层，该层神经元个数 n0等于所构建的样本特征向量位数；l1～l3为隐含层，l4为输出层，li( i=1,2,3,4)层的每个神经元xi,j( j∈[1, ni])均与li-1中的每一神经元xi－1,k( k∈[1, ni－1])相连，其连接权值为wi,k,j．隐含层 l1～ l3神经元的激活函数为Relu函数，如式(6)所示；输出层神经元 x4,1的激活函数为Logistic 函数如式(1)所示的 hθ( x )，其输出a 即为网络输出，表示样本对应的事件概率．而 x4,1的输入即x3,1,… ,x3,n3的加权和，亦即式(1)中的 g ( θ , x )．

网络最小化目标-损失函数E 的计算式为

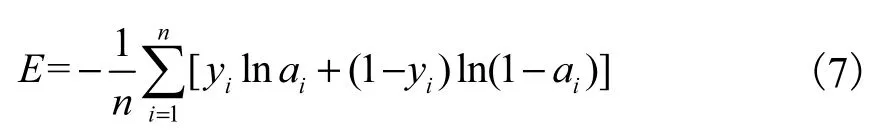
式中：n 为样本数量；ai和 yi分别表示第i 个样本对应的网络输出和样本标签．

1.2.2 训练学习方法

神经网络训练过程即网络中的所有权重与偏置的更新优化过程，本文的参数优化方法为RMSprop方法[24]．若目标E 关于所有参数θ (wi,k,j，bi,j，i=1,2,3,4，k∈[1, ni－1]， j∈[1, ni])的参数梯度用表示，对于第t 次参数修正，其更新过程如下．

步骤1根据微分的链式法则，计算当前的所有参数梯度

步骤2计算当前参数梯度与上一次参数梯度的平方加权和 ΔS ．

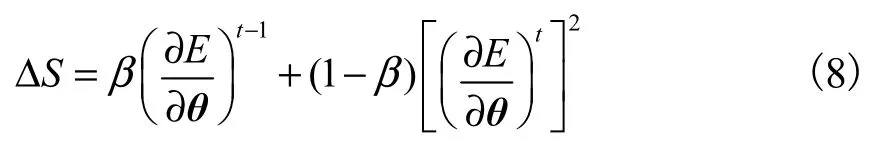
式中β为可调参数，本文取0.9．

步骤3更新参数．

式中：α为可调参数，本文取0.001；ε为平滑项，用于避免分母为0，本文设为10－6．

2 深度学习Logistic 回归神经网络的故障诊断样本结构及样本扩充方法

对于第1 节所构建的深度学习神经网络需要大量样本来训练，而实际上因设备的可靠性高，以及电网中的设备隐患排查制度执行比较彻底，使得设备故障发生的次数很少，相应历史记录也较少而使得能用于训练的样本不足．故本文进一步提出了一种基于电力系统近似故障记录提取及模拟样本生成的样本扩充方法，从而能够产生足够样本，以实现对第1 节所构建的故障诊断深度学习神经网络的成功训练．

2.1 样本结构

每一训练样本由样本标签和样本特征向量两部分组成．样本标签为0-1 变量，表征设备真实故障情况(1 表示故障，0 表示无故障)．若诊断对象为某一线路，配备一套主保护且其首末端分别连接一个断路器，则该线路故障诊断的模型输入特征向量如表1 所示．若诊断对象为发电机变压机组中的变压器，只有一端连接断路器，则该变压器的故障诊断模型输入特征向量如表2 所示．其他元件故障诊断模型的输入特征向量构造方法与此类似．

表1 线路故障特征向量Tab.1 Feature vectors of faults on a transmission line

表2 变压器故障特征向量Tab.2 Feature vectors of faults on a transformer

对于表1 和表2 中的属性，值为1 表明调控中心收到相应信号，-1 表示未收到信号．线路功率和变压器功率等模拟信息来自SCADA 遥测数据，选择收到第1 个相关的遥信信号时刻前4 个与后6 个SCADA功率采样数据，若这10 个功率采样数据中存在任意相邻两个数据差超过额定值的50%，则“功率变化”属性值为1，否则为-1；第1 个遥测数据为0 则“最初功率为0”属性值为1，否则为-1；最后一个遥测数据为0 则“最终功率为0”属性值为1，否则为-1．

构建样本时，保护和开关动作信号需要进行初步检测以判定动作信号是否有效．当出现任意以下情况之一时，认为相应动作信号无效，当作未收到信号处理，属性值为-1：

(1) 开关或保护信号被SCADA 系统打上“全数据判定标记”，此类信号为主站对子站某一时间段内信号的再次唤起，并非故障时刻真实变位信息；

(2) 保护、开关或所属厂站被挂上特定类型标志牌，包括“检修”、 “停运”、“备用”等，在此情况下相应设备所发信号均为非故障信息；

(3) 若信号动作次数超过最大设定次数，即调控中心监控系统短时间内频繁收到同一开关的多次分合闸动作信号，则该信号为无效变位信号，并非故障信息．

根据上述原则，从SCADA 数据库中获取相应信息构成输入输出样本．

2.2 样本扩充方法

实际电力系统故障诊断中，若历史数据充足，直接将其作为本文第1 节所提出的深度神经网络训练样本对其进行训练．若历史数据不够多，本文采用样本扩充策略获得可用于神经网络训练的足够多的样本，从而实现神经网络的训练．

由于电力系统严格的设备入网检测制度、定期检修制度以及严格的人员运行操作及培训制度，同类型的设备只要通过了入网检测，均可认为其质量及性能是满足要求的，其差异在工程上可忽略，同一地区的厂站其地理位置相距都很近，相应其微环境也是相似的，而严格的人员运行操作及培训制度使得所有厂站的人为因素导致的故障也类似，上述这些因素是影响设备动作正确性的主要因素，因此可以将某一设备的历史记录根据需要逐渐扩充至同厂站、临近厂站及地区同类型的设备历史记录，相应所获得的样本足可以反映特定设备的运行特性．

基于上述考虑，本文提出了样本扩充的新方法，其基本思路是：先扩展统计与被诊断元件相同或相近的其他元件的历史记录，若所得记录仍然不足，则进一步扩展区域范围，直至同类型设备的历史记录足够；然后基于历史记录统计各信号出错概率，再通过随机抽样得到需要诊断设备的完整样本．以某变压器为例，具体样本扩充方法如下．

步骤1提取该变压器的故障历史记录．

步骤2若记录不足，继续提取同厂站内相同型号、相同配置、装设时间相近的其他变压器的历史故障记录；否则，样本扩充结束．

步骤3若其样本数量仍不足，将搜索范围进一步扩大至相邻厂站、同地区同电压等级其他厂站直至获取足够历史记录，或尽可能多地获得样本；否则，样本扩充结束．

步骤4若依然无法获得足够记录作为神经网络训练数据，则采用基于概率经抽样扩充策略，以获取足够多的训练样本．具体如下：根据已获取的样本量，对于遥信信号，分别计算出输入向量中每个属性在相应设备故障与无故障情况下取1 的概率；否则，样本扩充结束．计算方法为

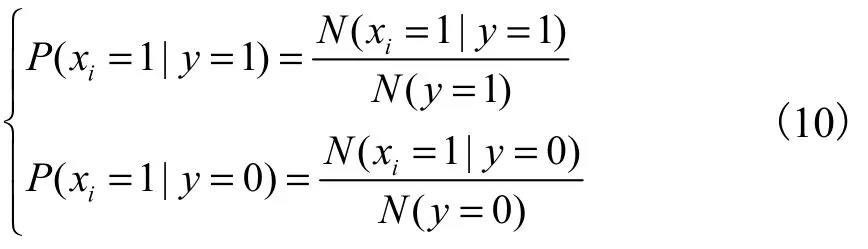
式中：N(y=1)、N (y=0)分别表示获取的样本中设备故障、无故障样本的数量；P (xi=1|y= 1)表示故障时接收到相应有效遥信信号的概率；P (xi=1|y= 0)表示未发生故障时接收到相应有效遥信信号的概率．

类似地，对于遥测数据，“功率变化”及“变化前功率为0”两属性的处理与上述方法相同；“最终功率为0”则分别统计故障与无故障情况下潮流发生变化时该属性为1 的概率．

步骤5根据获得的每一位输入的取值概率，采用随机抽样的方法确定样本中的每一位输入xi(i ∈[1, n0])的取值，其具体取值确定方法如下．

(1) 对于元件故障情况，样本标签y=1 ，样本中第i 个输入ix 为

式中ri∈(0,1)为抽样产生的随机数．

(2) 类似地，对于设备无故障情况，样本标签y= 0，样本特征 xi为

类似地，对于“最终功率为0”属性分两种情况讨论：①潮流未发生变化时，该属性与变化前潮流为0 相等；②潮流发生变化时，用随机抽样的方法确定属性取值．

步骤6将样本标签与得到的特征值拼接组成长向量作为一条完整样本．

步骤7重复步骤5，直至获得故障与无故障样本至少各2 000 条，并与SCADA 数据库中的样本共同构成样本集用于网络训练．

对于其他类型的被诊断元件，均可采用类似方法获得足够数据对第1 节所述网络模型进行训练．

3 算例分析

考虑输电线路故障为电力系统故障中的典型故障之一，且输电线路故障发生次数较多，相应保护、断路器等配置较复杂，故本文以输电线路为例进行了两方面的验证，首先进行样本生成及基于此样本对于网络训练学习正确性的验证；进而把本文所构建的故障诊断模型用于某一实际系统的故障诊断，进一步验证本文诊断模型工程应用的可行性和有效性．用于实验的计算机配置为：Inter®core™i3-4160 CPU @3.60 GHz；已安装内存(RAM)4.0 GB．

3.1 概率诊断模型正确性验证

用第2.2 节步骤5 和步骤6 所述方法生成设备故障与无故障时的样本，然后用模拟样本对本文所构建的故障诊断全连接Logistic 回归深度神经网络(Logistic regression deep neural network，L-R-DNN)进行训练，以验证其概率学习能力．

3.1.1 模拟样本生成

样本设置同表1，样本生成相关概率如表3 所示．训练集、测试集、验证集的故障和无故障样本数量如表4 所示．

表3 中故障情况及无故障情况分别表示被诊断元件实际上发生或未发生故障，对应概率表示该情况下调度中心收到相应信号的概率．

表3 样本生成相关概率Tab.3 Correlation probabilities of sample generation

表4 各样本集样本数量(模拟)Tab.4 Number of samples in each sample set(simulated)

3.1.2 网络模型结构参数选择

实验用网络结构由网格搜索法确定．对于网络待确定参数——网络隐含层数及各层神经元个数，在一定的取值范围内取多组参数值建立L-R-DNN 网络，并用第3.1.1 节中产生的模拟样本分别进行训练至收敛，其参数设置与测试结果如表5 所示，其中m表示隐含层数，神经元个数表示各隐层神经元个数，如(80，40，20)表示3 层隐层神经元个数分别为80、40 和20 个，损失值表示测试集上损失函数的取值，准确率表示相应测试准确率，标星数值表示隐含层数相同时的最低损失及最高准确率．

由上述测试结果可以看出，当网络隐含层数为3，且各隐层神经元个数分别为(60，30，15)时拥有最小损失值，神经元个数为(40，20，10)时拥有最大准确率，说明对于本问题，适当加深网络结构可比单隐层的浅层网络获得更好的诊断性能．

选用准确率最大时的网络(即神经元个数为(40，20，10))作为模型进行后续诊断测试实验，其训练过程中的测试集与验证集损失函数值如图3 所示．

3.1.3 概率诊断测试

测试样本的理论故障概率由以下过程算得：设输入向量为x，根据贝叶斯公式，可以获得元件故障概率为

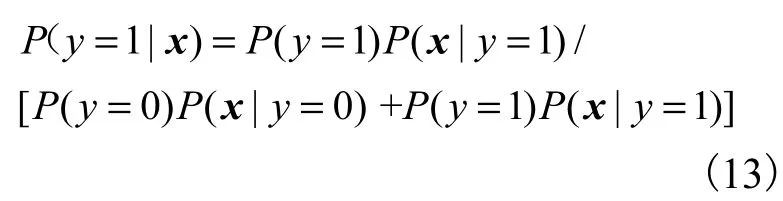
式中P（y=1)、P（y=0)分别表示样本集中相应设备故障与无故障的先验概率，样本集中故障样本与无故障样本数N1、N0均为4 100，则有

P( x|y=0)与 P( x|y=1)分别表示在故障/无故障情况下样本中输入x 的概率，即

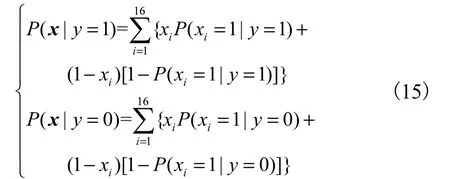
式中ix 表示信号特征向量x 中的第i 个特征位．

用200 条训练样本对模型获取概率特征的能力进行测试．将x 与表3 中设定的概率共同代入式(13)～式(15)可以得到特征向量为x 时被诊断元件发生故障的理论概率P（ y= 1| x)．其他测试样本的选择与计算类似．定义模型输出概率与理论概率间的误差为模型输出概率与计算所得概率之差的绝对值，则模型在测试样本上的平均误差为2.16%．随机选择其中6 条测试样本，其测试样本的输入特征如表6 所示，理论故障概率及网络输出结果如表7 所示.

表6 测试样本的输入特征Tab.6 Input features of the test samples

表7 理论故障概率及网络输出结果Tab.7 Theoretical fault probabilities and outputs of the network

表7 中输入特征即信号特征向量x；理论概率即由公式计算所得到的该输入信号所对应的元件发生故障的概率；把信号特征作为L-R-DNN 的输入，相应其输出即为该信号特征的故障诊断概率；误差为理论概率与网络输出之差的绝对值．

由测试结果可看出，网络模型对于测试样本的故障概率预测较为准确，误差均值仅为2.16%，且表7显示抽取的6 条样本的概率误差均小于6%．因此，本文所构建的L-R-DNN 具备较强的数据特征提取与诊断能力，能快速准确地获得元件故障概率．

3.2 基于样本扩充方法的诊断准确率验证

算例采用实际电力系统线路故障数据以验证本文提出的样本扩充方法及故障诊断模型及算法的可行性和有效性．验证思路为：先提取历史记录，然后选择部分记录用于样本扩充和网络模型训练，其余作为待诊断案例用以测试基于本文样本扩充方法及网络训练的L-R-DNN 网络的故障诊断能力；最后将其与浅层神经网络和专家系统方法进行比较以证明本文方法的优越性．

针对线路的诊断以江苏电网的泰州.陵鼓789 线为例，具体过程如下．

步骤 1先提取该线路自身历史记录共1 条．

步骤2将范围扩大至江苏.园东854 线、江苏.鲍严线、泰州.黄钱729 线、江苏.建古922 线等泰州110 kV 线路，共获得历史记录138 条，包括无故障记录76 条和故障记录62 条，并转化成如表1 所示结构的样本．

步骤3抽取故障记录11 条、无故障记录16条，加上目标线路——泰州.陵鼓789 线样本(故障)共28 条样本作为待诊断案例用于测试网络诊断能力，其余样本作为真实历史记录，由样本扩充方法步骤4 统计获得各特征位的相关概率，具体统计结果如表8 所示．

步骤4最后，根据以上概率由样本扩充方法步骤5～7 生成故障、无故障样本各2 000 条，与除去测试样本外的110 条真实记录一同构成训练样本集用于对L-R-DNN 进行训练．训练收敛之后，对于28 条未参与训练的实际样本进行测试，测试、训练样本集中的样本数量如表9 所示，以输出故障概率0.5 作为分界，结果如表10 所示．

表10 中实际故障情况表示样本对应的被诊断元件记录是否真实地发生故障，诊断情况按网络输出大于0.5 为故障，否则为无故障．

表10 采用训练好的L-R-DNN 对线路测试样本进行诊断的结果Tab.10 Diagnostic results of the test samples on a transmission line obtained using the trained L-R-DNN

同样地，参考表5 的结论，建立隐层神经元为80时的浅层神经网络作为诊断模型，采用与深度神经网络完全相同数据集进行训练和测试，二者在训练轮次、训练时长、诊断时长、测试准确率、测试误差方面对比如表11 所示．其中测试时长表示网络训练收敛后诊断单个样本所需时间；测试误差表示网络在28个测试样本上输出值与标签的平均差，诊断正确时，测试误差越小表示给出的诊断结果越肯定．

表11 L-R-DNN与浅层神经网络模型结果对比Tab.11 Comparison of the results of the L-R-DNN and shallow neural network models

由表11 可以看出，由于浅层神经网络的神经元较多，训练至收敛所需轮次更多，时间也更长，而在进行诊断时，两者所需时间相同且均非常短，在测试集上的测试准确率都达到100%，但L-R-DNN 的测试误差更小．因此，无论从训练所需时间还是诊断误差上来看，本文方法均比浅层神经网络具备更好的性能．需要指出的是，本文输入层信息只是SCADA 信息，并没有考虑其他如PMU 信息及巨大的样本数量(随着样本的累积，其数量将会越来越大)，可以预期，若进一步增加其他信息及样本数量，本文模型相对于浅层模型的优势将越发明显．

相对于神经网络方法，当前多家电力公司采用的专家系统方法诊断流程为：先根据专家经验建立规则库，再根据故障特征，对照规则进行诊断．具体地，其对于线路的故障认定逻辑大致可总结为“本侧保护动作与本侧开关变位”或 “线路本侧开关变位与线路对侧开关变位”，基于此规则对上述测试样本进行诊断，得到诊断结果如表12 所示．

表12 采用专家系统对线路测试样本的诊断结果Tab.12 Diagnostic results of the test samples on a transmission line obtained using the expert system

从表10 可以看出，本文构建的L-R-DNN 模型在测试样本上的测试准确率为100%，而表12 为当前电力公司应用的专家系统诊断方法对上述测试样本的诊断结果，有5 个无故障样本被错误地诊断为故障样本，误辨率高达31.25%．此结果证明了本文方法相对于目前广泛采用的专家系统而言明显地降低了误辨率，相应地，也同时证明了本文所构建的L-RDNN 及相应的样本扩展方法的有效性及正确性．