一种描述强对流三维流场的非刚性曲面匹配方法

王 萍，顾 恺，侯谨毅

(天津大学电气自动化与信息工程学院，天津 300072)

强对流天气目前是指伴随雷暴现象的对流性大风(风速≥17.2 m/s)、冰雹、短时强降水等．强对流天气发生于中小尺度天气系统，空间尺度小，其生命史短暂并带有明显的突发性，较短的仅有几分钟至一小时[1]. 虽然强对流天气发生的时间短，但是破坏力却非常强，它会引发洪涝、滑坡、泥石流等自然灾害，致使房倒屋毁、植被作物受灾、电信交通中断甚至人员伤亡等，因此分析和预报强对流天气对国民经济、民众安全有着重要意义．强对流天气是由空气剧烈垂直运动导致的，以上升和下沉气流为主．描述出包含上升和下沉气流的三维流场有助于对强对流天气的分析.

对强对流天气的分析基本都依赖多普勒天气雷达数据．多普勒天气雷达作为一种有效、及时的观测手段，时间、空间分辨率较高，推动了短时临近预报的发展，也是研究中小尺度天气系统的重要资料来源．随着全国天气雷达布网的完善，雷达资料产品在天气预报分析领域扮演着越来越重要的角色，新一代多普勒天气雷达所采集到的是各仰角上的圆锥面上的信息[2]，传统的强对流分析方法都是基于各仰角上的雷达数据进行的，这对于由空气强烈的垂直运动引发的强对流天气而言，空间垂直维度连续性信息的欠缺使分析效果受到限制．

目前，国内外一些科研人员主要通过三维风场反演来达到描述强对流三维流场的目的．1975 年，Ray等[3]较早提出双雷达风场反演的直接合成法ODD(over determined dual-Doppler)技术，反演出了龙卷云的三维风场结构；1998 年，Bousquet 等[4]在ODD 技术的基础上又提出了EODD(extended ODD)技术；2012 年，罗昌荣等[5]将双雷达反演方法普遍采用的笛卡尔坐标系改为地球坐标系，并通过质量连续方程，以及迭代的方法进行估算从而使用双雷达反演三维风场．总之，通过三雷达或双雷达的反演效果较好，但仅仅局限于多雷达探测范围重叠的区域．因此也有些研究者尝试通过单雷达反演三维风场：1991年，Sun 等[6]提出一种全四维变分法，以Boussinesq模型为预报模型，具有反演三维风场和热力场的能力；庄子波等[7]提出了VAD 方法，但是VAD 方法对垂直速度的估计不准确．总之，若仅使用单雷达进行三维风场反演，由于信息有限，反演的结果精确度有限，且计算复杂度较高．

如果有一种较为简捷的方法，能够达到描述强对流三维流场的效果，那么不仅可以详细、具体地表现出强对流天气过程中各个时刻流场中气流的情况，还有助于预报员分析强对流的发展趋势，为强对流天气的预报提供依据．

本文基于多普勒天气雷达基数据，对雷达基数据进行双线性插值的预处理．设置反射率因子阈值，获得反射率因子大于等于阈值的三维格点数据，对三维格点数据通过 Marching Cubes 方法进行曲面重建．基于相邻体扫时刻同一数据点的反射率因子基本不变的假设，设计了一种非刚性的、基于特征融合的曲面匹配方法，对相邻体扫时刻的曲面间进行曲面匹配．通过曲面匹配可获得三维流场中各数据点的位移向量，从而近似描述出强对流天气的三维流场．最后，通过模拟数据进行曲面匹配方法的效果测试．

1 数据准备

新一代多普勒天气雷达扫描所采集到的是圆锥面上的信息[2]，扫描方式如图1 所示．对于多普勒雷达的VCP21 体扫模式[8]，雷达在6 min 间隔下扫描9个仰角，获取9 个仰角上的圆锥面数据．其中9 个仰角具体为 0.5°、1.5°、2.4°、3.4°、4.3°、6.0°、9.9°、14.6°、19.5°．实际上，预报员分析所依赖的雷达图(如图2 所示)就是这些仰角上圆锥面的俯视平面图．

图1 多普勒雷达扫描示意Fig.1 Schematic of Doppler radar scanning

图2 雷达反射率因子回波Fig.2 Echo of radar reflectivity factor

对于同一组体扫数据的9 张锥面图，对应二维水平面上的点，选取不同高度9 个数据中的最大反射率因子合成一张组合反射率图．本文采用的单体分割算法[9]首先根据对流单体从内到外反射率因子强度逐级减弱的分布规律，通过区域生长法得到一系列独立的对流单体核区，再使用膨胀避让算法[9]，自适应地在雷达组合反射率图上分割出对流单体．通过这种方法分割的单体，不受单体尺度、雷达回波强度的限制，也较好地解决了外围相互交织的多单体对象的自适应分割问题．

为了获得对流单体的三维描述，本文利用9 个仰角的反射率因子数据经过双线性插值[10]得到高度分辨率为0.25 km、水平分辨率为1 km×1 km 的70 层平行于水平面的反射率因子数据，雷达射线与对流单体三维格点生成数据的关系如图3 所示．最终得到70 层三维格点数据如图4 所示，它们可以表现出对流单体三维区域几乎每一处的信息，作为本文研究的输入数据．

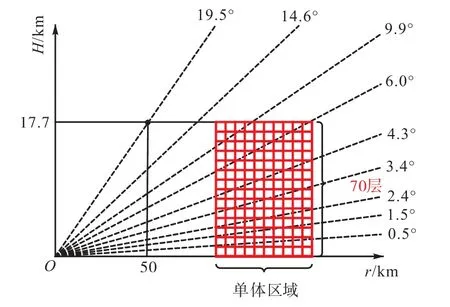
图3 70层水平格点数据与雷达射线的关系示意Fig.3 Schematic of the relationship between 70 layers of horizontal grid data and radar rays

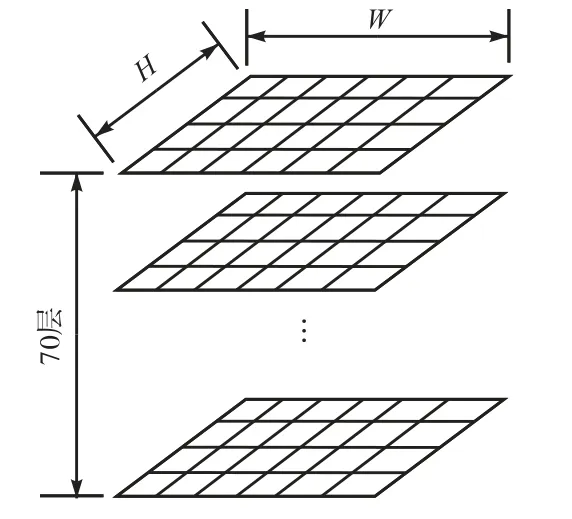
图4 三维格点数据示意Fig.4 Schematic of three-dimensional grid point data

2 曲面重建

2.1 三维点云的获取与去噪

从内到外反射率因子逐层降低的分布特点是对流单体的共性．因此，对于前一节获取的70 层水平格点数据，设定一个反射率因子阈值 Rth后，所有反射率因子大于等于该阈值的三维格点组成了一个实心的点云核．

对于该三维点云核，本文采取半径滤波方法[11]滤除点云中的噪声．具体而言，对于三维点云数据，如果一个点在设定搜索半径r范围内的邻近点数量小于给定的阈值t，则判断该点为远离主体点云的稀疏离群点，做删除处理．经过测试与统计分析，设置r为3 个单位长度，阈值t为3．

2.2 通过Marching Cubes方法重建曲面

拓扑结构对于点云的匹配、形状分析等应用具有重要作用．而上文提取的空间点云仅仅表示物体的几何形状，无法表达内部拓扑结构．本文采用一种常见的曲面重建方法——Marching Cubes 方法[12]．这种方法本质上是从一个三维空间数据场中抽取出一个等值面．

Marching Cubes 方法采用分治的策略，基本思想是把三维点云中相邻的8 个体元看作一个六面立方体的8 个顶点．对于图4 中H×W×70 的三维格点数据而言，六面立方体个数为(H－1)×(W－1)×69.把每个六面立方体的8 个顶点的值与设定的等值面的阈值进行比较，而每个顶点的值与阈值相比有大于阈值或不大于阈值两种情况，因此一共有28＝256 种情况，可通过建立一个长度为256 的表，供算法查询调用．

图5 对其中15 种典型的情况给出了说明. 对于每个立方体，标记有实心点的顶点表示该点的值大于设定的阈值，其余顶点数值未达到阈值. 以图5 中的2 号子图为例，顶点A是该立方体8 个顶点中唯一大于所设阈值的点，与其相邻的顶点有B、C、D．在AB、AC、AD这3 条线段上，分别根据相应线段的两个顶点的数值做线性插值，找到每条线段上数值等于阈值的点的位置．对于这3 条线段，设线段的端点坐标为1P、2P ，它们的值分别为R1和R2．等值面的阈值为R，P为待求的坐标，其计算式为

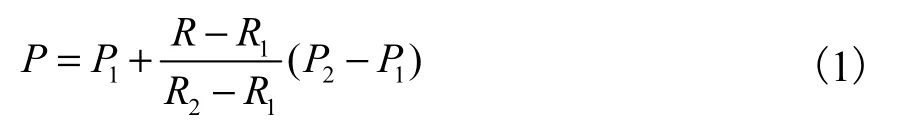
本文曲面重建的具体步骤如下．

步骤1建立长度为256 的索引表．

步骤2对三维格点数据，取出与其相邻的7 个数据格点，构成一个正六面体，然后根据这8 个数据点与设定的等值面的阈值的大小关系，得出对应的索引值．

步骤3根据索引值搜索索引表，得到需要进行插值的边，进而得到三角面．

步骤4遍历所有正六面体，重复步骤2 和步骤3，进而得到所有三角面的输出．

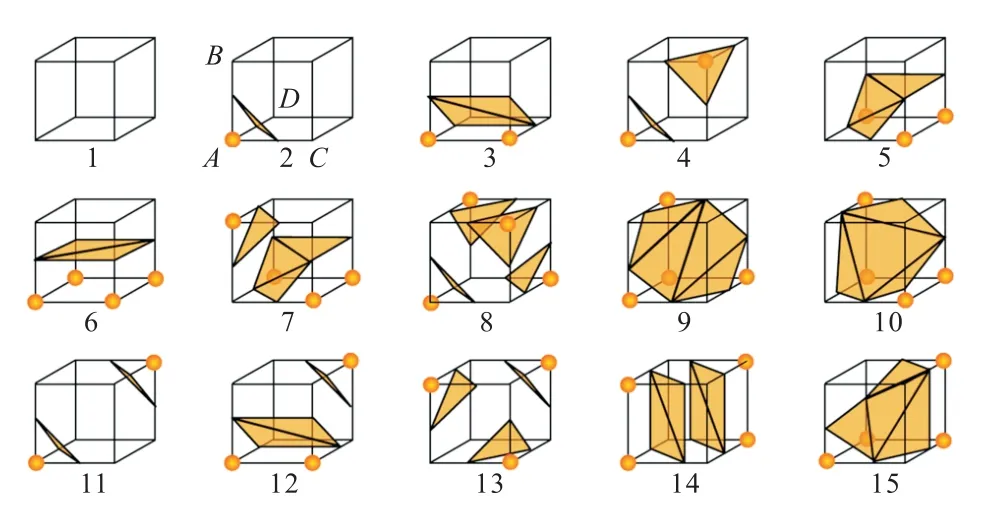
图5 Marching Cubes 15种典型情况示意Fig.5 Schematic of 15 typical Marching Cubes cases

通过以上4 步，把这些生成的面相连就得到了最终的等值面．这种方法就好像移动立方块一样，Marching Cubes 算法因此得名．总的来说，Marching Cubes 算法原理简单、效果较好．图 6 是通过Marching Cubes 算法对对流单体点云数据重建表面的一个示例．

图6 Marching Cubes重建效果Fig.6 Reconstructed rendering of Marching Cubes

3 非刚性曲面匹配方法设计

曲面匹配是逆向工程的关键技术之一．一般曲面匹配是通过求解一个刚性坐标变换矩阵(对于三维空间，空间变换矩阵是4×4 的)，将不同三维数据点集统一到一个坐标系下．最为常见的曲面匹配方法为基于最小二乘原理进行多次迭代的ICP(iterative closest point)方法[13]，该类方法的最终目标是求解出两个曲面间最佳的刚性坐标变换矩阵．因此主要适用于两个外形完全一致的曲面，如不同摄像头视角下的同一物体．但是本文涉及的前后时刻反射率因子大于设定阈值的三维格点重建的一组曲面形状虽然相似但并非完全一致，为此本文设计了一种精确至点到点、非刚性的曲面匹配方法．

3.1 曲面点特征向量设计

三维曲面上各点的法向量指的是垂直于该点切平面的向量，通过三维曲面上某点的法向量，可以获得该点处局部曲面的朝向信息．另外，曲率是曲面弯曲程度的一种度量，是一种重要的曲面局部特征，通过三维曲面上某点的曲率，可以得到该点处局部曲面的凹凸信息．综合曲面上一点的法向量与曲率两种信息，就可以相当程度上描述出该点处的曲面特征．本文具体的法向量与曲率的求法如下所述．

1) 曲面点的法向量

面模型是由一定数目的面片来逼近的，面片越多则面模型越精细．对于各面片的法向量，通过组成各面片的任意两条边的叉乘向量并单位化来表示．这里以三角形面片为例，给出具体计算方法．设图7 中的F是一个三角形面片，P0( x0, y0, z0)、P1( x1, y1, z1)、P2( x2, y2, z2)是这三角形面片的3 个顶点．G是F所在平面．n为位于P0处的该三角形面片的法向量，则有

图7 三角形面片法向量求解示意Fig.7 Schematic of normal vector solution for triangular patch

对于曲面任意点P的法向量，设为该点周围所有面片的法向量的平均．假设NP为该点周围面片数，in 为该点周围第i个面片的法向量，nP为P点的法向量，则有

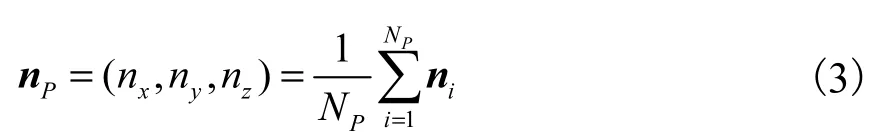
向量示意如图8 所示．

2) 曲面点的曲率

曲面上某一点的曲率，是基于该点法向量进行求解的．经过曲面上点P的法线(法向量)的某一平面与曲面相交可得到一条曲线，这条曲线在点P处的曲率即为曲面上的点P的曲率，如图9 所示．经过顶点P的法线的平面可以有无数个(可任意旋转)，这也意味着相交的曲线也有无数条，而每条曲线在顶点P都有一个曲率．设所有这些曲率中最大的曲率为κH，最小的曲率为κL．其他常见曲率如高斯曲率、平均曲率基于最大曲率和最小曲率求得．最大曲率与最小曲率求法分别为

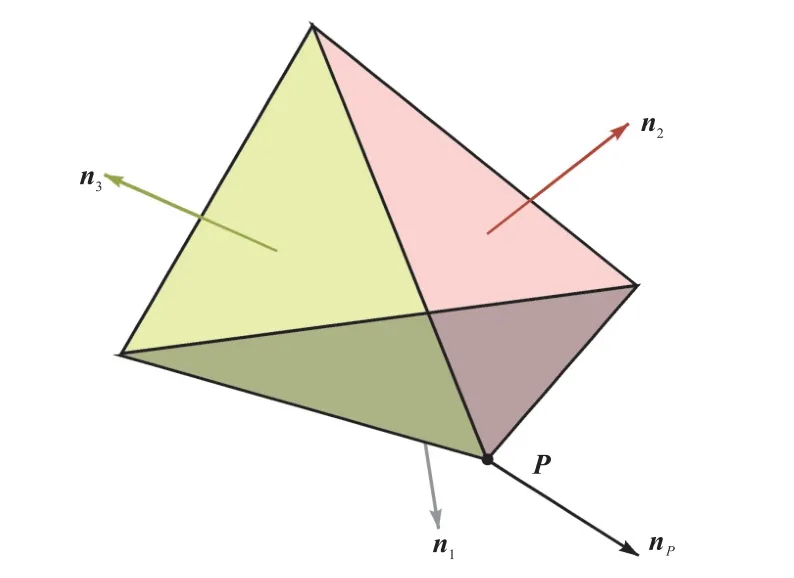
图8 通过P点周围面片法向量求解该点法向量示意Fig.8 Schematic for calculating the normal vector of point P by the normal vectors of the surrounding sur-faces

图9 曲面曲率示意Fig.9 Schematic of surface curvature

综上，曲面上某一点的法向量nP=( nx, ny, nz)代表该处的朝向，曲率又代表了该处的凹凸程度．本文把法向量与最大、最小曲率进行融合[14-15]，形成一个5 维的特征向量，以表示曲面上某一点的形状信息，即

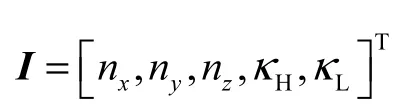
考虑到这个特征向量I 的5 元素量纲并不一致，为了消除各参数量纲的影响，本文对法向量进行单位化处理，对最大、最小曲率进行归一化处理．具体公式分别为

式中：为所有特征向量中最大曲率κH的平均值；为所有特征向量中最大曲率κH的最大值；为所有特征向量中最大曲率κH的最小值；为所有特征向量的最小曲率κL的平均值；为所有特征向量中最小曲率κL的最大值；为所有特征向量中最小曲率κL的最小值．通过式(7)～(11)，原特征向量I变为新的特征向量其各元素的模值均不超过1，消除了量纲的影响．

3.2 匹配区域的限定与“相对坐标向量”

在使用特征向量进行曲面匹配时，还需要限定匹配区域．例如，对于单体曲面东南角的某点，它不应该与下一时刻单体曲面西北角的某点匹配，即便它们的5 维特征向量非常相似．所以对于曲面上的每一点，除了该点处曲面的形状和朝向信息外，还应考虑该点在曲面的位置信息来限定匹配区域．对于每个点，它们都有一个3 维空间的坐标，可以通过这个3维坐标来直接表示出一个点的位置信息．然而，对流单体内部的气流不仅有上升与下沉的运动，还有幅度更大的东南西北方向的水平移动，对于同一降水目标物粒子，它在相邻体扫时刻下的两个位置的3 维坐标可能相差很大，因此直接用3 维空间的坐标来表示位置信息并不能很好地达到匹配区域限定的目的．

为了解决这个问题，本文提出了一种新的位置信息表达方法，以达到表示某点在3 维曲面上的“相对位置”的效果．假设反射率因子大于等于设定阈值的3 维格点的外边界曲面包含的外边界点有N 个．在如图10 所示的以单体框为底面、垂直地面向上的射线作为z 轴建立的坐标系下，设曲面上的点P的坐标为( xP, yP, zP)．对于这N 个外边界点，坐标x 小于 xP的点的个数设为Nx，坐标y 小于 yP的点的个数设为Ny，坐标z 小于 zP的点的个数设为Nz．进而用3 维向量作为一种新的坐标信息表达方式，并称之为顶点P在重建曲面上的“相对坐标向量”．以曲面最高点为例(假设最高点唯一)，那么它的“相对坐标向量”中的第 3 维的值为(N－1)/N．“相对坐标向量”很好地表现了一个点在曲面上的相对位置．对于空气中同一个降水物粒子而言，虽然它在相邻体扫时刻间隔时间内位移的绝对距离可能很大，但它在重建表面上的相对位置变化应该较小，同时，“相对坐标向量”变化也会较小．通过多次

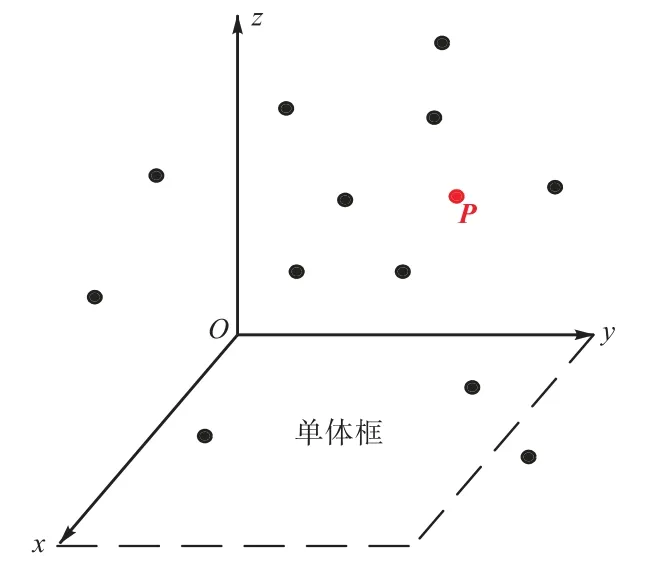
图10 三维笛卡尔坐标系与曲面上的点Fig.10 Three-dimensional Cartesian coordinate system and points on surface

3.3 相似性度量的选择

对于不同点的特征向量，评价它们的相似性程度时，需要用到相似性度量．常见的相似性度量[16]有欧氏距离、曼哈顿距离、切比雪夫距离、马氏距离、余弦相似度等等．本文选择欧式距离．

考虑到对于前一时刻曲面上的点P，后一时刻曲面上可能有多个点的5 维特征向量与P的5 维特征向量间的欧式距离都很小甚至相同的情况，构建附加匹配条件如下：设前一体扫时刻曲面上的点为P，设后一时刻曲面上与点P的5 维特征向量之间的欧氏距离最小的点为Q1，欧式距离次近的点为Q2，即当最近欧式距离与次近欧式距离的比值小于设定阈值时，才认为这两点组成点对是匹配的．这里的阈值设为0.5(即

3.4 方法流程

综合第3.1、3.2、3.3 节，本文提出的曲面匹配方法的具体步骤可以总结如下．

步骤1前一时刻的曲面选取一点P并作标记，求它的5 维特征向量以及“相对坐标向量”．

步骤2对后一时刻的曲面，限定匹配区域为“相对坐标向量”与P相差10%以内的区域．

步骤3在后一时刻的曲面的限定匹配区域下，通过遍历找出与P点的5 维特征向量间欧式距离最近的点1Q以及次近点2Q ．

步骤4判断欧式最近距离与次近距离的比值是否小于设定阈值(本文取为0.5)，如果小于0.5 则把P与Q设为“匹配点对”，否则不建立“匹配点对”. 然后返回步骤1，步骤1 选取点时跳过所有已标记的点.

不停地迭代以上步骤，直至遍历完前一时刻曲面上的所有点．

通过上述步骤就获得了前一时刻点云重建曲面上的点在下一时刻对应的匹配点，前后时刻点之间的坐标差就被认定是大气中这些降水物粒子的位移向量，用以反映气流场中的气流流向．

3.5 三维流场的描述

通过本文提出的曲面匹配方法，可以得到前一时刻曲面的所有外边界点在下一时刻的匹配点，前后时刻点之间的坐标差就是大气中粒子的位移向量．将这些位移向量通过可视化函数库VTK 进行3 维可视化，如图11 所示，其中每个箭头的起点代表了前一体扫时刻的曲面上的某一点P的位置，箭头的末端(尖头处)代表后一体扫时刻的曲面上与点P组成“匹配点对”的点Q．箭头代表了在一个体扫时刻间隔(6 min)内点P到点Q的相对位移．由此就获得了这个曲面上所有点在时间间隔6 min 内的位移，并获得强对流三维流场的近似描述．

图11 位移向量三维可视化示意Fig.11 Schematic of three-dimensional visualization of displacement vectors

具体地，可令上升箭头为白色，下沉箭头为黑色，这样可以很清晰地、定性地观察出流场各处上升与下沉气流的情况，如图12 所示．通过对这些箭头(向量)进行求均值、计数等数据处理，也可以定量地表示出当前时刻流场整体的上升与下沉气流的对比．

另外，在雷达径向速度图中，正速度指的是在雷达波束的径向上远离雷达(即径向速度为正)，一般用红色等暖色表示；负速度指的是在雷达波束的径向上靠近雷达(即径向速度为负)，一般用绿色等冷色表示．相应地，也可以通过红色箭头和绿色箭头(对应雷达径向速度图的正速度与负速度)来分别代表径向上远离雷达和靠近雷达的位移向量，如图 13 所示．而位移向量是远离或靠近雷达是通过位移向量与该点到雷达的连接向量(即雷达扫描径线)的点乘的正负判断．

图12 上升、下沉位移向量示意Fig.12 Schematic of rising and sinking displacement vectors

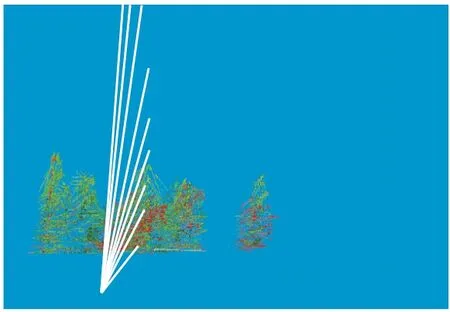
图13 径向正、负位移向量示意Fig.13 Schematic of radial positive and negative displacement vectors

4 曲面匹配效果测试

在实际应用中，对于两个相似但不完全一致的曲面，无法得到客观上“正确”的匹配结果．而如果是对于两个形状一致但角度不同的两个曲面(比如第2 个曲面是由第1 个曲面进行旋转后得到的)，可以知道这两个曲面上点的“正确”的匹配结果，很容易对算法的结果进行评价．比如把通过本文算法得到的正确匹配数除以全部匹配数，得到的百分比值就可以作为一个很好的评价曲面匹配效果标准，称之为“匹配正确率”．因此本文通过模拟数据进行测试，对于一个已知的曲面S，对其施加平移、旋转、缩放、仿射变换后，获得新的曲面T．运用本文方法建立S 与T 的匹配，并统计“匹配正确率”，给出对本文匹配方法的效果评测．

4.1 三维平移变换

将曲面上一点P( x0, y0, z0)在x、y、z 3 个坐标轴方向上分别平移 a、b 和 c，得到一个新的点P′ ( x ′, y ′, z′)．设R为点P到点 P ′的转移矩阵，并设P′=RP，那么4×4 的转移矩阵R为

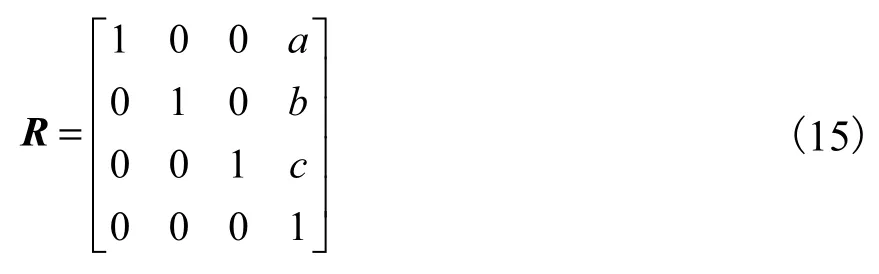
4.2 三维旋转变换

三维空间下的旋转变换为绕某一轴进行旋转，最基本的旋转变换为绕坐标轴x、y、z 的旋转．本文仅通过基本的绕坐标轴的旋转变换来测试曲面匹配效果．设曲面上原本的点为P( x0, y0, z0)，旋转变换后得到的点为P′ ( x′ , y ′, z′)，设P′=RP，绕x、y、z 3 个坐标轴旋转α角的4×4 的变换矩阵分别为Rx、Ry、Rz，如表1 所示．

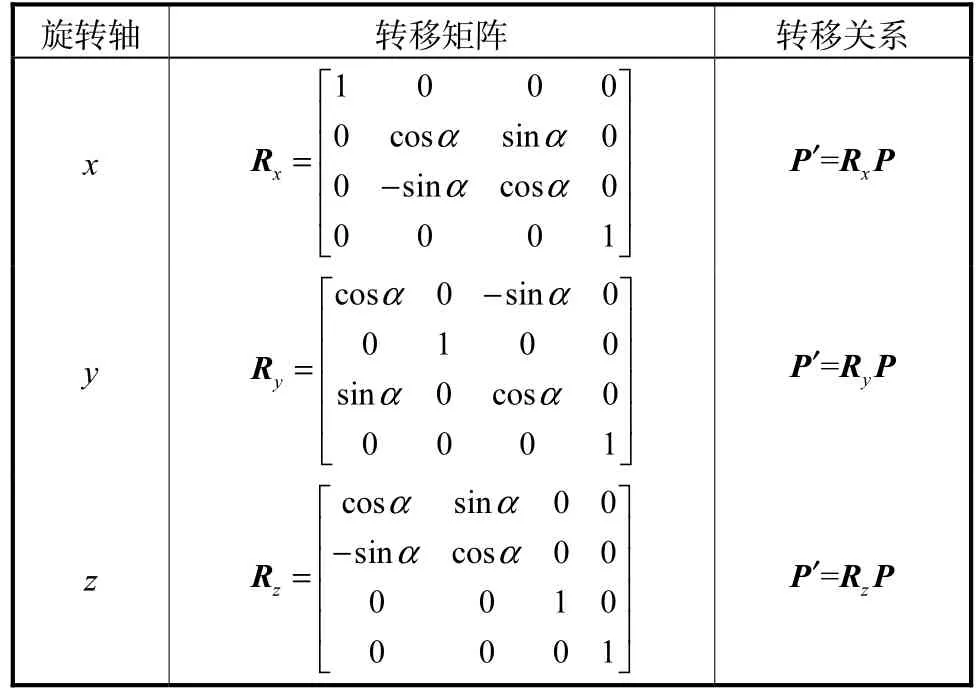
表1 三维基本旋转变换Tab.1 Three-dimensional basic rotation transform

4.3 三维缩放变换

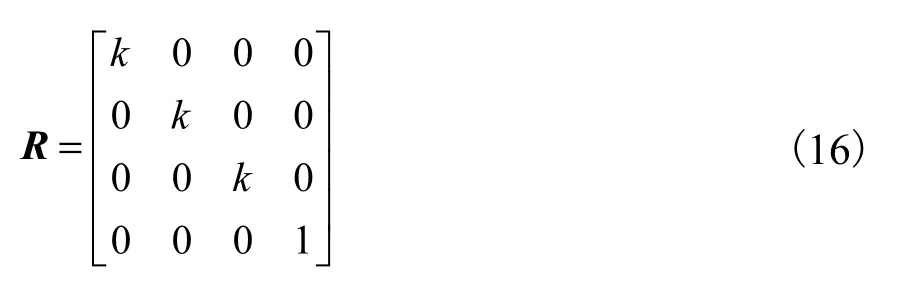
对于曲面而言，进行整体的缩小或放大，设缩小或放大的因数为k．设曲面上原本的点为( x0, y0, z0)，缩放变换后得到的点为P′( x′ , y ′, z′)，设R为点P到点P′的转移矩阵，并设P ′=RP ．那么转移矩阵R的形式为

4.4 三维仿射变换

仿射变换指的是一次非均匀的(即不是缩放变换)线性变换加上一个平移变换．通过仿射变换，球可以转换为椭球．设P′=RP，三维空间下的仿射变换转移矩阵的形式可以表示为

式中 tx、ty、tz分别为平移变换在x、y、z 3 个坐标轴方向上分别平移的距离．

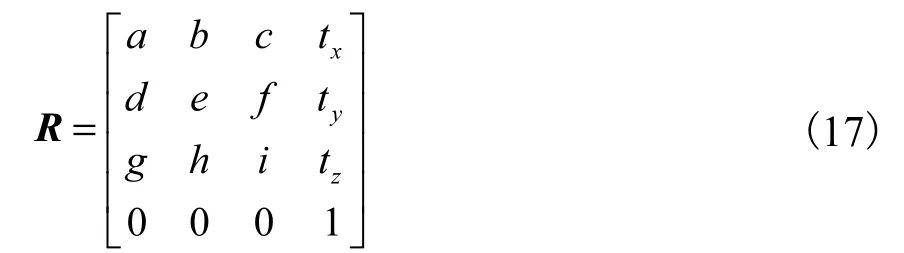
最终，对于各种3 维变换后分别得到的各种曲面Ti与原曲面S 进行匹配，各选取10 组样例，平均匹配正确率如表2 所示．从表2 中可知对于平移变换与缩放变换(表2 的前3 行)，匹配平均正确率分别达到了99.6%、92.0%、89.7%，这是由于这些变换下，曲面的改变相对较小，并且均为刚性变化．而对于旋转变换(表2 的第4 行)，匹配平均正确率为77.6%，匹配正确率较低的原因主要是对于原曲面S 中的一点，经过旋转变换后它的“相对坐标向量”改变较大，导致与之对应的变换后曲面T 上的点可能并不在本文曲面匹配方法限定的匹配区域中，这是本文曲面匹配方法的一个不足之处．对于仿射变换(表2 的第5 行)，匹配平均正确率为76.3%，仿射变换与其他变换相比，形变更大，因此匹配平均正确率最低．最后，对这5 种变换的正确率求平均，综合平均匹配正确率为87.0%．

表2 曲面匹配平均正确率Tab.2 Average accuracies of surface matching cases

5 结 语

本文为了描述强对流天气的三维流场，在相邻体扫时刻同一降水物粒子的反射率因子基本不变的假设下，设定反射率因子阈值，对相邻体扫时刻反射率因子大于等于阈值的点云构建出一组相似但不完全一致的曲面．本文提出了一种新的基于法向量与曲率特征融合、点到点的非刚性曲面匹配的方法，并且设计了“相对坐标向量”进行匹配区域的限制，设置附加条件解决一点对多点匹配的不确定性问题．最后，通过模拟数据进行测试，经测试，本文的曲面匹配方法综合平均正确率达到了87.0%．借助雷达反射率因子数据的插值三维格点数据，通过本文的曲面匹配方法可获得三维流场中各数据点的位移向量，从而近似描述出强对流天气的三维流场．

当然，本文方法尚存在一些不足之处．本文使用的双线性插值方法，随着数据点到雷达间距离的增加，雷达射线变得更稀疏，插值效果也会受到影响，因此本文方法更适用于距离雷达较近的区域，比如水平距离100 km 内．另外，本文方法的计算量较大，可以通过增大反射率因子阈值 Rth或提升硬件配置实现缩减运算时间的效果，如何通过改进曲面匹配方法以提升运算效率值得进一步的研究．