基于Hilbert-Huang 变换的大地电磁去噪研究

陈钧,严良俊,周磊

(1.油气资源与勘探技术教育部重点实验室(长江大学)，湖北 武汉 430100；2.非常规油气省部共建协同创新中心，湖北 武汉 430100)

0 引言

大地电磁在电磁法勘探领域有着广泛的应用，但是其信号弱、易受干扰问题一直难以解决。随着研究的深入发展，国内外大地电磁测深前处理已经取得许多成果，研究者提出的去噪方法种类繁多：胡家华等[1]对大地电磁噪声源进行了分析并认为人文噪声是主要干扰源；王书明等[2-3]比较了大地电磁功率谱和高功率谱，同时对大地电磁信号的统计特征进行了分析。研究者主要利用大地电磁信号和噪声的不同特征对他们加以分离或者根据干扰特征压制噪声：王辉等[4]使用改进的远参考方法对矿区近场源噪声进行压制并且分析了近场源噪声的特点；刘俊峰等[5]引入了一种多结构元素组成的滤波器用于消除大地电磁信号噪声；李晋等[6]运用递归分析的方法进行了大地电磁信号的信号和噪声识别，然后对噪声进行压制。本文采用的HHT方法是根据噪声和信号的时频谱特征将它们加以分离。

随着人文活动的加剧，许多以往的数据处理方式已不能有效压制近场源效应，所获数据与后续工作的精度要求不符。如何有效压制近场效应已经成了大地电磁测深技术前处理的一个重要研究方向。在近场效应下，视电阻率曲线表现为一条斜率 45°的线段，相位曲线则为 0°(对数坐标)[4]。近年来，Hilbert-Huang 变换在处理数据的实践中得到广泛应用：Huang等[7]将HHT应用于地球物理并且阐述了HHT相比其他处理方法在处理非线性信号上的优越性；白大为等[8]将HHT方法应用于带天然气水合物勘探中提取反射信号；杨洋等[9]将HHT解析包络的思想结合小波变换提出一种新的CSEM信号噪声评价方法；蔡剑华、汤井田等[10-11]也先后将HHT应用于大地电磁噪声压制。在验证去噪效果方面，U.Weckmann等[12]提出根据电磁场强极化和响应函数的误差分布来检验去噪效果的方法，他提出正常含噪声较少信号的分布函数应该是趋近于高斯分布的，并且使用大量的实际数据验证了该观点。

本文把HHT与加拿大凤凰公司的SSMT2000系统相结合，应用到某处实地采集的大地电磁测深数据中，并研究了HHT对近场干扰的压制效果。在介绍HHT原理的基础上，先数值模拟了经验模态分解(EMD)，确认了其对复杂信号的处理能力之后，进一步对采集到的大地电磁数据电磁各道进行分解，根据希尔伯特时频谱对信号筛选去噪，最后再结合SSMT2000的计算结果和去噪前后的电磁场极化方向的响应函数分布情况进行验证。

1 方法原理

Huang等人提出的HHT变换扩大了Hilbert Transform的适用范围，它分为两个部分：经验模态分解(EMD)和Hilbert spectrum分析。Huang利用信号的频率特征，根据波峰波谷的包络线在时间尺度上对信号进行分解，指出1个IMF必须满足以下2个条件：①在整个IMF数据序列中，极值点和零点的数量差应当不超过1个；②在任何时间点上，由信号序列局部最大值定义的包络和局部极小值定义的包络，两者的均值必须为零。满足以上2个条件的IMF 已被实践证明适用于 Hilbert 变换[7]。

用程序进行EMD分解流程大致如下。

1)初始信号X(t)0先用插值(一般用三次样条插值)后数据找到波峰值、波谷值，保存波峰、波谷横坐标和波峰、波谷值。

2)对波峰、波谷进行插值(一般用三次样条插值)，因此产生上下包络线并保存。

3)用循环语句将插值后的每个点的波峰、波谷信号求和再除以2，即得到均值信号(记为mik)，并保存在一个新数组中。

4)计算原始信号和mik的差值，记为hik：hik=X(t)-mik。如果hik符合基本面模式分量的条件，就作为第i个IMF输出保存：sj=hik；如果不满足条件，就对hik继续前三步。

5)令此时的原始信号减去hik，得到剩余信号ri：ri=X(t)i-sj。将ri作为初始信号继续进行上面步骤，得到不同的IMF和剩余信号ri，直到剩余信号ri不再有波峰或波谷时，分解结束。

图1给出了程序流程。流程中第四步有一个筛选判断，一般情况下设定一个停止准则(本文使用毛炜等提出的准则3)[13]：

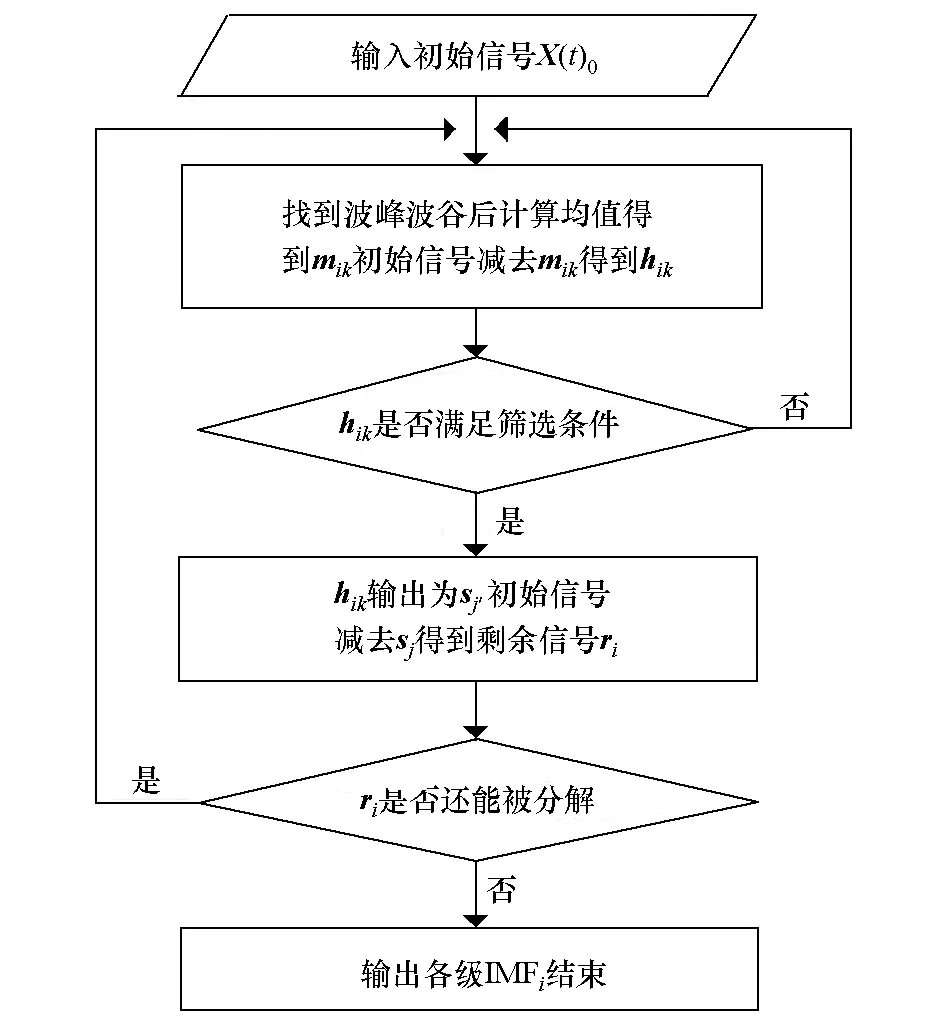
图1 EMD流程

(1)

最后可以得到

(2)

式中：sj(t)为各个IMF，rn(t)为残余分解量。

筛选后对剩余的各个IMF分量进行Hilbert变换：

(3)

式(3)中：ai(t)、φi(t)是IMF分量的时变幅度和相位，rn(t)一般不进行Hilbert变换。在传统的傅里叶分析中，为了定义局部频率值起码需要一个完整的周期。对于非线性非平稳信号傅氏变换不够准确，于是Huang等人根据Hilbert-Huang变换提出了新的瞬时频率定义方法：

(4)

式中N为IMF个数。式(4)可以表示每一个IMF的瞬时频率。根据前文给出的瞬时频率定义，可以把原始信号(式(3))表示为

(5)

式(5)中实部是Hilbert谱，一般记为H(ω,t)。

Hilbert 边际谱：

H(ω,t)=Re[x(t)]，

(6)

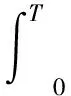
(7)

式中：T是总信号跨度；h(ω)为Hilbert边际谱，即H(ω,t)做时间积分可得到Hilbert边际谱。

2 经验模态分解数值模拟：

以模拟信号y=x+1.5sin(5x)+sin(20x)为例进行EMD分解，该信号的频率由15 s内的0.8 Hz和3.2 Hz这2个正弦电场信号和1个线性电场信号组成，对它进行分解。图2a是原始电场信号，图2b—d中的蓝色信号是分解得到的固有模态函数IMF1-2和剩余信号，橙色线为构成原始电场信号的正确信号分量。显然，图中IMF1对应3.2 Hz正弦信号，IMF2对应 0.8 Hz正弦信号，而剩余分量则是对应线性信号。由于端点效应数据在端点处少量数据点不拟合，从模拟中也能发现经验模态分解对信号的分解和还原都很成功。

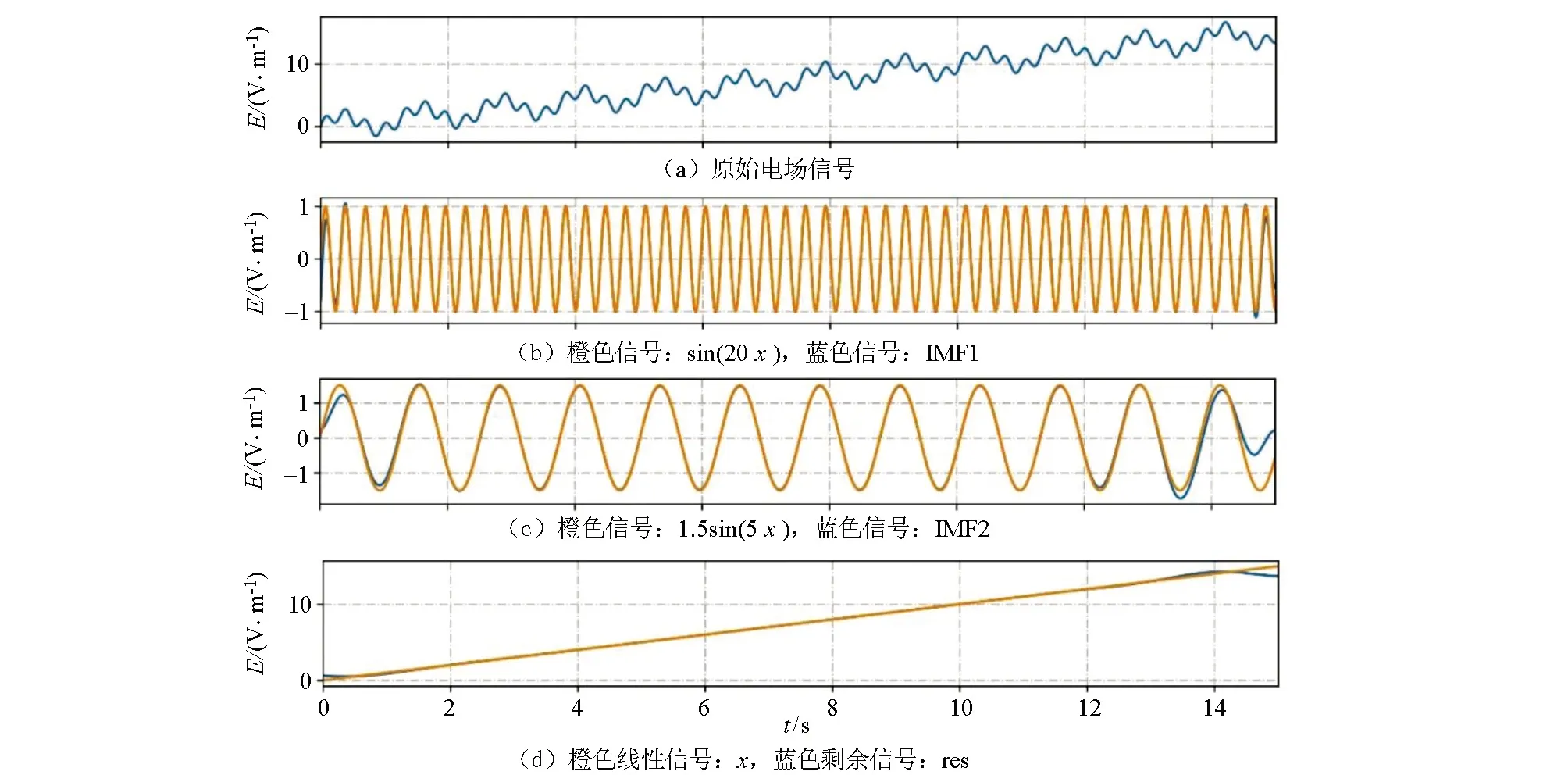
图2 数值模拟模拟经验模态分解

在对模拟信号分解重构成功的基础上再对该信号添加一个锯齿波干扰模拟噪声(图3)，继续验证EMD分解。图4显示分离出的IMF5和添加的锯齿波干扰十分接近，而剩余信号res是分解剩余的线性信号(见图3)，可见EMD分解成功，压制了锯齿波噪声。

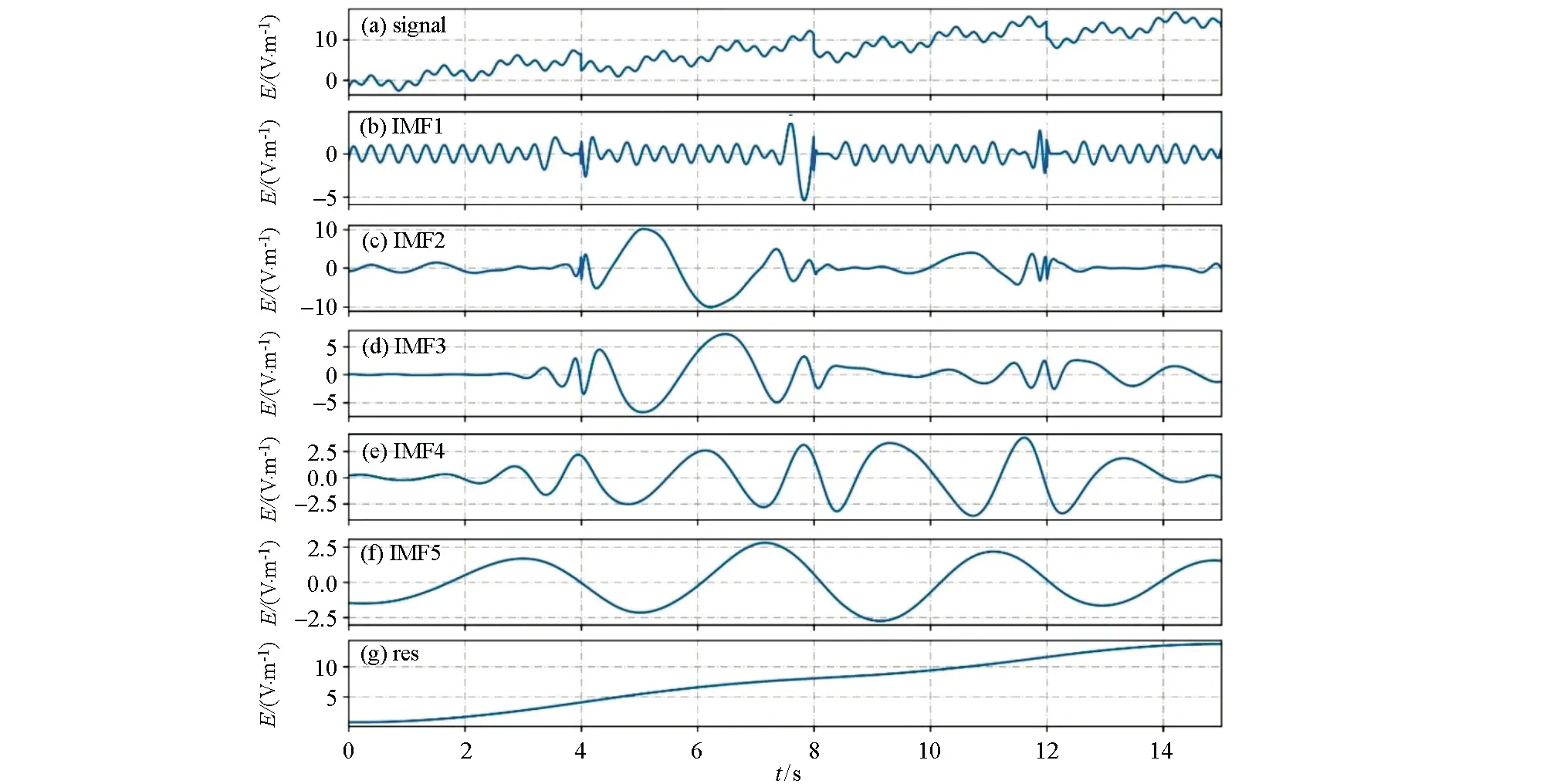
a—加入噪声后的电场信号;b～f—IMF1～IMF5;g—剩余信号

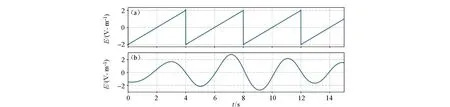
图4 实际噪声(noise)信号(a)和分离的噪声(IMF5)信号(b)

3 实际资料处理

为了进一步研究HHT对大地电磁信号近场干扰的压制效果，以加拿大凤凰公司V8大地电磁测深系统实测采集的大地电磁测深数据为例进行验证。该仪器采集数据时记录电道和磁道里面Ex、Ey、Hx、Hy、Hz5个分量，并将数据以二进制形式储存。使用长江大学严良俊老师课题组开发的ts view软件将采集到的tsn文件转化为csv文件(从二进制编码装换到ASCII码)，用程序对其进行去噪处理后再将文件替换回tsn文件。

已知对于任意1组正交的电磁场水平分量Ex、Hy和Ey、Hx，有波阻抗关系：

(10)

根据阻抗将卡尼亚视电阻率求出。本文使用了甘肃某地采集的大地电磁测深数据，同时使用加拿大凤凰公司的V8测深系统进行视电阻率和功率谱的自动筛选，由于其计算过程在SSMT2000软件里面进行，故在此直接展示计算结果。

采集地区地势较平坦空旷。观察视电阻率曲线(图5)，发现TM信号在1～0.1 Hz时曲线呈现出45°形态，同时这一频段的相位曲线趋近于0°(相位散点图中负的相位加了180°使TE、TM模式下的相位都处于0～180°内)，TM曲线的视电阻率和相位表现出明显的近场干扰效应；观测电磁场极化方向响应函数的分布(图6)，发现分布函数的高斯性被严重破坏，电场磁场散点高度聚集，说明信号受到很大的噪声干扰污染。这些现象表明该数据的TM曲线受到严重的近场干扰。

图5 未去噪时间序列对应的死频带视电阻率和相位曲线

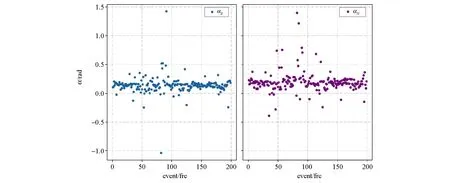
图6 未去噪时的极化方向响应函数

将V8测深系统的3个不同采用频率ts3-ts5(2 400、150、15 Hz)各5道信号(Ex、Hy、Ey、Hx、Hz)分别导出，针对连续采样的ts5以及含较多噪声频段的ts4加以处理。得到各阶IMF之后，利用式(4)对各个IMF进行希尔伯特变换求其瞬时频率，然后根据Hilbert时频谱筛选IMF重构信号(图7)。希尔伯特时频谱刻画的是瞬时频率，噪声频率含量较少的IMF散点会表现出比较连续而不是离散的形态。

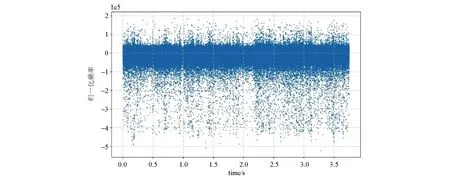
图7 噪声频率含量较多IMF的希尔伯特时频谱

完成噪声压制工作后将重构的信号写回二进制。使用SSMT2000计算视电阻率和相位(图8、图9)并与图5、图6进行了对比。图8显示近场干扰得到了有效压制，其中相位散点图中负的相位加了180°，使得TE、TM模式下的相位都处于0°～180°内，经过HHT方法压制后视电阻率曲线和相位曲线不再表现出近场干扰特征；图9显示散点趋势趋近于高斯分布，说明经过HHT处理后电场、磁场的极化响应函数高斯性已经得到较大修复。以上结果表明Hilbert-Huang变换可以对强近场干扰有效压制。

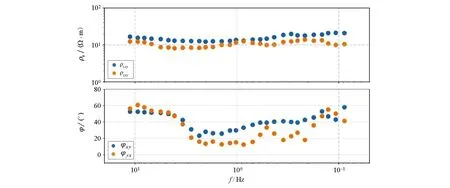
图8 去噪之后重新计算的视电阻率和相位

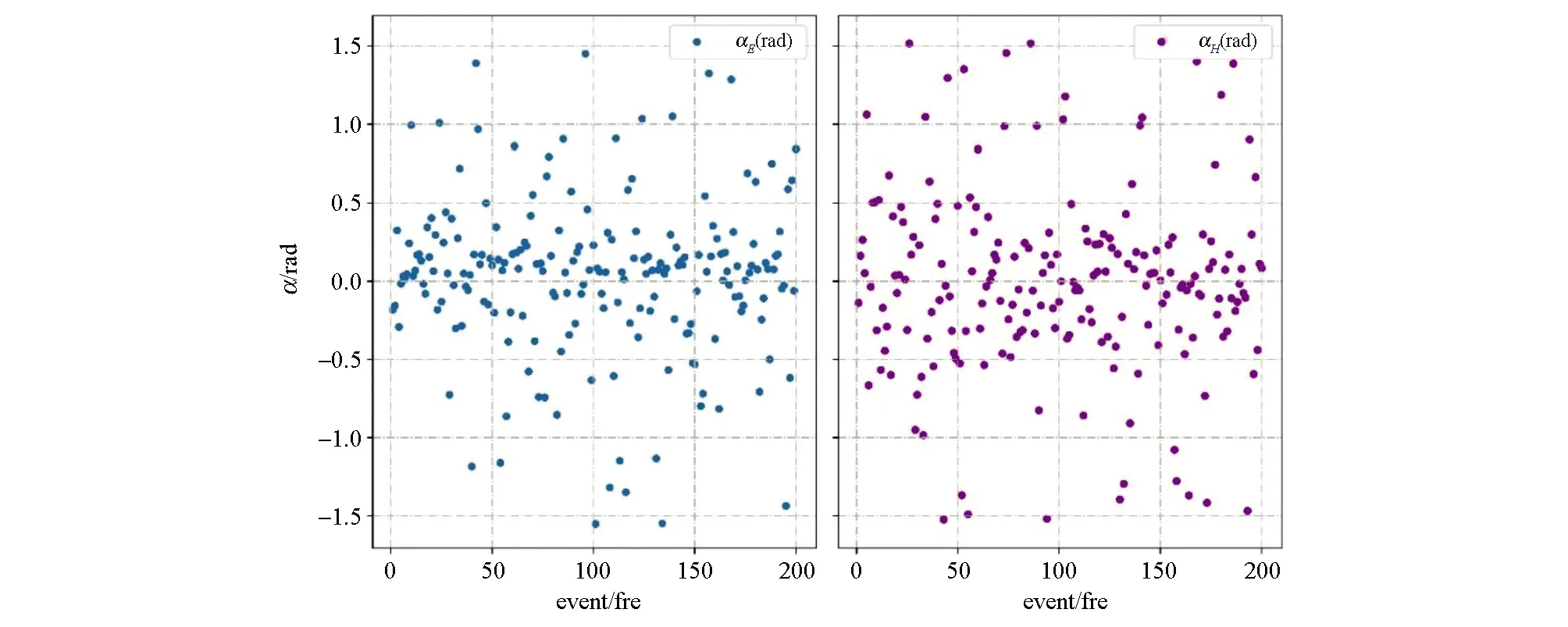
图9 去噪后的极化方向响应函数

4 结论

文中数值模拟了电磁信号的分解重构，针对添加了锯齿波干扰的模拟信号分解重构，成功压制了大部分锯齿波干扰，同时保证了重构波形的准确性，并总结探究了经验模态分解的适用性。

研究发现：对于非线性复杂混合信号，经验模态分解可以将信号分解成简单的固有模态信号，根据希尔伯特边际谱和时频谱很容易区分噪声(IMF1-2)和其余部分的有用信号(其余信号和剩余信号等)，而且相比于传统的傅氏变换，经验模态分解对非稳态非线性信号有着更好的表现。此外，传统远参考方法难以压制1 Hz和0.1 Hz附近的近场干扰噪声，而使用V8测深系统自带的Robust系统结合Hilbert-Huang变换可以有效压制近场噪声。

在处理信号过程中，发现处理后的信号有部分低频数据丢失，视电阻率和相位的功率谱不够平滑连续，人工筛选信号重构也可能造成有效信号丢失并且工作效率不高。如何有针对性地精确去噪、减少有效信号的丢失，是下一步研究的方向。