无伸缩缝改造桥梁上部结构受力特性及其简化设计方法

赵立财

（1.台湾科技大学营建工程系，中国台北 10607； 2.中铁十九局集团第三工程有限公司，沈阳 110136）

无伸缩缝改造桥梁取消了桥梁伸缩缝，根本性地解决了由于桥梁伸缩装置引起的一系列病害，使其成为一种很具吸引力的桥型方案. 但是，无伸缩缝改造桥梁的上部结构和下部结构通过桥台整体浇筑成一体，导致了主梁在承受外界作用下产生的任何一个微小的伸缩变形都将传递到下部结构，影响桩基础的受力性能，而桩基础结构的设计又反过来影响上部主梁结构的受力性能. 李嘉等［1］提出利用结构与土相互作用原理，可较好地得出无伸缩缝改造桥梁结构受力性能，可有效解决工程设计带来的技术难题. 因此，有必要对无伸缩缝改造桥梁进行简化设计，降低无伸缩缝改造桥梁的设计难度. 国外学者对无伸缩缝改造桥梁进行了大量的受力分析，有学者提出普通桥的上部结构的常规设计足以适应由无伸缩缝改造桥梁温度荷载引起任何作用［2］. 在美国早期的调查［3］中发现，一部分州已经编制了内部手册供设计人员查用，其中佛蒙特州大多数整体桥都采用了简化设计计算准则［4］.

本文基于3 m×20 m先简支后连续的小箱梁桥为工程背景，采用无伸缩缝改造桥梁的概念进行无缝化设计，运用有限元软件，建立考虑结构与土相互作用的有限元分析模型，通过无伸缩缝改造桥梁上部结构安全性验算，提出无伸缩缝改造桥梁上部结构简化设计方法，为工程设计人员的初步设计提供参考.

1 无伸缩缝改造桥梁无缝化设计

该桥上部主梁结构采用3 m×20 m“先简支后连续”的装配式预应力混凝土小箱梁，梁高1.2 m，桥面宽（净）12.5 m+0.5 m×2 m，桥梁总长为67.8 m；桥台处取消伸缩缝和支座，通过现浇混凝土后浇段将桥梁上、下部结构连成整体，桥型总体布置如图1所示. 桥面铺装设置采用10 cm厚的沥青混凝土与12 cm厚的C50混凝土现浇层. 桥台采用桩柱式无缝改造桥梁，桥台下部采用直径为0.8 m的圆形钻孔灌注桩基础；桥墩采用双柱式桥墩，钻孔灌注桩基础直径为1.5 m，设置GYZ 325×55 板式橡胶支座；桥台台后采用密实砂回填. 根据现场地质勘探，桥位工程地质状况为：淤泥、中砂、强风化岩石、中风化岩石，地基土物理力学指标，如表1所示. 将整个桥跨结构间设有伸缩缝的位置，利用具有高黏弹性的橡胶改性沥青混凝土作为填料将原有伸缩缝空隙填充密实，如图2所示.

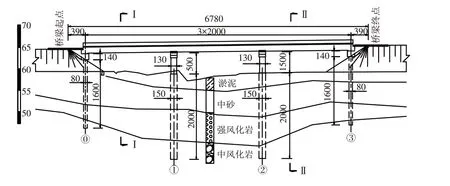
图1 桥型总体布置图（单位：cm）Fig.1 Overall layout of bridge-type（units：cm）

图2 桥跨结构改造成无伸缩缝设计Fig.2 Design of bridge span structure transformed into non-telescopic seam

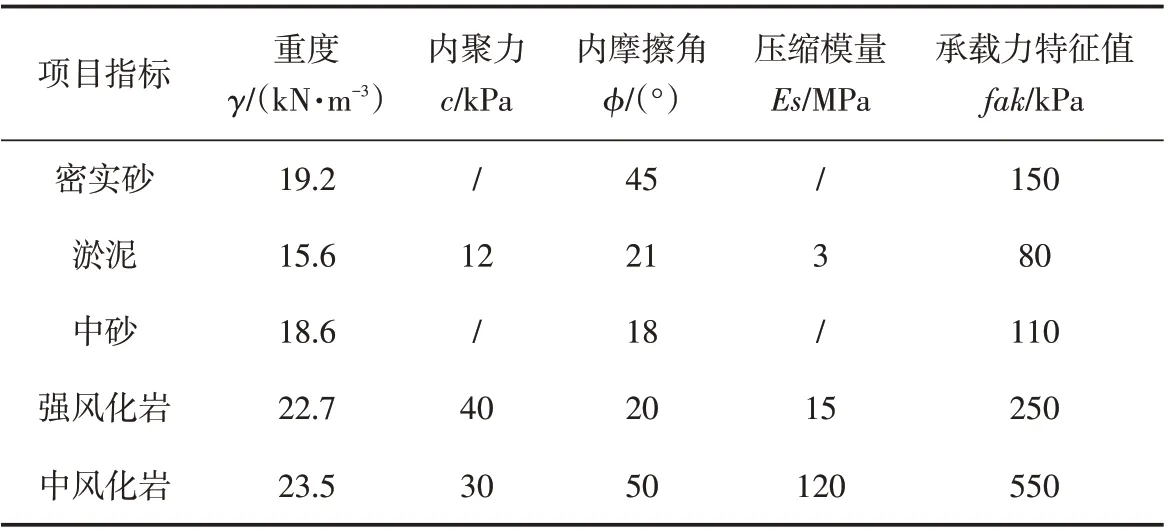
表1 主要地基土物理力学指标建议值表Tab.1 Suggestion values of physical and mechanical indexes of main foundation soil

2 有限元模型

2.1 基本假定

考虑到无伸缩缝改造桥梁和连续小箱梁桥结构受力过程的复杂性，需综合考虑桥梁主梁截面变化、桥梁施工过程等要素，当采用有限元分析软件进行建模时，对计算模型做了如下假定：

1）混凝土桩支承无伸缩缝改造桥梁只考虑桥台及台下桩基础，忽略桥墩以及桥墩下部桩基础的顺桥向方向的抗推刚度影响.

2）采用“梁格法”建立桥梁三维空间有限元模型，不考虑搭板对无伸缩缝改造桥梁的约束影响.

3）桩土相互作用通过“m”法计算侧向土弹簧刚度模拟；假定桩的竖向承载能力满足要求，模型中不考虑桩身与周围土体摩擦接触的影响；箱梁与墩身以固结方式连接，节点单元的抗弯刚度与相邻两侧T梁接头单元的抗弯刚度相同.

4）在等代桩长的理论基础上，建立桥台-土的相互作用的二维弹簧-框架局部模型进行主梁结构性能分析.

2.2 有限元模型建立

2.2.1 模拟方法 本文上部结构采用梁格法进行模拟，主梁、桥墩、桥台和桩基均采用梁单元模拟，桥台与主梁采用刚性连接，墩顶支座采用弹性连接，墩底与基础固结. 模型中的材料参数取值如表2所示，有限元计算模型如图3、图4所示.

表2 材料性质参数Tab.2 Material nature parameter

图3 有限元模型Fig.3 Finite element model

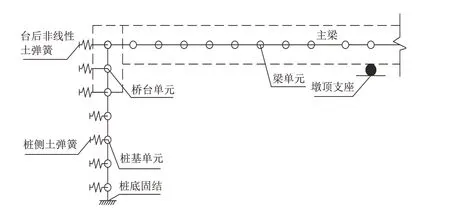
图4 有限元模型简化示意图Fig.4 Simplification schematic drawing of finite element model

2.2.2 台后土弹簧与桩侧土弹簧的确定 台后填土对桥台背墙的作用效应采用非线性土弹簧刚度模拟，弹簧刚度根据美国公路协作规划(NCHRP)147号报告［5］中推荐的K-Δ/H土压力系数曲线进行计算,该计算曲线包含了被动土压力和主动土压力两种情况，并根据侧向土压力系数K值与桥梁顺桥向位移的大小关系将松散、中等密实和密实砂性土三种情况下的NCHRP 曲线数值化. 本文采用密实砂性土（ϕ=45°）压力曲线如图5所示，图中Δ为位移，H为桥台高度，并根据以下公式计算出台后土弹簧刚度：

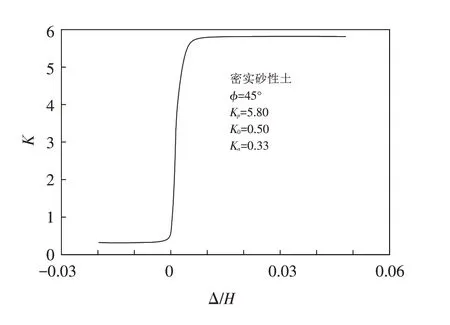
图5 密实砂性土的K-Δ/H压力曲线Fig.5 K-Δ/H pressure curve of dense sand soill

式中：γd为土的干重度；w为有限元计算模型中各节点处的有效宽度；h为有限元计算模型中各节点处的有效高度.

考虑到国内外对于桩土相互作用研究较多，且没有统一的计算方法，本文采用我国《公路桥涵地基与基础设计规范》（JTG D63—2007）规定的“m”法计算桩侧土弹簧刚度，桩底采用固结处理.“m”法将桩基础作为弹性地基梁处理，并根据Winkler假定求解，即桩身任何一点的土抗力大小和该点的水平位移值大小成正比，该方法是我国公路桥梁设计中常使用的一种桩基静力计算方法，详细模拟方法参见文献［6］.

3 无伸缩缝改造桥梁结构安全性验算

本文从工程设计的角度出发，结合相应的桥梁规范对无伸缩缝改造桥梁主梁结构进行安全性验算，验证本文依据相应跨径的常规有伸缩缝桥梁主梁的基本参数来进行无缝化设计的合理性.

3.1 上部结构承载力验算

公路桥梁中预应力混凝土主梁结构的持久状况设计应按承载能力极限状态的要求对结构的承载能力进行计算. 在进行承载能力计算时，作用效应组合采用基本组合，主梁的预应力筋、普通钢筋以及混凝土材料采用其强度设计值. 本文对混凝土桩支承无伸缩缝改造桥梁上部预应力混凝土主梁进行持久状况承载能力极限状态下正截面抗弯承载力验算和斜截面抗剪承载力验算.

3.1.1 上部结构正截面抗弯承载能力验算 无伸缩缝改造桥梁上部结构可按受弯结构进行正截面抗弯承载能力计算. 持久状况正截面抗弯承载能力计算及验算结果见表3. 表中只提取上部主梁结构关键控制截面的计算结果，如：边跨梁端（单元1、2）、边跨1/4跨（单元5）、边跨跨中（单元10）、边跨3/4跨（单元15）、桥墩墩顶（单元21）、中跨1/4跨（单元27）、中跨跨中（单元32），下同.

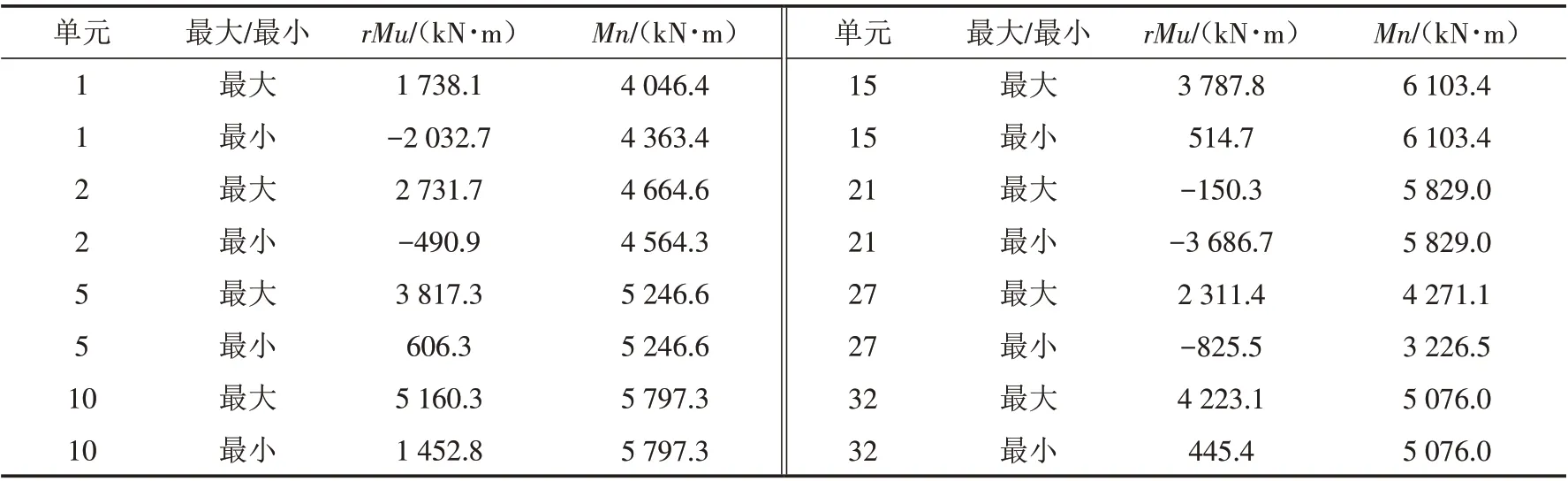
表3 持久状况正截面抗弯承载能力验算Tab.3 Checking calculation of positive cross-sectional anti-bending carrying capacity in permanent condition

由上述验算可知，混凝土桩支承无伸缩缝改造桥梁主梁结构的正截面抗弯承载能力均满足2004年《桥规》［7］要求.

3.1.2 上部结构斜截面抗剪承载能力验算 根据2004年《桥规》第5.27条规定，预应力混凝土主梁结构应进行斜截面的抗剪承载能力验算，并且按照规范中第5.2.9 条规定进行主梁截面尺寸校核. 当满足规范中第5.2.10条规定时，可不进行主梁结构的斜截面抗剪承载能力验算. 本文对混凝土桩支承无缝缝改造桥梁上部结构进行设计时，箍筋采用直径为Ф12的R235钢筋，截面面积取AW=452 mm2，箍筋间距取200 mm. 持久状况下主梁结构斜截面抗剪承载能力验算结果如表4所示.

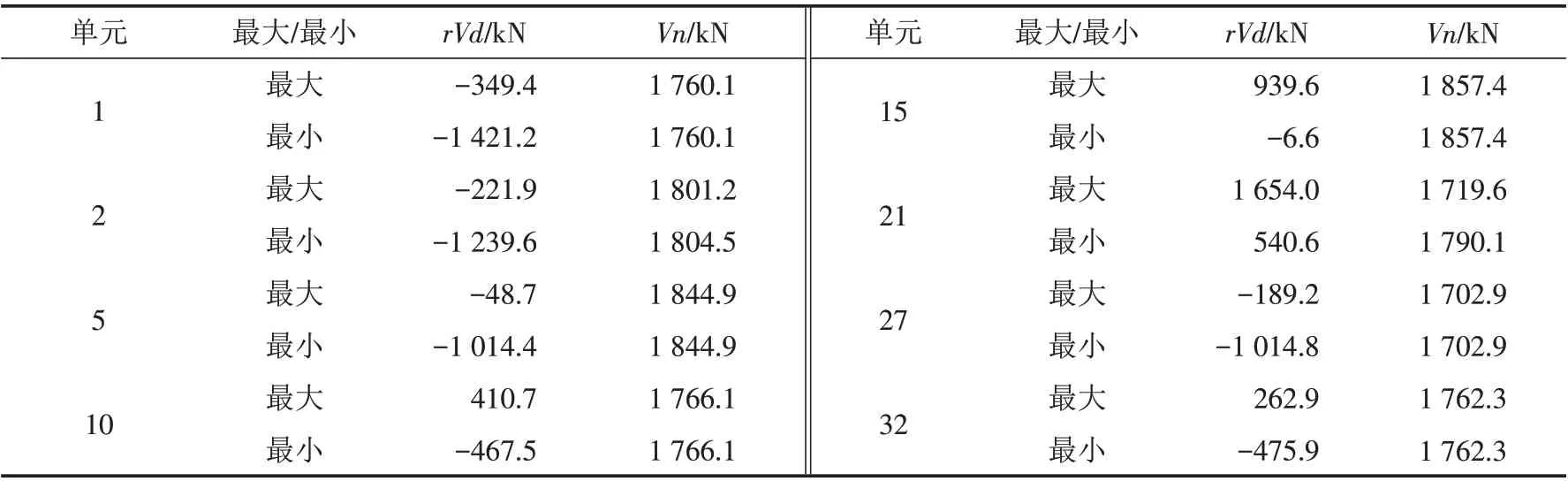
表4 持久状况斜截面抗剪承载能力验算Tab.4 Checking calculation of shear bearing capacity for inclined section under persistent condition

由上述验算可知，混凝土桩支承无伸缩缝改造桥梁主梁结构的斜截面抗剪承载能力均满足2004年《桥规》要求.

3.2 上部结构抗裂验算

公路桥梁中预应力混凝土主梁结构的持久状况设计应按正常使用极限状态的要求，作用效应组合应采用频遇组合、准永久组合以及频遇组合并考虑长期效应组合的三种情况，对结构进行抗裂性验算，并使主梁截面混凝土各项拉应力计算值不超过2004年《桥规》规定的各个相应限值.

根据2004年《桥规》中第6.3条规定，预应力混凝土受弯构件规定须进行正截面抗裂性验算和斜截面抗裂性验算.

由于该无伸缩缝改造桥梁上部主梁结构采用A类预应力混凝土构件，因此在作用效应准永久组合下应满足公式（1）：

在作用效应频遇组合下应满足公式（2）：

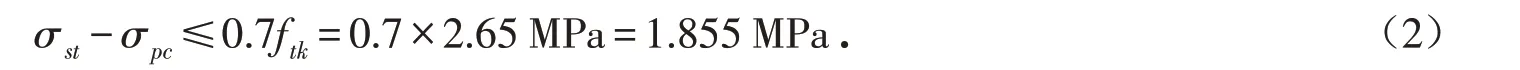
根据表5和图6所示，给出了作用效应准永久组合与频遇组合下，主梁结构正截面的最大拉应力均满足A类预应力混凝土结构截面不能出现拉应力的规定.

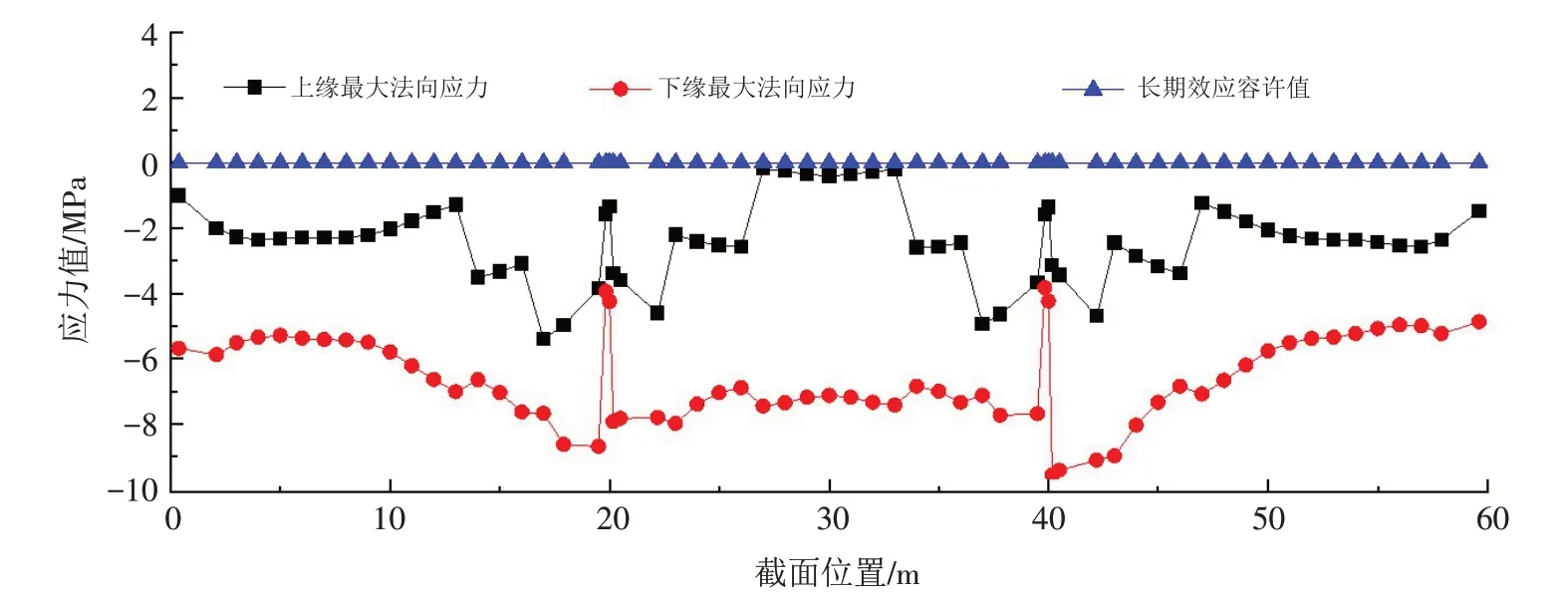
图6 准永久组合下主梁正截面抗裂验算Fig.6 Checking calculation of normal section crack resistance for main beam under quasi-pel manet combination

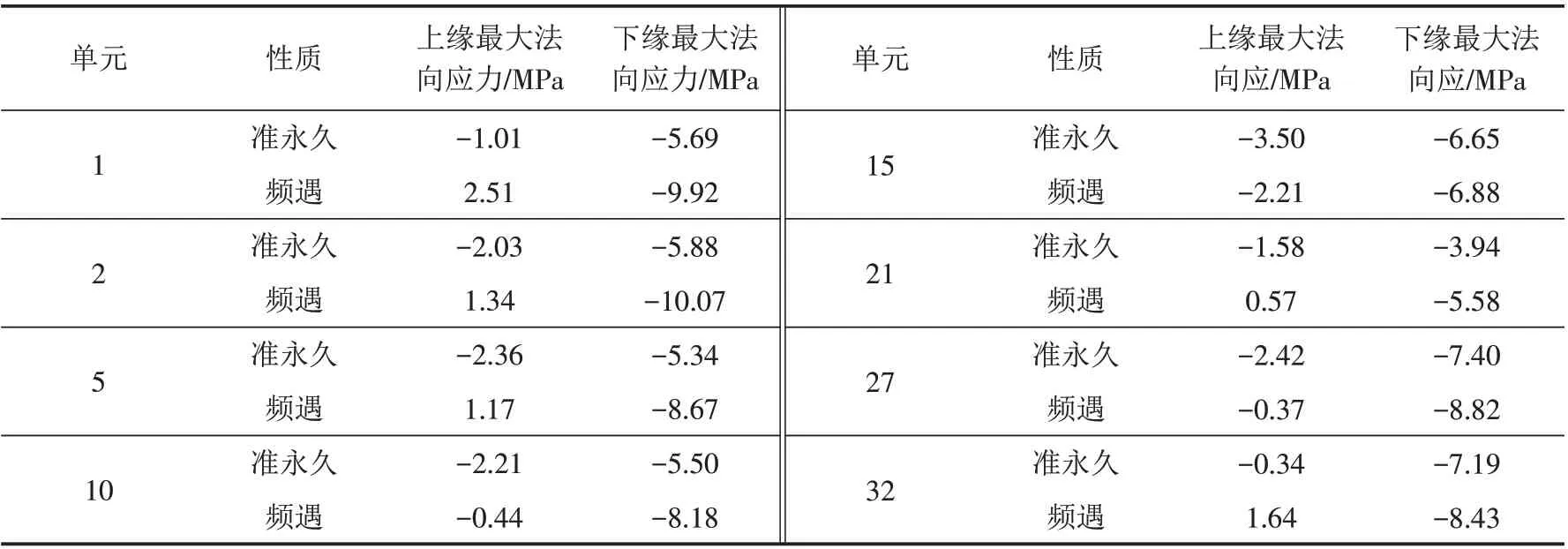
表5 主梁混凝土正截面法向拉应力计算结果Tab.5 Calculation results of normal tensile stress for main beam concrete normal section

根据表5和图7所示，作用效应频遇组合下，除了无伸缩缝改造桥梁桥台处主梁梁端截面（单元1）的上缘拉应力为2.51 MPa，不满足规范规定的要求外，其他截面均未超出拉应力限值1.855 MPa. 预应力混凝土主梁结构的斜截面抗裂性验算，应通过对主梁结构斜截面的主拉应力值σtp进行验算来控制，并应符合公式（3）的要求：

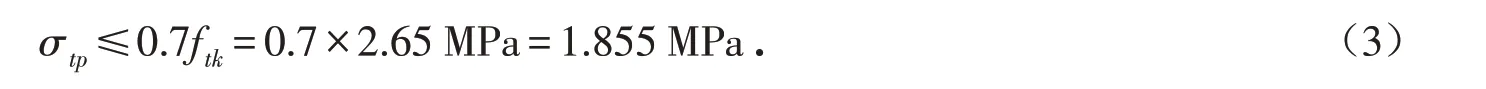
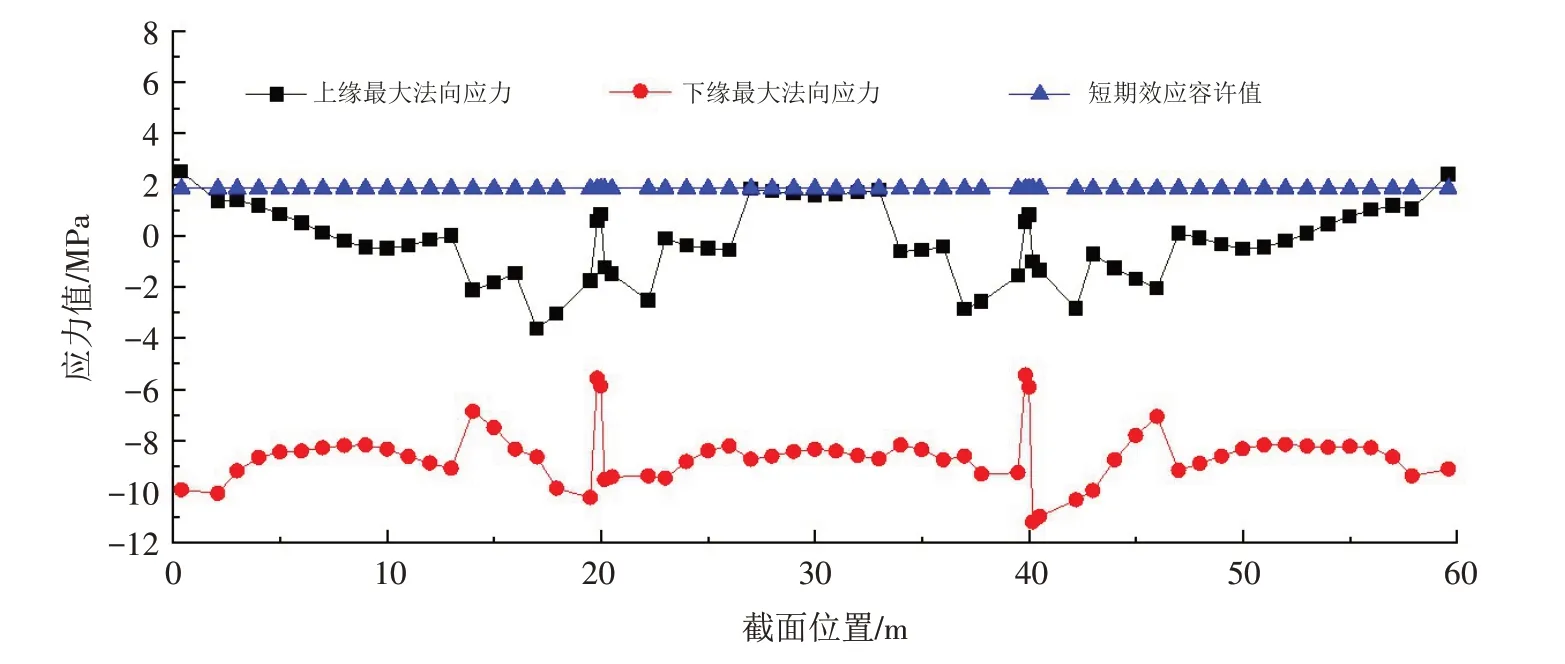
图7 频遇组合下主梁正截面抗裂验算Fig.7 Checking calculation of normal section crack resistance for main beam under frequent combination

根据表6和图8中所示，主梁结构的斜截面最大主拉应力出现在桥台处主梁梁端（单元1）位置，主拉应力为2.75 MPa，大于规范规定的主拉应力限制1.855 MPa，但主梁结构其余截面均能满足规范规定的要求.

表6 主梁混凝土斜截面主拉应力计算结果Tab.6 Calculation results of main tensile stress for concrete inclined section of main beam

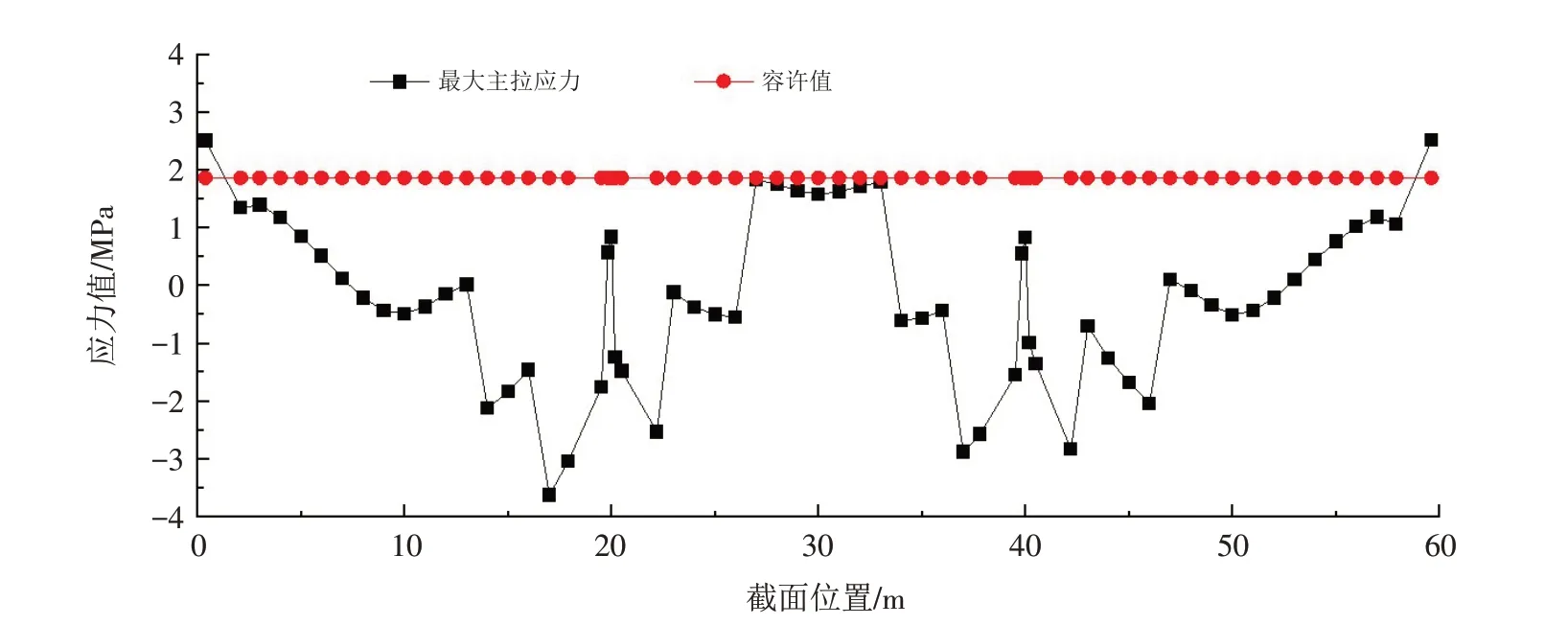
图8 频遇组合下主梁斜截面主拉应力验算Fig.8 Checking calculation of inclined section main tensile stress for main beam under frequent combination

3.3 上部结构应力验算

预应力混凝土主梁结构按持久状况设计时，应对使用阶段主梁结构正截面的法向压应力、斜截面的主压应力和钢筋的拉应力进行计算，并且不得超过规范规定的应力限值，其实质上是对主梁结构进行强度的验算. 而主梁结构的应力验算又可分为持久状况的应力验算和短暂状况的应力验算. 因为混凝土桩支承无伸缩缝改造桥梁上部主梁结构的施工工序与常规“简支转连续”的连续梁桥一致，因此这里不再对无伸缩缝改造桥梁上部主梁结构施工阶段短暂状况的应力进行过多验算［8-9］.

本文主梁结构采用C50混凝土，当施工阶段主梁的混凝土达到设计强度的100%后才能对预应力钢束进行张拉，且主梁结构的预拉区配置有普通钢筋. 根据2004年《桥规》第7.1.5条的规定，则有：

1）受压区混凝土（全预应力、A类）的最大压应力应满足公式（4）：

2）混凝土主压应力应满足公式（5）：

因此，使用阶段A类预应力混凝土主梁结构正截面的法向压应力限值规定为0.5fck=-16.2 MPa，主压应力的限值规定为0.6fck=-19.44 MPa.

使用阶段混凝土桩支承无伸缩缝改造桥梁上部预应力混凝土主梁的正截面混凝土法向压应力和斜截面混凝土主压应力计算结果如表7、表8所示.

表7 使用阶段混凝土正截面法向压应力计算结果Tab.7 Calculation results of normal pressure stress for concrete normal section during use stage

由表7知，主梁结构最大法向压应力出现在桥台处主梁梁端1号单元截面的下缘，法向压应力为-13.01 MPa，小于规范规定的压应力限值-16.2 MPa，因而使用阶段上部主梁结构各截面的正截面法向压应力均满足规范规定的要求，如图9所示.

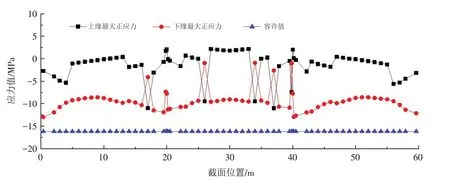
图9 使用阶段混凝土正截面法向压应力计算结果Fig.9 Calculation results of normal pressure stress for concrete normal section during use stage

由表8 可知，主梁结构最大主压应力出现在桥台处主梁梁端2 号单元截面，压应力为-13.05 MPa，小于规范规定的主压应力限值-19.44 MPa，因而使用阶段上部主梁结构各截面的斜截面主压应力均满足规范规定的要求，如图10所示.

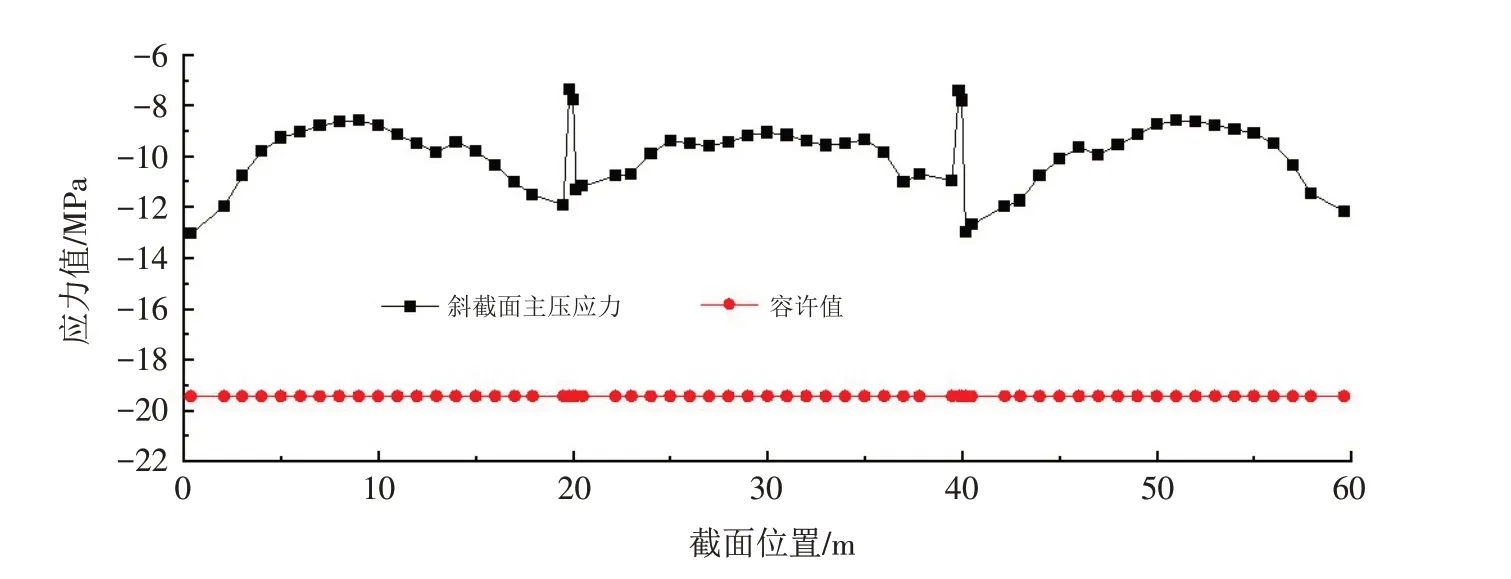
图10 使用阶段混凝土斜截面主压应力计算结果Fig.10 Calculation results of main pressure stress for concrete inclined section during use stage

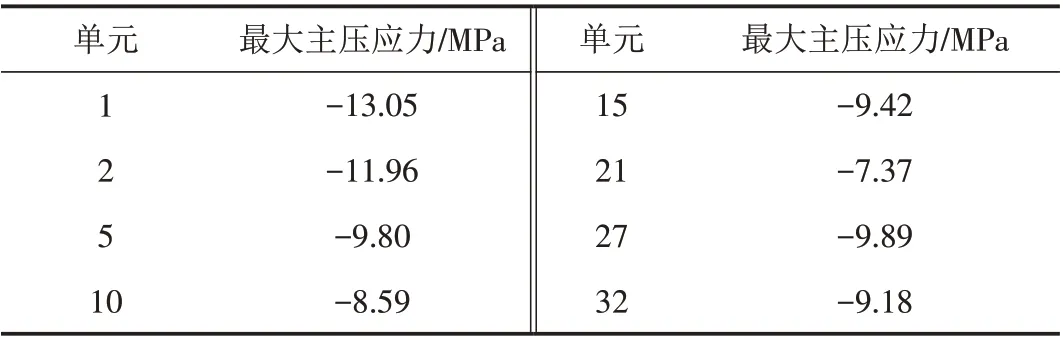
表8 使用阶段混凝土斜截面主压应力计算结果Tab.8 Calculation results of main pressure stress for concrete inclined section during use stage

根据2004年《桥规》中第7.1.5条规定，上部主梁结构的受拉区预应力钢束的最大拉应力应满足公式（6）：

受拉区压应力钢筋的最大拉应力限值按公式（7）计算：

正常使用阶段钢束应力计算如表9所示，因篇幅限值，本文仅给出混凝土桩支承无伸缩缝改造桥梁上部主梁结构的边梁各钢束施工阶段和使用阶段最大应力计算结果，其中张拉控制应力按1395 MPa计算.

由表9可知，钢束最大的拉应力出现在边梁N1钢束，拉应力为1 196.13 MPa，小于规范规定的预应力钢束拉应力限值1209 MPa，故持久状况荷载作用下预应力钢束中的拉应力均满足规范规定的要求.

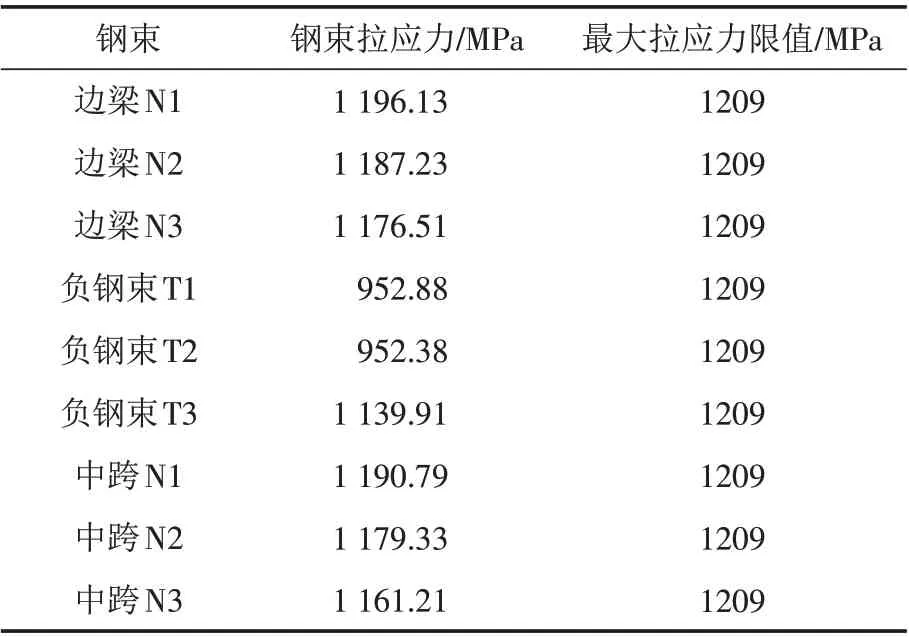
表9 使用阶段预应力钢束拉应力计算结果Tab.9 Calculation results of tensile stress for prestressed steel tendon in usage stage

4 无伸缩缝改造桥梁上部结构简化设计

根据上文对混凝土桩支承无伸缩缝改造桥梁上部结构进行安全性验算可以发现，在进行结构抗裂性验算分析时，无伸缩缝改造桥梁的桥台处主梁梁端不能满足A 类预应力混凝土结构正截面和斜截面的抗裂要求. 其中，当主梁结构在作用短期效应组合下，桥台处主梁梁端截面的上缘出现2.51 MPa的拉应力；当主梁结构进行斜截面抗裂验算时，桥台处主梁梁端主拉应力达到2.75 MPa，均大于规范规定的拉应力限值1.855 MPa. 为了使混凝土桩支承无伸缩缝改造桥梁的主梁设计更加符合其结构受力形式，满足工程设计的要求，本文建议在采用常规有伸缩缝桥梁上部主梁结构参数进行设计的前提下，可以考虑在桥台处主梁的顶板设置预应力钢束T4（图11），以提高无伸缩缝改造桥梁桥台处主梁梁端的截面抗裂能力.

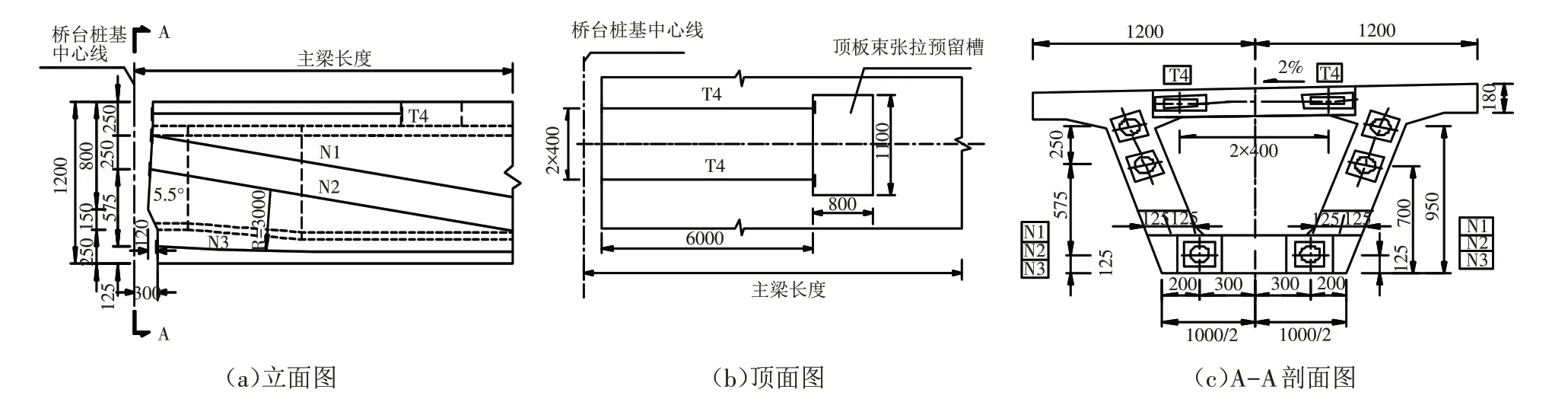
图11 主梁梁端顶板预应力钢束设计（单位：mm）Fig.11 Pre-stressed steel beam design for top plate of main beam end（Unit：mm）

主梁通过采用上述方案设计后，重新对其进行结构安全性验算，结果表明：在满足主梁结构其他设计要求的前提下，主梁的抗裂性能大大地提高. 其中，当主梁结构在作用短期效应组合下，桥台处主梁梁端截面的上缘出现最大的0.72 MPa拉应力，比原主梁结构出现的2.51 MPa拉应力减小了71.3%，且小于主拉应力限值1.855 MPa；当主梁结构进行斜截面抗裂验算时，桥台处主梁梁端主拉应力达1.24 MPa，比原主梁结构出现2.75 MPa拉应力减小了54.6%，且小于主拉应力限值1.855 MPa.

综上所述，桥台处主梁顶板设置预应力钢束T4，有效地解决了混凝土桩支承无伸缩缝改造桥梁主梁因桥台处梁端负弯矩过大引起截面拉应力超过规范规定限值而出现混凝土开裂的问题.

5 结语

本文采用无伸缩缝改造桥梁的概念进行无缝化设计，并对其上部结构进行安全性验算，在此基础上提出了无伸缩缝改造桥梁上部结构简化设计方法，得到以下结论：

1）选择相应跨径的有伸缩缝连续梁桥的主梁结构尺寸进行混凝土桩支承无伸缩缝改造桥梁上部主梁结构设计，基本能满足结构的使用功能. 因此，建议在无伸缩缝改造桥梁设计时，可优先参考相应跨径的连续梁桥的标准图纸，以利于简化无伸缩缝改造桥梁主梁设计时初始参数的选取.

2）针对本文中3 m×20 m的无缝改造桥梁小箱梁桥，对其主梁进行抗裂验算分析时，无伸缩缝改造桥梁的桥台处主梁梁端区域，不能满足预应力混凝土结构正截面抗裂验算和斜截面的抗裂验算. 因此，本文建议在采用常规有伸缩缝桥梁上部主梁结构参数进行设计的前提下，可以考虑在桥台处主梁的顶板区域设置预应力钢束来提高该区域的抗裂能力.