基于电容电压精确计算的MMC环流抑制方法

2021-12-22王静孙谦浩刘国伟赵宇明

电气传动 2021年24期

王静，孙谦浩，刘国伟，赵宇明

（1.深圳供电局有限公司，广东深圳 518020；2.清华大学电机工程与应用电子技术系，北京 100084）

自2010年11月美国Trans Bay Cable直流输电工程的投入运营以来，基于模块化多电平换流器（modular multilevel converter，MMC）的直流输配电技术已经逐渐成为了直流工程领域的新兴力量[1-2]。MMC换流器实现交、直流功率交换的载体是其内部的桥臂环流与子模块电容电压[3-4]。然而，由于拓扑结构的特点与控制方法的实现特性，在传统的控制系统下MMC的桥臂环流中不仅存在着交换有功功率的直流分量，同时存在着多种偶次谐波交流分量，且以二倍频谐波分量为主[5-7]。桥臂环流中的交流分量虽然仅存在于MMC的内部而不会对其外部特性产生明显的影响，但由于增加了桥臂电流的有效值与瞬时值，环流中的交流分量将导致MMC的传输效率降低、器件寿命受到影响，严重时可能危害MMC的运行。因此，实现桥臂环流中交流分量的有效抑制对于保证MMC更高效地运行至关重要[8]。

文献[9-11]对MMC中环流交流分量产生的机理进行了分析，为环流交流分量的抑制提供了理论依据。文献[12-13]提出合理增大桥臂电感的方法来实现对环流交流分量的抑制，然而，桥臂电感的增大不仅会带来损耗、成本以及体积的增加，同时也将降低MMC的动态响应速度。文献[14-15]提出了基于负序旋转坐标的环流抑制方法，但该方法在实际应用中面临着负序分量难以精确捕获的难题。此外，基于坐标变换的方法对三相系统的对称性具有严格的要求，因此该方法的应用具有局限性。文献[16]提出了一种利用桥臂环流交流分量补偿不平衡电压的方法来抑制环流，该方法的不足在于需要增加桥臂电流的测量环节，同时引入了微分计算，降低了MMC系统的稳定性。文献[17-18]将谐振控制器引入了MMC的环流抑制中，但谐振控制的设计复杂，参数计算困难。文献[19]提出了一种基于交叉耦合控制的环流控制方法，但该方法需要增加两个PI控制器，增加了控制系统的运算量与复杂度。文献[20-21]对基于最大电平逼近调制的MMC采用了投入子模块补偿法，从而减小了桥臂环流的交流分量。然而，与文献[16]中所提的环流抑制方法相似，投入子模块补偿法也需要增加额外的测量量，同时增加了调制系统的计算负担，且由于仅适用于最大电平逼近调制策略，该方法的应用具有一定的局限性。

鉴于上述背景，为了更经济、更简洁、更有效、更通用地实现对MMC桥臂环流中交流分量的抑制，本文基于对子模块电容电压的精确计算，提出了一种能够在阀级控制系统内实现桥臂环流交流分量抑制的控制方法，并基于Matlab/Simulink仿真软件对该方法的正确性与有效性进行了验证。

1 传统子模块计算方法下的MMC桥臂环流分析

图1为MMC拓扑结构与传统子模块计算方法下的控制系统总体架构。

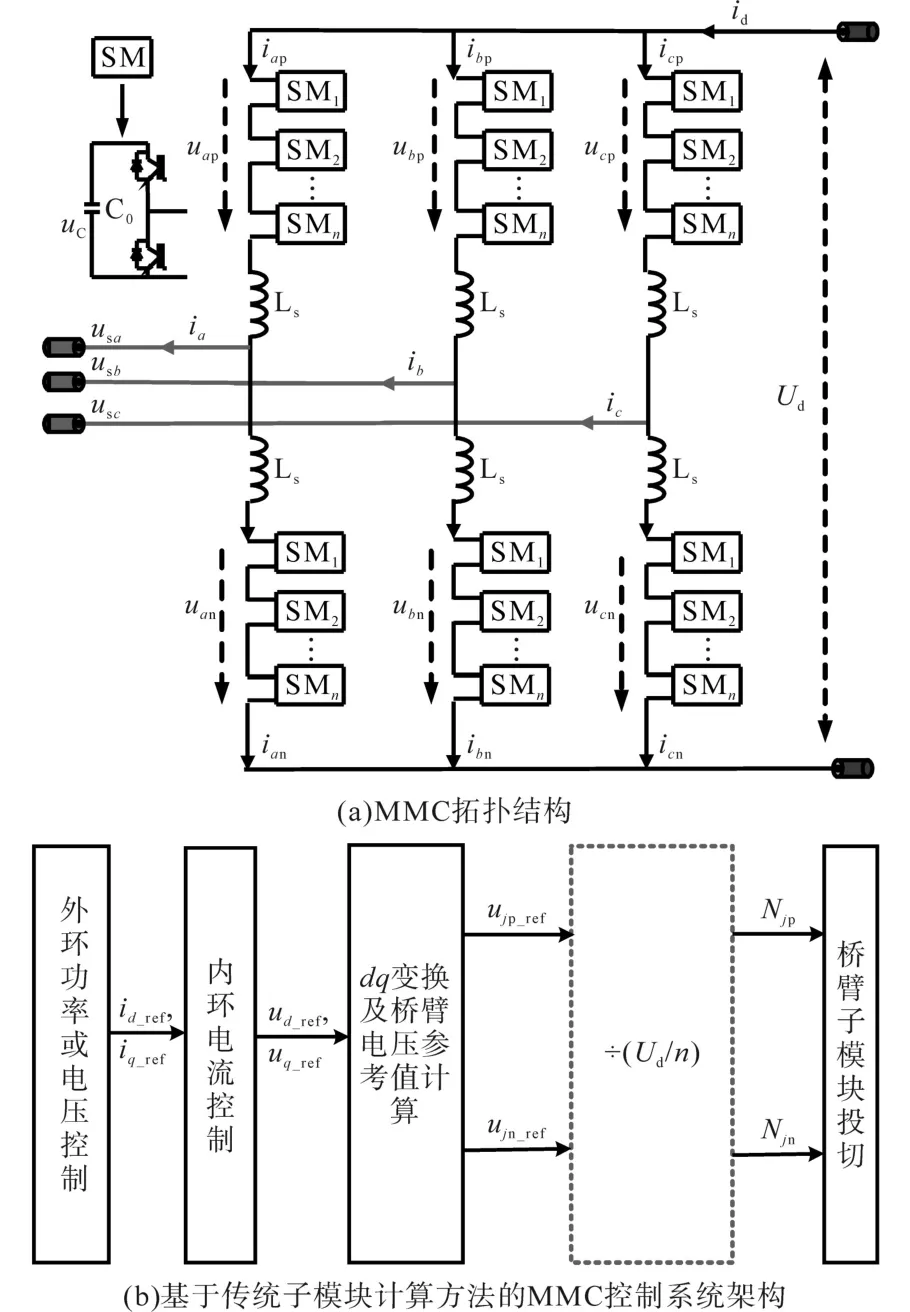
图1 MMC拓扑结构与传统子模块计算方法下的控制系统总体架构Fig.1 The topology and control system architecture of MMC based on the traditional calculation method of inserted SMs

图1a中，usj（j=a～c，表示a，b，c三相）为电网电压；ij为电网电流；Ls为桥臂电感值；SM为桥臂子模块；iap，ibp和icp为三相上桥臂电流；ian，ibn和icn为三相下桥臂电流；uap，ubp和ucp为三相上桥臂的桥臂电压；uan，ubn和ucn为三相下桥臂的桥臂电压；Ud与id为直流电压与电流；n为每个桥臂的子模块数。

基于上述参数，MMC的桥臂电流与直流电压以及桥臂电压的关系可以表示为

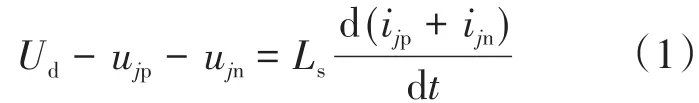
同时由文献[19-21]可知，MMC的桥臂电流可以表示如下：

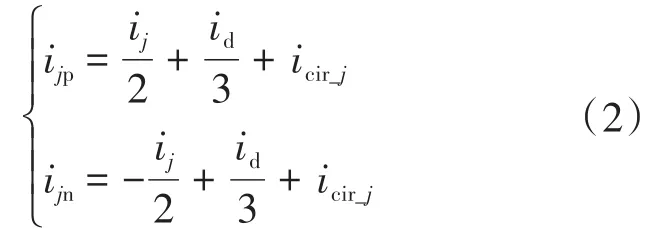
式中：icir_j为MMC桥臂环流的交流分量，主要指二倍频分量。

将式（2）代入式（1），同时忽略直流电流中的谐波分量，可得：

基于式（3）可知，当MMC应用的外部条件确定后，桥臂环流的交流分量大小主要决定于桥臂电压的变化，也就是桥臂子模块数的投切规律。

如图1b所示，在传统的子模块计算方法中，认为桥臂中子模块的电容电压处于理想状态，即：

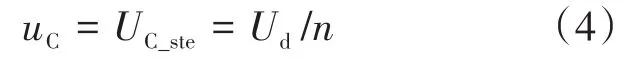
式中：UC_ste为忽略电容电压波动下各子模块的稳态电容电压值。

在图1b中，Njp与Njn分别为第j相上、下桥臂中应该投入的子模块数。

然而，由于实际运行中子模块电容存在充放电过程，因此子模块电容电压将存在一定的波动。这样，基于式（4）的电容电压值所计算的投入子模块数将与系统所期望的子模块数有所差异，从而产生桥臂环流的交流分量，并通过桥臂电感来补偿该部分电压。也就是说，传统子模块计算方法下桥臂环流交流分量的产生与投切子模块计算值的不准确密切相关。文献[20-21]基于上述原因，对于最大电平逼近调制的MMC提出了投入子模块补偿法。但该方法只能适用于最大电平逼近调制，而不能适用于载波移相调制，且应用时需要增加额外的测量设备、增加控制系统的成本。进一步地，该方法并未揭示投切子模块计算值的不准确根本原因是所采用的电容电压值计算不准确。鉴于此，本文在下节对MMC各桥臂子模块的电容电压进行了精确的计算，并据此提出了一种新的子模块计算方法以改善MMC的桥臂环流性能。

2 基于子模块电容电压精确计算的桥臂环流抑制方法

2.1 桥臂电流不含环流交流分量运行状态下的子模块电容电压精确计算

根据式（2）可知，MMC的桥臂电流中包含了基频交流分量与环流分量。其中基频交流分量与环流中的直流分量是MMC进行交直流功率交换所必须的载体。也就是说，当传输功率与运行的交、直流电压一定时，MMC桥臂电流中的基频交流分量与环流中的直流分量的大小将不可改变，是桥臂电流中的不可控分量。于此同时，环流中的交流分量则是由控制方法的不同所带来的，因此通过控制方法的改变便可以将其消除。鉴于此，为了消除MMC桥臂环流中的交流分量，现对MMC在桥臂电流中只包含环流直流分量的运行状态下的子模块电容电压进行精确的计算。

基于式（2）可知，当环流中只含有直流分量时，a～c三相的上、下桥臂电流分别为

由于a，b，c三相桥臂电流与运行的相似性，现以a相上、下桥臂中的子模块电容电压计算为例进行分析。

假设a相交流端口的电压与电流分别为

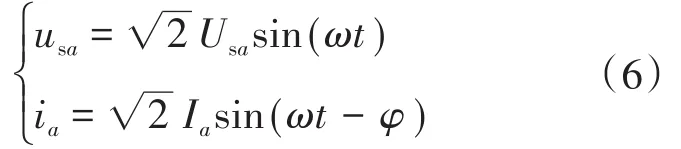
式中：usa，Usa分别为a相交流端口电压的瞬时值与有效值；ia，Ia分别为a相交流端口电流的瞬时值与有效值；ω，φ分别为a相交流端口电流的工频角频率与相位角。

根据图1a可知a相上、下桥臂的具体电压、电流关系分别为

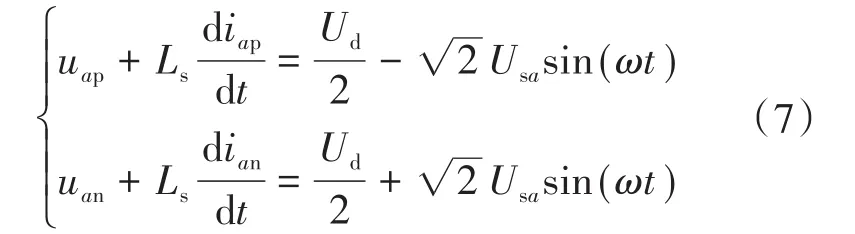
同时，将式（6）代入式（5）可得a相上、下桥臂的具体电流分别为

由于a相上、下桥臂的瞬时功率可以表示为

因此，a相上、下桥臂中所有子模块的电容电压产生的瞬时功率可以表示为

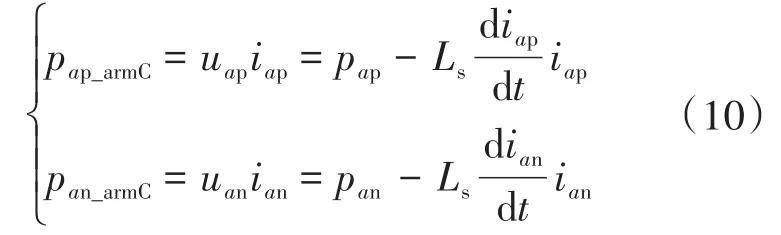
同时，考虑到瞬时功率与瞬时能量的关系，a相上、下桥臂中所有子模块电容所具有的瞬时能量为

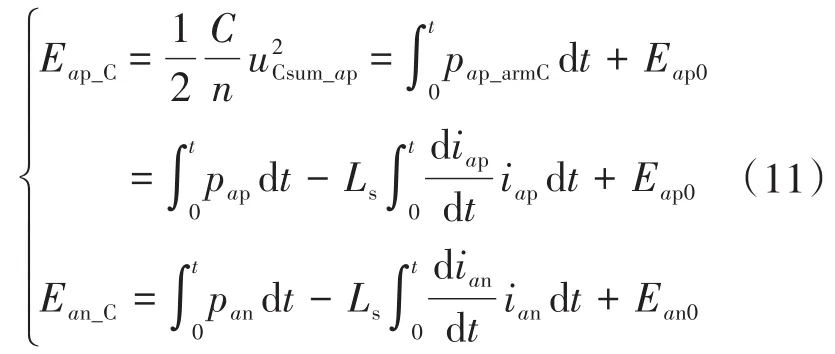
式中：Eap_C，Ean_C分别为a相上、下桥臂所有子模块电容所具有的瞬时能量；Eap0，Ean0分别为a相上、下桥臂所有子模块电容所具有的初始能量；uCsum_ap，uCsum_an分别为a相上、下桥臂所有子模块电容的电压之和；C为MMC每个桥臂中各子模块电容的平均值。

以a相上桥臂为例，将式（7）～式（9）代入式（11），可以得到桥臂电容能量的具体表达式为

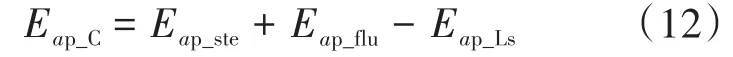
式中：Eap_ste为一个常数，其物理意义为a相上桥臂电容能量的平均值；Eap_flu为一个平均值为0的波动量，其物理意义为a相上桥臂电容能量的瞬时值的波动量；Eap_Ls也为一个平均值为0的波动量，其物理意义为a相上桥臂桥臂电感能量的变化量。

Eap_ste，Eap_flu以及Eap_Ls可以分别计算如下式所示：

基于式（11）～式（13）可知，a相上桥臂中每个子模块电容电压的瞬时值（假设均压算法效果足够好，忽略子模块电容电压之间的差异）可以表示为

相似的，其余桥臂中的子模块电容电压瞬时值也可以被求得。由式（12）～式（14）可知，子模块电容电压瞬时值只与交、直流电压、电流大小、频率以及相位有关，因此无需增加额外的测量量，便可以求得具体的子模块电容电压瞬时值。同时，当参数及运行环境一定时，桥臂电容能量的平均值Eap_ste并不会影响电容电压的瞬时值变化规律，因此通常将该值设为与直流电压有关的常数，即

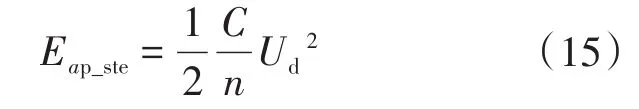
也就是，桥臂所有子模块电容所具有的初始能量Eap0为

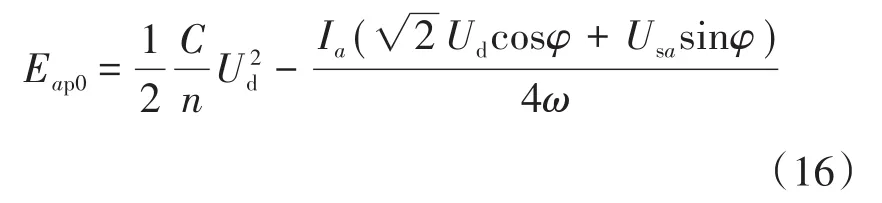
在上述设定下，子模块电容电压可以表示为下式：

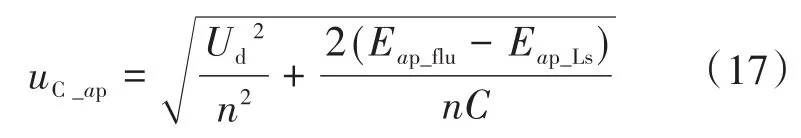
根据式（17）可知，传统子模块计算方法下的子模块电容电压忽略了子模块电容电压瞬时值的波动，而仅以平均稳态值为基准进行计算，因此必然导致桥臂中电容电压与期待的电容电压的差异，在桥臂中产生环流的交流分量，并借助于桥臂电感上的压降补偿该部分差异。

2.2 基于子模块电容电压精确计算的桥臂环流抑制方法

依据式（17），我们可以得到基于子模块电容电压精确计算的MMC桥臂环流抑制控制方法具体实现如图2所示。从图2实现流程中可知，所提环流抑制方法不需要增加任何额外的测量与控制器，只是需要利用已有的测量信息计算子模块电容电压的瞬时值后，重新计算投入子模块数即可。由于在此过程中对子模块的电容电压进行了精确地计算，各时刻桥臂电容的实际电压与期待电压几乎一致，从而使环流中的交流分量得到了良好地抑制。

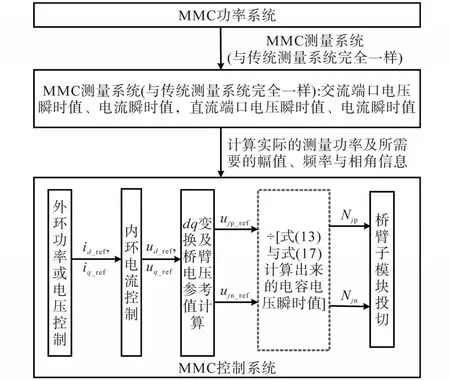
图2 基于子模块电容电压精确计算的桥臂环流抑制控制实现框图Fig.2 The diagram of the proposed arm circulating current suppression method based on the accurate calculation of SM capacitor voltage

3 仿真验证

为了对所提的环流抑制策略进行验证与分析，在Matlab/Simulink仿真平台中搭建了一个±10 kV/20 Mvar的MMC换流器模型，具体参数为：额定交流电压10 kV；额定直流电压±10 kV；额定容量20 Mvar；桥臂电感3.2 mH；直流电压基准值20 kV；交流电压基准值10 kV；桥臂电容电压基准值0.5 kV；桥臂电抗电压基准值1 kV；桥臂子模块数40个；桥臂子模块电容30 mF；运行方式定直流电压；负载电阻20 Ω，25 Ω；直流电流基准值1 kA；交流电流基准值1 kA；桥臂环流基准值1 kA。

图3为不同子模块计算方法下MMC的主要电气量仿真结果。由图3a可知，无论是传统子模块计算方法，还是本文所提的基于电容电压精确计算的子模块方法均能实现直流电压的精确控制；同时，根据图3a与图3b可知，二者在交、直流端口的特性基本一致。然而，由于内部子模块计算方法的不同，图3c中二者的子模块电容电压瞬时值、桥臂电流瞬时值以及桥臂电感电压瞬时值均不同。在3 s之前，MMC的子模块计算方法为传统的基于电容电压稳态平均值方法，由于投入子模块的实际值与系统期望值有所差异，在桥臂电流中产生了较大的二次谐波分量，同时该分量在桥臂电感上产生了谐波电压，桥臂电感电压不再为正弦波；进一步地，环流中的二次谐波分量也增加了电容电压的波动。对比之下，在3 s之后，采用本文所提的子模块计算方法，环流中的交流分量明显减小，桥臂电感电压也恢复了正弦波形，进而也减小了电容电压的波动。图3a～图3c说明了本文所提子模块计算方法在桥臂环流抑制方面的可行性与有效性。

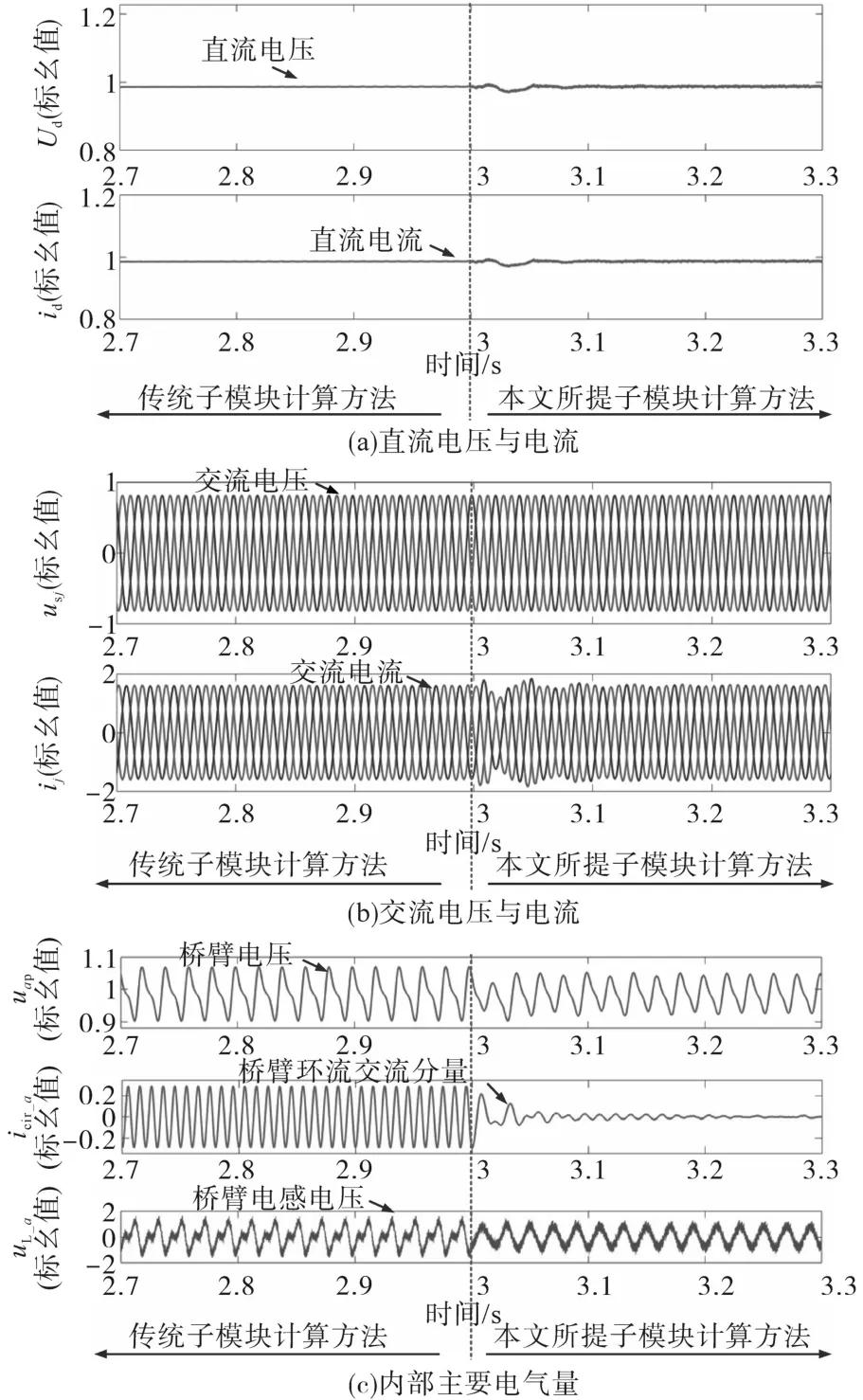
图3 不同子模块计算方法下的MMC运行对比Fig.3 The operating characteristics comparison for MMC under the different calculation methods of inserted SMs

图4为不同子模块计算方法下MMC的子模块投入状态对比。从图4中可知，由于对子模块电容电压的估计值不同，本文所提方法与传统方法计算后的投入子模块明显不同，这是本文所提方法能够抑制桥臂环流交流分量的根本原因。同时，无论是最大电平逼近调制，还是载波移相调制，本文所提的方法均适用，具有良好的通用性。

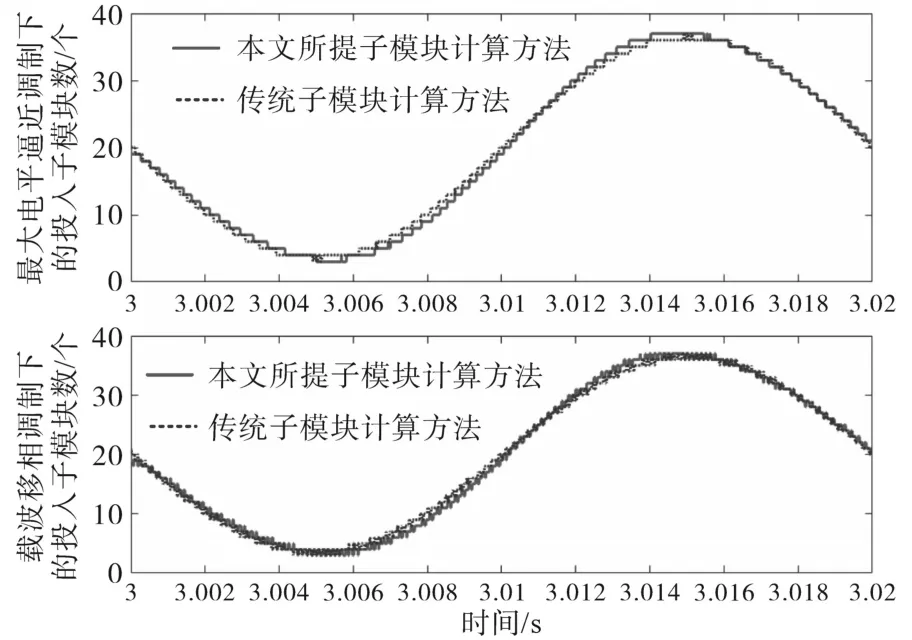
图4 不同子模块计算方法下的MMC子模块投入情况对比Fig.4 The comparison of MMC SMs input under the different SMs calculation methods

图5为直流电压阶跃以及传输功率阶跃下所提子模块计算方法在MMC中的应用仿真结果。其中，5 s前，MMC控制直流电压为20 kV，负载电阻为20 Ω；5～6 s，MMC控制直流电压阶跃为18 kV，负载电阻保持为20 Ω不变；6 s后，MMC控制直流电压保持为18 kV不变，负载电阻变为25 Ω。从仿真结果可知，当直流电压发生阶跃时，由于负载电阻并没有发生变化，此时MMC的传输功率以及交、直流电流值将发生变化，且桥臂环流的交流分量经过短暂的波动后也恢复了稳定状态；进一步地，功率阶跃时，桥臂环流的交流分量同样出现了相似的情况，不再赘述。