电流控制交错Boost变换器精确建模与设计

阎昌国 ，龚仁喜，安玉，李青，刘小雍

（1.遵义师范学院工学院，贵州 遵义 563006；2.广西大学电气工程学院，广西 南宁 530004）

近年来，开关电源高频化、高功率化的快速发展，对其寄生参数的利用也提出了一些新的要求[1]。交错Boost变换器作为中大功率开关电源的前级电路，在提高功率因数、改善电网供电质量方面发挥着至关重要的作用[2-3]。建模时，考虑寄生参数，对交错Boost变换器的设计与应用十分重要，它不仅能建立更为精确的数学模型去描述电路实际工作状况，还能缩小实际电路与传统理想模型之间的偏差。迄今为止，对交错Boost变换器的建模研究已经有了一些成果。文献[4]用状态空间平均法获得了占空比D＞0.5与0＜D＜0.5两种情况下的数学模型，但缺乏对控制级进行建模，所获模型为不完整的理想模型。文献[5]运用时间平均等效原理，虽建立了包含功率级与控制级在内的交流完整小信号模型，但没有考虑元器件寄生电阻等非理想因素，仍属于理想模型。文献[6]基于非线性动力学理论，虽考虑了部分元件的寄生电阻，但所建模型为离散迭代映射模型，不便于直接指导实际电路的设计。鉴于此，本文在上述文献的基础上，提出了一种基于峰值电流控制的非理想交错Boost变换器设计方案。该方案考虑了各元器件寄生电阻、二极管寄生电压、电感电流纹波等非理想因素的影响。文中运用时间平均等效原理，获得了峰值电流控制连续导电模式（continuous conduction mode，CCM）下非理想交错Boost变换器完整的交流小信号模型，通过将该模型与传统理想模型对比分析，证实了所建模型较之传统理想模型更为精确。同时，所提方案的正确性与可行性也通过了实验的验证。

1 系统方案

图1为本文提出的一种峰值电流控制非理想交错Boost变换器系统设计方案，它由主电路功率级、电压控制器与峰值电流控制器三部分构成。主电路为非理想交错Boost变换器，由带寄生电阻 RL1，RL2的非理想电感 L1，L2，带寄生电阻RS1，RS2的功率开关管S1，S2，带寄生电阻RF1，RF2与寄生电压UF1，UF2的二极管D1，D2及带寄生电阻RC的电容C组成。图1中，Gv（s）为电压控制器补偿网络，clk1与clk2为周期等于开关管工作周期T（其频率用f表示）、相位相差180°的时钟脉冲信号，目的是使两个RS触发器的置位输出相差半个周期，实现交错控制。

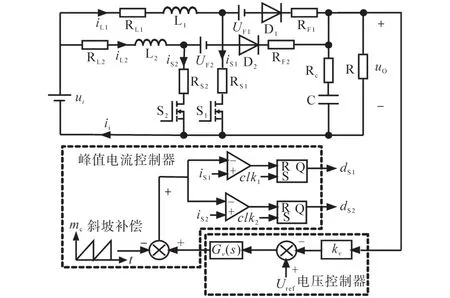
图1 系统方案Fig.1 System plan

2 建模

2.1 功率级建模

为简化分析，假定电感L1=L2=L，寄生电阻RL1=RL2=RL，RS1=RS2=RS，RF1=RF2=RF，瞬时占空比dS1=dS2=d。由于主电路交错Boost变换器在结构上可以看成是由两个基本Boost并联构成，因此，在电感电流纹波的影响下，按照文献[7]，可将CCM下交错Boost变换器各非理想参数折算到各自对应的电感支路。同时，根据时间平均等效原理[8]，用受控电流源diL替换开关管S1与S2，用受控电压源duo替换二极管D1与D2。于是，得到了如图2所示的等效电路。

图2 等效的主电路Fig.2 Equivalent main circuit

图2中，UE为UF折算后的等效电压，RE为除Rc外的各寄生电阻折算后的等效电阻，其折算关系式分别为

式中：r为电感电流纹波率[9]；ΔiL为电感电流纹波；IL为电感电流直流分量；D为占空比d的稳态值。

对图2引入交流小信号扰动[10]，即令瞬时值：分别为对应直流分量D，Ui，Uo，IL的交流扰动分量，经分离扰动，忽略直流分量、交流二次分量与后，得到如图 3 所示的交流小信号等效电路。

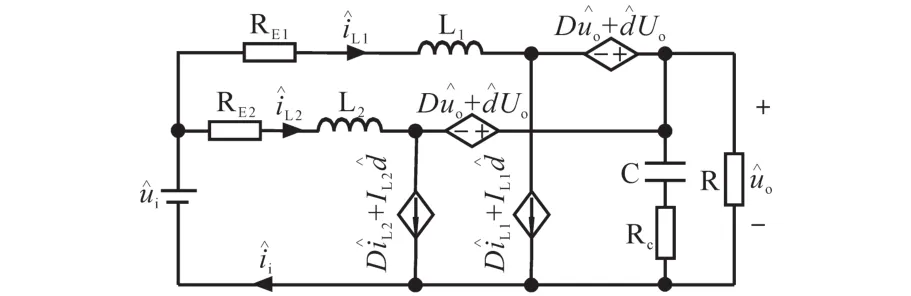
图3 交流小信号等效电路Fig.3 AC small signal equivalent circuit

对图3进行拉普拉斯变换，可得

由式（4）可得：

式中：G1（s）为输出电压对输入电压的传递函数；G2（s）为电感电流对输入电压的传递函数；G3（s）为输出电压对占空比的传递函数；G4（s）为电感电流对占空比的传递函数。

联立式（5）～式（8）可得系统主电路功率级s域的数学模型为

2.2 峰值电流控制级建模

图4为峰值电流控制的电感电流波形，m1为电感电流上升斜率，m2为下降斜率，m3为斜坡补偿斜率。由文献[11]可得电感电流在一个开关周期的平均值：

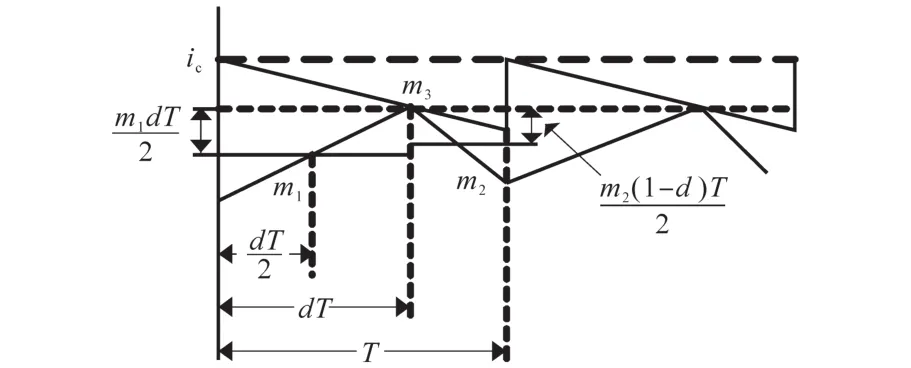
图4 峰值电流控制的电感电流波形Fig.4 Inductance current waveform of peak current control

在CCM下，对非理想交错Boost变换器有

对式（10）～式（12）进行小信号扰动分离得：

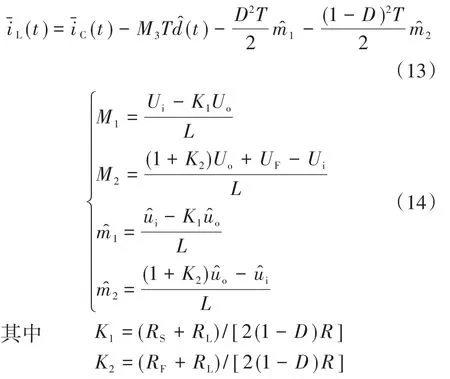
将式（14）代入式（13），即可得到峰值电流控制级s域的数学模型为

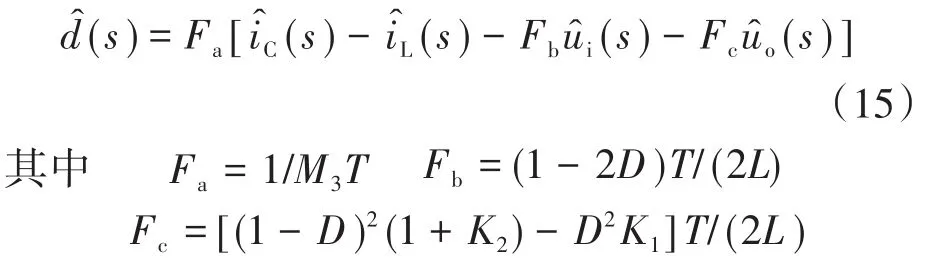
结合图1，在式（9）、式（15）的基础上，即可得到系统完整的交流小信号模型如图5所示。

图5 完整的交流小信号模型Fig.5 Complete AC small signal model

3 模型分析与设计

3.1 模型分析

基于上述理论，作出了传递函数G3（s）在四种工作状况下的Bode图如图6所示。各工况条件如下：1）RE=0.75 Ω，Rc=0.1 Ω，表示考虑了各元器件寄生电阻、二极管寄生电压、电感电流纹波等非理想因素，即是本文所建立的非理想模型；2）RE=0 Ω，Rc=0.1 Ω，表示仅考虑电容的寄生电阻；3）RE=0 Ω，Rc=0 Ω，表示不考虑任何非理想因素，即传统理想模型；4）RE=0.75 Ω，Rc=0 Ω，表示仅不考虑电容的寄生电阻。

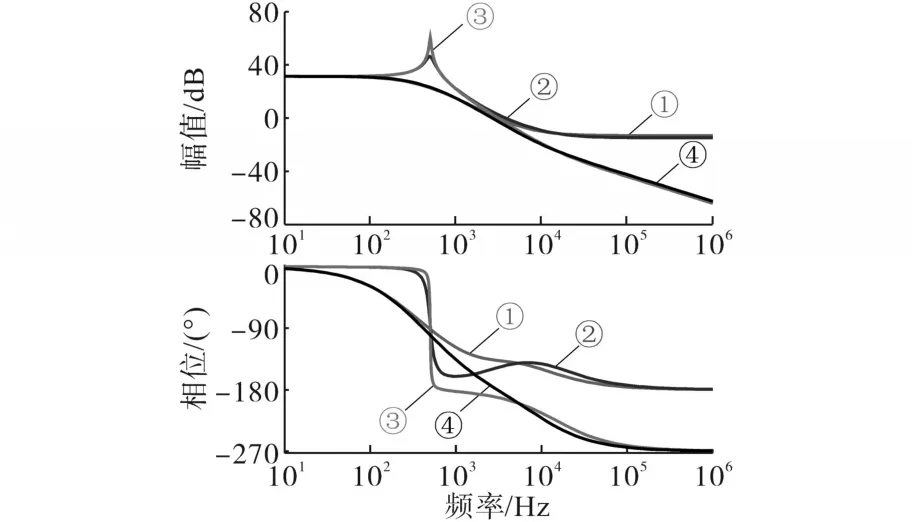
图6 G3（s）的Bode图Fig.6Bode diagram of G3（s）

由图6可以看出：对比工况①与工况③可知，两种模型在转折频率处有较大的差异，该差异主要表现为谐振峰值的大小不同；对比工况②与工况③、工况③与工况④可知，增大Rc对变换器的高频特性有影响，而对谐振峰值的改善并不明显；而当增大RE时，该谐振峰值会大大减小，相角变化也会变缓，说明该差异是由变换器的寄生参数所引起的，从而证实了本文所建立的模型较之传统理想模型更为准确，更能反映电路的实际工作情况。

3.2 环路设计

式中：ki为电流采样系数。

根据文献[12]，采用等效分析法，将峰值电流控制级用等效功率级代替，新的功率级与电压控制级组成了如图7所示的等效单环控制系统。则可得等效后的开环传递函数To(s)为

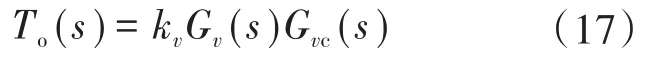
图7 等效单环控制系统Fig.7 Equivalent single loop control system

由文献[13]可知，补偿前，To(s)存在穿越频率过低、相位裕量较大的缺点。为提高系统响应速度与动态性能，选用了单零点双极点型控制器Gv(s)来进行补偿。根据文献[14]的补偿方法，选取ki=0.025，kv=0.125，得到补偿结果如图8所示。

图8 To（s）的Bode图Fig.8Bode diagram of To（s）

由图8可以看出，补偿前，系统穿越频率约为259 Hz，相位裕量约为102°；补偿后，系统穿越频率约为6 kHz，相位裕度约为60°，增益裕量约为10 dB，满足稳定设计要求。

4 实验结果

峰值电流控制的非理想交错Boost变换器实验参数如下：ui=10.8V，uo=20V，R=20Ω，L=125μH，RL=0.67 Ω，C=470 μF，Rc=0.1 Ω，RS=0.055 Ω，RF=0.025 Ω，UF=0.4 V，f=50 kHz，r=0.4，m3=0.75m2，实测波形如图9所示。

图9 实验波形Fig.9 Experimental waveforms

图 9a为开关管 S1，S2的驱动波形Ugs1，Ugs2，由图9可知，一个周期内，开关管是在S1通S2通、S1通 S2断与S1通 S2通、S1断 S2通之间重复切换，这与文献[6]中D＞0.5时的工作状态分析一致，说明系统能正确实现交错控制。图9b为系统起机时的输出电压波形Uo，由图可知，系统输出延迟时间短，约为5 ms，输出无明显震荡现象，超调小，超调量约为5.8%。说明基于上述理论分析与环路设计，系统具有良好的稳态性能。图9c为带50 Hz、0～1 A动态负载下的输出电压测试波形，由图可知，输出电压Uo在负载电流Io切换瞬间能快速响应，且无过冲现象，波动峰峰值约为0.54 V。说明基于上述理论分析与环路设计，系统具有动态响应快，输出电压波动小的优点。

5 结论

基于对实际电路准确建模的需求，在考虑各元器件寄生电阻、二极管寄生电压、电感电流纹波等非理想因素的影响下，本文提出了一种峰值电流控制的非理想交错Boost变换器系统设计方案。通过对系统功率级与控制级的精确建模，得到了CCM下系统完整的交流小信号模型，模型直观明确，更能准确反映实际电路的工作情况。同时，基于该模型，完成了控制环路设计，并通过实验证实了该方案的正确性与可行性。