周期荷载作用下钢轨缺陷检测分析

孙国营，刘志明，冯推银，于尧，李佳霖

(1. 北京全路通信信号研究设计院集团有限公司，北京 100070；2. 中南大学交通运输工程学院轨道交通安全教育部重点实验室，湖南长沙 410075)

我国经济快速，高质量的发展，推动着铁路行业的蓬勃发展。伴随着轨道列车速度的不断突破和路网逐步密集，运输能力在不断提高，这也对铁道线路服役状态有了更高的要求。钢轨是整个铁道线路的重要组成部分，钢轨服役过程中，导致钢轨产生断裂缺陷的主要因素有重载荷反复冲击、轮轨滚动接触疲劳裂纹、压溃、腐蚀以及钢轨内部缺陷、材料退化。钢轨断裂可能导致线路中断或列车脱轨、倾覆等重大事故，进而造成重大的人员伤亡和财产损失[1]。钢轨的服役状态直接影响铁路的运输安全，因此能够及时准确地检测出钢轨件等部件的缺陷，对运输行业安全高质量发展具有重大的意义。目前，铁路钢轨检测通常是通过搜集与分析轨道检测车辆所得到的响应信号来判断轨道的缺陷，其评价结果易受车辆本身振动等环境影响。此外，铁路钢轨检测技术还有超声波检测、电磁检测、视觉检测等，都具有检测周期较长，数据分析量大等缺点。如何充分地利用钢轨实际的信号数据来快速高质量的反馈钢轨当前服役状态信息，提高钢轨断裂等缺陷的检测速度，为线路故障早期预警提供基础数据来源成为亟待解决的关键问题。SADEGHI 等[2-3]提出了通过轨道几何状态判断轨道病害的评价指标与方法，对轨道几何状态的评价采用的是单点检测基础数据，各个指标之间保持相互独立。卢超等[4]分析了超声相控阵技术在钢轨缺陷检测中的应用。胡松涛等[5]研究了电磁超声表面波技术在不同深度钢轨裂纹上的散射特性及反射波信号响应特点，能够有效检测钢轨踏面上的裂纹。许鹏等[6]提出一种利用增强磁场涡流抑制趋肤效应的方法来检测钢轨缺陷，结果表明钢轨缺陷在50 V 直流激励条件下信号特征更容易区分。KANG 等[7]利用漏磁技术分析了钢轨的局部断裂等故障检测。WALLE等[8]利用感应热成像技术研究钢板缺陷，为该技术在钢轨断裂检测上的应用奠定了基础。王海涛等[9]研究了计算机视觉检测技术在钢轨缺陷中的应用，并分析了钢轨断裂程度信息。田铭兴等[10]研究光纤、应力、声波实时监测断轨的方法，分析了不同断轨检测方法的优缺点。石敏莲等[11]基于振动数据研究了轨道结构的缺陷，同时指出了钢轨的振动响应对轨道缺陷状态较为敏感。胥帅[12]基于车辆受振动产生的加速度等数据，在时域和频域对比了正常轨道与存在病害轨道的车辆振动响应的区别来对轨道下结构的故障状态进行判断。宋纾崎[13]研究指出，对于钢轨而言，其振动加速度会沿着钢轨纵向传播，可以影响到前后10个轨枕的距离，尤其是在前后3 个轨枕间距内影响较大。向玉玲[14]通过实验验证了振动信号在钢轨上传播的可能性，并指出了振动波通过接头轨缝时只发生了很小的衰减，振动波形保持完好。基于上述研究发现，根据钢轨振动数据检测其断裂缺陷具有可行性，但相关研究还比较少。因此，对钢轨断裂等不同缺陷条件下的振动响应数据获取还需开展更多的研究工作。本文以高速铁路中最常见的CRTSIII型板式无砟轨道为研究对象，基于ANSYS 等仿真软件平台，建立起了无砟轨道的有限元模型，在钢轨上设置2 个检测节点，检测点1 坐标为：(5 000,0, 0)，检测点2 坐标为：(25 000, 0, 0)，通过对钢轨一端施加节点周期荷载激励，在多次仿真实验中提取钢轨不同程度断裂缺陷的振动规律特征。对比2个检测节点收集钢轨受迫振动产生的加速度响应信号，可得到2个检测节点之间检测区域中所存在的轨道缺陷类型。本文将接头轨缝的情况按照正常的钢轨处理，主要研究对行车安全造成直接影响的钢轨完全断裂和钢轨50%截面断裂2种类型，其余钢轨缺陷可基于此方法研究对应的振动规律特征。本文提出的检测方法属于无源检测，具有成本低廉，使用过程简便，可靠性高且不会对轨道本身造成影响等特点，能够直接收集钢轨实时信号有效地提高轨道检测的工作效率，减少线路维护的时间。

1 无砟轨道钢轨受迫振动系统分析

在对钢轨振动分析前，应分析无砟轨道的结构组成与受力情况。针对研究对象，所需数据，对实际轨道结构进行合理简化，建立起相应的动力学模型。为了研究轨道结构在各个节点或区域上的振动响应情况，本文采用ANSYS 有限元软件进行建模。

1.1 无砟轨道动力学模型

无砟轨道经过20 多年的发展，其有关技术也日渐成熟，目前板式无砟轨道的类型有CRTSI 型、CRTII 型和CRTSIII 型，如图1 所示。无砟轨道结构具有可靠性高，稳定性好，轨道结构轻，易于维护等特点，广泛应用于我国新建的高速铁路轨道[15]。板式无砟轨道的主要组成部分有：钢轨、扣件、轨道板、自密实混凝土、CA砂浆层等。

由于本文主要研究钢轨的受迫振动，受轨道基础的影响不大。选取CRTSIII型板式无砟轨道的结构，建立了相对应的动力学模型，如图2 所示。在模型中，采用的是分层建模的思想。整个轨道结构从上到下依次是：钢轨，扣件，轨道板，CA砂浆层，地基。其中扣件和CA 砂浆层采用弹簧—阻尼单元来模拟。图2(a)中给出了用于收集钢轨受振动产生的加速度响应信号的2 个检测节点，2 个检测节点之间的区域便是检测区域。

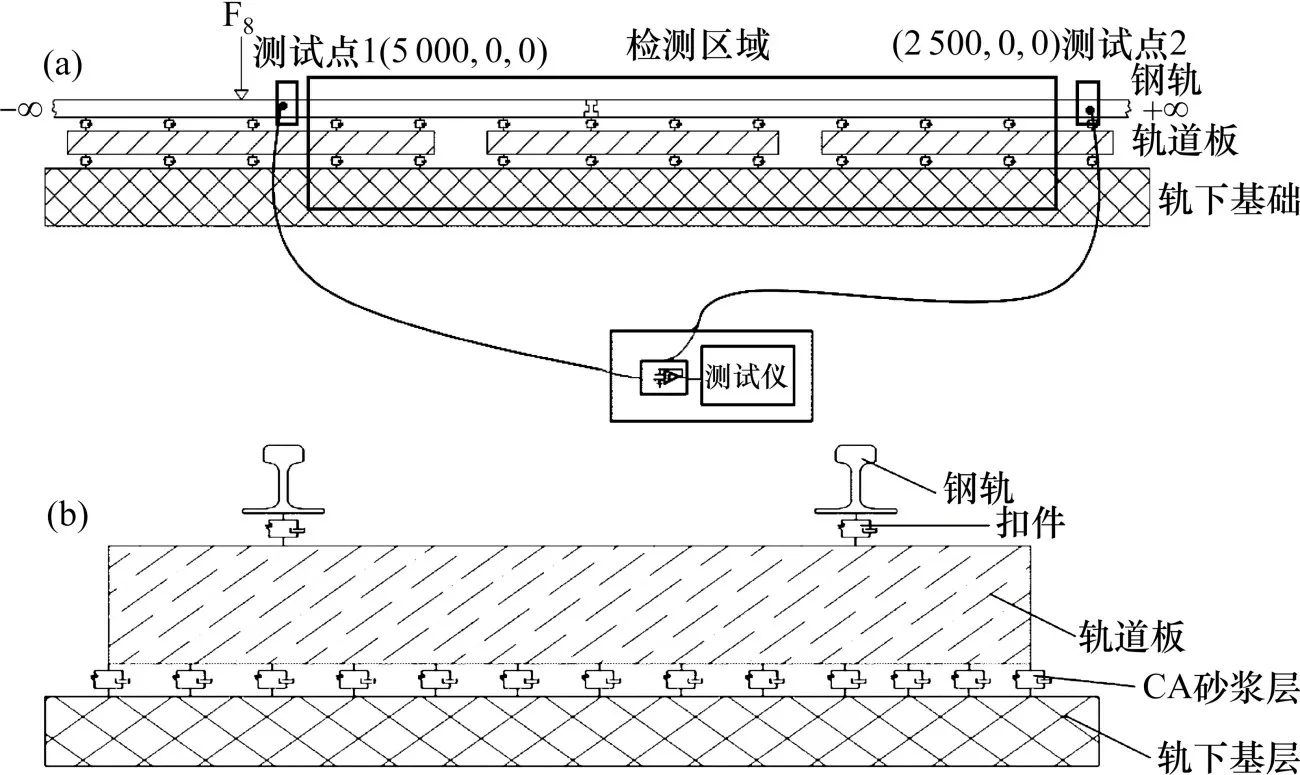
图2 CRSTIII型板式无砟轨道动力学模型Fig.2 Dynamic model of CRSTIII slab ballastless track

1.2 无砟轨道系统振动方程

本文提出的无砟轨道缺陷检测分析方法是通过研究给钢轨施加基础激励后，获取其在某节点处的加速度信号时频域特性以及提取各种缺陷对应的规律特征，能够对整个轨道结构进行监测和缺陷预警。激振力可以是轨道车辆行驶本身所带来的激励也可以是其他检测设备对钢轨所施加的力，本文研究的情况是在固定点施加节点周期载荷作为基础激励。

1) 在动力学模型中，选取钢轨质量和位移为研究对象，其整体可视为质量—弹簧系统[16]，其中钢轨采用有限元方法进行离散，可以看成是一个多质点系统，其运动方程可以用式(2)来表示：

[M]{x¨ }+[C]{x˙}+[K]{x}={F} (1)

其中：M，C，K为钢轨离散后自身质量、扣件阻尼和扣件刚度矩阵，x¨，x˙，x为钢轨的竖直加速度矢量，竖直速度矢量，竖直位移矢量，F表示外荷载。

2) 本文对钢轨离散后的振动进行分析时，只考虑垂向力的影响，并且考虑扣件的影响，将钢轨看作弹性基础上无限长的梁，根据D’Alembert原理以及钢轨垂向力平衡可得某微段钢轨的振动微分方程[11]：

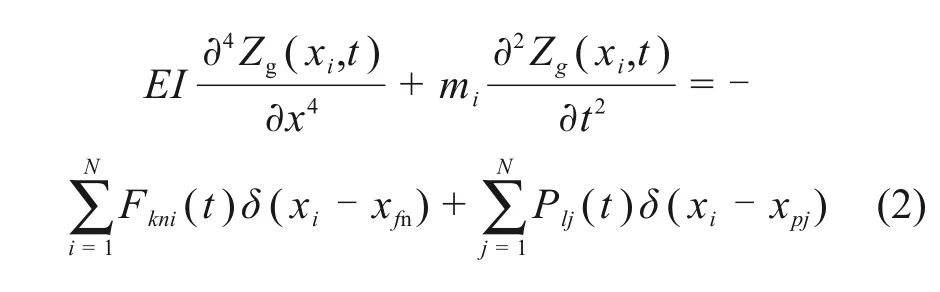
其中：E，I分别为钢轨的杨氏模量和极惯性矩；mi为单个钢轨单元的质量；Fkni(t)，Pij(t)为第n个扣件处对钢轨的垂向反力和在第j个钢轨单元上施加的激振荷载，xi，xfi，xpj分别为第i个钢轨单元出的坐标，第n个扣件处的x坐标以及施加了激振荷载的第j个钢轨单元处的x坐标，Zg(xi,t)为第i个钢轨单元在t时刻的实际振动位移。

第n个扣件处对钢轨的垂向反力Fkni(t)由式（3）计算

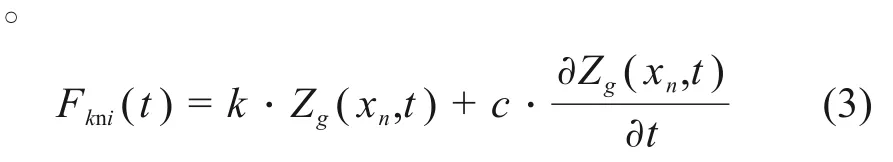
式中：k，c表示扣件的刚度系数和阻尼系数；Zg(xn,t)表示在扣件连接处钢轨的垂向振动位移。

由于本文主要研究钢轨的振动，故轨道板的振动方程此处不作讨论。本文研究的是在不同轨道缺陷下加速度信号在时频域的规律。要提取对应的规律特征，需先在时域将Zg(x,t)对时间t求二阶偏导，随后对时域得到的二阶偏微分方程进行傅里叶变化处理，便可得到在频域的加速度信号频谱图。

2 无砟轨道有限元模型

无砟轨道具有多层性和复杂性[17-19]，本文运用ANSYS 有限元分析软件建立了无砟轨道结构模型，各个组成结构的基本参数是根据CRSTIII型无砟轨道的材料参数进行定义，如表1所示。扣件由弹簧-阻尼单元模拟，垂向刚度为：K=5×107N/m，垂向阻尼为：C=7.5×104(N·s)/m，CA 砂浆层同样采用弹簧—阻尼单元模拟，垂向刚度为：K=7×107N/m，垂向阻尼为：C=3.1×104(Ng·s)/m[16]。

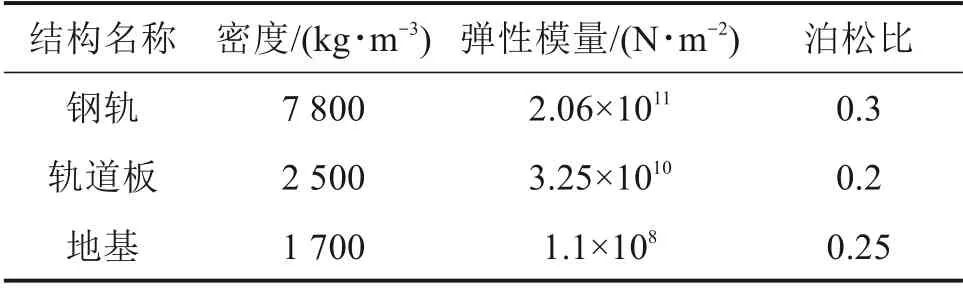
表1 无砟轨道结构参数Table 1 Structure parameters of non-ballasted track

2.1 无缺陷轨道模型

本文所建立的板式无砟轨道结构模型主要由：钢轨、扣件、轨道板、CA 砂浆层及地基等几个部分组成，轨道模型具有对称性[20]，本文对其进行了简化处理，选取单侧钢轨模型进行离散处理。首先钢轨断面选取高速铁路常用的60 号钢轨截面参数，采用的是梁单元beam188模拟；其次扣件采用线性单元来模拟，选用combin14 弹簧—阻尼单元进行模拟，在轨道振动系统分析中，主要考虑的是垂向振动，因此可忽略扣件发生弯曲和剪切的可能；最后，轨道板和地基采用的是实体单元solid45 进行模拟，轨道板和地基之间的CA 砂浆层采用的是combin14 弹簧—阻尼单元来模拟。这样既能反映轨道下结构的基本特性，又能提高计算效率。理论上钢轨可以视为有支撑点的连续无限长的弹性梁，但为了减少计算成本，本文将钢轨简化成有限长的简支梁模型，同时为了消除边界效应的影响，本文的轨道长度取50 m，并在端部进行了6个自由度的约束。所建立的板式无砟轨道振动分析模型如图3所示。本文研究的轨道缺陷类型有：钢轨截面全断裂，钢轨50%截面断裂。其他的轨道缺陷或者组合缺陷可通过类似的方法进行分析。对于钢轨截面全断裂工况而言，钢轨断开缝隙为：1 mm，可通过删除其中一个钢轨单元来模拟；对于钢轨截面50%断裂工况而言，取其中1 mm长的钢轨单元作偏心处理来模拟。

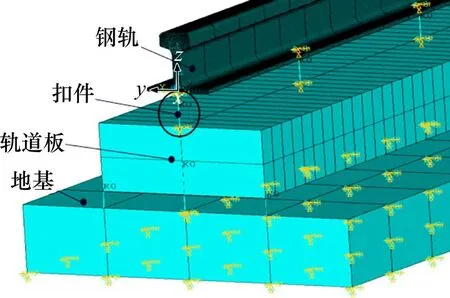
图3 板式无砟轨道仿真模型Fig.3 ANSYS simulation model of non-ballasted track

3 钢轨振动时频域特性分析

为了分析和提取不同轨道缺陷情况下的加速度信号在时频域的规律特征，本文首先研究的是无缺陷轨道的振动特征。通过对比分析无缺陷轨道和存在缺陷轨道同一检测点的振动响应值，便可判断出轨道缺陷的区域以及缺陷类型。考虑到垂向轮轨作用力峰值一般大于轴重，为了不对钢轨造成二次破坏，在钢轨上的节点载荷的峰值取等值轴重所产生的压力。动车组轴重一般小于17 t，本文以单根钢轨为研究对象，故本节分析了在峰值为85 kN 的节点周期激振力作用下，钢轨在检测点处的加速度时域曲线以及对应的频谱，并给出了不同缺陷状态的钢轨对应的特性。遵守控制变量原则，2 个检测点应安装在不同钢轨截面的轨腰或轨底中同一位置。根据振动波在钢轨上的传播特性[5]，一般情况下振动波能在钢轨中传播的距离可达200 m 以上，2 个检测点之间的距离在振动波可传播的范围内即可，考虑到本文所建模型长度为50 m，故2个检测点之间的距离设定为20 m。

3.1 无缺陷轨道的振动特性分析

下面将通过对无缺陷钢轨的振动加速度以及振动加速度频谱的分析来研究钢轨在周期荷载作用下的振动特性。为了更方便提取规律特征，取节点周期荷载作用2个周期后的振动响应数据进行分析。

1) 加速度时域分析

通过仿真计算得到钢轨振动加速度时域曲线，如图4所示。

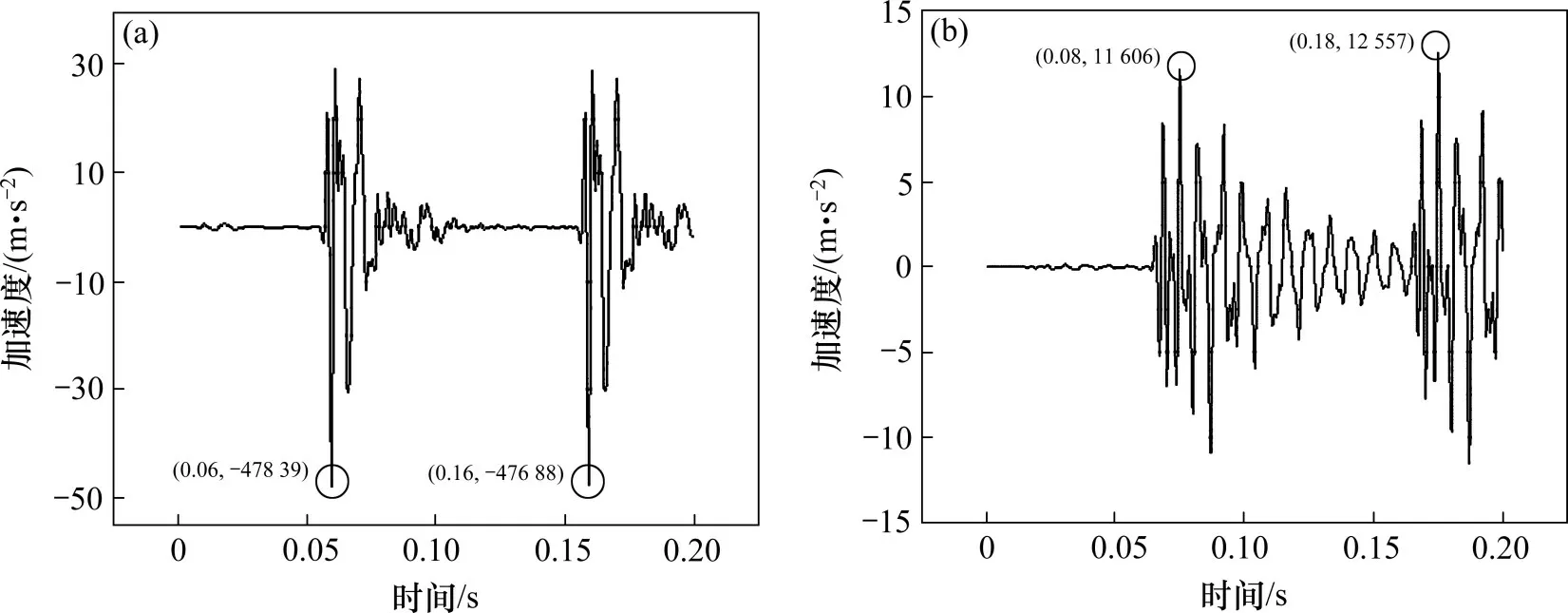
图4 无缺陷轨道检测点处振动加速度时域曲线Fig.4 Time-domain curves of vibration acceleration at the detection point of normal track

图4 中，在周期荷载的激振作用下，2 个检测点的钢轨振动加速度响应是成周期性的，均是随着激振力的增大而增大，在激振力一个周期结束后振动逐渐衰减，最后趋近于平衡状态。本文选取其中2个周期的钢轨振动加速度进行分析，振动加速度的峰值取2 个周期内最大值：检测点1 在0.06 s时，振动加速度峰值为47 839.4 mm/s2；由于检测点2的位置在后，周期激振力产生的振动波延后达到，故加速度峰值的时间有所延后，检测点2在0.08 s时，振动加速度峰值为11 578.7 mm/s2。

2) 加速度频谱分析

将钢轨上2个检测点处收集到的振动加速度数据通过傅里叶变换得到对应的振动加速度频谱，如图5 所示。本文根据信号处理概念对频域的研究，采用幅值平均值、幅值最大值、振动频率3个指标进行分析。

从图5中可以看出，由于周期荷载的激振，钢轨振动加速度在频域出现多个峰值。本文主要研究频谱图中的幅值平均值和幅值最大值来分析振动特征。在检测点1处：1)整体来看，幅值的平均值为：377.3 mm/s2。2) 在频率为120 Hz 时，钢轨加速度幅值达到最大为3 347.3 mm/s2。在检测点2处：1) 幅值的平均值为：125.4 mm/s2。2) 在频率为120 Hz 时幅值达到最大为2 026.4 mm/s2。这是由于在以上2 个频率时，2 个检测点处的钢轨发生了共振，此时钢轨的加速度幅值达到最大。同时由钢轨在2 个检测点的振动加速度频谱图5 可知，振动能量在0～1 000 Hz 频段均有分布，主要分布在50～700 Hz频段。

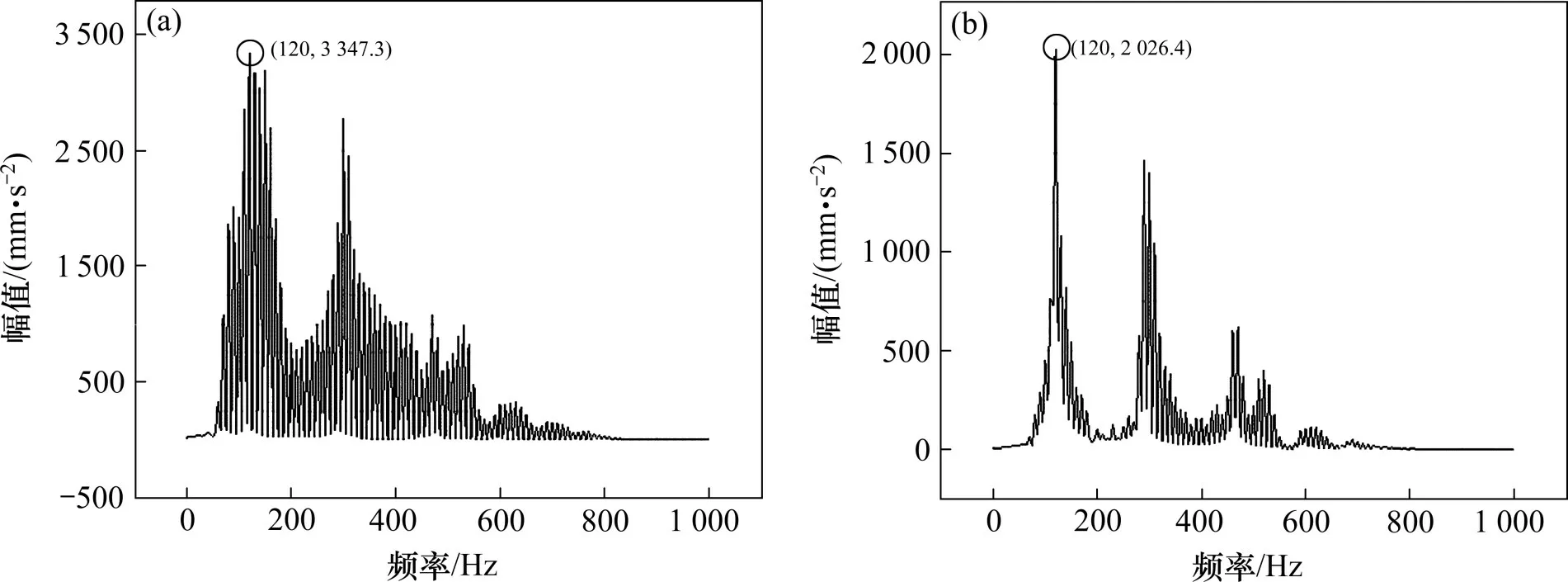
图5 正常轨道检测点处振动加速度频谱图Fig.5 Vibration acceleration frequency spectrum at the detection point of normal track

3.2 缺陷轨道振动特性分析

3.2.1 钢轨50%截面断裂

1) 加速度时域分析在钢轨缺陷中，存在不同程度的裂缝和不同程度的截面断裂的情况。在本文中主要研究的缺陷为钢轨截面50%断裂，其他缺陷可以采取相同的方法进行分析。钢轨截面50%断裂时，钢轨的振动加速度时域曲线如图6所示。

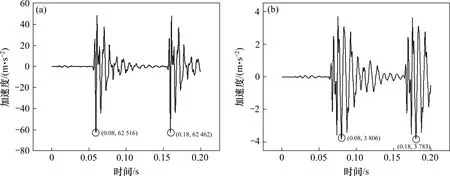
图6 钢轨50%断裂检测点处振动加速度时域曲线Fig.6 Time-domain curve of vibration acceleration at the detection point of the rail semi-fracture

从图6中可以看出，在钢轨截面存在50%断裂的情况下，钢轨在2个检测点处的振动加速度也呈现出周期性。但在检测点1 处，振动加速度于0.06 s时达到最大值为62 516.3 mm/s2，比无缺陷轨道同一时期的最大峰值高30.7%。此外，在其余时刻同时期对比，振动加速度响应值都有所增加；在检测点2 处，振动加速度处于0.08 s 时达到最大值为3 806.7 mm/s2，比无缺陷轨道同一时期的最大峰值下降了67.1%，此外，在各个时刻与无缺陷轨道检测点2处同比，振动加速度的响应值均有所下降。

2) 加速度频谱分析轨道缺陷为钢轨50%截面断裂时，2 个检测点处振动加速度频谱图如图7所示。

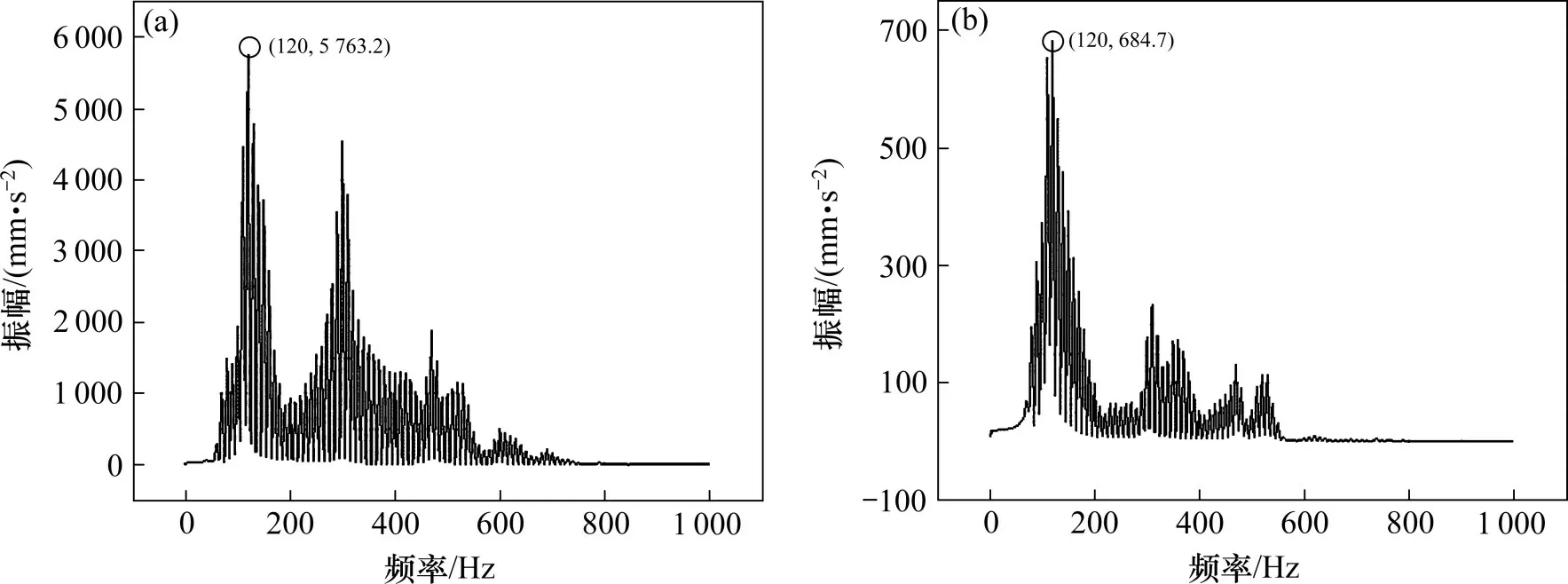
图7 钢轨50%断裂检测点处振动加速度频谱图Fig.7 Vibration acceleration frequency spectrum at the detection point of the rail semi-fracture

图7中可以明显发现，在频谱图中更能清晰地分析钢轨在周期荷载激振力作用下，钢轨在整个过程中振动加速度的变化情况。在检查点1 处：1) 整体来看，幅值的平均值为：502.7 mm/s2，相比无缺陷轨道检测点1 处幅值平均值提高了33.2%；2) 幅值在120 Hz 时达到最大为5 763.2 mm/s2，相比无缺陷轨道检测点1 处峰值提高了72.1%；对于检测点2 而言：1) 幅值的平均值为：46.7 mm/s2，相比无缺陷轨道检测点2 处幅值平均值下降了62.7%；2) 幅值则在120 Hz 时达到最大为684.7 mm/s2，相比无缺陷轨道检测点2处峰值下降了66.2%。出现上述的情况可以通过振动波的传递会受钢轨的黏滞特性的影响的角度来分析其合理性。振动波在钢轨内部不同质点有不同速度时，会引起相对运动，于是便产生了阻力，阻力的大小与钢轨的长度，接触面积以及质点的速度差成正比，因此当钢轨截面发生50%断裂时，相比无缺陷轨道，检测点1处的钢轨接触面积变小了，长度也变短了，因此在检测点1端的振动加速度幅值便会增大。由于钢轨的半断裂，振动波并没有完全传递到检测点2端的钢轨，因此在该端的振动加速度幅值会有所减小。

3.2.2 钢轨截面全断裂

1) 加速度时域分析轨道缺陷为钢轨截面全断裂时，钢轨的振动加速度时域曲线如图8所示。

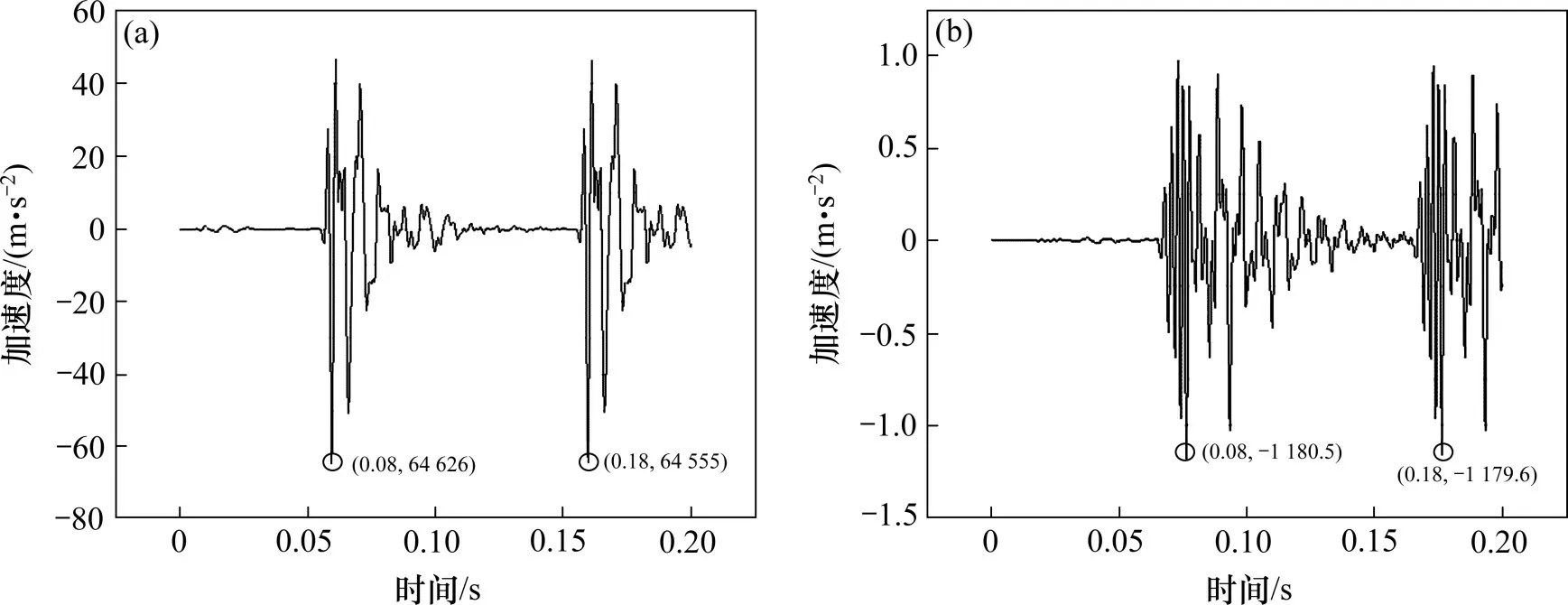
图8 钢轨全断裂检测点处振动加速度时域曲线Fig.8 Time-domain curve of vibration acceleration at the detection point of the rail complete fracture

如图8所示，在钢轨有全断裂的情况下，钢轨在检测点1处的振动加速度保持与正常轨道相似的周期性振动特征，在0.06 s，振动加速度达到最大值为64 626.2 mm/s2，比无缺陷轨道同一点处峰值提高了35.1%；而在检测点2 处，在0.08 s，振动加速度达到最大值为1 180.5 mm/s2，比无缺陷轨道同一点处峰值下降了89.8%，这是由于钢轨全断裂，振动波传播到钢轨断裂处大部分会被反射，无法正常传播到检测点2端的钢轨，从而导致检测点2处的钢轨振动加速度出现大幅度下降但在周期荷载的作用下，地基也会有少许振动，以至于没有完全降为0。

2) 加速度频谱分析轨道缺陷为钢轨截面全断裂时，钢轨的振动加速度频谱如图9所示。

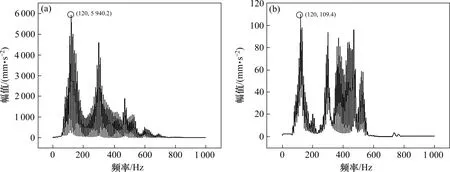
图9 钢轨全断裂检测点处振动加速度频谱图Fig.9 Vibration acceleration frequency spectrum at the detection point of the rail complete fracture

从图9的频谱图的观察中能够得到，在检测点1 处：1)整体来看，幅值平均值为：529.18 mm/s2，相比无缺陷轨道检测点1 处幅值平均值提高了40.3%；2) 在频率为120 Hz 时幅值达到最大为5 940.8 mm/s2，相比无缺陷轨道检测点1 处幅值提高了77.5%。在检测点2 处：1) 幅值的平均值为：13.8 mm/s2，相比无缺陷轨道检测点2 处幅值平均值下降了89.0%；2) 在频率为120 Hz 时幅值达到最大为109.4 mm/s2，相比无缺陷轨道检测点2处幅值下降了94.6%。出现上述情况是由于检测区域内某处钢轨出现了完全断裂，相当于钢轨的长度分成了两部分，长度上明显变短，因此振动波在钢轨中的传播阻力变小，且在钢轨断裂截面会反射回大量振动波，从而导致了在检测点1处钢轨振动加速度的大幅上升。另一方面可以通过能量守恒的角度分析其合理性，在一定的周期内，外来荷载作用在钢轨上，钢轨受迫振动产生的能量也就一定，在钢轨截面出现完全断裂后，振动波无法正常传播到检测点2端的钢轨，于是对比无缺陷轨道在同样条件下，钢轨截面完全断裂后检测点1处的振动能量大幅提高，而检测点2端的振动能量会大幅下降。

4 结论

1) 运用振动理论，提出了一种新型的钢轨缺陷检测方法。该种检测方法直接将钢轨本身的振动响应作为判断依据，而不是以车辆响应作为判断依据，可以不考虑转向架悬挂系统的影响，相比于基于车辆振动响应的钢轨损伤检测方法，该检测方法具有成本低廉，简单方便，可行性高，且不会对轨道本身造成负面影响等优点。

2) 通过仿真对比实验验证了模型的可靠性。得到了不同轨道缺陷对应的振动特征规律，并进行了多组仿真实验误差均在5%以内，验证了该种检测方法的可靠性。最后得到了在幅值为85 kN 的周期载荷激励下，以无缺陷钢轨的数据作为参考基础，不同钢轨缺陷条件对应的振动特征，总结如下：首先整体宏观来看，检测点1处的振动频域的幅值平均值出现明显上升，且检测点2处的幅值平均值出现明显下降，可推测检测区域钢轨存在断裂隐患。进而对频谱图进行细节分析：①在钢轨振动加速度频谱图中，若检测点1处的振动幅值明显升高，升高幅度约为72.1%，而检测点2 处振动幅值有一定的下降，下降幅度约为67.1%，则可推断检测区域的钢轨大概率存在严重裂缝或50%断裂损伤缺陷；②若检测点1 处，振动的幅值提高，升高幅度约为77.5%，而检测点2 处的振动的幅值出现大幅度下降，下降幅度约为94.6%，则可推断检测区域钢轨截面存在完全断裂；其余荷载作用下均可遵循本方法，得出不同钢轨缺陷相对应的振动特征。

本方法还可以用来研究其他轨道缺陷以及组合缺陷的振动规律特性，最终可将各振动规律特性汇总，通过大数据信息融合形成一套完整的轨道检测设备，具有较高的工程利用价值。