基于生成对抗网络的三维频谱态势补全

胡田钰，吴启晖，黄 洋，2

（1.南京航空航天大学电子信息工程学院，南京 211106；2.东南大学信息科学与工程学院，南京 211189）

引 言

近年来，随着中国空天地信息网络一体化的不断发展，卫星网络与地面移动网络已作为常态化基础网络存在，而各类基于无人机或其他空中平台的中继网络则将组成天地之间的机动网络，通信系统正迎来从地面5G到航空6G这一6G基础形态的重大演进［1‑2］。但随着空天地信息网络中无线智能终端和业务数量的急剧增长，日益稀缺的频谱资源与已分配频谱资源利用不足之间的尖锐矛盾也愈发突出［3‑4］。因此，急需研究适用于空天地信息网络的认知无线电（Cognitive radio，CR）技术，以提高三维电磁频谱空间的频谱利用率。

CR将无线通信网络中的用频设备分为主要用户（Primary users，PUs）和次级用户（Secondary us‑ers，SUs）［5‑6］。对于地面通信系统，常用的一种表征当前区域内频谱资源使用情况的CR技术是将SUs所获取的信号功率谱密度（Power spectrum density，PSD）等无线电参数的分布情况进行可视化，“有的放矢”地实现频谱预测、频谱决策和频谱管控等多种应用，以提高通信系统频谱资源利用率。该可视化方法通常被称为频谱地图或无线电（环境）地图［7‑9］。但是，该方法仅考虑PSD在地理位置上的二维分布情况，不能简单直接地套用于空天地信息网络。

因此，本文将对PSD在三维空间上的时空频分布情况的表征进行研究，并以“频谱态势”来指代该分布情况。三维频谱态势使人们可以查看任何时间和三维位置的准确PSD分布，从而提高频谱资源在时间和空间维度上的利用率［10］。但在三维电磁频谱空间中，受限于SUs的空间部署、监测频段以及监测时间段等因素，所构建的三维频谱态势在时域、空域和频域等维度上往往是离散且缺损的。如图1所示，在三维目标区域中，PUs占用频谱资源并进行信号发射，但PUs的位置信息、发射PSD等未知；而进行信号接收的SUs所在位置和接收PSD则已知。因此，此时通过SUs的实测频谱数据只能得到缺损三维频谱态势。所以，三维频谱态势构建的基本任务和主要难点便在于利用现有实测数据和PSD时空频相关性，对三维频谱态势进行精确补全，以形成可供系统使用的补全三维频谱态势，其理想补全示例如图2所示。对于常用于二维频谱地图补全的插值方法，例如反距离加权（Inverse distance weighted，IDW）算法，虽然可以扩展至三维频谱态势补全，但该算法只考虑距离因素，实际中往往因为缺乏模型验证而导致补全效果不佳［10‑11］。本文将专注于三维频谱态势的精确补全，并借助备受关注的生成对抗网络（Generative adversarial networks，GANs）技术来实现［12］。

图1 三维目标区域的主要用户和次级用户分布示例以及主要用户的功率谱密度示例（f 1为中心频率，f max和f min分别为频率最大值和最小值）Fig.1 Example of the deployment of PUs and SUs in a three-dimensional target area and an example of power spec‑trum density of a PU(where f 1,f max and f mi n are the center frequency,the maximum frequency and the mini‑mum frequency,respectively)

图2 工作频率为f 1时的目标区域三维频谱态势的理想补全示例Fig.2 Ideal completion example of the three-dimensional spectrum situation of a target area when the working fre‑quency is f 1

GANs旨在生成足以与真实样本相比拟的模拟样本，当网络训练收敛时，GANs所生成的模拟样本几乎可以认为服从于真实数据分布，即能做到“以假乱真”［13‑16］。因此，文献［17］以若干不同频率下的完整频谱地图作为训练数据，通过转换频谱地图为RGB彩色图像的数据预处理方法，利用所提出的图估计GAN（Map estimation GANs，MEGAN）结构学得频谱地图补全机制，最终输出补全后的频谱地图。但文献［17］仅关注二维的底层认知无线电网络，并未对三维电磁频谱空间展开进一步研究。文献［18］虽然提出了一种对三维频谱态势补全性能与无人机部署耗能进行联合优化的三维频谱感知框架，但其仅利用传统图像恢复方法在不同维度进行切片平均来实现三维补全。总的来说，在三维电磁频谱空间中，利用GANs实现精确的三维频谱态势补全的相关研究还未见报道。

为了进一步提高三维频谱态势补全的精确性，本文针对三维电磁频谱空间提出了一种基于生成对抗网络的三维频谱态势补全算法，具体工作如下：

（1）利用生成对抗网络在三维电磁频谱空间展开研究，利用新兴的生成对抗网络实现三维频谱态势补全，为构建高精度数字孪生频谱空间打下坚实基础。

（2）提出了一种具备U形结构的三维条件生成对抗网络（Three‑dimensional U‑shaped conditional generation adversarial network，3D‑UCGAN），该结构能从包含完整三维频谱态势的训练数据中提取更符合三维电磁频谱空间环境特征的有用信息。

（3）提出了一系列改进三维频谱态势补全性能的数据处理方法，主要包括3D‑UCGAN的输入数据预处理以及输出数据再处理。

通过仿真可以得到如下结论：所提出的基于生成对抗网络的三维频谱态势补全算法的性能优于传统基于插值的补全算法；所提出的3D‑UCGAN结构能有效地降低本文算法的补全误差和训练时间；所选择的数据预处理方法可以进一步加速网络收敛速度。

1 系统模型

1.1 三维频谱态势补全模型

现代无线通信的基础设施由部署在三维空间的异构无线网络组成，因此目标区域的三维频谱态势是由该区域内若干异构网络同时进行的无线传输叠加形成，进而呈现出信号功率谱密度在不同位置、频率和时间上的不规则变化情况［10］。因此，将三维频谱态势Ψ(x，f，t)定义为三元组变量(x，f，t)到信号功率的一种映射关系，其中x∈R3表示通信系统在使用三维频谱态势时所查看位置的三维坐标(xl，xw，xh)，而f和t则分别表示所查看的特定时间和工作频率。但为了进一步简化模型，在后续的讨论中忽略变量t。

对于长宽高为L×W×H的三维目标区域A，将其进行栅格化，把三维目标区域A分为NL×NW×NH个栅格。后文中的位置坐标均代表栅格的位置坐标。但当栅格划分较稀疏时，很可能某栅格内存在多个接收SUs。因此，如果栅格x处存在Nx个接收SUs，则将这Nx个SUs接收功率谱的平均值视为该栅格在频谱态势上展现的接收功率谱。经该数据栅格化处理后，可假设三维目标区域A中均匀分布着NR个数量已知的接收SUs，且此时每个栅格中至多存在1个接收SU；而同时存在着NT个数量未知的发射PUs。

1.2 信号传播模型

本节将对传播规律ΓxT，i→x(f)进行建模，即建立三维目标区域的信号传播模型。对于第i个PU所发出的频率为f的信号，假设其从位置xT，i传播到任一其他位置x时的路径损耗P L(d)为

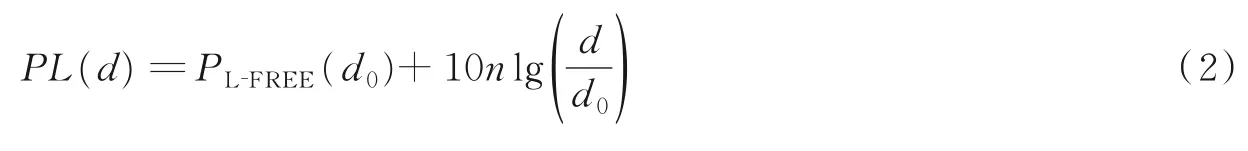
式中d为位置xT，i与位置x间的距离，d0为计算时的参考距离，n为路径损耗因子，PL‑FREE(d0)为参考距离d0下的自由空间传播损耗［19‑21］。因此，对于第i个PU的发射信号，位置x处的接收功率为

2 基于生成对抗网络的三维频谱态势补全

本节首先简要介绍了GANs的基本概念以及学习机制。其次，提出了基于GANs的三维频谱态势补全算法，并对数据处理方法进行了一定的改进。进一步地，为了提高GANs对三维频谱态势的学习能力，提出了一种面向三维频谱态势补全的3D‑UCGAN结构，并将该结构应用于所提算法中。

2.1 GANs基本概念与学习机制

GANs主要由生成器网络和鉴别器网络组成［22］，其中生成器网络G(z；θg)在参数（即网络中各神经元的权重与偏置）θg的作用下，将潜变量z~pz(z)转换为与真实样本s~pdata(s)规格相同的模拟样本ŝ，即G(z；θg)=ŝ；且样本ŝ服从生成器网络对分布pdata(s)隐式建模得到的分布pg(ŝ)［12］。而鉴别器网络D(s；θd)或D(ŝ；θd)则在参数θd的作用下，判断输入样本s或ŝ服从于分布pdata(s)而不是分布pg(ŝ)的可能性［12］。

GANs旨在学习数据分布pdata(s)，并采用生成器网络和鉴别器网络相互对抗的训练策略来实现。针对鉴别器网络，该策略最大化其正确鉴别的概率，而针对生成器网络则最大化鉴别器网络鉴别出错的概率。进而在不同鉴别结果的反馈下，不断提升网络鉴别/生成能力。假如具备足够的网络容量，则鉴别器网络和生成器网络可实现动态平衡。此时生成器网络隐性建模得到的分布pg(ŝ)收敛于分布pdata(s)，而鉴别器网络不能正确地区分样本s和ŝ。

2.2 基于GANs的三维频谱态势补全算法

所提出的基于GANs的三维频谱态势补全算法共包括离线训练阶段和在线部署阶段，其中“在线”和“离线”均针对所使用的GANs而言。进一步地，算法中不仅包括与GANs相关的流程，还包括各阶段所必需的数据处理方法，其将更有利于GANs训练与态势补全。需要说明的是，在算法实际运行时，所使用的GANs结构为2.3节提出的3D‑UCGAN结构。在离线训练阶段，借助深度学习（Deep learning，DL）数据驱动的特点［22］，以完整频谱态势数据作为训练数据对GANs进行训练。而对于算法在线部署阶段，借助深度学习低复杂度的特点［22］，将已训练至收敛的生成器网络部署于实际应用，直接根据SUs的测量结果对实际缺损三维频谱态势进行精确补全。所提出的基于GANs的三维频谱态势补全算法的流程如图3所示。

图3 基于3D-UCGAN的三维频谱态势补全算法流程图Fig.3 Procedure of three-dimensional spectrum situation completion algorithm based on 3D-UCGAN

GANs学习缺损三维频谱态势至补全三维频谱态势的补全机制，也即以缺损三维频谱态势作为条件的完整态势数据分布。具体而言，在GANs的对抗训练过程中，网络参数θg和θd在目标函数的指导下，经基于梯度的学习算法不断迭代更新，以至于网络的鉴别能力或生成能力在不断提升。因此，生成器网络在输入缺损三维频谱态势的情况下，不断朝着输出补全三维频谱态势近似于对应完整三维频谱态势的方向进行学习；而鉴别器网络则在输入完整/补全三维频谱态势的情况下，朝着正确鉴别此时输入态势真假的方向进行学习。进而GANs逐步达到生成器隐性建模分布接近于态势数据分布的预期效果，并最终实现收敛。

（1）离线训练阶段

本文所提出的数据预处理方法基于灰度进行。具体而言，在离线训练阶段，首先将每组完整三维频谱态势切片进行归一化处理，即得到灰度模式下的一通道完整三维频谱态势“灰度图”（数据维度：1×NL×NW×NH），如图4（a）所示。进一步地，将一通道三维频谱态势“灰度图”扩充为三通道的完整三维频谱态势“灰度图”（数据维度：3×NL×NW×NH），其中每通道的频谱数据仍与原一通道时的数据相同。同时还对一通道三维频谱态势“灰度图”以采样率α进行采样，即上文所述的随机选取SUs位置。随后，以相同方式对该采样数据扩充为三通道，并对未采样点以除黑白灰色以外的颜色进行重新着色，得到三通道的缺损三维频谱态势“彩色图”。本文选取红色对未采样点进行着色，如图4（b）所示。因此，在经过数据预处理后，可得到三通道的完整三维频谱态势“灰度图”和缺损三维频谱态势“彩色图”，其将作为训练数据用于后续GANs的训练中。需要说明的是，文献［17］提出一种基于RGB的数据预处理方法，其直接将归一化数据经RGB色谱图进行颜色映射。但该方法仅针对量化离散的频谱数据进行，极有可能在颜色（逆）映射时丢失信息，反而增加补全误差。因此，本文并未采用该方法，并且不同数据预处理方法所带来的算法补全性能影响将在第3节给出。

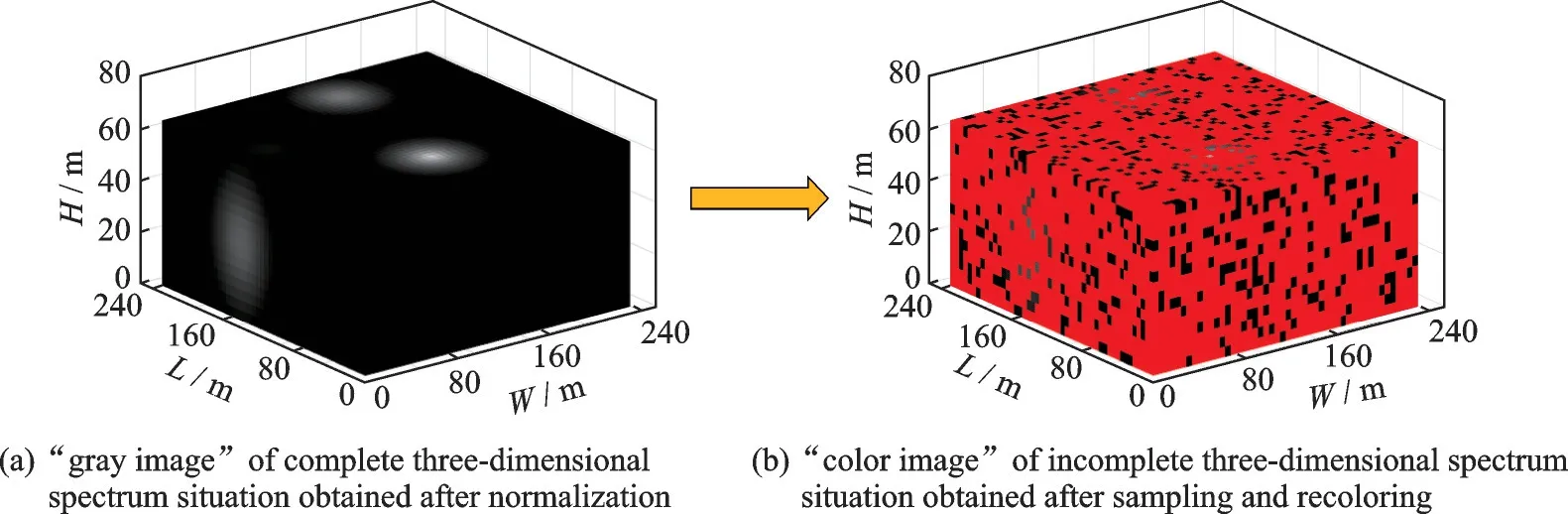
图4 工作频率为f 1时的目标区域完整三维频谱态势的数据预处理示例Fig.4 A data preprocessing example of complete three-dimensional spectrum situation of a target area when the work‑ing frequency is f 1

（2）在线部署阶段

该阶段把已训练好的生成器网络部署到实际应用，例如面向航空6G的频谱认知智能管控体系架构中的频谱云模块［1］。设定实际应用时的频谱数据为SUs实测获得的缺损三维频谱态势，且同样需要进行数据预处理。但该阶段的数据预处理方法与离线训练阶段所用方法有些许差别。首先，对于数据归一化，SUs很可能不会刚好放置于三维目标区域内接收功率最大值/最小值所在栅格处。因此，将以往实测接收功率的最值与此次实际应用时的数据最值进行比较，并取其更大/小值，以尽量避免数据处理误差。其次，将不再进行离线训练阶段数据预处理方法中的采样步骤，而是直接对扩充为三通道的缺损三维频谱态势“灰度图”的未采样点进行重新着色。

2.3 面向三维频谱态势补全的3D‑UCGAN结构

（1）训练框架

由于基本GANs的代价函数存在一定的缺陷，其训练过程经常出现不稳定的现象［15］。因此，还引入文献［16］提出的带有梯度惩罚项的Wasserstein GAN（Wasserstein GAN with gradient penalty，WGAN‑GP）框架。不同于文献［12］所采用的JS（Jensen‑Shannon）散度，WGAN‑GP中使用Lipschitz约束下的Wasserstein距离作为代价函数，以此减轻网络训练时的不稳定性。

因此，通过所引入的CGAN和WGAN‑GP框架，确定了面向三维频谱态势补全的3D‑UCGAN结构的训练目标

式中：V(D，G)为GANs的代价函数；λ=10为惩罚因子；Ψ'为用于计算式（4）中最后一项（即惩罚项）的样本，而分布pgp(Ψ')通过对与分布pdata(Ψ)和分布pg(Ψ̂)相关的点对均匀采样而得到［16］。具体而言，样本Ψ'由两部分相加组成，其中一部分是真实样本Ψ乘以一随机数ϵ~u(0，1)，另一部分则是模拟样本Ψ̂乘以(1-ϵ)。面向三维频谱态势补全的3D‑UCGAN结构的训练框架示意图如图5（a）所示，图5（b）则展现了训练过程中样本Ψ'的实现方式。

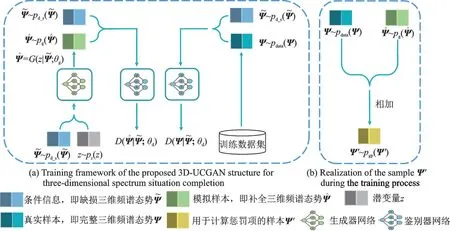
图5 3D-UCGAN结构的生成对抗机制Fig.5 Generative adversarial mechanism of the proposed 3D-UCGAN structure

（2）网络搭建

三维频谱态势补全问题的实质在于对每个未布置SU的栅格处频谱数据进行补全。因此，借用DL领域中像素级语义分割的概念［23］，同样可以将三维频谱态势补全视作“像素级补全”。因此，在面向三维频谱态势补全的生成器网络中引入一种经典的语义分割网络，即具备U形结构的网络（U‑shaped net，U‑net）的搭建思想［24］。具体而言，先采用三维卷积层进行下采样，以实现电磁频谱空间的环境特征提取；再采用三维转置卷积层进行上采样，以恢复态势尺寸，并获得每个栅格的补全信息；同时将上采样和下采样过程中对应层的输出三维特征图在通道维度进行拼接，以实现多尺度特征融合。

因此，将所提出的面向三维频谱态势补全的GANs结构称作3D‑UCGAN，其生成器网络结构如图6所示，其中每层网络为三维卷积层或三维转置卷积层，共6层。图中hl=(k，s，p)指第l层的卷积核大小k、计算步长s和补零层数p等超参数的设置情况。而当l=0，…，5时，Fl指网络中第(l+1)层的输入数据通道数；而当l=6时，Fl则指生成器网络输出层（即第6层）的输出数据通道数。3D‑UCGAN的鉴别器网络如图7所示，其中每层网络为三维卷积层或全连接层，共4层。不同于文献［17］，本文不仅通过减少网络层数的方式来降低训练复杂度，还以条件信息（即缺损三维频谱态势）作为额外的输入来提升网络的鉴别能力。图中hl=(k，s，p)仍指第l层卷积层的超参数设置情况。当l=0，…，2时，F l指网络中第(l+1)层卷积层的输入数据通道数；而当l=3时，Fl则指鉴别器网络第3层卷积层的输出数据通道数。

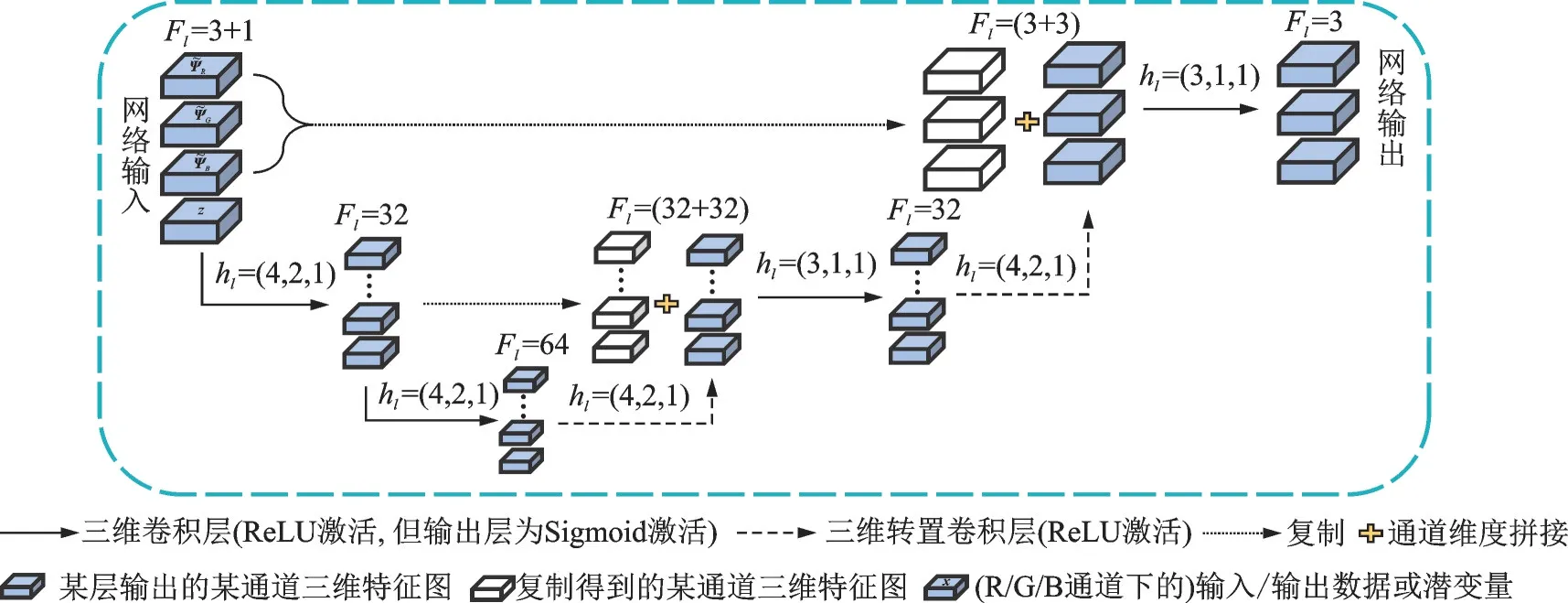
图6 3D-UCGAN结构的生成器网络Fig.6 Generator network of 3D-UCGAN structure

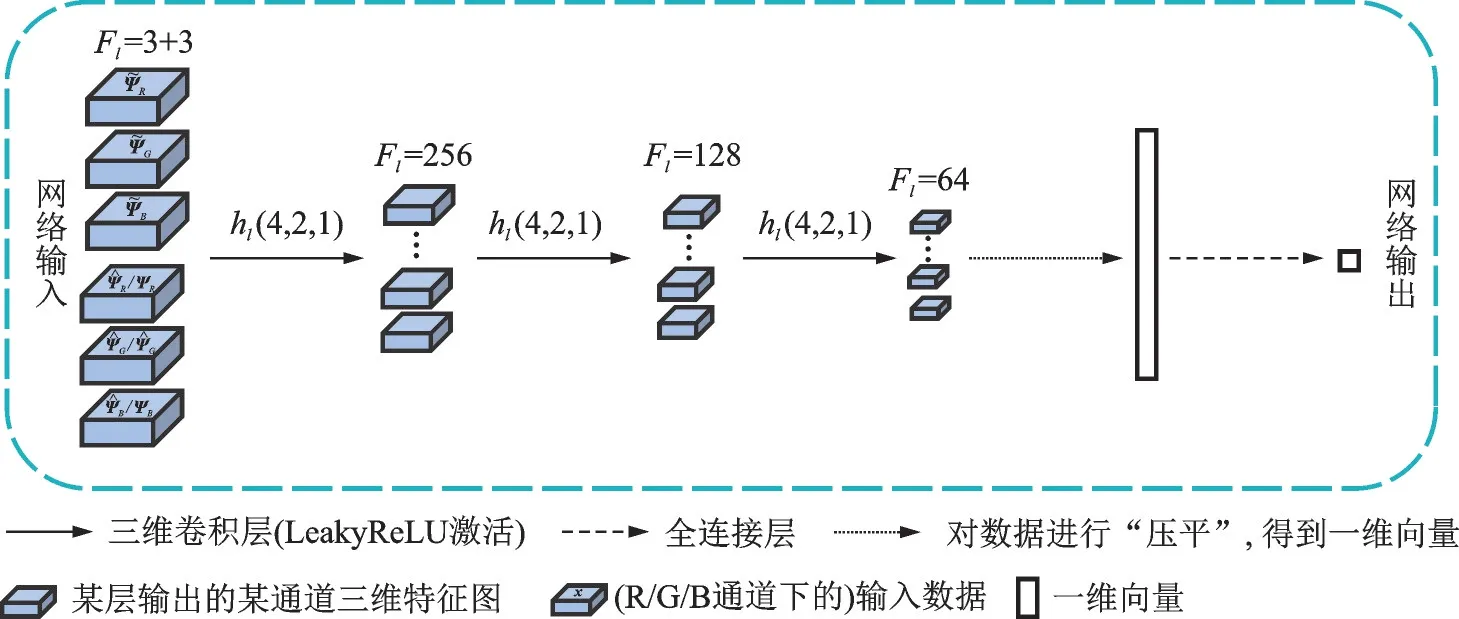
图7 3D-UCGAN结构的鉴别器网络Fig.7 Discriminator network of 3D-UCGAN structure

3 性能评估

本节通过仿真测试对所提出的基于3D‑UCGAN的三维频谱态势补全算法的性能进行评估。基于Python3.7.0的Pytorch 1.0框架建立了3D‑UCGAN模型，并在Nvidia GeForce RTX 2080图形处理单元上进行该模型的训练和测试工作，以实现算法的离线训练和在线部署阶段。

基于本文建立的系统模型，设定三维目标区域A的大小为L×W×H=240 m×240 m×80 m，并将其分为NL×NW×NH=48×48×16个栅格，即每栅格为体积为5 m3的立方体。同时，设定PUs数量NT从1~5中随机选择，而次级用户数量NR默认为5 504个，即采样率α≈15%。对于信号传播模型，假设参考距离d0=0.01 km，频率f∈(25 MHz，125 MHz)，即三维频谱态势切片Ψ(x，f)，∀x∈A的频率所属范围。

对于算法的离线训练阶段，设置30 000组三维频谱态势切片Ψ(x，f)，∀x∈A作为3D‑UCGAN的训练数据，并使用自适应矩估计（Adaptive moment estimation，Adam）算法作为3D‑UCGAN的学习算法。同时，设置3D‑UCGAN中生成器网络和鉴别器网络的学习率为0.000 1，批训练大小为4，训练轮数为20。进一步地，为了提高3D‑UCGAN的泛化能力，在训练数据中，设置每10 000组数据的路径损耗因子和噪声功率（单位：mW）是不同的，依次为n=8、σ2=10-5，n=4、σ2=10-5，n=4、σ2=10-3。需要说明的是，为了使SUs在不同频率下的接收功率更符合实际情况，设定每组频谱数据的发射功率（单位：mW）随机从向量[67，467，867，1 000，1 000，1 000，867，467，67]中进行抽取（即假设SUs工作频率与PUs中心频率可能不一致的情况）。而对于算法的在线部署阶段，使用10 000组三维频谱态势切片Ψ(x，f)，∀x∈A作为测试数据，其中路径损耗因子n=6和噪声功率σ2=10-5mW，其余设置与训练数据相同。注意，利用L2损失函数，即均方误差（Mean squared error，MSE）来评价每组训练/测试数据的态势补全性能，其计算公式为

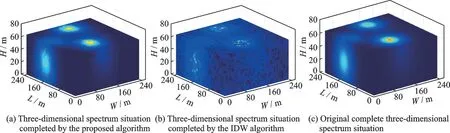
图8 随机选取的某次测试三维频谱态势补全结果Fig.8 Three-dimensional spectrum situation completion results of a randomly selected test

其次，为了验证本文所提出的3D‑UCGAN结构对三维频谱态势补全算法的性能提升，将其与基于文献［17］经卷积层扩展后的3D‑MEGAN结构进行对比。在所提出的基于GANs的三维频谱态势补全算法中，分别基于3D‑UCGAN与3D‑MEGAN结构执行算法的离线训练和在线部署阶段，并在图10中对两种结构在不同训练轮数时的平均MSE进行比较，其中针对训练数据的MSE被称作训练误差。从图10中可以看出，无论关注于训练误差还是测试误差，基于3D‑UCGAN结构的频谱态势补全算法在训练轮数为1或2时就已经收敛；但对于3D‑MEGAN结构，其在训练轮数大于12时才趋于收敛。并且，3D‑UCGAN结构下的算法补全误差小于3D‑MEGAN结构下的补全误差。因此，所提出的3D‑UCGAN结构能有效降低频谱态势补全算法的补全误差和训练时间。

图9 所提算法与IDW算法于不同采样率时的三维频谱态势补全性能的对比Fig.9 Comparison of three-dimensional spec‑trum situation complement performance between the proposed algorithm and the IDW algorithm at different sampling rates

图10 基于3D-UCGAN结构与基于3D-MEGAN结构的三维频谱态势补全算法于不同训练轮数时的性能对比（采样率α=15%）Fig.10 Performance comparison of three-dimensional spectrum sit‑uation complement algorithm based on the 3D-UCGAN structure and the 3D-MEGAN structure at different train‑ing epochs(sampling rateα=15%)

最后，通过所提出的基于3D‑UCGAN的三维频谱态势补全算法，图11和图12分别对所提出的数据预处理和再处理方法下的算法补全性能进行了探讨。从图11可以看出，基于RGB的数据预处理方法大大减慢了3D‑UCGAN的训练收敛速度，以至于当训练轮数达到20时，其训练误差仍大于基于灰度预处理时的最大训练误差。因此，本文所提出的基于灰度的数据预处理方法能进一步加快网络训练的收敛速度，且无须进一步比较不同数据预处理方法下的测试误差情况。而由于数据再处理方法运用在算法的离线部署阶段，因此本文在图12中只比较了不同数据再处理方法下的测试误差情况。从图12中可以看出，所提出的数据再处理方法确实能较好地对频谱态势的补全精度进行改进。

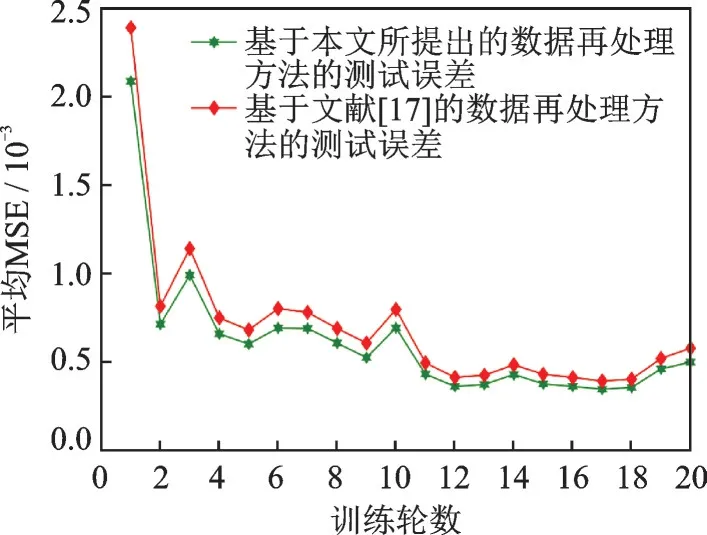
图12 基于所提再处理方法与基于文献[17]再处理方法的三维频谱态势补全算法于不同训练轮数时的性能对比（采样率α=15%）Fig.12 Performance comparison of three-dimensional spectrum situation complement algorithm based on the proposed post-processing method and the method in Ref.[17]at different training epochs(sampling rateα=15%)

4 结束语

本文对三维电磁频谱空间的频谱态势补全问题进行了充分探索，所提出的补全方法可以有效地降低态势补全误差，以辅助通信系统在目标区域内提升频谱利用率。仿真结果证明，本文所提出的三维频谱态势补全算法在态势补全精度方面优于传统基于插值的方法，并且可以在较短的网络训练时间下得到能对缺损频谱态势进行精确补全的生成器网络。