一种TR‑OFDM系统的四元数加密算法

陈善学，杜文正，冯叶青，李方伟

（重庆邮电大学通信与信息工程学院，重庆 400065）

引 言

随着无线通信技术的迅猛发展，人们对通信的速率和安全也提出了更高的要求。而根据通信理论，二进制数据传输的速度首先取决于基带的调制方式，通常调制方式越高数据传输速率越快，但其调制的各个参数（振幅、相位和频率）之间的相互影响也越严重，误码率也越高，要保障其传输质量只能通过提高信噪比或采用更加复杂的接收技术。而高维信号在信号能量相等的情况下，可以实现更低的误码率并且可以在实际环境中实现更加高效和可靠的通信［1⁃2］。同时物理层中由于信道固有的开放性与广播性，使得物理层成了通信系统中最脆弱的一环，因此物理层安全也引起了学术界的广泛研究。物理层安全中的星座旋转是一种调整信号星座使窃听者无法正确解码接收到的信息的技术［3］，目前对于调制信号的加密方式主要有相位旋转［4］、幅相变换［5］和星座间跳转［6］。而文献［5⁃6］复杂度较高，实现起来比较困难。文献［7］对调制信号进行星座旋转并添加少许人工噪声以保证OFDM系统的安全，但人工噪声会降低信道资源的利用率，文献［8⁃9］研究了QPSK信号的三维星座设计并推导了三维星座点的误码率。文献［10⁃11］设计了高阶的三维信号星座，相比于传统的二维星座，三维星座可以在相同信号能量前提下降低误码率。而传统的调制方式，随着调制阶数的增大，星座信号之间的最小欧式距离（Minimum euclidean distance，MED）逐渐减少，致使信号在信道中的鲁棒性受到了损害，信号的误码率开始逐渐增大，而三维星座可以在相同误码率的前提下实现更高的吞吐量，并且提高了信号的鲁棒性。这使得三维信号星座在提高信息传输速率方面具有重大的潜力，尤其是对于数据较大的文件（如音频、视频和压缩包等）的传输具有重大意义。而文献［12］将三维星座分别绕x轴、y轴和z轴旋转不同的角度，这种算法每个星座点需要依次乘以3个三维旋转矩阵，空间复杂度太高。而四元数可以实现绕任意轴的旋转［13⁃14］，且其所需的内存远小于3个三维旋转矩阵。而时间反演（Time reversal，TR）等效于一个空时匹配滤波器，可以降低OFDM系统的误码率，减小循环前缀长度。故本文针对TR⁃OFDM系统，提出了一种四元数加密的物理层加密传输算法。

1 系统模型

本文的TR⁃OFDM系统模型主要有3个节点，如图1所示：基站是Alice，合法用户Bob，而Bob附近有一个潜在的窃听者Eve，Eve的位置和信道状态信息未知。Bob和Eve都只配备一根天线，基站Alice与合法用户Bob需要实现安全传输通信。设Alice到Bob之间的信道为主信道，Alice与Eve之间的信道为窃听信道。假设Alice和Bob采用时分双工（Time division duplex，TDD）通信模式，通信双方Alice和Bob利用估计到的信道状态信息生成加密和解密所需的四元数。根据本文所采用的安全传输模型，采用N个子载波传输的传输OFDM符号。主信道和窃听信道都是瑞利多径信道。

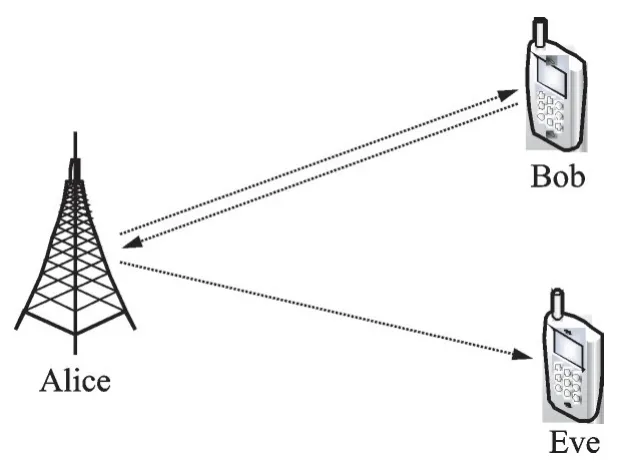
图1 系统模型Fig.1 System model

2 四元数加密算法

三维TR⁃OFDM系统如图2所示。

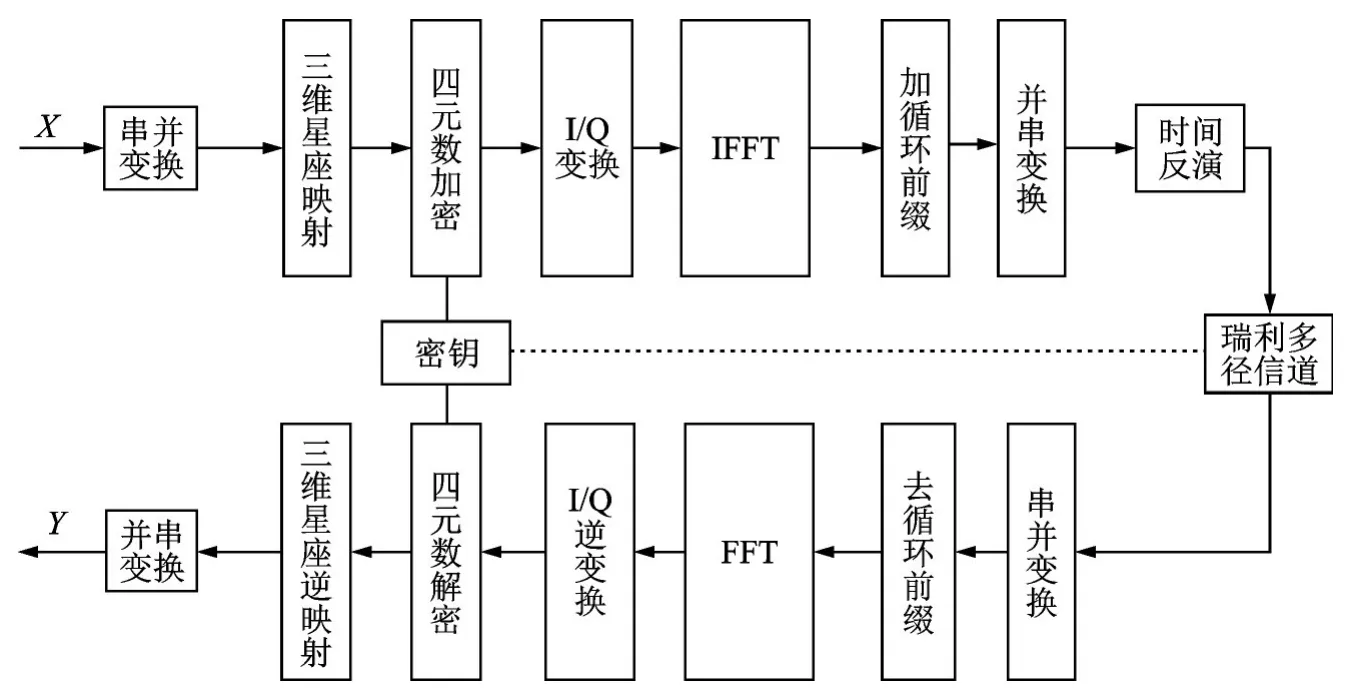
图2 三维TR⁃OFDM系统方框图Fig.2 Block diagram of three⁃dimensional TR⁃OFDM system

假设Alice需要传输一组比特序列，先将二进制序列进行串并变换，然后把每M个比特映射为一个三维的信号si=[xiyizi]T。将每个三维星座点进行四元数加密后的星座点s'i=[x'iy'iz'i]T表示为

式中：q为四元数，q=[q0q1q2q3]，s'i等效于三维星座点si绕轴n旋转θ后的三维星座点。

图3是加密前4⁃ary的三维星座点，4个三维星座点均匀分布在一个半径为1的球面上，并且4个点刚好构成一个正四面体。图4是加密后4⁃ary的三维星座点，三维星座点经过四元数加密，随机地分布在半径为1的球面上。图5是加密前16⁃ary的三维星座点分布，16个点分别在两个不同半径的球面上，每个球面上8个点，而且每个球面上的8个点刚好构成一个正方体。图6是加密后16⁃ary的三维星座点分布，16⁃ary的三维星座点经过旋转加密后，随机地分布在两个球的球面上。接着对加密过的信号s'i=[x'iy'iz'i]T进行I/Q变换（I：同相分量，Q：正交分量）。加密过的信号s'为

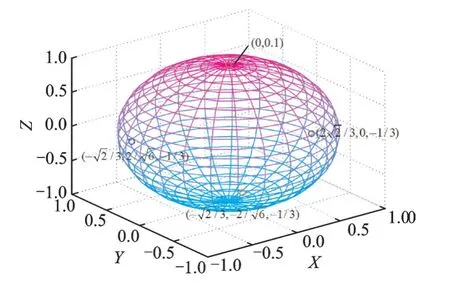
图3 加密前的三维信号（4⁃ary）Fig.3 Three⁃dimensional signal before en⁃cryption(4⁃ary)

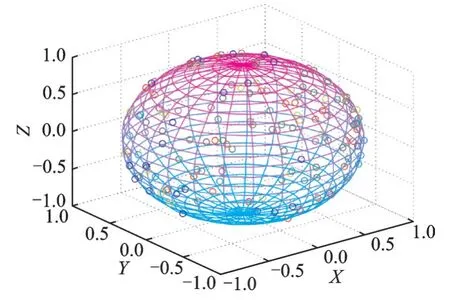
图4 加密后的三维信号（4⁃ary）Fig.4 Three⁃dimensional signal after encryp⁃tion(4⁃ary)

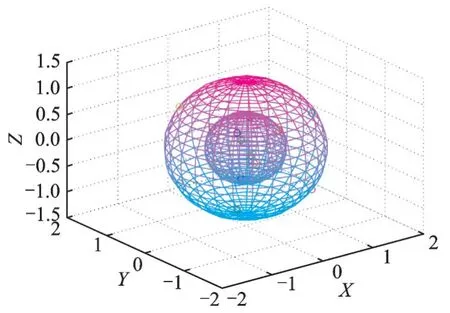
图5 加密前的三维信号（16⁃ary）Fig.5 Three⁃dimensional signal before encryption(16⁃ary)

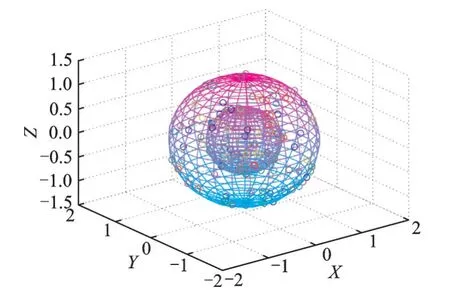
图6 加密后的三维信号（16⁃ary）Fig.6 Three⁃dimensional signal after encryption(16⁃ary)

I/Q转换后的信号s''为

将信号s''进行快速傅里叶逆变换（Inverse fast fourier transform，IFFT），为了消除载波间的干扰和符号间干扰加入循环前缀，在并串变换后通过时间反演操作后发送出去。Bob第k个子载波上接收到的频域信号为

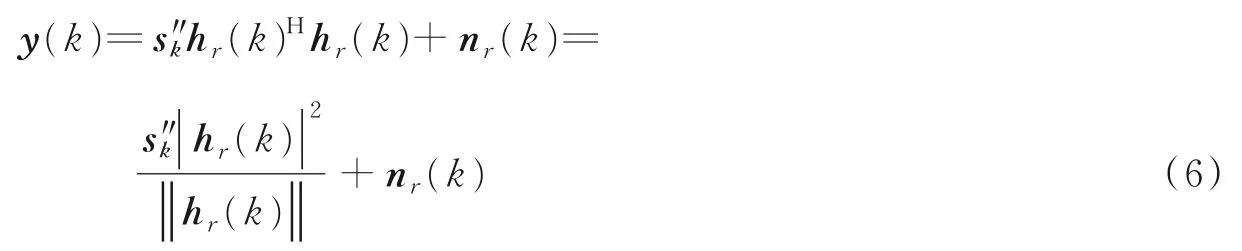
式中：hr(k)为Alice和Bob之间的信道的第k个子载波的频域冲激响应；hr(k)H为时间反演镜，它是主信道在频域的共轭；nr(k)是均值为0、方差为σ2的加性高斯白噪声。

式中：L为多径总数，αl为第l条多径的幅度值，Δf为子载波间隔，τl为第l条多径的时延。

Bob接收到信号后对接收到的信号进行一系列处理（串并变换，傅里叶变换（Fast fourier tansform，FFT），去循环前缀）后进行阈值判决，即可得到聚焦的有用信号

接着将信号s''进行I/Q逆变换，重新映射为N行3列的三维星座点

与发送端相对应，Bob利用四元数对接收到的信号进行解密，也就是对三维星座点绕与n对称的轴旋转θ，进行旋转解密后的信号为si。

解密后的三维星座点，利用最小距离检测器，对接收到的信号进行解调得到初始的比特信息。

Eve第k个子载波上接收到的频域信号为

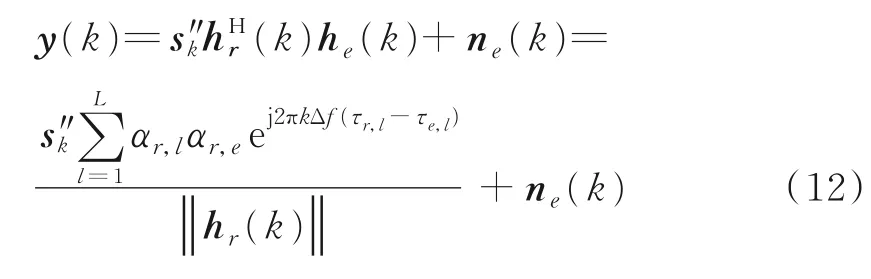
式中：he(k)为Alice和Eve之间的信道的第k个子载波的频域冲激响应，ne(k)是均值为0方差、为σ2的加性高斯白噪声。

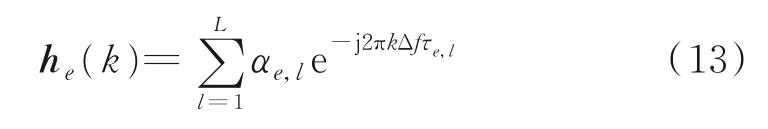
本文所提出的四元数加密算法流程如图7所示。

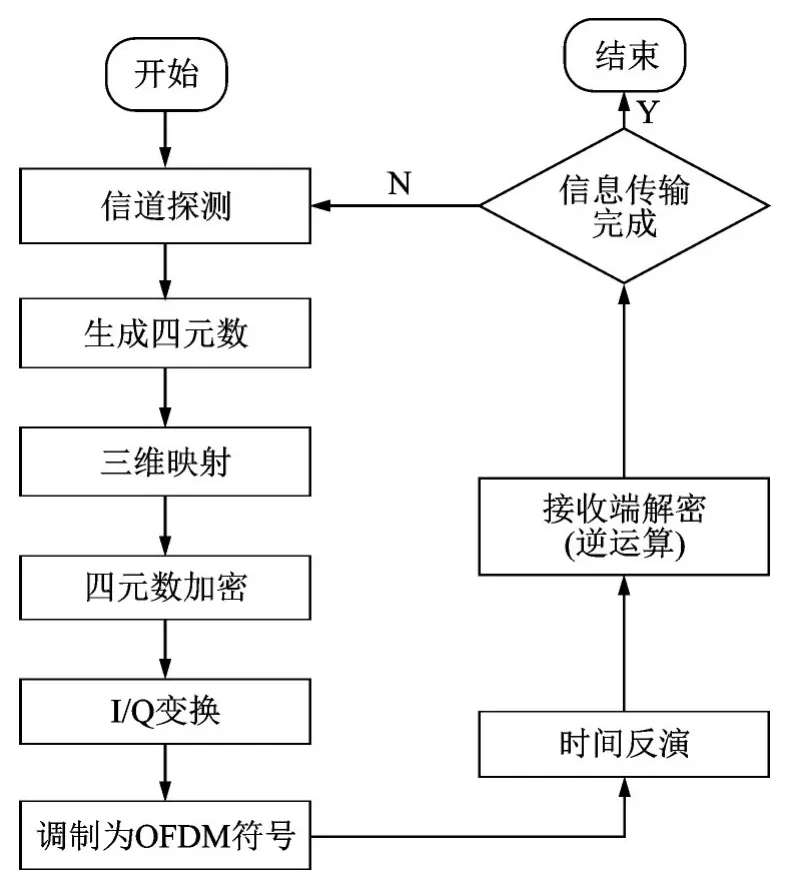
图7 四元数加密算法Fig.7 Quaternion encryption algorithm

3 实验仿真

3.1 MED对比

最小欧氏距离是衡量星座好坏的一个重要标准，在信号能量相等的条件下，二维星座图和三维星座图的MED参数如表1所示。

表1中三维信号星座和二维信号星座的对应关系为：4⁃ary⇌QPSK，16⁃ary⇌16QAM，64⁃ary⇌64QAM，128⁃ary⇌128QAM。从 表1的MED可以看出在信号能量相等的条件下三维星座图的MED基本上优于二维星座图的MED，尤其对于高阶调制信号，增加比尤其明显。

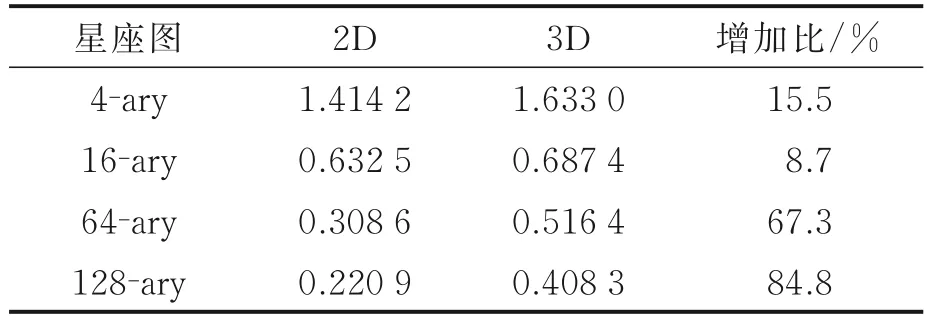
表1 最小欧式距离Table 1 MED

3.2 实验仿真

本节对三维星座点的四元数加密的算法利用MATLAB进行了仿真，设一帧为6个OFDM符号，每个OFDM符号有128个子载波，循环前缀为32，信道为均值为0，方差为1的瑞利多径信道，信道的多径长度为9，蒙特卡洛次数为10 000。

3.2.1 误符号率对比

从图8可见，三维星座信号的误符号率性能相较于二维星座信号都有较大的提升，对于4⁃ary的信号三维相较于二维在误符号率为10-6时提升了约2.5个信噪比，而对于16⁃ary三维星座信号也提升了约2个信噪比。三维星座信号改善误符号率性能基本上与表1中MED的增加比相符。

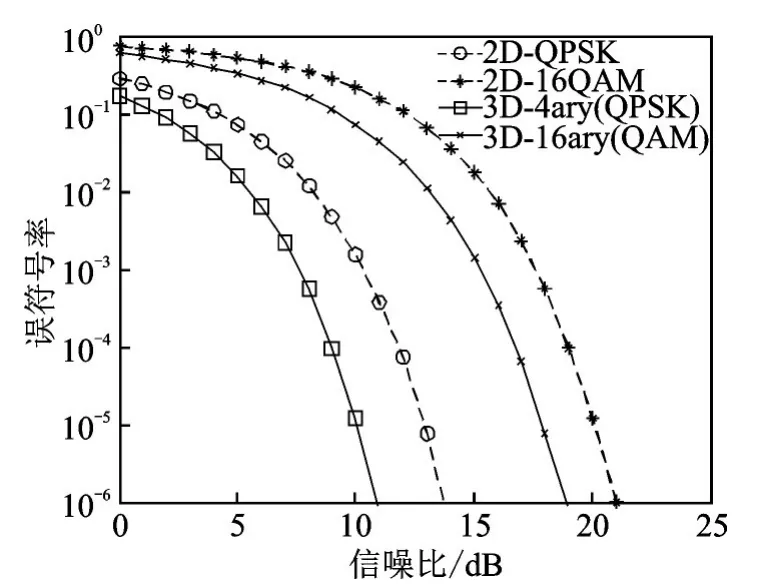
图8 三维星座信号与传统二维星座信号误符号率对比图Fig.8 Comparison of symbol error rate be⁃tween 3D constellation signal and tradi⁃tional 2D constellation signal

3.2.2 误符号率降低比

为了对比二维星座点和三维星座点在相同信噪比下的误符号率性能，本文定义了一个误符号率降低比η

式中：e3D为三维星座点对应的误符号率，e2D为二维星座点对应的误符号率。

从图9可知，随着信噪比的增大，误符号率降低比也逐渐增大。4⁃ary的三维星座点对比于QPSK，当信噪比为12 d B时，误符号率降低比到达下界，而16⁃ary的三维星座点对比于16QAM，当信噪比为20 d B时，误符号率降低比到达下界。并且4⁃ary误符号率降低比明显比16⁃ary的误符号率降低比下降的快。与表1中4⁃ary和16⁃ary的MED增加比相对应。

图9 误符号率降低比Fig.9 Symbol error rate reduction ratio

3.2.3 误符号率

本文所采用的四元数加密算法和文献［15］的人工噪声（Artificial noise，AN）方案误符号率对比如图10所示，随着人工噪声的能量比例增大，窃听者的误符号率明显增大，但同时合法用户的误符号率也会受到损害。且当人工噪声的能量比例为90%时，尽管窃听者的误符号率也保持在较高的水平，但仍低于本文所提的方案。而合法用户的误符号率却受到了较大的影响。

图10 人工噪声方案和本文算法的误符号率性能对比Fig.10 Comparison of symbol error rate perfor⁃mance of the artificial noise scheme and the proposed algorithm

3.2.4 保密传输速率

根据文献［16］对于二进制广播信道的保密传输速率为Cs=H(eAE)-H(eAB)=

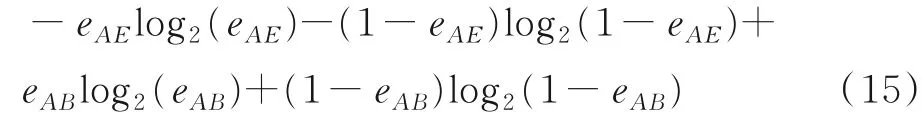
式中：eAB为合法用户Bob的误符号率，eAE为窃听用户Eve的误符号率。本文对4⁃ary的三维星座点和16⁃ary的三维星座点所对应的保密传输速率进行了仿真。仿真结果如图11所示。

从图11可知，文献［15］的人工噪声方案的人工噪声能量比例较小时，其归一化保密传输速率随着信噪比增大，逐渐减小，但是当人工噪声的比例为90%时，人工噪声方案的归一化保密传输速率也开始上升，但由于人工噪声能量比例过高，对合法用户的误符号率也有一定的损害，故其归一化保密传输速率依旧低于本文所提算法。

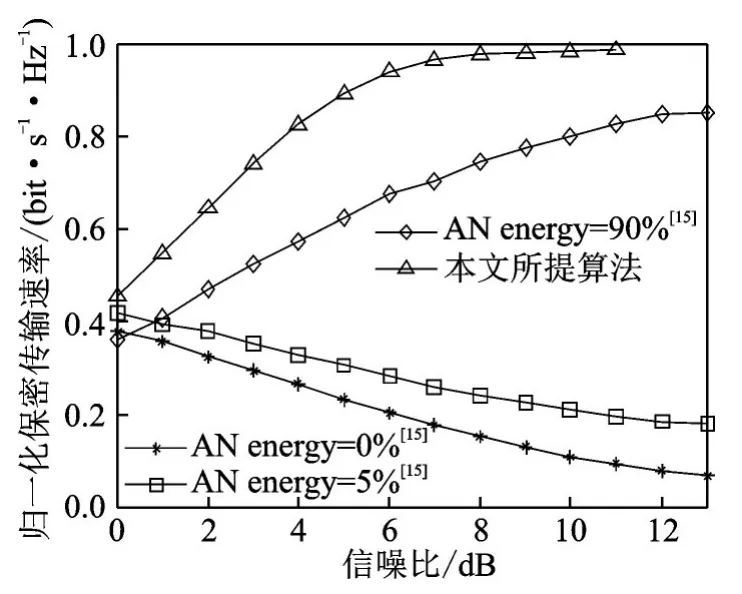
图11 保密传输速率和人工噪声方案归一化保密传输速率对比Fig.11 Comparison of secret transmission rate and the normalized secret transmission rate of the artificial noise scheme

4 结束语

为了保障TR⁃OFDM系统的物理层安全传输，本文提出一种四元数加密算法，首先对TR⁃OFDM的系统模型进行了描述，其次在该模型下，对本文的四元数加密算法步骤进行了详细的说明，最后对四元数加密算法的误符号率和保密传输速率进行了仿真，并与传统的二维星座误符号率进行了对比。通过仿真表明：随着信噪比的增大，本方案可以使窃听者难以获得合法通信双方通信的任何信息，且具有一定的保密传输速率，而合法用户可以获得比传统的二维星座信号更优的误符号率。相较于人工噪声方案，本文所提算法不会影响合法用户的误符号率，这对于提高数据传输速率具有重要的意义，在下一代通信或者军事安全通信中具有重大的潜力。