大规模MIMO通信中基于Jacobi预迭代的改进Gauss⁃Seide算法

史传胜，冯 姣，司 闯，张 锐

（南京信息工程大学电子与信息工程学院，南京 210044）

引 言

大规模MIMO（Massive MIMO）系统已经成为实现5G的一项关键技术，它可以满足5G在高数据传输速率、稳定连接和低延迟等各方面的需求［1］。massive MIMO系统指在基站端配置多达几十乃至数百根天线阵列同时为多个单一天线客户端服务，大大提高了系统的存储空间和自由度，同时还可以改善和提高数据传输速率、链路可靠性以及网络通信容量［2］。在massive MIMO系统中，复杂程度和天线数量是密切相关的，随着天线数量增加，算法的复杂程度随着变高。所以，在接收端需要一种复杂程度低、检测性能高的信号检测算法。

为了提高MIMO系统的信号检测性能，学者们提出了多种检测算法，包括线性检测算法与非线性检测算法等。最大似然估计（Maximum likelihood，ML）算法被认为是一个比较经典的最优检测算法，其遍历性能够保证算法获得最佳检测性能［3］，但由于其复杂度太高，学者们提出了复杂度低的近似线性最佳检测算法，如迫零（Zero forcing，ZF）算法、最小均方误差（Minimum mean square error，MMSE）检测算法［4］。MMSE和ZF涉及矩阵的求逆问题，当用户数量很大时，这些检测器的复杂度会变得很高。基于此，出现了简化算法，如共轭梯度［5］（Conjugate gradient，CG）、高斯‑赛德尔（Gauss‑Seide，GS）［6］、雅克比［7］（Jacobi，JA）、超松弛迭代［8］（Successsive over‑relaxation，SOR）。其中JA收敛速度最慢，但更容易实现。GS是JA的一种改进，精度比JA高，其复杂度和JA差不多。文献［9］提出一种基于雅可比‑理查森联合算法，其基本原理是先利用雅克比迭代算法迭代一次，然后利用雅克比迭代的结果作为RI的初始解。虽然该算法在性能上有所提高，但是其收敛速度较慢。文献［10］提出了一种加入基于雅克比迭代的高斯‑赛德尔（Jacobi gauss‑seide，JA‑GS）方法。JA‑GS算法主要利用雅克比迭代算法和高斯‑赛德尔迭代算法进行信号检测，虽然性能较为接近MMSE，但是收敛速度偏慢，复杂度偏高。

为解决这一问题，本文通过对GS算法进行线性变换，提出了一种适用于大规模MIMO上行链路系统检测算法。该算法通过引入JA预处理器和设计了改进后的高斯‑赛德尔（Improved Gauss‑Seide，IGS）方案，进一步提高了算法的收敛速度和检测性能。仿真结果表明，在64个基站天线和16个用户天线数的前提下，所提算法检测性能优于传统的GS迭代方法和JA‑GS方法。

1 大规模MIMO系统模型

为了简化分析过程，用户设备为单天线的单小区大规模MIMO上行链路系统模型。假设基站接收天线数量为M根，用户传输天线数量为N个［11］。通常有M≫N，例如M=64和N=16。系统原型如图1所示。其中，发射端信号xm经过用户天线N向基站天线传输，基站端天线M接收到的信号经过解调后得到ym。

图1 大规模MIMO系统模型Fig.1 Massive MIMO system model

基站接收的上行信号为

式中：hm表示用户n到基站端的信道列矢量，信道矩阵H=[h1，h2，h3，…，hm，…，hN，]T，维度为M×N；x=[x1，x2，x3，…，xm，…，xN]T为发射信号向量，xm为第m个用户的传输符号，ym代表接收端第m根天线接收的接收信号。在本文中zm是服从均值为0，协方差矩阵为σ2z I的高斯分布。本文假设传输信号{xm}是平均能量归一化的发射向量。

为避免复数运算，将模型转换为等效的实值模型为［12］

2 信号检测算法

2.1 MMSE检测算法

在massive MIMO系统模型中，MMSE检测算法检测性能较为优异，即通过简单的线性操作就可将发送信号x从接收端接收到的信号y中恢复出来。为了恢复发送的信号，使用加权滤波矩阵WMMSE来实现信道的逆转［7］。MMSE算法中发送信号的接收估计值可以表示为［13］

式中：I为单位矩阵，HH为H的对称转置矩阵，WMMSE为MMSE检测算法的滤波矩阵，匹配滤波器输出可以表示为yMF=HHy。算法的复杂度主要体现在矩阵的求逆方面。因此在实际的大规模MIMO系统中，MMSE检测算法很少在实际当中应用。大部分massive MIMO低复杂度检测算法的原理就是通过降低求矩阵的逆的复杂度来降低MMSE整体算法的复杂度。

2.2 高斯⁃赛德尔检测算法

线性检测算法如GS等在massive MIMO系统中具有更优异的检测性能，将式（4）写成-1yMF，通过变换可得yMF=̂，这样可以避免矩阵求逆问题，其中A=HHH+

在massive MIMO系统中，当基站天线数远远超过用户天线数量时，信道逐渐趋于正交［14］，MMSE滤波矩阵为对称正定矩阵，且对角占优。因此，可将A分解为

在高斯‑赛德尔检测方法中，信号可以估计为［11］

式中：D、L和U分别为A的对角矩阵、严格下三角矩阵和严格上三角矩阵。

目前我国学者着力探究大学生不合理信念与学生的生理和心理健康之间存在的联系，并获得了丰富的成果。但是针对不合理信念在学科教育层面中的研究明显不足，尤其是像酒店管理这样的潜力学科，在提升人才培养质量方面表现出持续性的疲软现象。

对于高斯‑赛德尔迭代方法，迭代的初始值在收敛过程中很关键。传统的初始值为零向量，虽然简单但远非真正的初始化方案，因此需要一种复杂程度低且性能高的初始化方法。利用矩阵A正定，且对角占优，可由D-1代替A-1，则相比A可以减少滤波矩阵求逆的计算复杂度。根据式（3），初始解可以写成

后续的高斯‑赛德尔迭代遵循式（6）。

2.3 雅克比算法

雅可比迭代是一种求解线性方程组的迭代求解方法。Jacobi迭代算法由于在各常见迭代算法中收敛速度比较慢，相比于GS，JA检测算法更容易实现，但是检测速度没有GS快，雅克比迭代算法的基本原理是通过对滤波矩阵A进行LU分解，每一次的迭代结果都代入下一次迭代中，通过JA算法进行还原后接收信号的估计值为

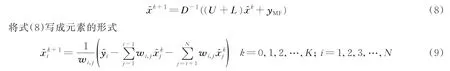
式中：雅克比滤波矩阵为D-1(U+L)；k表示迭代次数。

2.4 基于雅克比预迭代的高斯⁃赛德尔方法

文献［15］利用JA和GS方法设计了一种低复杂度的大规模MIMO上行链路检测器。图2给出了所提出的基于JA预迭代的GS的检测器的一般框图。检测器包括初始化和最终估计两个阶段。JA‑GS的原理是利用雅克比容易实现的特点，将JA迭代的结果作为高斯‑赛德尔的初始值，这样可以提高高斯‑赛德尔的收敛速度和检测性能。当JA‑GS的检测性能接近MMSE的检测性能时，需要迭代4次以上。

图2 基于JA-GS检测器Fig.2 Detector based on JA-GS

将式（7）的结果应用到式（8）中：

3 基于雅克比预迭代的改进高斯⁃赛德尔方法

3.1 带状矩阵

定义1带状矩阵表示在矩阵A中，所有的非零元素都集中在以主对角线为中心上下w元素的带状区域中。其中w小于矩阵的维度。

由A=HHH+σ2I可知，A是一个N×N的方阵。那么带状矩阵Dw可以写成

式中Ai，j为A中的元素。那么式（5）可以写成

式中Lw和Uw为Aw-Dw的严格下三角矩阵和严格上三角矩阵。当w=1时，D1为

3.2 JA⁃IGS算法

JA‑IGS方法主要利用IGS来进行信号检测。将第一次雅克比迭代的值作为整个系统的初始解。改进后的JA‑IGS方法相比于GS和JA‑GS收敛速度更快，检测性能更优异。

通过线性变换，对传统的GS方法做出改进，利用式（12）来更新yMF=A x̂，接收到的信号yMF可以写成

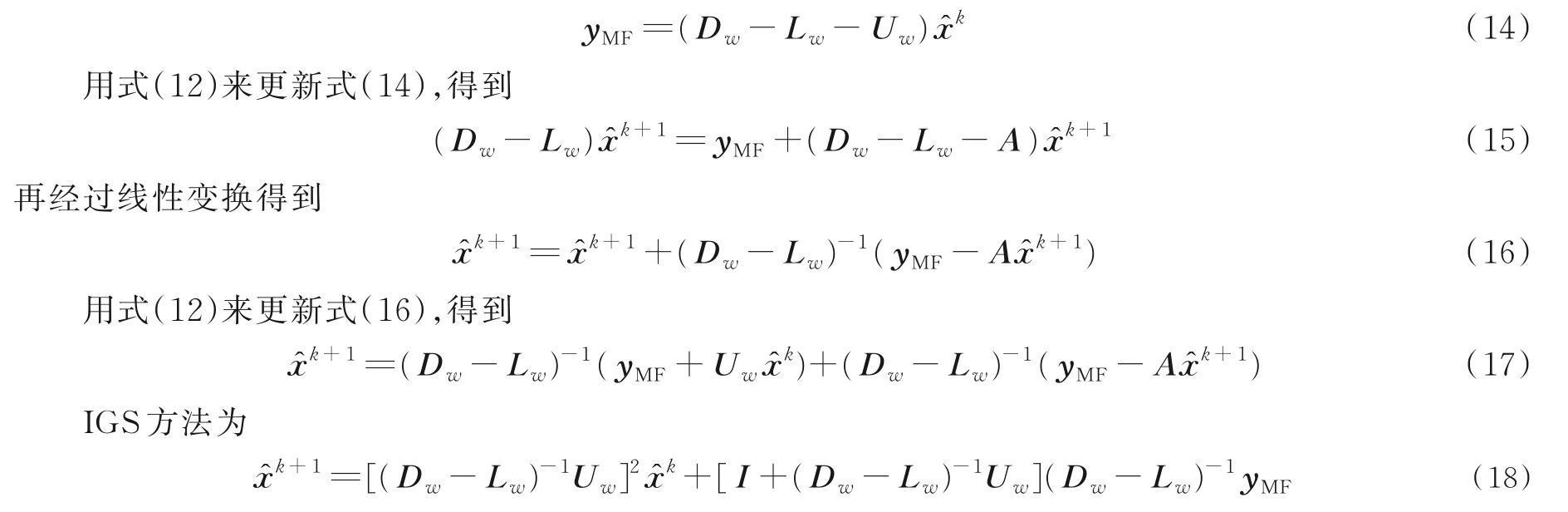
利用雅可比预迭代器来优化IGS迭代的初始解，其中IGS的初始解是x̂1，这样可以提高IGS的收敛速度。

JA‑IGS算法流程图如图3所示。综合上文的描述，所提的JA‑IGS的算法如下。

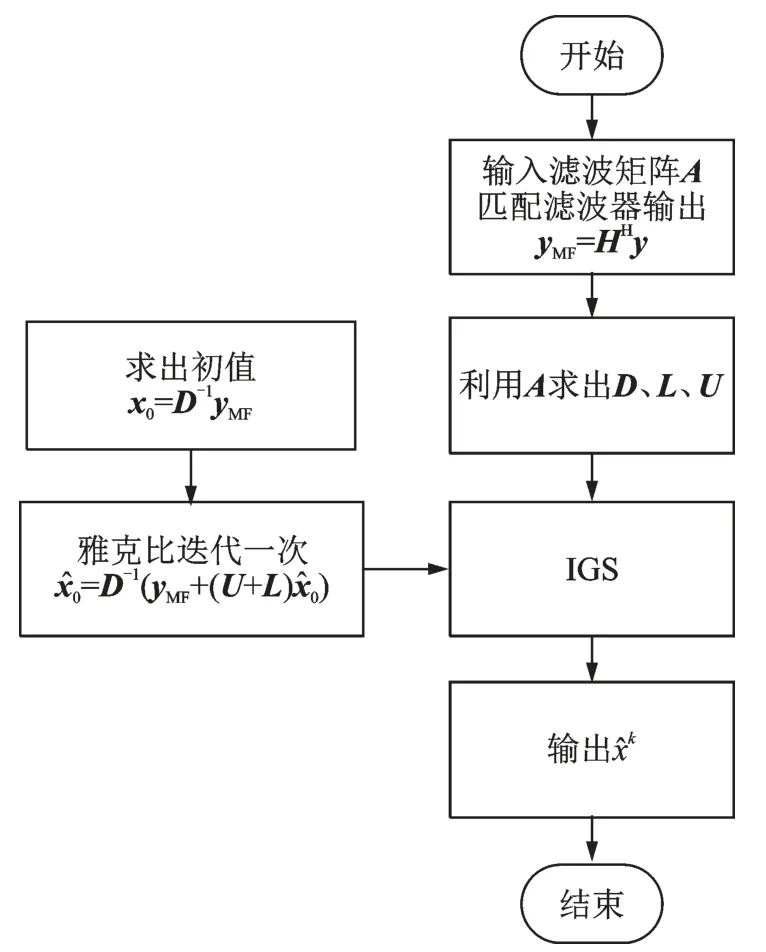
图3 JA-IGS算法流程图Fig.3 JA-IGS algorithm flow chart

算法JA‑IGS检测方法

4 复杂度分析及收敛性分析

4.1 算法复杂度

本文主要比较了JA‑IGS算法的复杂度和一些线性检测算法的复杂度。相比而言，乘法运算的计算复杂度远比加法高［16］，所以算法的复杂度通常是比较乘法运算的次数和相同迭代次数时所需要做的乘法次数。表1列出了JA‑IGS算法、传统的GS、JA和JA‑GS算法的复杂度。其中，N代表用户天线数量，M代表基站天线数量，k代表迭代次数。

表1 不同检测方法计算的复杂度Table 1 Computational complexity of different de⁃tection methods

4.2 收敛性分析

定理如果A是行严格对角占优矩阵，那么高斯‑塞德尔方法的改进对于初始逼近的任意选择都是收敛的。

假设x*为线性系统yMF=̂的实解。因为矩阵A是严格对角占优的矩阵，如果x̂k+1是第k+1次近似解，那么，改进高斯‑赛德尔算法的收敛性可以表示为

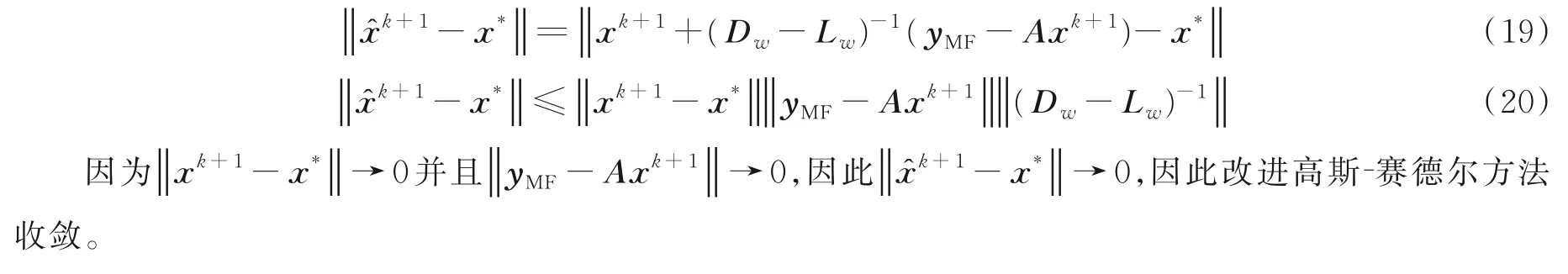
5 性能仿真

为测试算法的检测性能，本文在MATLAB平台上仿真了JA‑IGS和现有算法的误码率（Bit error rate，BER）‑信噪比（Signal noise rate，SNR）曲线。本文分析了所提出的JA‑IGS算法的检测性能并和GS算法和JA‑GS算法以及MMSE的检测性能作了对比。设置仿真时的传输信道为不相关瑞利衰落信道，基带信号调制方式为BPSK、QPSK、QAM，天线规模为64×16。模拟参数如表2所示。

表2 模拟参数Table 2 Simulation parameters

图4对比了不同算法在SNR=12 dB时的计算复杂度，可以看出JA算法的复杂程度最低。JA和GS都是迭代3次且复杂度基本相同，为了平衡检测性能与计算复杂度之间的矛盾，本文提到的JA‑IGS算法的复杂度要比GS和JA‑GS的复杂度稍微高一点。MMSE的复杂度最高，由于MMSE需要矩阵求逆运算，因此MMSE的复杂度最高。

图4 天线数量与算法计算复杂度的关系Fig.4 Relationship between the number of antennas and the computational complexity of the algorithm

表3对比了不同算法在SNR=12 d B时，每比特实乘运算次数。可以看出，MMSE的每比特实乘次数最高、其次是JA‑IGS、JA‑GS、GS、JA。表4对比了JA‑IGS算法在不同用户天线数下的复杂度。在基站天线数量不变的前提下，随着用户数量不断增加，JA‑IGS算法的复杂度不断升高。

表3 SNR=12 dB时，不同算法在64×16天线数量前提下的每比特实乘次数Table 3 Actual multiplication times per bit under the premise of 64×16 antennas for different algorithms when SNR=12 d B

表4 在SNR=12 dB时，不同用户天线数JA⁃IGS算法的实乘次数Table 4 Actual multiplication times of the JA⁃IGS algorithm for different user antenna numbers when SNR=12 dB

图5展示了massive MIMO系统规模为64×16，在64QAM调制下，所提算法的检测性能比较。其中GS、JA、JA‑GS都是迭代3次，JA‑IGS迭代次数分别为k=1和k=2，其中k是迭代次数。根据仿真结果表明，JA‑IGS算法随着迭代次数的增加，算法的检测性能也在不断提高。以GS算法BER曲线作为对比参照，由图5可知，迭代次数为1时，JA‑IGS算法的性能和GS算法的性能相比，传统的GS算法性能更优。当迭代2次时，本文提出的JA‑IGS算法的检测性能比迭代3次的JA、GS和JA‑GS检测性能有明显的优势，在BER=10-3时，相比于GS和JA‑GS，分别有2 d B和0.9 dB的优势，在BER=10-4时，相比于JA‑GS有2 dB的增益。JA‑IGS利用了改进后的高斯‑赛德尔算法，它的收敛速度和检测性能是更优于JA、GS和JA‑GS检测算法。虽然JA‑IGS算法检测性能较好，但是JA‑IGS算法的复杂度是要比JA、GS和JA‑GS要高。

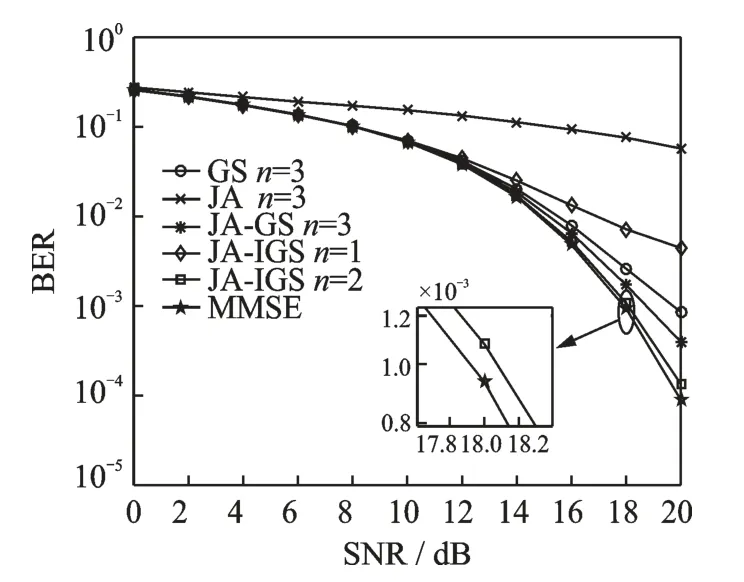
图5 JA-IGS算法误码率性能比较（64×16）Fig.5 Comparison of BER performance of proposed JAIGS algorithm（64×16）

图6展示了massive MIMO系统规模为128×16，在64QAM调制下，所提算法的检测性能比较。可以看出，MMSE算法的性能最好，其次是迭代2次的JA‑IGS算法，最差的是JA算法。迭代3次的JA‑IGS算法和MMSE算法的性能较为接近图7展示了所提JA‑IGS算法在不同基站天线数、16个用户天线数和64QAM调制方式下，且迭代次数都是2时的检测性能比较。由图7可知，在用户天线数量都是16的前提下，随着基站天线数量增加，JA‑IGS算法的检测性能也随之提高。当SNR=16 d B时，在128×16的天线配置下，误码率达到10-5量级，相比之下，SNR=16 dB时，在64×16的天线配置下，误码率只有10-3量级，在32×16的天线配置下，误码率只有10-2量级，天线配置为16×16的BER只有10-1量级。由于基站天线数量变多，空间自由度也随之提高，并且提高信号的传输效率和系统容量。

图6 JA-IGS算法误码率性能比较（128×16）Fig.6 Comparison of BER performance of proposed JA-IGS algorithm（128×16）

图7 不同基站天线数，JA-IGS算法的误码率性能比较Fig.7 Comparison of BER performance of proposed JAIGS algorithm with different numbers of base sta‑tion antenna

图8展示了在64个基站天线、16个用户的配置下，不同调制方式对JA‑IGS算法检测性能的影响。仿真结果表明，该算法在BPSK调制下性能表现更优异，其他性能表现依次是QPSK，16QAM，64QAM。在抗加性高斯白噪声方面BPSK性能最好。由于64QAM调制方法的判决，取样点比BPSK、QPSK、16QAM都要多，所以增大了其误码率，导致它性能最差。

图8 BPSK、QPSK、16QAM和64QAM调制下的JA-IGS性能比较Fig.8 Comparison of BER performance of proposed JA-IGS algorithm with different modulation schemes (BPSK, QPSK, 16QAM and 64QAM)

6 结束语

本文提出了一种新的大规模多输入多输出系统的上行链路用户信号检测算法。为了提高算法的收敛速度，本文采用具有更快收敛速度的JA‑IGS迭代算法。该方法通过改进传统的GS迭代方法，且引入JA迭代作为IGS的初始值，仿真结果表明，JA‑IGS算法获得了较优的误码率性能，和传统的大规模多输入多输出检测算法相比有明显的的优势。随着基站天线数量的增加，该算法的性能得到改善，随着调制阶数的增加，性能也随之下降。