一类计算M-矩阵逆的二次收敛算法

关晋瑞，任孚鲛

(太原师范学院 数学系，山西 晋中 030619)

1 引言

M-矩阵的概念是Ostrowski在1937年提出的.作为一类重要的特殊矩阵，M-矩阵的应用十分广泛，它在科学计算和工程应用的许多领域，如矩阵理论、微分方程数值解、线性方程组迭代求解、线性互补问题、Markov链等问题中都有着重要的应用[1-4].此外，M-矩阵在其他学科如物理学、生物学，以及经济学中也有着广泛的应用.

由于M-矩阵广泛的应用和优美的性质，国内外很多人对其进行了深入的研究，得到了众多的成果.自M-矩阵的概念提出之后，其众多的性质和等价条件不断被发现，在专著[1]中总结的非奇异M-矩阵的等价条件已有50多个，之后还在继续扩充[5-7].特别地，对于M-矩阵的判别也是人们一直探讨的一个问题[8-9].

本文研究M-矩阵的逆矩阵的计算问题.一般求逆矩阵的算法是基于列主元高斯消去法得到的，但是用来计算M-矩阵的逆时，存在一定的缺陷：一方面，一般的算法未能充分利用M-矩阵丰富的性质和结构；另一方面，当矩阵接近奇异时，所求出的逆矩阵可能误差比较大.为了有效地计算M-矩阵的逆，本文提出了一类迭代法，该方法充分利用了M-矩阵的特点，在迭代中保持非负性，且具有二次收敛速度.

本文内容安排如下：第2节给出本文所需的一些预备知识.第3节，提出一类计算M-矩阵逆的迭代算法，并分析其收敛性.第4节，给出几个数值例子以验证新方法的可行性和有效性.最后是简要的总结.

2 预备知识

本节介绍文中的符号记法、M-矩阵的定义和若干基本性质，以及后面将要用到的一些预备知识.

我们用Rm×n表示实数域上全体m×n的矩阵，用Rn表示实数域上全体n维列向量，用ρ(A)表示矩阵A的谱半径.n阶单位矩阵记为In，在没有混淆的情况下写为I.用‖·‖来表示一个给定的矩阵范数.

设A=(aij)∈Rn×n，若对于任意的i≠j都有aij≤0成立，则称A为Z-矩阵.对于Z-矩阵A，若存在非负矩阵B使得A=sI-B且s≥ρ(B)成立，则称该Z-矩阵为M-矩阵，其中ρ(B)表示矩阵B的谱半径.特别地，若s>ρ(B)，则称A为非奇异的M-矩阵，若s=ρ(B)则称A为奇异的M-矩阵.

引理2.1[1]设A∈Rn×n为Z-矩阵，则下面几个结论是等价的：

1)A是非奇异的M-矩阵；

2)A-1≥0；

3)存在正向量v>0，使得Av>0；

4)A的全部特征值都具有正实部.

引理2.2[1]设A，B为非奇异的M-矩阵，且A≤B，则有A-1≥B-1.

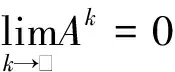
3 一类二次收敛算法

本节中，利用M-矩阵的特点提出一类迭代法来计算它的逆，并给出新方法的收敛性分析.

设A∈Rn×n为非奇异的M-矩阵，则A可表示为A=sI-B，其中B为非负矩阵且s>ρ(B).矩阵A的逆A-1满足下面的矩阵方程

AX=I.

将A=sI-B代入上式，整理可得如下不动点格式

从而可得迭代法

(3.1)

该迭代法在每步计算中，主要运算为一个矩阵乘积，运算量大约为2n3.

以下分析迭代法(3.1)的收敛性结果.

引理3.1 设A∈Rn×n为非奇异的M-矩阵，则对任意的k≥0，由迭代法(3.1)生成的序列{Xk}满足下式

0≤Xk≤Xk+1≤A-1.

(3.2)

证明：利用数学归纳法来证明(3.2).

根据引理2.2可得X1≤A-1.于是当k=0时结论(3.2)成立.

假设当k=l时结论成立，则由

可知

因此结论对于k=l+1也成立.

根据数学归纳法，结论(3.2)对任意的k≥0都成立.证毕.

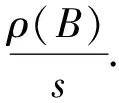
从引理3.1证明中可知

B1=s1I-s2I+B2，

从而ρ(B1)=s1-s2+ρ(B2).于是

为了提高迭代法(3.1)收敛率，利用矩阵技巧，我们将其迭代格式改写为如下形式

(3.3)

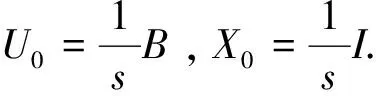
定理3.3 设A∈Rn×n为非奇异的M-矩阵，则由迭代法(3.3)生成的序列{Xk}具有二次收敛率.

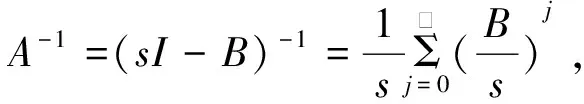
于是

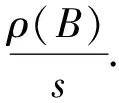
4 数值算例

例4.1 考虑n阶非奇异M-矩阵

对于阶数的不同取值，实验结果见表4.1.

表4.1 例4.1的实验结果

例4.2 在Matlab中按照如下命令随机生成n阶的非奇异M-矩阵

a=rand(n，n)；A=diag(a*ones(n，1))-a+eye(n)；

对于阶数n的不同取值，实验结果见表4.2.

表4.2 例4.2的实验结果

例4.3 考虑非奇异M-矩阵

其中ε>0.当ε→0时，矩阵A接近奇异.对于参数ε的不同取值，实验结果见表4.3.

表4.3 例4.3的实验结果

由上述三个例子可见，算法(3.3)是可行的，而且也是较为有效的.

结论

本文研究了M-矩阵逆的迭代算法，并提出了一类二次收敛的算法以计算非奇异M-矩阵的逆矩阵，并证明了相应的收敛性分析.数值例子表明，新方法是可行的，而且在一定情况下也是较为有效的.