超贝叶斯图模型及其联结树的构建
2021-12-20甘亚男耿生玲
甘亚男,耿生玲,2*,郝 立
(1.青海师范大学 计算机学院,青海 西宁 810008;2.高原科学与可持续发展研究院,青海 西宁 810008)
0 引言
在现实世界里,确定性事物是相对的,不确定性事物是绝对的.各行各业的飞速发展,使得我们步入了大数据的时代,这意味着会有海量的数据持续输出,这些数据中包含大量的不确定性数据[1],如何处理这些不确定性数据?是我们所面临的严峻问题.基于此引入贝叶斯网络来解决,贝叶斯网络[2,3],它是一种概率图型模型[4,5],早在1990年Pearl就提出概率图模型(Probability Graph Model,PGM),概率图模型是一种用图论的方式来表示变量间的概率依赖性的模型[6],Pearl[7]认为一个有向无环图,只有在满足条件独立性并具有概率语义的情况下才能被称作为一个概率图模型.贝叶斯网的概率图模型是不确定性知识表示和推理的有效架构.
但由于数据规模的越来越大,关系越来越复杂,一般的贝叶斯网就显得无能为力了,此时超图理论得天独厚的优势就显现出来了.超图的概念是在图论的基础上扩展得来的.图论是起源于七桥问题,在1736年,瑞典的数学家欧拉(Euler)[8,9]把七桥问题转换成图的形式得以解决,轰动一时,图论就由此诞生了.超图[10-14]是有限集的子集系统,是最普遍的离散结构,能够描述复杂的关系和结构.由于超图理论较抽象和复杂,起初的研究和应用进展较为缓慢,但近年来在数学、计算机科学、工程技术、通信、经济学、电信、物理学、运行管理、计算生物学、生物化学和分子生物学等各个领域,对超图理论的研究越来越多,应用越来越广泛.
本文将贝叶斯网与超图结合提出一个新模型-超贝叶斯图模型,用来表示复杂数据间的相关性以及数据间不确定性的表示.分析了超贝叶斯图的条件独立性的性质,从而给出超贝叶斯图的联结树的构建方法及算法,基于联结树不仅可以表示复杂数据间的依赖结构,还可进行概率化简.为超贝叶斯图描述和处理不确定性数据提供了理论依据.经过理论证明和实例仿真该超贝叶斯图是一种有效的不确定性模型.在超贝叶斯网的基础上定义了超贝叶斯图与超贝叶斯图的联结树.
1 基本概念
定义1[15]一个贝叶斯网是一个二元组S=(G,Θ),其中
(1)G是有向无环图;
(2)Θ={P(Xi|pa(Xi))|1≤i≤n}是量化网络的一组变量,表示每个节点Xi在给定其父节点集pa(Xi)下的条件概率分布.
定义2[16]设R为离散变量的有限集,p(R)为联合概率分布(jpd),X、Y、Z是R的三个不相交子集,如果满足:
p(X|Y,Z)=p(X,Z)或者
(1)
(2)
则称为X,Y是关于Z条件独立(简称CI),记为I(X,Z,Y).
事实上,贝叶斯网络是以图形化的方式表示变量间的依赖关系和条件独立关系.条件独立关系根据覆盖程度可分为非嵌入式条件独立和嵌入式条件独立.即若事件X,Y关于事件Z条件独立:
(1)如果R=XYZ,则把I(X,Z,Y)的集合为非嵌入式条件独立集合(简称UCI).
(2)如果XYZ⊂R,并且不存在另一个I(X′,Z,Y′),其中X′⊂X或者Y′⊂Y,则I(X,Z,Y)的集合为嵌入式条件独立集合(简称ECI).
定义3[11]超图表示为H=(V,HE),其中:
(1)V是H的顶点集;
(2)HE={ei≠Ø|e⊆D}是H的超边集.
在实际应用中,由于不确定性数据规模的越来越大,关系越来越复杂,一般的贝叶斯网就显得无能为力.本文结合超图给出超贝叶斯网,用来表示复杂的不确定性数据依赖关系.
2 超贝叶斯图及其联结树
给定一个有向无环图可生成一个超贝叶斯图.假设一个有向无环图D=(V,E),节点集为V={ai|i=1,2,…,n},边集为E={ei|i=1,2,…,m},pa(ai)为节点ai的父节点.
定义4 一个超贝叶斯图定义为HD=(G,Θ),其中
(1)G=(D,HE={ei=〈ai,pa(ai)〉|i=1,2,…,t,ai∈D})是一个超图;
(2)Θ={P(ei)}是量化网络的一组变量,表示每个超边ei的条件概率分布.
定理1 一个有向无环图,它的超贝叶斯图是唯一的.
证明:根据定义4即可得证.
下面给出超贝叶斯图的键的概念,再讨论超贝叶斯图的结构和条件独立性的性质.
定义5 令超贝叶斯图HD=(D,HE),HE={h1,h2,…,ht},X,Y⊂D,若∀I(X,Z,Y)都满足以下条件:
(1)Z⊂h,其中h∈HE;
(2)I{XZ1,Z2,Y)∉UCI(HD),其中Z=Z1Z2,Z1≠Ø,Z2≠Ø.
则称Z为超贝叶斯图的键.
根据定义,Z必须是超贝叶斯图的某条超边h∈HD的子集.设节点ai,并且它的双亲pa(ai)={b1,b2,…,bm},这就意味着超贝叶斯图的键有以下四种类别,如图1所示.

图1 超贝叶斯图的键
(1)Z=ai,节点ai本身作为超贝叶斯图的键;
(2)Z=pa(ai),节点ai的父节点pa(ai)作为超贝叶斯图的键;
(3)Z=pa′(ai)⊂pa(ai),节点ai的父节点pa(ai)或父节点pa(ai)的子集pa′(ai)作为超贝叶斯图的键;
(4)Z=aiYpa′(ai),节点ai和其父节点的子集pa′(ai)一同作为超贝叶斯图的键.
由此可知,超贝叶斯图的同一个键对于不同的超边可以属于不同的类别,并且一个超边可以包含多个超贝叶斯图的键.
由定义4和定义5讨论超贝叶斯图的键的独立集合的性质.
定理2 设LI(HD)为超贝叶斯图HD的键的独立集合,则LI(HD)⊂UCI(HD).
证明:UCI(HD)表示在超贝叶斯图上所以满足条件独立的集合,LI(HD)表示超贝叶斯图的键,根据定义5第一个条件Z⊂h,其中h∈HE,可知Z一定是超贝叶斯图的一个超边的子集,而UCI(HD)却没做任何限制,则LI(HD)⊂UCI(HD),证毕.
定理3 超贝叶斯图的键的独立集合设LI(HD)是唯一的.
证明:根据定义5即可得证.
定理4 对于∀I(X,Z,Y)∈LI(HD),超贝叶斯图的键Z不能被LI(HD)分割.
证明:根据定义5的第一个条件Z⊂h,其中h∈HD,可知它的贝叶斯超图的键包含在一条超边中,这就意味着它永远不会被LI(HD)分割,证毕.
性质1(对称性)I(X,Z,Y)=I(Y,Z,X).
证明:根据定义5可知在删除节点Z后节点X和Y发生的概率相互不影响,所以I(X,Z,Y)=I(Y,Z,X)成立.
性质2(分解性)I(X,Z,YW)可分解为:I(X,Z,Y)和I(X,Z,W).
证明:根据定义5可知在删除节点Z后,把超贝叶斯图分成X、Y和W三部分,则X、Y和W发生的概率互不影响,所以I(X,Z,YW)可分解为:I(X,Z,Y)和I(X,Z,W).
基于以上的定义和定理,可以给出超贝叶斯图的键的生成算法.
Algorithm1DAG_LI(HD)
Input:a DAG G //有向无环图G
Output:LIs//超贝叶斯图HD的键集LI(HD)
{
Step 1 V=Ø //有向无环图的节点集V
Step 2 BH=Ø. //超贝叶斯的边的集合
Step 3 UCIs=Ø. //非嵌入式条件独立集合
Step 4 LIs=Ø. //超贝叶斯图的键的集合
Step 5 For eachdi∈DAG,i=1,…|DAG|
Step 6 V=V∪di.self;
Step 7 Ifdi.parents≠Ø
Step 8BH=BH∪Set_Generator(di.self,di.parents); //BH由节点di与其父节点组成
Step 9 For eachBHi∈BH,i=1,…,|BH|
Step 10 subset=Subset_Generator(BHi); //生成BH集合的子集
Step 11 For eachbhj∈subset,j=1,…,|subset|
Step 12 z=I_Generator(bhj);
Step 13 If z≠Ø
Step 14 UCIs=UCIs∪z;
Step 15 For eachucii∈UCIs,i=1,…,|UCIs |
Step 16 IfUCI_Filter(ucii)=true
Step 17 LHIs=LHIs∪ucii;
}
分析DAG_LI(HD)算法可知,假设全集D的长度为n,算法在Step 8运行结束最坏的情况下的时间复杂度为O(n),假设超贝叶斯图集合的元素数为m,可知m≤n一定成立,算法在Step 14运行结束时间复杂度为O(m),在Step 17运行结束时间复杂度取决于非嵌入式条件独立集合的长度(即有向无环图的结构),所以在最坏的情况下时间复杂度为O(max(|UCI|)).
假设一个有向无环图D=(V,E),节点集为V={ai|i=1,2,…,n},边集为E={ei|i=1,2,…,m},它的超贝叶斯图HD=(G,Θ).为了进行超贝叶斯图的概率计算与化简,需要给出超贝叶斯图的联结树.
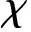
(1)T=(D,HE)是一棵根H0的树,且H0包含超贝叶斯图的所有节点,其中D是超贝叶斯图节点的集合,HE是超贝叶斯图边的集合;

在超贝叶斯图中又在超贝叶斯图的联结树中的边称为简单超边.在超贝叶斯图的联结树中而不在超贝叶斯图中的边称为复杂超边.
超贝叶斯图的联结树可以由超贝叶斯图生成.已知由算法DAG_LI(HD)生成超贝叶斯图的键的集合LI(HD),用超贝叶斯图的键来分割问题域中随机变量集R结果放入一个集合中,判断该集合如果不为空,则把被分割问题域中随机变量集R的左边部分和右边部分的并集存入超贝叶斯图的联结树的边集LH中.下面给出生成超叶斯图的联结树的过程.
Algorithm2LI(HD)_LH
Input:LI(HD)and set R
Output:a set H of Line Hypertree
{
Step 1H=Ø.
Step 2 For eachLIi∈LIs,i=1,…,|LIs|
Step 3 Let result=R_Split_Result(R,LIi);
Step 4 If result≠Ø{
Step 5 H=R_Split(result.left)∪R_Split(result.right);
Step 6 Return H
}
}
分析LI(HD)_LH算法可知,该算法在执行到Step 3时需要遍历整个超贝叶斯图的键的集合LIs,则它的时间复杂度为O(|LIs|);在Step 4用超贝叶斯图的键来分割问题域中随机变量集R时,时间复杂度最坏为O(|R|),根据超定义5超贝叶斯图的键可知|R|>|LIs|一定成立,综上所述算法LI(HD)_LH在最坏的情况下的复杂度为O(|R|).
3 超贝叶斯图的概率分解
根据算法LI(HD)_LH生成的超贝叶斯图的联结树集合以及联合概率分布定义的可知:
(3)
其中hi(i=1,2,…,n)表示LI(HD)_LH算法生成的超贝叶斯图的联结树集合的元素即超贝叶斯图的联结树的每条超边,zj(j=1,2,…,m)表示DAG_LI(HD)算法生成的超贝叶斯图的键.
定义7 令H={h1,h2,…,hn}是一个有超贝叶斯图的联结树,定义hi(i=1,2…,n)的祖先集为:
An(h)={pa(ai)|ai节点在h中}
(4)
定理5 令贝叶斯网的节点集合为R,它的相关有向无环图为D.如果R′∈R是一个祖先集或最小祖先集,那么有:
p(R′)=∏a∈R′p(a|pa(a))
(5)
证明:我们构造一个有向无环图D′,它的节点构成集合R′,有向边(a,b)在D′中当且仅当a,b∈R′,因为R是一组(最小)的祖先集,这表明对于任意节点a∈R′,它的父节点集pa(a)对原本的有向无环图D也是父节点集,即pa(a)⊂R′,因此,对于D′的任意节点a,我们可以将与原始的有向无环图D相关联的联合概率分布p(a|pa(a))附加到D′中的节点a上.则可得到p(R′)=∏a∈R′p(a|pa(a)),证毕.
对超贝叶斯图的概率分解为:
p(hi)=∑An(hi)-hip(An(hi))∏ai∈hip(ai|pa(ai))=∑An(hi)-hi∏x∈An(hi)-hip(x|pa(x))
(6)
以上的累加过程可以可视化为在超贝叶斯图中依次删除节点及其附带的有向边的过程.把每条超边看成一个超贝叶斯图,递归整个过程即可得到最终的分解.
4 算例分析
例1 图2是一个贝叶斯网的经典例子,问题域中包含8个随机变量V、S、T、L、B、C、X、D.即R={V、S、T、L、B、C、X、D}.

图2 贝叶斯图
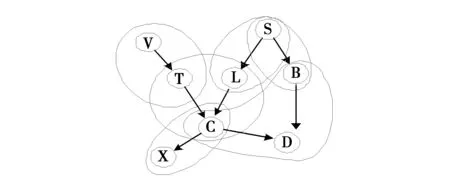
图3 超贝叶斯图
根据定义4超贝叶斯图为:
HD={h1=VT,h2=TCL,h3=SL,h4=SB,h5=CX,h6=BCD}
根据算法DAG_LI(HD)执行过程,则生成的超贝叶斯图的键的集合为:
LI(HD)={I{V,T,SLBCDX},I{VT,C,SLBDX},I{V,TC,SLBDX},I{VT,CL,SBDX},I{V,TL,SBDCX},I{VT,CD,SLBX},I{VT,CB,SLDX}}
={I{V,T,SLBCDX},I{VT,C,SLBDX},I{VT,CB,SLDX}}
={I{V,T,SLBCDX},I{VT,C,SLBDX},I{VTX,C,SLBD},I{X,C,VTSLBD},I{VT,CB,
SLDX},I{VTDX,CB,SL},I{DX,CB,VTSL},I{VTD,CB,SLX},I{VTX,CB,SLD},
I{D,CB,VTSLX},I{X,CB,VTSLB}}
={I{V,T,SLBCDX},I{VT,C,SLBDX},I{VTX,C,SLBD},I{X,C,VTSLBD},I{VTDX,CB,
SL},I{DX,CB,VTSL},I{VTD,CB,SLX},I{D,CB,VTSLX},I{X,CB,VTSLB}}
其中带下划线的表示该元素的位置是不确定的,即I{X,Z,YW}=I{WX,Z,Y}=I{YW,Z,X}=I{Y,Z,WX},在上述过程中我们只取了一种结果,因为无论怎么排列组合对超贝叶斯图的键Z是没有影响的.
R集合为{V、T、S、L、B、C、D、X},根据算法LI(HD)_LH分解集合{VTSLBCDX}过程为:
{VTSLBCDX}={VT}{TSLBCDX}={VT}{CT}{CSLBCDX}={VT}{CT}{CX}{CSLBD}
={VT}{CT}{CX}{CBD}{CBSL}={VT}{CTL}{CX}{CBD}{CBSL}
最终得到超贝叶斯图的联结树为:
H={h1=VT,h2=TCL,h3=CX,h4=CBD,h5=CBSL}

图4 超贝叶斯图的联结树
超贝叶斯图的联结树的联合概率分布为:
根据定理5对超贝叶斯图的联结树的边进行JPD分解为:
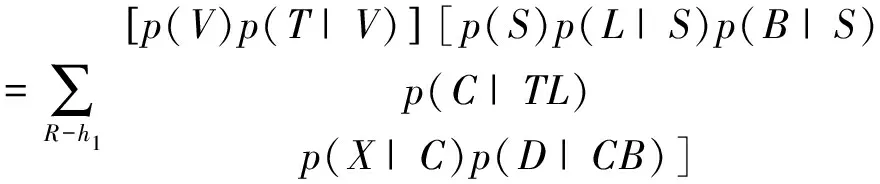

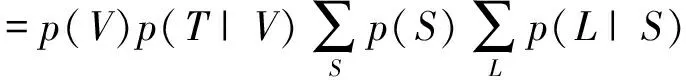
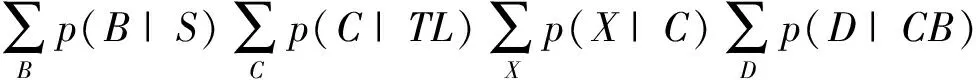
=p(V)p(T|V)
图5中R-h1中变量的上标表示了它们被删除的顺序.注意R-{V,T}中的所有节点都不是h1中任何节点的祖先,依次删除,如对应于上述中的求和序列.还要注意,超边h1是一个简单的超边,c是它所包含的唯一超贝叶斯图的键.删除R-{V,T}中的所有节点后,最终结果如图5所示:

图5 删除过程
同样用定理5对每条边进行分解得到:
p(h1=VT)=p(V)p(T|V)
p(h2=TCL)=p(C|TL)p(L)p(T)
p(h3=XC)=p(X|C)p(C)
p(h4=CBD)=p(D|CB)p(CB)
把每条超边看成一个DAG递归上述过程得到:
p(VT)=p(V)p(T|V)
p(TCL)=p(C|TL)p(L)p(T)
p(XC)=p(X|C)p(C)
p(CBD)=p(D|CB)p(CB)
p(SB)=p(S)p(B|S)
p(SL)=p(S)p(L|S)
5 结束语
本文将贝叶斯网与超图结合定义了超贝叶斯图模型,讨论了超贝叶斯图的条件独立性性质和联结树的构建方法和算法,基于联结树不仅可以表示复杂数据间的依赖结构,还可进行概率化简.为超贝叶斯图描述和处理不确定性数据问题提供了理论依据.基于超贝叶斯图的推理、查询和数据分析等问题还有待探讨.
