双指标L16（45）试验数据分析改进一例

◆俞钟行/ 文

很多DOE（试验设计）专家的著作都只讲单指标的DOE，如Montgomery、Box、田口玄一、任露泉、吴建福等，但在我们的实际工作中经常面临多指标的DOE。而现在介绍多指标DOE文献所采用的方法，基本是在获得单指标最佳参数组合的基础上，根据有关试验的专业知识（如精矿粉造球、注塑成型、焊接工艺等）来做取舍。本文完全根据数据本身的情况，即根据“算法”做出分析和优化的流程，便于用计算机软件实施和标准化。

1.原例介绍[1]

为了提高钢帘线的抗拉强度Y和断面收缩率Z，选择4个因素，每个因素4个水平（见表1），施行中科院推荐正交试验L16（45），试验方案、所得数据与极差分析结果，列于表2。

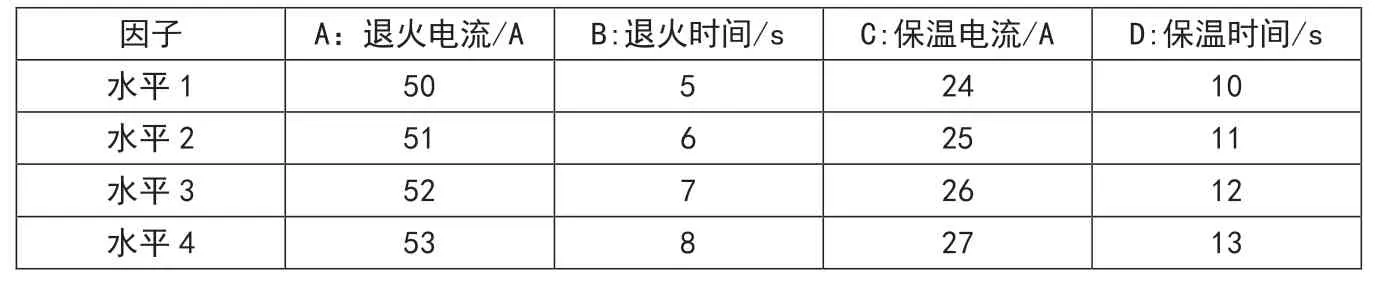
表1 因素水平表

原文献的弱点是缺乏处理多指标DOE数据的手段。它采取的策略是：在抗拉强度大于833MPa的情况下选择各因子水平中断面收缩率最大的结果是A2B4C3D3。实际上就是表2第3次试验的参数组合。原文献选出的最佳参数组合具体为——A：退火电流取51A；B：退火时间取8s；C：保温电流取26A；D：保温时间取12s。做3次试验抗拉强度Y平均值为959.42MPa，断面收缩率Z平均值为65.2%，满足生产要求。

2.用“因素趋势法”[2]分析数据

下面基于excel，用“因素趋势法”来分析上例所得数据。分为3步：⑴画出每个指标的因素趋势图；⑵通过“插项”，用excel的“回归”模块获得每个指标拟合优度高的回归方程；⑶把两个指标各自的回归方程合在一起（即相加），用excel的“规划求解”选优。

⑴先求抗拉强度Y的回归方程，为此，根据表2画出它的因素趋势图（图1）。因素A和C都呈倒V型形状，根据经验判断，它们是“2次项”。Excel上最后界面如表3所示。上述情况在“插项”后通过回归结果都可以看到拟合优度有显著提升，最后的回归结果如图2所示。在“插项”前，Multiple R=0.544515、标准误差=152.0385、Significance F= 0.380225、残差= 254272.7，因素A、B、C和D的P-value= 0.365234、0.427139、0.398818和0.158097。现在仅因素B的P-value较高，但它也正是最弱的因素。得到的回归方程的常数项及各变量系数可从图2下表中Coefficients列读出。抗拉强度Y的回归方程为：

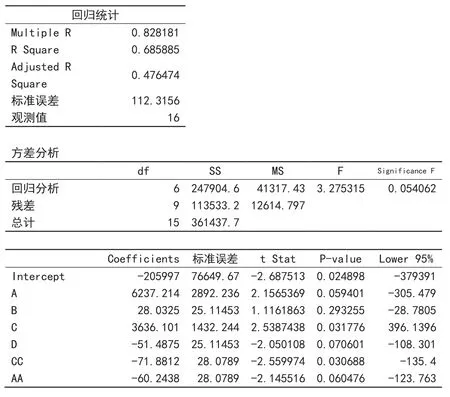
图2 抗拉强度Y的回归分析结果

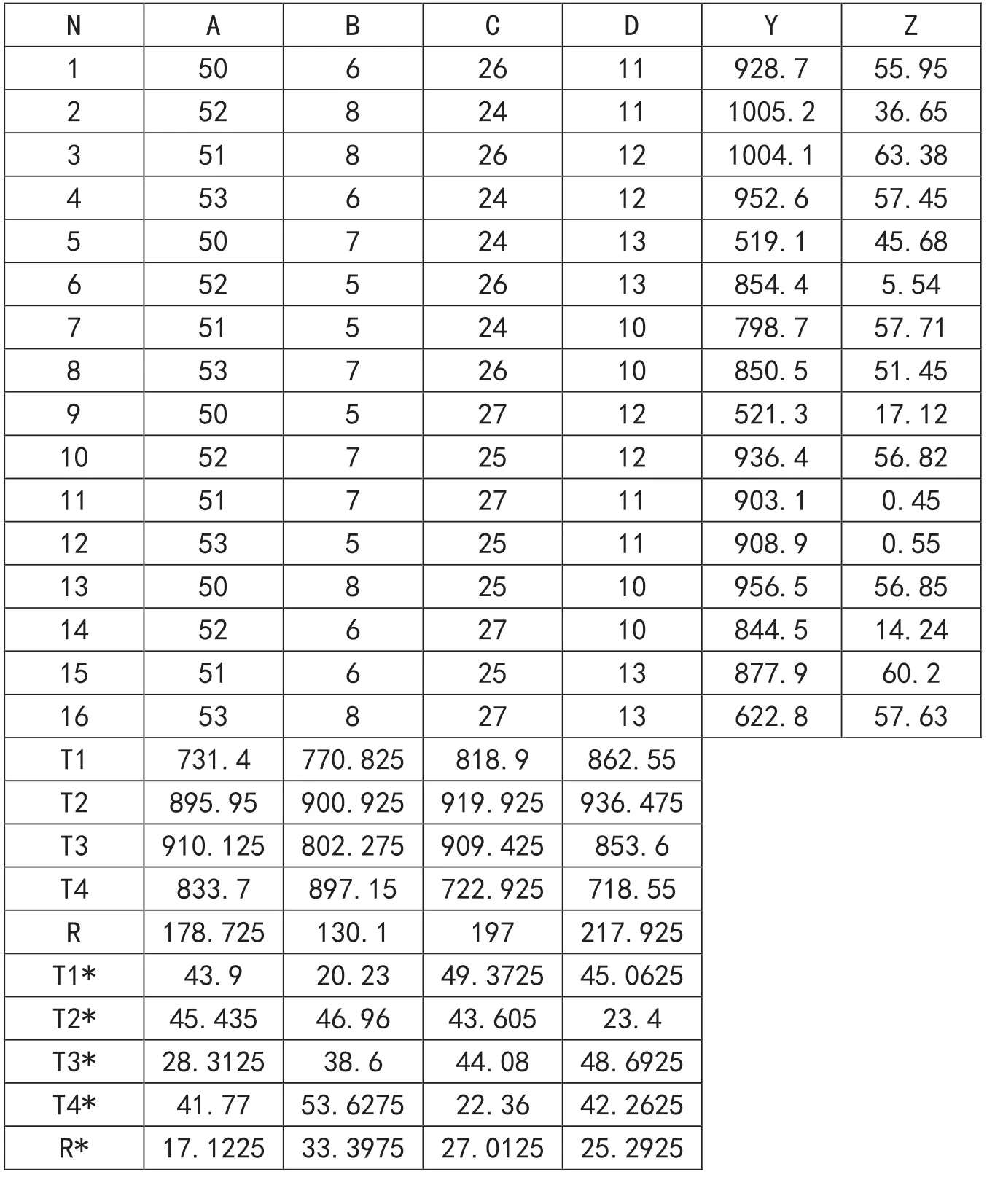
表2 L16（45）试验结果和极差分析

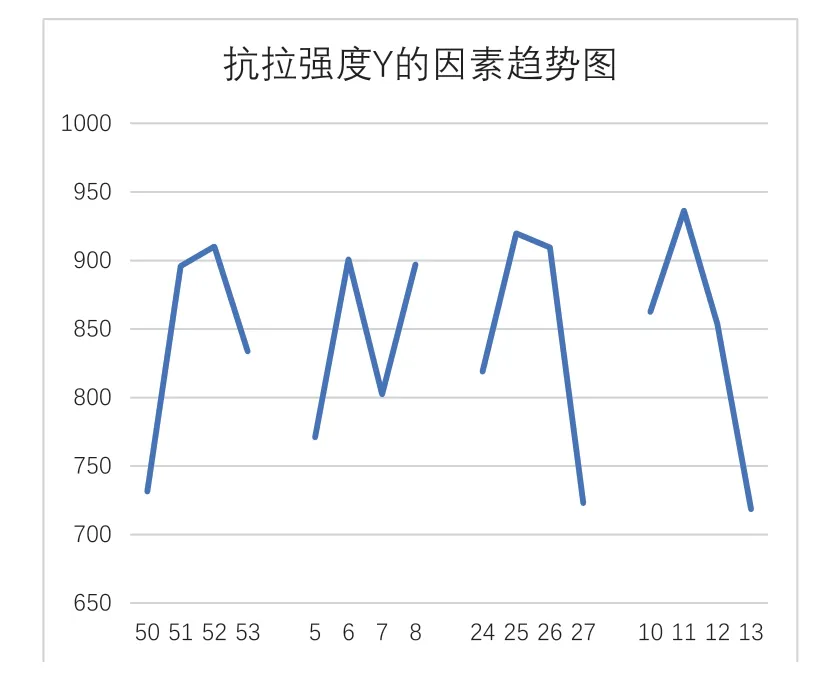
图1 抗拉强度Y的因素趋势图

⑵再求断面收缩率Z的回归方程，为此根据表2画出它的因素趋势图（图3）。因素B和C是最强的两个因素，且变化趋势基本相反，有交互作用，“插项”后回归证实成功。B和A变化趋势相反，有交互作用，“插项”后回归亦证实成功。Excel上最后界面如表3所示。上述情况在“插项”后通过回归结果都可以看到拟合优度有显著提升，D因素的p值太大，删去。最后的回归结果如图4所示。在“插项”前，Multiple R= 0.613544、标准误差=21.7879、Significance F=0.2285811、残差=5221.838，因素A、B、C和D的P-value=0.638832、0.086116、0.126432和0.735335。得到的回归方程的常数项及各变量系数可从图4下表中Coefficients列读出。断面收缩率Z的回归方程为：

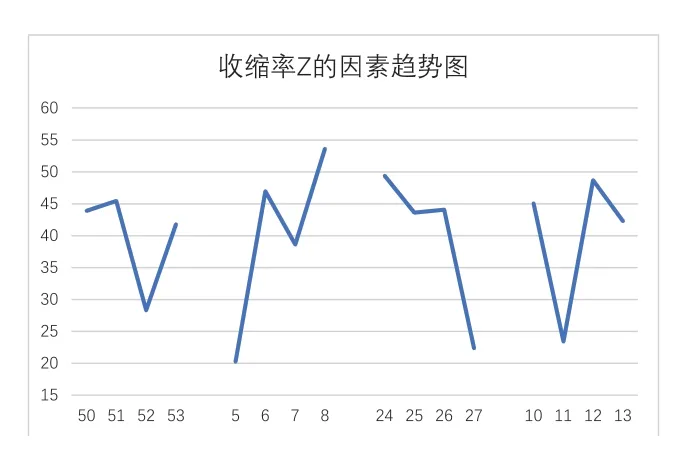
图3 收缩率Z的因素趋势图

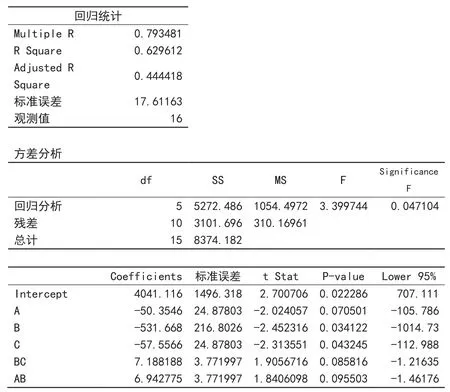
图4 收缩率Z的回归分析结果

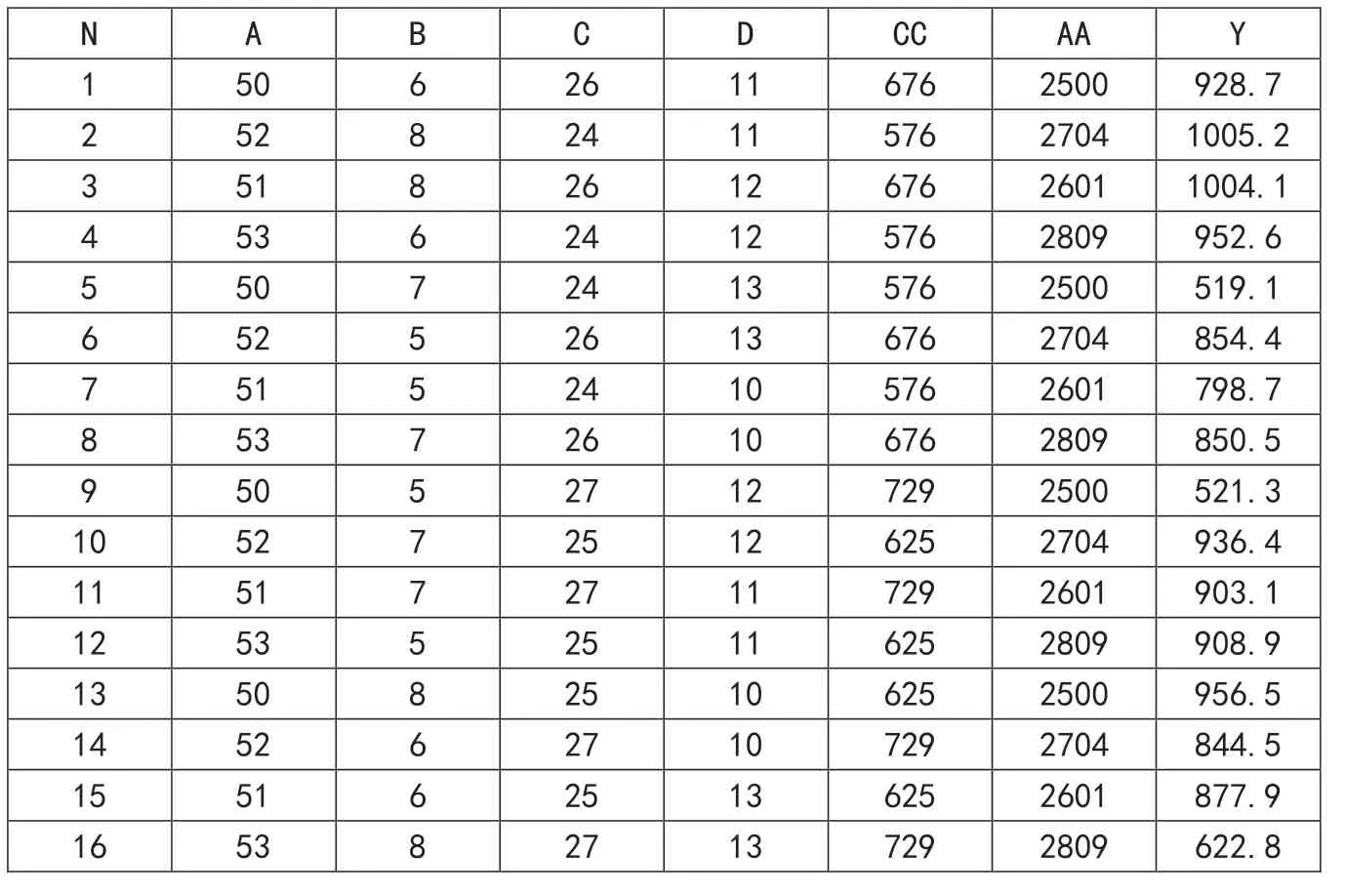
表3 抗拉强度Y“插项”后的excel界面

⑶根据“运筹学”的“多目标决策”的“线性加权和法”，因为本例对两个指标未赋权，直接把两个回归方程相加即可：W=Y+Z，并用excel的“规划求解”选优。由于“规划求解”是局部选优的，分别以初值为0与初值为表2中第3次试验（结果中最好的一次试验）选优，得到的结果都是：当A=51.80951、B=8、C=25.29205、D=10时，有最大值W=1189.739，且抗拉强度Y=1134.494、收缩率Z=55.24561。当然需要验证。

若希望如原文献表明的那样，使收缩率更大些，可以设Z的权重为1.2，这样W=Y+1.2Z，并用excel的“规划求解”选优。分别以初值为0与初值为表2中第3次试验选优，得到的结果都是：当A=51.81814、B=8、C=25.29194、D=10时，有最大值W=1200.793，且抗拉强度Y=1134.445、收缩率Z=66.74819，需要验证。若考虑仍用原来因素水平值，又靠近最优组合的情况，即A=52（A3）、B=8（B4）、C=25（C2）、D=10(D1)，用W=Y+1.2Z拟合的结果是：W=1192.672、Y=1125.174、Z=67.49833，需要验证。如以原文所选最佳组合拟合，得W=1021.461，且抗拉强度Y=960.2488、收缩率Z=61.21187，与实测值颇为接近。

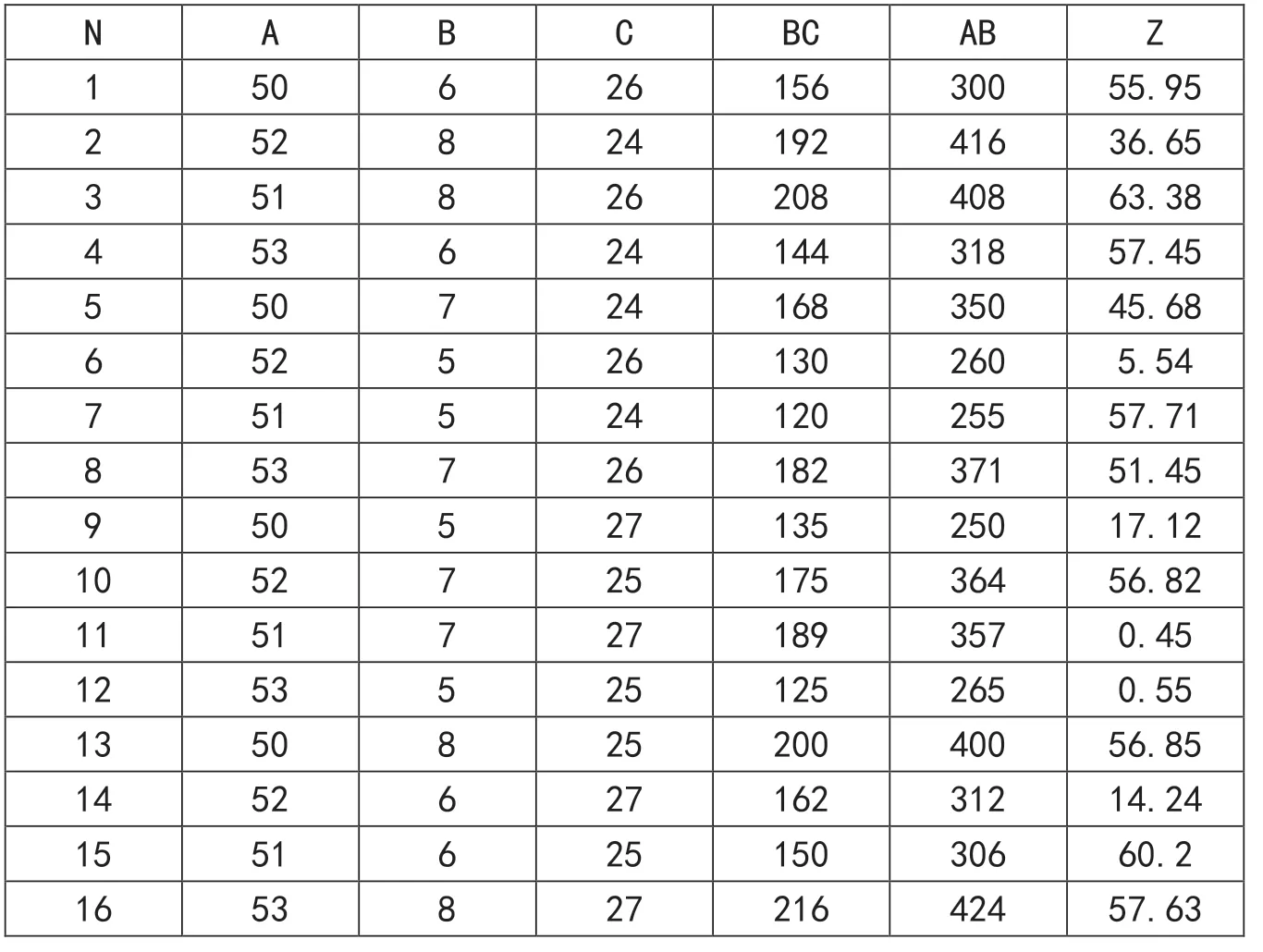
表4 收缩率Z“插项”后的excel界面

3.讨论

客观地讲，回归方程Y和Z里面虽然包含了有意识插入的平方项、交互作用项，比未“插项”前拟合优度改进很多，但严格来说不是拟合得很好的。如Y的图2方差分析表中，残差平方和占总计平方和的比例=31.4%，Z的相应比例=37.0%，这都说明回归方程是“失拟”的（工程上一般要求这个比例在5%～10%之间）。之所以未能拟合得更好，可能跟这个试验性质本身有关，与4个水平的因素趋势图还不善于“插项”有关。本文用“因素趋势法”获得的最佳参数组合，无论是Y和Z等权的，还是Z加权为1.2的，都是L16（45）中原没有的。不但追求的两个指标可能更好，而且还能兼顾能耗、时耗，因此值得关注和验证。