指向数学文化育人的教学实践——以“平方根”的教学为例*

潘金城 (江苏省扬中市新坝中学 212200)

庄志红 (江苏省镇江市教育科学研究中心 212008)

1 引言

数学文化是指数学的思想、精神、语言、方法、观点，以及它们的形成和发展，还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动．丁石孙教授曾说：“我们长期以来，不仅没有认识到数学是一种文化，而且这种状况在相当程度上影响了数学研究和数学教育．”因此，数学文化融入数学课程内容、融入数学教学活动，引导学生感悟数学的自身价值、科学价值、社会价值与精神价值显得尤为必要．本文以“平方根”教学为例，探讨如何基于数学文化设计数学教学活动．

2 教学简析

“平方根”是学生进入初中阶段所学的新概念，是继认识自然数、分数、负数后接触无理数的开始，对后继学习立方根、二次根式、一元二次方程的解法有着重要影响．现行苏科版八年级上册教材将“平方根”的内容安排在继“勾股定理”学习后“实数”单元的第1节(2课时)，其教学起着统领意义．

为此，确定如下教学目标：(1)通过数的发展史感受研究“数的开方”的必要性，了解平方根、算术平方根概念；(2)通过介绍“方根符号历史”认识根号，并会用根号表示平方根和算术平方根；(3)基于数的运算发展史，了解开方与乘方之间的内在关系，会用平方运算求一些非负数的平方根和算术平方根；(4)借助跨学科问题的解决感受平方根应用的广泛性．

3 教学设计与实施

由于“平方根”是“实数”单元的第1节内容，既是“有理数”认识的后续，又对本单元内容的学习起着统领作用．这节课的目标之一就是教师要引导学生从知识的发展性和完备性认识数，让学生知道为什么学、学什么、怎样学，同时从大的知识框架下理解本章学习的重要性和目的性．本节课运用汪晓勤教授所提出的“点缀式、附加式、复制式、顺应式和重构式”融入现行数学课程，发挥各类素材的学科育人功能，改造和运用数学文化素材，从“情境引入、探究释疑、学以致用和总结提升”四个活动设计教学，提升数学育人的实效．

3.1 情境引入

情境1 观察表1，你知道数是怎样发展的吗？

表1 数的起源与发展

设计说明以“点缀式”介绍数的发展，让学生知道认识数的过程漫长，感受到分数的产生源于“分”，引进分数线“—”表示两整数不能整除；负数的产生源于“盈亏”和“解方程”，引进负号“-”表示不够减．以“附加式”的方式介绍公元前5世纪毕达哥拉斯学派的希伯索斯发现并证明了正方形的边长与它的对角线不可公度，从而引发“第一次数学危机”，让学生感受无理数的发现曲折．对数学发展历史以“复制式”将数进行分类，引导学生自主构建实数体系，为系统学习实数启航．

情境2 观察“毕达哥拉斯螺线”(图1)，试填写表2，你是怎样计算的？你发现了什么？能提出什么问题？

表2

图1

设计说明利用“毕达哥拉斯螺线”图，以“复制式”设计情境2，激活学生的元认知，让学生发现x1,x2,x4,x5对应线段与x3对应线段一样客观存在，但长度难以捉摸，由此激发学生产生认知冲突．在此基础上，教师顺势利导提出一般性研究问题：当x2=a时，x是什么数？

3.2 探究释疑

活动1 当a满足什么条件时，存在x使得x2=a．

设计说明数的发展史告诉我们：在中国古代，负数的出现与方程有直接关联．以知识的逻辑顺序和学生的心理发生顺序“重构”历史，提出探究主题：如果从方程视角看“x2=a”，那么我们就得思考x是否一定存在；如果存在，怎样求出未知数x的值？引导学生从x与a的依存关系发现“x的存在性与a的符号之间的关联”，进一步理解平方运算是研究开平方运算的前提．

活动2 填表：请同学们分别列举a的不同的值，尝试求x的值．

a=x2x

设计说明从数学运算发展史可看出：减法的研究基于加法，除法的研究基于乘法．学生可以感受到求未知数x值应该基于平方运算，为此设计了“以开放的形式让学生自主探究a和x的取值”.学生在独自取值填表时会做大量的思考，获取很多有用的信息，如描述平方根的定义，通过举例知道平方根互为相反数的关系，能感受a≥0的必要性．在此基础上获得“平方根的性质”便水到渠成．

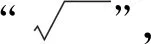
3.3 学以致用

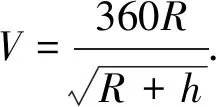
(1)若h=1 700 km，求V的值；

(2)若我国空间站距地面的高度为400 km，估计空间站绕地球一周需要多少分钟？

设计说明数学在人类生活、科学技术、社会发展中的贡献和意义及与数学相关的人文活动都属于数学文化范畴，基于数学文化的知识应用更具有内容的趣味性、素材经典性和思维的挑战性．为此，我们对文[1]素材以“顺应式”的方式改编为问题1，其价值为：一方面设计切合时代背景的空间站问题，激发学生爱国之心与报国之志，充分体现情境育人价值；另一方面将平方根融于科技，加强知识在实际问题中的运用，体现“三会”数学核心素养，发挥学科育人价值．

问题2面积为72.5的正方形边长更接近8还是更接近9？

设计说明以如何判断两个平方根数与某个自然数的大小为问题引发学生的认知冲突，从而抓住机会学习新数．这样的设计不仅是为了唤起学生学习的积极性，更重要的是使得学生对知识的认识能够更加深入．

3.4 总结提升(略)

4 教学思考

“平方根”是概念课教学的典型，它与“有理数”“分式”“根式”“方程”等内容一样在初中“数与代数”中起到举足轻重的作用，是融入数学文化元素、体现数学文化价值的重要载体．因此，教师不仅要理解数学文化的知识成份，更要去挖掘数学文化的观念成份，即从关注数学思想、精神，关心学生的情感、态度和价值观的视角设计和实施数学课堂教学，以达到数学学科育人的目的．下面从三个维度进行分析．

4.1 与原编教材内容的对比看——由“知识”走向“育人”

原编教材中“平方根”的内容是“引入、概念、例题、练习”，素材的选择聚焦知识技能，概念的探索体现“短、平、快”，旨在强调让学生“学会”和“会用”，反映数学“硬”的特质．从历史视角剖析平方根，不难知道平方根的发现是人类对知识无限向往、对真理不懈追求，充满爱恨情仇的发展史，体会到数学“柔”的特质．古代数学家艰辛付出的历史虽然不能重复，但其精神能够激励当下学生学习数学的热情．从生活视角审视平方根，不难感受平方根概念提出后的近代数学研究成果促进和改变人类社会的生活．道路虽然曲折漫长，但给学生播下数学能够创造美好生活的信念．由此可见，数学文化融入课程让学生感悟到知识的发生是自然的，知识的应用是广泛的，知识的力量是无穷的．

4.2 与传统教学设计的比较看——由“实用”趋向“文化”

对于“平方根”的教学设计，大多数教师能“依标扣本”，较好地体现知识与技能目标，凸显“实用”价值趋向．笔者近期听了7节“平方根”教学的起始课，对于“为什么学”，四位教师设计了“算”(已知直角三角形两直角边，求斜边长)，两位教师设计了“拼”(用四个腰长为1的等腰直角三角形拼正方形，求边长)，只有一位教师基于“数学文化”来设计(回顾数的发展史，提出研究新数的必要性)．对于“怎么学”即如何探究平方根的概念，7位教师的设计都没有思考为什么古人把“x2=a”称作“x为a的平方根”，没有从“方程”的视角审视“x2=a”，因而设计碎片化，主线不清晰．解方程(组)是负数产生的根源，平方根概念的研究亦如此．对于“如何用”，教师的选材都基于课本“研究观测者视线达到的最远距离与观测点高度、地球半径之间关系”这个问题，但其缺陷在于数据是“凑”好的，感受不到平方根表示的价值；另外，问题的背景比较俗套，没有融入现代元素，很难激发学生的求知欲．由此可见，一线教师运用数学文化设计教学的意识比较缺乏，因而站位不高，思想封闭．基于数学文化设计教学则能打通学生的认知障碍，丰富学生的思维，增强学生学好数学的信心，充分彰显文化价值．

4.3 从学生课堂反馈的情况看——由“习得”转向“悟得”

在反思提升环节，笔者让学生谈谈学习本节课的收获．

生3：我体会到了平方根在生活中的应用价值和数学中的思维价值．如科学家设计空间站就用到了平方根的知识．我想到了物理电功率公式：P=I2R，若已知电功率和电阻大小，求电流I的值就需要开平方知识．

生4：我想问平方根的概念是怎样产生的？2在实数范围有平方根，但在有理数范围内没有平方根；同样的，-1在实数范围内没有平方根，有没有更大的数的范围，使得-1有平方根？

从这些学生代表的回答看，学生不仅习得了平方根的概念与性质，还悟得基于数学文化的新收获：数学家的追求真理的可贵品质、开更高次方的研究方法、数系还可能进一步扩大,等等．试想，如果没有基于数学文化的教学设计，学生的想象力、思维力和联系沟通能力还能如此丰富吗？

5 结语

基于数学文化的教学活动设计与实施的路径有助于教师在学科核心素养的指向下，挖掘显性与隐性的文化素材，系统地梳理数学文化中所蕴含的知识结构与数学观念，重视数学与文化背景、与现实生活、与其他学科的关联，进一步更新教育观念、优化课程内容、改变学习方式，促进学科育人目标的达成．