一类非线性的带有变时滞的随机微分方程的数值分析
2021-12-17李燕吴浩沙翔高帅斌
李燕,吴浩,沙翔,高帅斌*
(1 华中农业大学 理学院,武汉 430072;2 中南民族大学 数学与统计学学院,武汉 430074)
1 相关知识
随机时滞微分方程在许多领域有着重要的应用,当时滞随着时间变化而变化的时候,对方程的研究更具有现实意义[1]. 方程的解析解在很多情况下是无法计算出来的,此时可以用数值解来逼近解析解[2-4].文献[5]研究了局部Lipschitz条件下数值解的强收敛问题,为随机微机方程数值解的研究开启了新的篇章. 当漂移项系数和扩散项系数均超线性增长时,文献[6]建立了带有常时滞的随机微分方程的截断型θ-EM算法并给出了收敛率. 当θ=0时,截断型θ-EM算法退化成截断型EM算法. 文献[7]和[8]分别给出了截断型EM算法和它的收敛率. 文献[9]得到了带有Poisson跳的混杂随机时滞微分方程的截断型θ-EM算法的收敛率. 文献[10]分析了带有变时滞的随机微分方程的EM数值解的收敛性.
在文献[6]的基础上,本文给出了带有变时滞的随机微分方程的截断型θ-EM算法,并得到了数值解的收敛率. 最后,通过一个简单的例子说明了算法的有效性.
2 主要结论
在本文中,给出相关符号规定.若x∈n,则|x|表示Euclidean范数.若A是矩阵,则|A|表示其迹范数,即若a,b是实数,则a∧b=min{a,b},a∨b=max{a,b},⎣a」表示不超过a的最大整数,令+=[0,+∞),若H是一个集合,则IH表示其示性函数,这意味着,当ω∈H时,IH(ω)=1,否则IH(ω)=0.令C表示一个任意可变的正常实数.
设(Ω,,{t}t≥0,)是一个完备的概率空间,其σ代数流{t}t≥0满足一般条件,是定义在上的期望,设C([-ρ,0];n)是从[-ρ,0)映射到n上的连续函数族,其范数设n)是0可测的C([-ρ,0];n)值的随机变量族,且‖ξ‖p<∞.设B(t)=(B1(t),B2(t),…,Bm(t))T是m维Brownian运动.
考虑带有变时滞的随机微分方程:
dx(t)=f(x(t),x(t-ρ(t)))dt+g(x(t),x(t-ρ(t)))dB(t),t≥0,
(1)

为了得到θ-EM算法的强收敛率,对漂移项系数和扩散项系数施加若干条件.
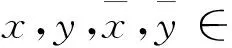

在(A2)之前,引入记号u. 设u是连续函数U∶n×n→+的函数族,其中函数U需满足条件:存在一个常数κb,使得对于任意的x,y∈n且|x|∨|y|≤b,有U(x,y)≤κb|x-y|2.
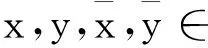
(A3)存在K2>0,p>q>2,使得对于任意的x,y∈n,有:
(A4)时滞函数ρ(·)是正的、有界的且可微的,并且它的导数也是有界的,即:
由(A4)可知,存在一个常数K3>1,使得:
|ρ(t)-ρ(s)|≤K3|t-s|,∀t,s∈[0,T].
(A5)存在常数K4>0和γ∈(0,1],使得当t,s∈[-ρ,0]时,有:
|ξ(t)-ξ(s)|≤K4|t-s|γ.
下面开始定义截断型θ-EM算法.首先,选取一个严格单调递减的函数φ:(0,1]→(0,∞),使得:
(2)
其中,Kφ(Δ)是依赖于φ(Δ)的函数.对于给定的步长Δ∈(0,1),定义截断映射:
(3)
其中,当x=0时,设x/|x|=0.定义截断函数:
fΔ(x,y)=f(πΔ(x),πΔ(y)),
gΔ(x,y)=g(πΔ(x),πΔ(y)).
(4)
假设存在正常数M0和M′使得Δ=T/M′=ρ0/M0.定义tk=kΔ,k=-M0,-M0+1,…,-M′-1.当k=-M0,-M0+1,…,0时,令XΔ(tk)=ξ(tk).
定义:
XΔ(tk+1)=XΔ(tk)+θfΔ(tk+1,tk-⎣ρ(kΔ)/Δ」+1)Δ+(1-θ)fΔ(tk,tk-⎣ρ(kΔ)/Δ」)Δ+gΔ(tk,tk-⎣ρ(kΔ)/Δ」)ΔBk,
(5)
其中,定义:
(6)
则在时间和路径上均连续的数值解定义为:
xΔ(t)=ξ(0)-θfΔ(ξ(0),ξ(-ρ0))Δ+
θfΔ(xΔ(t),xΔ(t-ρ(t)))Δ+


(7)
可以发现xΔ(tk)=XΔ(tk).为了方便,记:
yΔ(t)=xΔ(t)-θfΔ(xΔ(t),xΔ(t-ρ(t)))Δ,
(8)
和
(9)
引理1假设条件(A1)~(A3)成立,则方程(1)在t≥-ρ0上有一个全局唯一解x(t),并且:

(10)
采用与文献[6]的引理2.2与引理2.3相同的方法,可以得到下面引理.
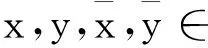
(11)
和
(12)
由引理2可得:
|fΔ(x,y)|∨|gΔ(x,y)|≤
2Kφ(Δ)(|x|+|y|)+(|f(0,0)|+|g(0,0)|).
(13)
引理3假设条件(A3)成立,对于任意的x,y∈n和Δ∈(0,Δ*),有:
(14)

下面引理的证明与文献[9]的引理5相似,此处省略.为了方便,记:
K(t)=⎣t/Δ」Δ,∀-ρ0≤t≤T.
引理4假设条件(A1)成立,对于任意的p≥2,t∈[0,T]和Δ∈(0,Δ*),有:
(15)
引理5假设条件(A1),(A3)与(A4)成立,则有:

(16)
证明由(7)式可得:

(17)
(18)
由引理2、引理3、Young不等式和(2)式可得:

ρ(s)))Δ|p-2·(1+|Z1(s)|2+|Z2(s)|2|)ds≤
C·
(|xΔ(s)|p+|xΔ(s-ρ(s))|p)+|Z1(s)|p+
|Z2(s)|p|)ds≤
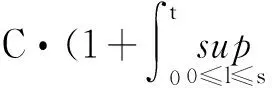
(19)
另外,
H2≤C
Z1(s)|·|fΔ(Z1(s),Z2(s))|ds+C
|fΔ(Z1(s),Z2(s))|ds=:H21+H22.
(20)
由引理2、引理4、Young不等式和(2)式可得:

Z2(s))Δ‖κ(s))]ds≤



|Z1(s)-θfΔ(Z1(s),Z2(s))·Δ|p-2)ds+

(21)
同(21)式的过程相似,由引理2、引理4和(2)式可得:
(22)
把(19)~(22)式代入(18)式可得:
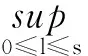
由基本不等式|a-b|≥21-p|a|p-|b|p和(13)式可得:
|yΔ(t)|p≥21-p|xΔ(t)|p-θpΔp|fΔ(xΔ(t),xΔ(t-
2p-1θpΔp(|f(0,0)|+|y(0,0)|).
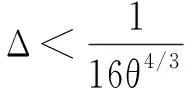

运用Gronwall不等式可得(17)式.
引理6假设条件(A1)~(A4)成立.对于任意的p≥2,t∈[0,T]和Δ∈(0,Δ*),有:
(23)
和
(24)
证明由引理4和引理5,通过条件期望的性质可得(23)式,再用引理5中的证明技巧可知:
引理7假设条件(A1)~(A4)成立.对于任意的p≥2,t∈[0,T],和Δ∈(0,Δ*),有:
(25)
证明由文献[9]的引理5可得,对于任意固定的t∈[kΔ,(k+1)Δ)有:
C|yΔ(t-ρ(t))-yΔ(kΔ-⎣ρ(kΔ)/Δ」Δ|p≤

由(A4)和不等式ρ(kΔ)-Δ≤⎣ρ(kΔ)/Δ」Δ≤ρ(kΔ)可得:
|ρ(t)-⎣ρ(kΔ)/Δ」·Δ| ≤
所以可得|ρ(t)-⎣ρ(kΔ)/Δ」·Δ|≤(K3+1)Δ,
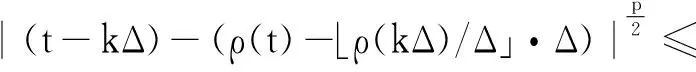
因此,由引理5可得:

采用引理1和引理5中的证明技巧可以得到下面的引理.
引理8假设条件(A1)~(A4)成立.对于任意的L≥‖ξ‖,定义τL=inf{t≥0:|xΔ(t)|≥L}和τΔ,L=inf{t≥0:|xΔ(t)|≥L},然后可得:
引理9假设条件(A1)~(A5)成立.令Δ∈(0,Δ*)充分小使得φ(Δ)≥L∨‖ξ‖,则有:
(26)
其中τ:=τL∧τΔ,L.
证明记eΔ(t)=x(t)-yΔ(t),t∈[0,T].由fΔ(·,·)与gΔ(·,·)的定义可知,对于任意的0≤s≤t∧τ,有:
fΔ(Z1(s),Z2(s))=f(Z1(s),Z2(s)),
gΔ(Z1(s),Z2(s))=g(Z1(s),Z2(s)).
|g(x(s),x(s-ρ(s)))-gΔ(Z1(s),Z2(s))|2]ds+
|g(x(s),x(s-ρ(s)))-g(Z1(s),Z2(s))|2]ds+
(27)
由(A2)和引理6、引理7可得:
J1≤2K1(|x(s)-Z1(s)|2+|x(s-ρ(s))-
Z2(s)|2)ds+2(-U(x(s),Z1(s))+
U(x(s-ρ(s)),Z2(s)))ds≤
4K1(|x(s)-xΔ(s)|2+|xΔ(s)-
Z1(s)|2+|x(s-ρ(s))-xΔ(s-ρ(s))|2+
|xΔ(s-ρ(s))-Z2(s)|2)ds+
C(|x(s)-xΔ(s)|2ds+C·Δ·

(28)
相似地,由引理2、引理6和引理7得到:
J2≤CKφ(Δ)|xΔ(s)-Z1(s)|·(|x(s-ρ(s))-Z2(s)|+|x(s)-Z1(s)|)ds≤
C
|x(s-ρ(s))-Z2(s)|2)ds≤

(29)
同理,由引理2、引理6、引理7和(8)式可得:
J3≤C
C(|x(s)-Z1(s)|2+|x(s-ρ(s))-

(30)
把(28)~(30)式代入(27)式可得:

因此,可得:

应用Gronwall不等式可知,对于任意的t∈[0,T],有:
即是所需结论.
下面的定理1给出了L2空间上的收敛率.
定理1假设条件(A1)~(A5)成立.对于充分小的Δ∈(0,Δ*),假设存在一个常数c0>0,使得:
(31)
则对任意的T>0,有:
(32)
证明设δ是任意正常数,由Young不等式可得:
因此,可得:
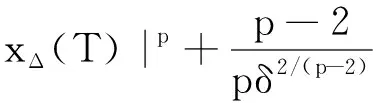
由引理1和引理5可得:
|x(T)-xΔ(T)|p≤C.
由引理8可得:
{τ≤T}≤{τL≤T}+
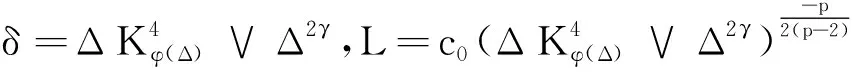
(33)
由(31)式可知:
由引理9和(33)式得到:
证毕.
3 实例
考虑非线性的带有变时滞的标量随机微分方程:

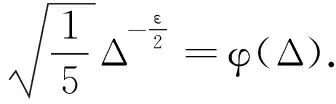
|x(T)-xΔ(T)|2≤CΔ(1-4ε)∧2γ.
