混合效应模型的双MCP惩罚分位回归研究
2021-12-17罗幼喜
周 霖,罗幼喜
(湖北工业大学理学院,武汉 430068)
随着数据收集和存储能力的不断进步,数据获取的方式和途径越来越多,数据之间的关系也越来越复杂.如何针对高维复杂数据进行统计建模分析是一个亟待解决的问题.原始的变量选择方法由于其方法本身的局限性,在面对高维复杂数据时显得力不从心.近些年,随着对变量施加正则化惩罚理论的提出,不同的惩罚方法被运用到变量选择的领域内.Ridge回归采用L2正则化惩罚,通过岭迹的图像来判断冗余变量,从而降低变量之间共线性的影响.Tibshurani[1]提出了LASSO (least absolute shrinkage and selection operation)回归,采用L1正则化惩罚,在估计回归系数时自动对变量进行选择,将冗余变量的系数压缩为0.LASSO惩罚函数为凸函数,且是有偏估计,通过减小预测模型的方差达到降低预测总误差的目的,但容易存在过度压缩系数的缺点.为了进一步降低预测总误差,Fan和Li[2]提出了SCAD惩罚,它不仅对于很小的回归系数压缩到0,而且是一种近似无偏估计.Zhang[3]提出的MCP惩罚(minimax concave penalty),采用对回归系数有差别的惩罚,在保留SCAD惩罚优点的同时得到更加精确的估计.基于此,越来越多的学者将MCP惩罚运用在各个领域研究中,在此基础上进行优化,并在图像去噪[4]和图像重建[5]中有了较大的进展.
在混合效应模型中,考虑到样本的数据有一定的关联性,在模型中添加了随机效应项.如果仅考虑固定效应而忽视随机效应的影响,则会给最后的估计带来偏差,但是无关的随机效应太多则会导致求解过程中随机效应的协方差阵不可逆,不利于估计,因此如何解决个体的随机效应所带来的误差是高维混合效应模型进行变量选择的关键.
将混合效应模型和分位回归联合起来,在不同的分位点进行变量选择是一个新兴的研究领域.现有的文献中,多数学者都是对随机效应进行L1正则化[6-8],该方法只能剔除冗余的随机效应,减少随机效应的数量,但是无法选择出固定效应中的重要预测变量.罗幼喜[9]针对此问题提出来一种双Lasso正则化分位回归法(DLQR),对模型中的固定效应和随机效应同时施加L1惩罚,使得模型的冗余度大大降低.但是L1正则化得到的结果为有偏估计,本文以MCP正则化替代L1正则化,提出双MCP正则化分位回归法(DMQR).
1 模型与方法
传统的线性混合效应模型为:


在实际生活中,数据往往存在异方差或者尖峰、后尾等情况,使得传统的均值回归效果不好,且一条回归线所反映的信息也是有限的,分位回归相对于均值回归,其应用条件更加宽松,依据不同的分位数,对自变量进行回归,能更好的描述自变量对因变量的变化范围以及条件分布形状的影响.Koenker和Bassett[10]提出线性分位回归:
Q(τ)=inf(y:F(y)≥τ),
其中,inf表示最大下界,Koenker[6]考虑了含随机截距的条件分位回归模型:
i=1,2,…,n,
(1)
并提出对个体波动施加L1正则化压缩的分位回归方法,数学表达式如下:
(2)
在实际问题中,有时个体效应不仅对模型截距有影响,也可能对模型的斜率有影响,将上述回归模型推广到既包含随机截距又包含随机斜率的条件分位回归模型,即在给定个体随机效应αi条件下,响应变量的τ分位回归函数为:
j=1,2,…,ni;i=1,2,…,n,
(3)
罗幼喜[9]提出了DLQR方法,对个体效应施加L1惩罚以防止模型的过拟合,同时对固定效应施加L1惩罚来剔除冗余变量,选出重要的自变量,减少模型的冗余度,即极小化下式:

(4)
其中,λα为对个体效应施加的惩罚参数,λβ为对固定效应施加的惩罚参数.ρτ(·)为分位回归函数,其表达式如下:
Lasso惩罚函数为凸函数,且是有偏估计,通过减小预测模型的方差达到降低预测总误差的目的,但容易存在过度压缩系数的缺点.为了进一步降低预测总误差所提出的SCAD惩罚,它不仅对于很小的回归系数压缩到0,而且是一种近似无偏估计.之后提出的MCP惩罚,采用对回归系数有差别的惩罚,在保留SCAD惩罚优点的同时得到更加精确的估计.MCP惩罚函数的数学表达式如下:
(5)
上式中,λ为正则参数,用来调整惩罚力度;a为调整参数,用来控制惩罚范围.其惩罚力度为:
(6)
当|β|≤aλ时,MCP的惩罚力度会随着参数绝对值的增大而减小,当|β|=0时其惩罚力度最大为λ,当|βi|=aλ时,其惩罚力度变为0,当回归系数继续增大时其惩罚力度保持为0不变.将Lasso与MCP惩罚的惩罚力度可视化如下图1所示.

图1 Lasso与MCP惩罚力度图Fig.1 Lasso and MCP penalty intensity diagram
从上图可以看出,Lasso对回归系数采用恒定的惩罚力度,而MCP对回归系数采取有差别的惩罚,当|βi|≥aλ,其惩罚力度为0,其参数的估计类似于最小二乘估计,其拟合的系数结果更精确.基于此,本文将DLQR法中L1惩罚替换为MCP惩罚,提出了双MCP正则化的分位回归方法(DMQR),即极小化下式:

(7)
其中,Pλβ(|βl|)表示对固定效应施加MCP惩罚,Pλα(|αit|)表示对个体效应施加MCP惩罚.
2 回归系数估计方法与正则化参数的选取准则
2.1 回归系数估计方法
针对高维非凸惩罚的分位回归问题,Wang和Peng[11]提出了迭代坐标下降(QICD).QICD算法将MM算法与坐标下降算法相结合.具体地说,首先用一个优化函数来替代非凸惩罚函数,并得到新的目标函数.然后,将关于目标参数的每次和每次循环替代所有参数,直到收敛为止.对于每个坐标下降步骤,只需要计算单变量加权中位数,可确保快速计算.具体计算流程图见表1.双MCP正则化分位回归估计可以采用交替迭代算法求解,即每次只求解单个MCP正则化分位回归,具体迭代算法求解见表2.

表1 QICD 算法伪码表Tab.1 QICD algorithm pseudo code table

表2 双MCP惩罚分位回归迭代算法Tab.2 Double MCP penalty quantile regression iterative algorithm
2.2 正则化参数选取准则
选择合适的正则化参数对于MCP惩罚的效果很关键.在DMQR法中一共有4个正则化参数,即Pλβ(|βl|)中的aβ和λβ,Pλα(|αit|)中的aα和λα,为简化计算量和降低模型的复杂度,一般建议aα=aβ=3.0[12].此时需要选择的正则化参数只有两个,即调整固定效应的惩罚力度的λβ和调整个体效应惩罚力度的λα.运用上述迭代算法,每次迭代过程中,只用考虑单个正则化参数,使得参数选取的复杂度大大降低.
Wang[13]在Fan和Li[14]的基础上提出了具有一致性的BIC法用于正则化参数选取.其数学表达式为:
(8)

(9)
其中,
(10)

3 计算机模拟比较研究
3.1 稀疏模型下两种惩罚方法的比较
数据生成的公式如下:
(11)
表3给出了τ=0.25,0.5,0.75三个不同分位点下的模拟结果,重复模拟次数为100次,衡量模型精度的均方误差(MSE)定义如下:
(12)

C1=重要预测变量被正确选择个数/真实重要预测变量总个数,
C2=冗余预测变量被正确排除个数/真实冗余预测变量总个数.
C1和C2取值介于0和1之间,C1越接近1 表示其挑选重要预测变量的能力越强,反之越差;C2越接近1表示其排除冗余预测变量的能力越强,反之越差.表3 还给出了100次重复模拟中3 个重要预测变量X1、X2、X5被正确选择和5 个冗余预测变量X3、X4、X6、X7、X8被正确排除的总次数.其中,判断是否选择了某变量是根据对该变量系数估计是否为0 得到的(本次模拟基于R 3.6.2,platform为x86_64-w64-mingw32条件下实验运行).

表3 不同条件下两种惩罚分位回归结果Tab.3 Regression results of two penalty quantiles under different conditions
从变量选择的角度分析,在不同的σ取值下,DLQR和DMQR都能准确的选择出模型中的重要预测变量,但是在排除冗余变量方面,DLQR最多只能准确排除75%左右的冗余变量,而DMQR则能正确排除90%以上的冗余变量,使模型中的干扰变量更少,具体效果见图2.

图2 变量选择效果Fig.2 Variable selection effect
从估计的精度来看,在τ=0.5;σ=1时,DMQR的估计精度最优.且在不同分位点,不同的σ取值时均比同等情况下的DLQR估计精度要高,且方差更小,具体效果见图3.

图3 两种惩罚精度对比图Fig.3 Comparison of two types of penalty accuracy
保存每次DMQR法模拟产生的30个6维行向量αi(i=0,1,2,3,4,5),得到一个30×6的α矩阵,即为随机效应α的估计值,计算每一列的均值和方差作为随机效应参数的一个估计.在不同分位点和不同信噪比下取100次模拟的平均值作为最后随机效应α均值和方差的估计值,具体数据如下表4(上方数据为均值,括号内的数字为方差).

表4 随机效应估计表Tab.4 Random effect estimate table
从均值的角度分析,在不同的分位点和不同的信噪比下,随机效应系数α的均值都接近于0,拟合效果较好;从方差的角度分析,在不同分位点和不同信噪比下,α4,α5方差的拟合效果都很好,方差也接近于0,其他随机效应系数的方差,随着信噪比σ的增大,模拟效果逐渐降低,在不同分位点,当σ=1时其模拟效果最好,最接近于1,且在τ=0.5;σ=1,模拟效果最佳.
τ=0.5时,在不同信噪比下,保存每次模拟最后一步惩罚参数λα,λβ的值,100次模拟下,惩罚参数的箱线图如图4所示.

图4 惩罚参数选取箱线图Fig.4 Penalty parameter selection box plot
从上图可以看出,随机效应的惩罚参数λα其分布较为密集,其上四分位点与下四分位点包含的区间更小,且惩罚参数基本集中在0.09左右,固定效应的惩罚参数λβ其上四分位点和下四分位点所包含的区间更大,且其最大值与最小值之间的差距相较于λα更大.
3.2 不同误差分布时估计的比较
下文在不同误差分布情形下比较DMQR同其他几种分位回归方法在变量选择和估计精度上的表现,数据生成的模型为式(11),自变量系数设置为稠密、稀疏、高度稀疏三种不同情况:
1)稠密模型:β=(0.85,0.85,0.85,0.85,0.85,0.85,0.85,0.85);
2)稀疏模型:β=(3,1.5,0,0,2,0,0,0);
3)高度稀疏模型:β=(5,0,0,0,0,0,0,0).
取σ=1,τ=0.5,D=diag(2,2,2,2,0,0),取误差εij分别来自N(0,1),t(3)及Cauchy(0,1)分布.比较的方法有:①普通分位回归(QR);②双Lasso惩罚分位回归(DLQR);③双MCP惩罚分位回归(DMQR).表4、表5、表6给出了各种情况下重复100次的模拟结果.

表5 稠密模型下模拟结果Tab.5 Simulation results under dense model

表6 稀疏模型下模拟结果Tab.6 Simulation results under sparse model
在稠密模型下,所有的变量均为重要预测变量,所以不存在正确排除冗余变量,故C2不存在.从MSE角度来看,不论误差服从何种分布对系数进行惩罚后的模型在精度上面不如直接进行分位回归的模型,DMQR模型和DLQR模型的拟合精度相差不大,主要原因是在稠密模型下,所有变量都不需要进行惩罚,故直接分位回归(QR)得到的结果是最好的.
从误差服从的不同分布来看,当误差服从正态分布时,三种估计方法的精度最高,当误差服从柯西分布时,估计的误差最大,且对系数进行惩罚后,C1的值不能完全达到1.
在稀疏模型下,普通的分位回归(QR)在排除模型中冗余变量的能力为0,因为普通分位回归不能对变量进行选择,只能将所有的变量均视为重要变量保留在模型中.而对系数施加惩罚后的方法则能排除模型中的冗余变量,但是不同惩罚所得到的结果也不同.
从排除模型中冗余变量的能力来看,DMQR剔除冗余变量的效果最好,能剔除90%以上的冗余变量,且在误差服从标准正态分布时的效果最好,达到了94%.而DLQR只能剔除约70%以上冗余变量,从估计的精度来看,DMQR在3种方法中的估计精度最高,且在误差为正态分布时的精度最高,当误差为柯西分布时的精度最低,具体效果如图5.

图5 稀疏模型下拟合估计效果图Fig.5 Fitting estimation effect diagram under sparse model
在高度稀疏模型下,无论误差服从什么分布,DLQR法能剔除约80%以上的冗余变量,DMQR法能剔除约90%的冗余变量,虽然DMQR法的效果仍比DLQR法的结果好,但两者在剔除冗余变量上的差距相较于稠密模型和稀疏模型缩小了许多.在模型的精度上面,DMQR法要优于DLQR法,DMQR法在正态分布时精度最高,误差为0.188,说明DLQR法虽然在高度稀疏模型下能够很好的排除冗余变量,但是对重要变量的拟合精度不高,拟合出来的结果与真实结果差距较大,拟合效果如图6.

图6 高度稀疏模型下拟合效果图Fig.6 Fitting effect diagram under highly sparse model
3.3 高维情况比较
本节在高维情形下考察双正则化分位回归DLQR和DMQR的表现.数据的生成模型仍为式(7),但减少样本量至n=10,m=10,即总样本量为100.在模拟(2)的稀疏模型中额外添加102个独立噪声变量X9,X10,…,X110,所有变量均独立同分布于N(0,0.52),在添加噪声变量后,总的变量个数为110个,大于总样本量.其中重要的预测变量为3个,冗余变量为107个.另外设σ=0.5 ,D=diag(1,1,1,1,0,0).表7给出了两种方法在τ=0.5 、0.9 两个分位点下进行100次模拟估计的结果.
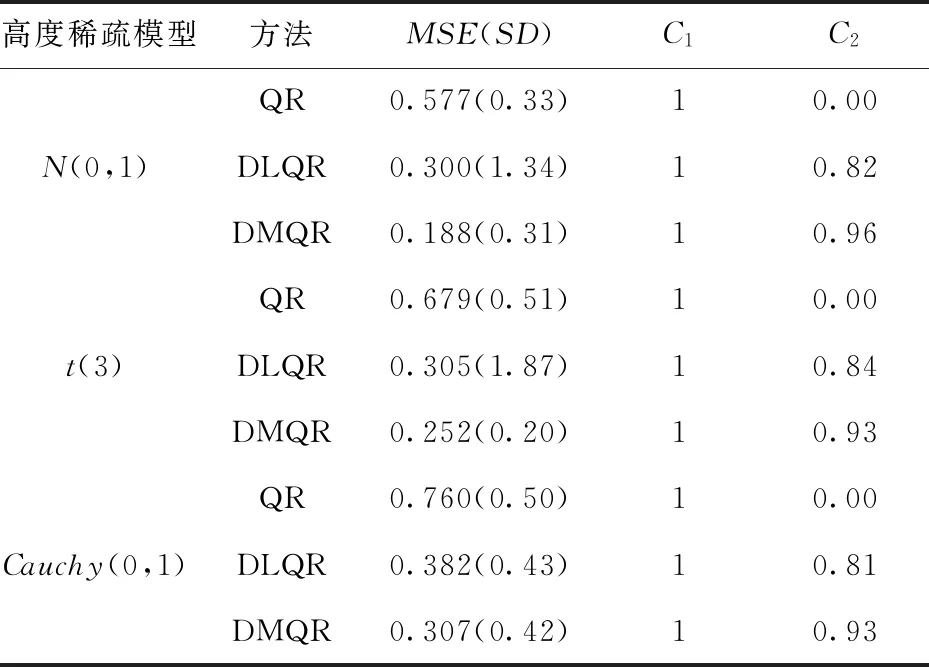
表7 高度稀疏模型下模拟结果Tab.7 Simulation results under highly sparse model
在高维情况下,DLQR法与DMQR法两者的模拟差距非常明显.从变量选择的角度看,DLQR法只能正确剔除约81%的冗余变量,而DMQR法几乎能剔除冗余变量的能力约为90%,且在τ=0.5 时能达到93%.在估计的精度上面,DMQR则要远远好于DLQR,DLQR法在不同分位点的平均误差为5.94,而DMQR法的平均误差仅为2.82.两种方法在τ=0.5 时估计的精度均优于τ=0.9时的精度.

表8 高维情形不同分位点下估计结果Tab.8 Estimation results under different quantiles in the high-dimensional case
4 结论
本文在罗幼喜[9]提出的双Lasso的基础上改进了惩罚方法,提出了双MCP正则化分位回归(DMQR).通过模拟结果可以发现,不论模型是稠密模型、稀疏模型还是高度稀疏模型,改进后的方法不论是在正确选择模型中重要变量方面还是剔除冗余变量方面均比原来的方法要好,且模型的精度更高.DMQR法对误差有很好的稳健性,在正态分布下拟合的效果最好.在高维情况下,DMQR相对于DLQR法的优势更大,基本上能完全选中模型中的重要预测变量,且排除冗余变量的能力也能达到90%左右,模型估计的精度更是远远大于DLQR法.
