基于ASME-Ⅷ-2的弹塑性棘轮分析实例
2021-12-17魏晓张岚尤琳
魏晓,张岚,尤琳
(山东豪迈机械制造有限公司,山东 青岛 266061)
关键字:弹塑性分析;棘轮分析;有限元
对于压力容器受压元件,通常会受到内压和沿壁厚叠加的循环热应力综合作用。热应力通常会在瞬态工况时产生,例如容器的开车和停工。加热温度或冷却温度的瞬态改变会形成沿壁厚方向的温度梯度。对于设有保温的容器,热量的损耗非常小,在经历温度瞬变后,温度沿壁厚会再次变为均布。因此,对容器或管道进行弹性分析时,由开车的瞬态温度变化产生的应力会在后续的操作中及停车后的一段时间后消失。
当温度载荷为循环工况时,结构可能会发生棘轮失效。棘轮现象是元件受交变机械应力、温度应力或两者同时作用时出现的渐增的塑性变形或应变,而热应力棘轮是由部分或整体的温差应力引起的。棘轮现象的变形特点是每次加载循环的前半周和后半周在结构的不同部位轮流产生塑性变形,最终导致压力容器因渐增性变形而垮塌[1]。
ASME 规范给出了两种分析棘轮现象方法,即弹性分析法和弹塑性分析法,弹性分析是一种近似方法,在大部分情况下偏于安全和保守,对棘轮进行严密的评定应采用弹-塑性分析方法[2]。
在分析设计中,往往通过有限元程序对结构进行热-结构耦合分析对棘轮失效模型进行校核。如果满足以下任何一个条件,则棘轮准则满足。如果不满足下述的棘轮准则,则应修正元件的结构或降低作用的载荷并重新进行分析。①塑性应变为零,即表现为完全弹性行为或弹性安定,该准则最为保守;②弹性核准则,即出现塑性安定;③总体尺寸无永久性改变,即结构无明显渐增性塑性垮塌[3]。
本文对一典型压力容器结构,由所作用载荷的施加、移去和再次施加,采用弹塑性分析以防止棘轮失效。分析结果表明弹性核是存在的,这意味着该结构处于安定状态,不会发生塑性棘轮失效。
除此之外,为了进一步展示弹性核消失和塑性变形递增的现象,将25 mm 的球形封头替换为50 mm 厚的平盖结构。同时为了与弹性棘轮分析方法对比,本文依据规范对模型的关键部位进行线性化路径选取,用弹性分析方法对防止棘轮失效进行评定。结果表明用弹性分析方法与弹塑性分析方法所得结论一致。
该结构包括一圆柱壳和球形封头,三维模型如图1 所示。建模厚度采用去除腐蚀余量并考虑成型减薄量的有效厚度,圆柱壳外径为φ700 mm,壁厚为50 mm,球形封头的厚度为25 mm。

图1 三维模型Fig.1 3D model
设计压力:25 MPa
温度循环范围:22 ~ 300 ℃
1 有限元分析
1.1 模型建立
为了加快求解速度和提高求解精度,根据结构与载荷的对称性,取1/4 模型来进行有限元分析(该模型为轴对称模型,亦可用2D 模型分析,为了更加直观,这里笔者采用了3D 模型)。
1.2 材料定义
采用弹性-理想塑性材料模型,假定材料为某碳钢,屈服强度设置为235 MPa,选择VON-MISES 屈服函数和与之相关的流动准则,应力应变曲线如图2所示,未考虑循环载荷作用下材料的强化行为。另外,还需定义材料的弹性模量、泊松比、线膨胀系数等参 数。
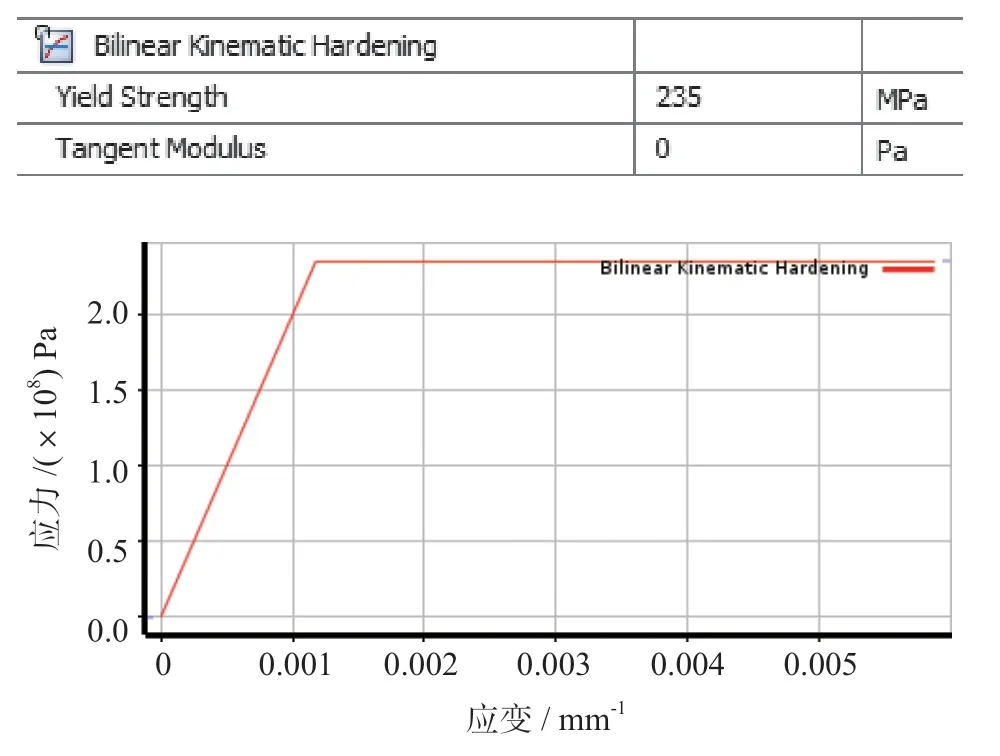
图2 材料定义Fig.2 Material definition
1.3 划分网格
本模型主要采用扫掠网格划分的方法,单元类型为默认的SOLID186 单元。网格划分完成后节点数990 036,单元数为362 538,图3 为有限元网格模型。

图3 划分网格后的模型Fig.3 Model after meshing
1.4 耦合分析
图4 为耦合分析的示意图,先对结构进行多载荷步瞬态温度分析,得到各时刻的温度分布,再将温度分布结果作为载荷条件用于静态结构分析,需要注意的是二者的载荷步和时间需要一一对应,且导入温度载荷时要选择所有时刻的温度计算结果。同时在求解设置中打开大变形开关,考虑几何非线性的影响。
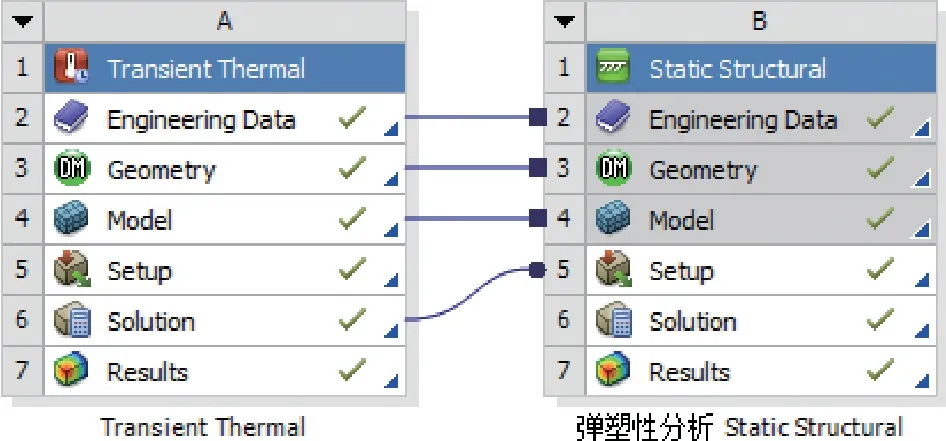
图4 耦合分析Fig.4 Coupled analysis
对于瞬态热分析,内表面温度循环历史如图5所示,考虑前3.5 个循环,分14 个载荷步进行定义。首先因为热介质的加入使设备内壁面升温,升温到300 ℃以后保载一段时间,此时温度沿壁厚的分布逐渐趋于均匀,然后开始卸载所加温度载荷,在卸载的初始时刻,外表面温度仍保持不变,内表面温度瞬间降低到环境温度22 ℃,使得内外壁面产生较大的温度梯度。
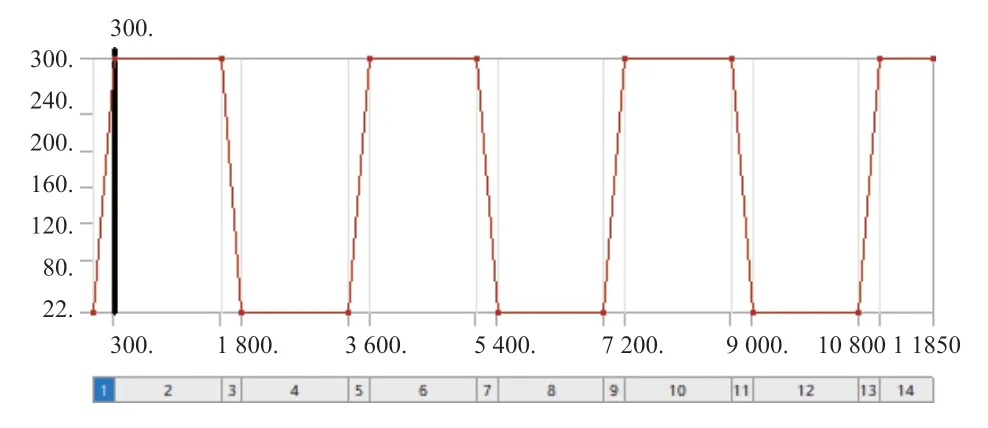
图5 温度载荷Fig.5 Temperature loads
位移边界条件如图6 所示,在两个对称面上施加对称约束,并限制底部端面的轴向位移。在垂直容器内壁面上施加均匀的内压25 MPa,该内压会在壳体中产生平均环向应力,如图7 所示。

图6 约束Fig.6 Constraints
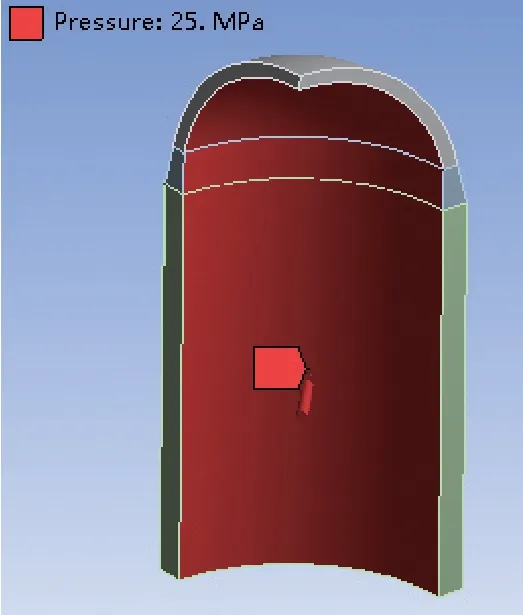
图7 机械载荷(内压)Fig.7 Mechanical load (internal pressure)
3 结果分析
内外壁温度随时间沿壁厚的分布曲线如图8 所示,图9 为温度梯度示意图,可见沿壁厚方向形成了明显的温度梯度。

图8 温度分布曲线(内壁与外壁)Fig.8 Curve of the temperature distribution (inner wall and outer wall )

图9 温度梯度Fig.9 The temperature gradient
图10 所示为最大塑性应变随时间变化曲线,可见在第一循环发生初始的塑性应变后,后续循环没有产生新的塑性应变,三个循环中未出现塑性变形的累积。图11 为弹性核示意图,通过在后处理结果中查看等效塑性应变,并通过Capped Iso-surface 命令仅显示塑性应变为零的区域,便可获得弹性核的云图。可见弹性核在圆柱壳壁厚和球封头处都是连续的,塑性应变仅出现在圆柱壳的内壁以及圆柱壳与球封头连接处的局部区域。故所分析的结构处于安定状态,也就是说在壳体的沿厚度方向的任一截面上都没有发生棘轮现象[4]。

图10 最大塑性应变随时间变化曲线图Fig.10 Curve of the maximum plastic strain along with time

图11 弹性核示意图Fig.11 The elastic core
图12 显示了球形封头顶点处的最大位移在三个循环中随时间变化的曲线,可看出位移增量在第二个循环后变得稳定,没有发生明显渐增性塑性变形。

图12 三个循环中最大位移随时间变化曲线Fig.12 Curve of the maximum deformation of the three cycles along with time
4 与平盖结构的结果对比
为了直观地感受棘轮失效现象,笔者将25mm厚的球形封头更改为50mm 厚的平盖结构,保持圆柱壳尺寸不变,结构如图13 所示。施加相同的温度和压力载荷进行棘轮分析,所得塑性应变随时间的变化曲线和弹性核示意图分别如图14 和图15 所示,平盖中心处最大位移随时间变化曲线如图16 所示。可见在平盖与筒体的连接处及平盖厚度方向上弹性核消失,同时最大塑性应变随时间产生累积,且平盖中心处的最大位移也随着每个循环递增,发生渐增性塑性垮塌,故可知该结构是不安定的,会发生棘轮失效。

图13 平盖结构Fig.13 Flat cover structure

图14 最大塑性应变随时间变化曲线Fig.14 Curve of the maximum plastic strain along with time

图15 弹性核示意图Fig.15 Diagram of the elastic core

图16 三个循环中最大位移随时间变化曲线图Fig.16 Curve of the maximum deformation of the three cycles along with time
5 与弹性棘轮分析方法的对比
为将上述弹塑性棘轮分析的结果与弹性棘轮分析进行对比,根据ASME 的规定,对两种结构用弹性分析的方法进行防止棘轮现象的评定,则应满足ΔSn,k≤SPS,其中一次加二次当量应力范围ΔSn,k是由越过截面厚度最高值导得的一次薄膜应力加一次弯曲应力加二次应力(PL+Pb+Q)组合得到的当量应力范围。SPS为一次加二次当量应力范围的极限,取max[3S, 2Sy];但当屈服强度与最大拉伸强度之比超过0.7 或S为与时间相关的性能决定时,SPS取3S[2]。
同样先进行瞬态温度分析,再进行静态结构分析,时间和载荷步设置依然对应,但弹性棘轮分析方法不再考虑材料的非线性,仅定义材料的弹性模量、泊松比、线膨胀系数等参数。
两种结构的线性化路径如图17 所示。提取各条路径的一次应力加上二次应力ΔSn,k,并比较ΔSn,k和SPS的大小。计算结果和评定结果见表1,评定结果显示球封头结构不会发生棘轮,而平盖结构会发生棘轮失效,这与弹塑性棘轮分析的结果是一致的。

表1 应力评定(棘轮评定)Tab.1 Stress evaluation (ratcheting assessment)

图17 路径定义Fig.17 Definition of paths
6 结论
本文从材料定义、求解设置和结果分析几个方面,对弹塑性棘轮分析进行了详细的描述。除了本文述及的圆筒、球形封头、平盖等结构外,压力容器还会涉及更多复杂的结构和载荷工况,结构通常是超静定的。对于类似相关结构,可以参照该方法进行有限元分析,并结合规范中的弹性核准则,完成棘轮评定。规范规定,在作用最少为三个完整的循环以后,按棘轮准则进行评定。为证实其收敛性,可能需要增加附加的循环次数。但在大多数情况下,通过三个循环就能够确定弹性核是否存在及其分布区域[5]。
通过本例还可以看出,棘轮评定的三个准则间是既有区别又有联系的[6]。零塑性应变准则实际上是弹性核准则的一个特例,即没有发生任何塑性应变,整个结构就是一个大的弹性核,该方法对有些材料来说过于保守。在进行棘轮评定时,总体变形准则与弹性核准则是一致的,当基于弹性核准则结果评定为棘轮时,总体变形就会持续地增大;而当基于弹性核准则结果评定为安定时,总体变形也会很快趋于稳定。
本文只针对棘轮失效模式进行评定,分析过程未考虑计算的完整性,工程中应根据实际情况并考虑多种失效模式进行全面的校核。
