基于ARIMA-BIGRU的船舶航迹预测

于琛，付玉慧，张逸飞，王超

(大连海事大学 航海学院，辽宁大连116026)

船舶航迹预测方法主要分为基于物理运动模型的方法和基于学习模型的方法。总结国内外学者的研究现状[1-5]，大部分学者选用了单一预测模型，但每种类型的模型并不是在所有情况下都表现良好。为了克服单个模型的局限性，有学者提出组合预测的方法，如以LSTM为主、ARIMA(autoregressive integrated moving average model，ARIMA)为辅的组合短期飞行轨迹预测模型[6]。与单模型对比提升了预测的精确度。有学者提出利用LSTM挖掘飞行轨迹中的非线性关系并结合ARIMA挖掘飞行轨迹中的线性关系的组合预测模型，将时间序列分成线性序列与非线性序列，进一步提高了飞行轨迹预测的精度[7]。ARIMA在处理线性时间序列中取得了优良的效果，但对于非线性序列部分的信息无法进行捕捉。BIGRU神经网络是LSTM循环神经网络的变体，能够很好地学习到非线性序列信息，引入注意力机制对GRU神经网络进行权重训练，可以进一步提高预测精度。有学者提出基于BIGRU和自注意力机制的情感分析模型，将注意力机制与BIGRU结合相较于单BIGRU模型预测精度取得了较大的提升[8]。综合以上分析，提出一种基于ARIMA和注意力机制的神经网络组合模型。考虑AIS数据中线性因素及非线性因素对船舶轨迹预测的影响。利用ARIMA良好的线性因素学习能力，初步预测出下一时刻船舶轨迹坐标，进而提取出预测残差，将残差特征输入BIGRU神经网络，结合注意力机制挖掘AIS数据中非线性因素对船舶轨迹的影响。

1 理论模型

1.1 ARIMA模型

时间序列模型ARIMA为差分自回归移动平均模型。分为自回归模型AR、移动平均模型MA、差分I。

AR(p)描述当前平稳序列的值与历史值之间的关系，用变量自身的历史数据对自身进行预测。p为阶数，表示采用p个时间点的历史值来预测当前值。

MA(q)为自回归模型中误差项的累加，q为移动平均项数。I(d)为变量的差分，d为差分的阶数。通常采用自相关函数(ACF)、偏自相关函数(PACF)来判别ARMA(p,q)模型的系数和阶数。

若原始时间序列经过判断表现为波动，首先要对时间序列进行差分处理，使其趋于平稳，进行的差分次数就取为d值，最后通过AIC准则、BIC准则确定p、q。ARIMA模型如下。

(1)

式中：Φ(B)=1-φ1B-φ2B2-…φpBp为时间序列ARIMA模型的自回归相关系数多项式；d=(1-B)d为高阶差分；Xt为时间序列；Θ(B)=1-θ1B-θ2B2-…-θqBq为时间序列ARIMA模型的移动平均系数多项式。

1.2 GRU神经网络

循环神经网络(RNN)会受时间序列长度的影响，若输入的时间序列过长，则RNN不能将之前时间步获得的信息传递给当前时刻的时间步。在反向传播期间RNN容易发生梯度爆炸和梯度消失。若RNN的梯度值下降到很小，则获得小梯度的更新层就会停止学习。LSTM神经网络可解决短时记忆的问题，单元结构见图1。LSTM具有门控制单元，门控制单元可以通过权重学习调节信息流，避免梯度下降和梯度爆炸问题。

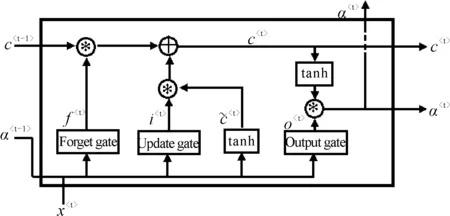
图1 单个LSTM单元结构

LSTM计算公式为

(2)

LSTM的门控单元包含1个Sigmoid神经网络层和1个Pointwise乘法操作。Sigmoid网络层负责描述每个神经元可以通过的信息数量。0代表“任何量禁止通过”，1代表“任何量允许通过”。LSTM门控单元总共分为3步。

第1步,决定从LSTM细胞中丢弃的信息。ft为记忆门(也叫遗忘门)，记忆门读取当前变量xt和前神经元传递的信息at-1，由ft决定丢弃的信息。输出1为“保留”，0为“舍弃”。

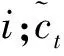
最后确定输出，通过ot(输出门)决定细胞的输出信息，通过ht将信息和通过tanh处理过的细胞状态相乘后输出。

GRU是在LSTM基础上的1种变体，将遗忘门和输入门组合成更新门，见图2。

图2 单个GRU单元结构

与LSTM相比，GRU的结构在简化的同时也保留了长短期记忆网络的能力，这使得GRU的运算效率显著提高。

GRU计算公式为

(3)

式中：ft为更新门，其作用等同于LSTM中的记忆门和输出门，决定细胞状态所存放的新信息以及更新旧的细胞状态；

Γt为重置门，其与LSTM中的ot作用相同，决定细胞的被输出信息。

1.3 注意力机制

注意力机制已经成为了深度学习重要的思想之一，它通常适用于双向循环神经网络，以往的时间序列神经网络只能顺序学习，即对于同一时间步的所有的特征向量等权重学习，结合注意力机制的神经网络在学习过程中计算注意力权重(a set of attention weights)，注意力权重(α(t,t′))代表预测(t)特征向量时(t′)时间步的权重大小。α(t,t′)计算公式如下。

(4)

e(t,t′)由小型神经网络训练获得，见图3。

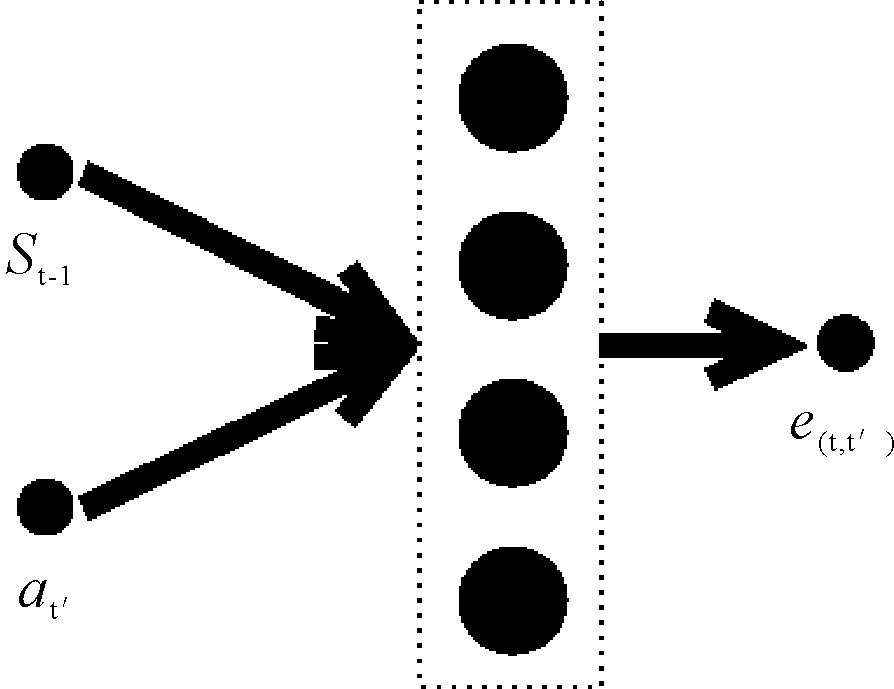
图3 e(t,t′)神经网络

注意力权重通过与(t′)时间步特征向量激活值(αt′)进行加权平均计算得到编码向量C。

(5)

2 组合预测模型

2.1 模型构建

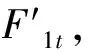
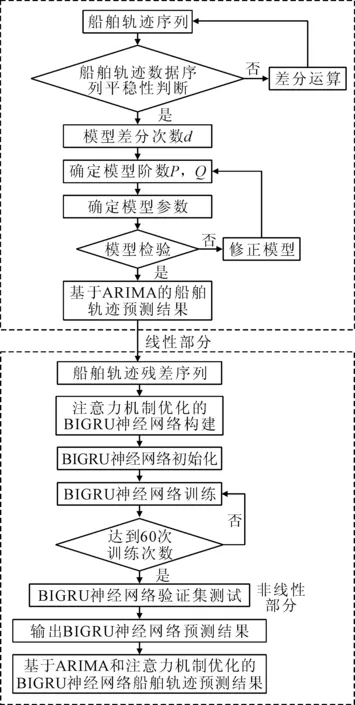
图4 基于ARIMA-BIGRU神经网络残差优化组合预测流程

1)对船舶航迹数据序列进行平稳性检验，确定差分次数d，之后采用AIC(akaike information criterion)准则给模型定阶，以此模型对船舶航迹进行预测，得到船舶航迹的初步预测结果。

2)将ARIMA得到的预测值与船舶航迹真实值Xt比较，计算得出其预测误差et。

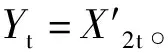
GRU的时间步长即连续n个时刻的船舶航迹数据输入。时间步长过小，神经网络不能很好的学习到输入数据前后的关联性；随着时间步的增大，预测误差呈现下降趋势；当时间步长过长时，输入数据的前后关联性减小，造成网络的预测误差增加。通过保证其他参数不变，更改不同时间步对比预测结果误差，经实验验证在时间步n等于3时预测误差最小。

以t-3～t-1时刻的船舶类型、航向、航速、经度、纬度15个参数作为输入。以t时刻的经度、纬度作为输出。

对于目标船舶，在t时刻的航行状态特征为

Wt=(Var1t、Var2t、Var3t、Var4t、Var5t)

(6)

式中：Var1t、Var2t、Var3t、Var4t、Var5t分别表示t时刻的船舶类型、航向、航速、经度、纬度。

预测当前船舶位置则可以表示为

Et=f(Wt-3、Wt-2、Wt-1)

(7)

式中：Et=(Var4t、Var5t)；f为所训练的模型。

此模型主要由2层BIGRU神经网络层以及1层Dense层组成。其中：α(t,t′)为注意力权重；C为激活值(αt′)与注意力权重α(t,t′)平均加权后的编码向量；St为第t个解码层的隐藏状态，St负责存放第t个预测值yt以及编码向量C的状态，其与(t^')时间步的特征向量的激活值(αt′)通过小型神经网络计算出下一时刻的注意力权重(α(t,t′))。模型结构见图5。

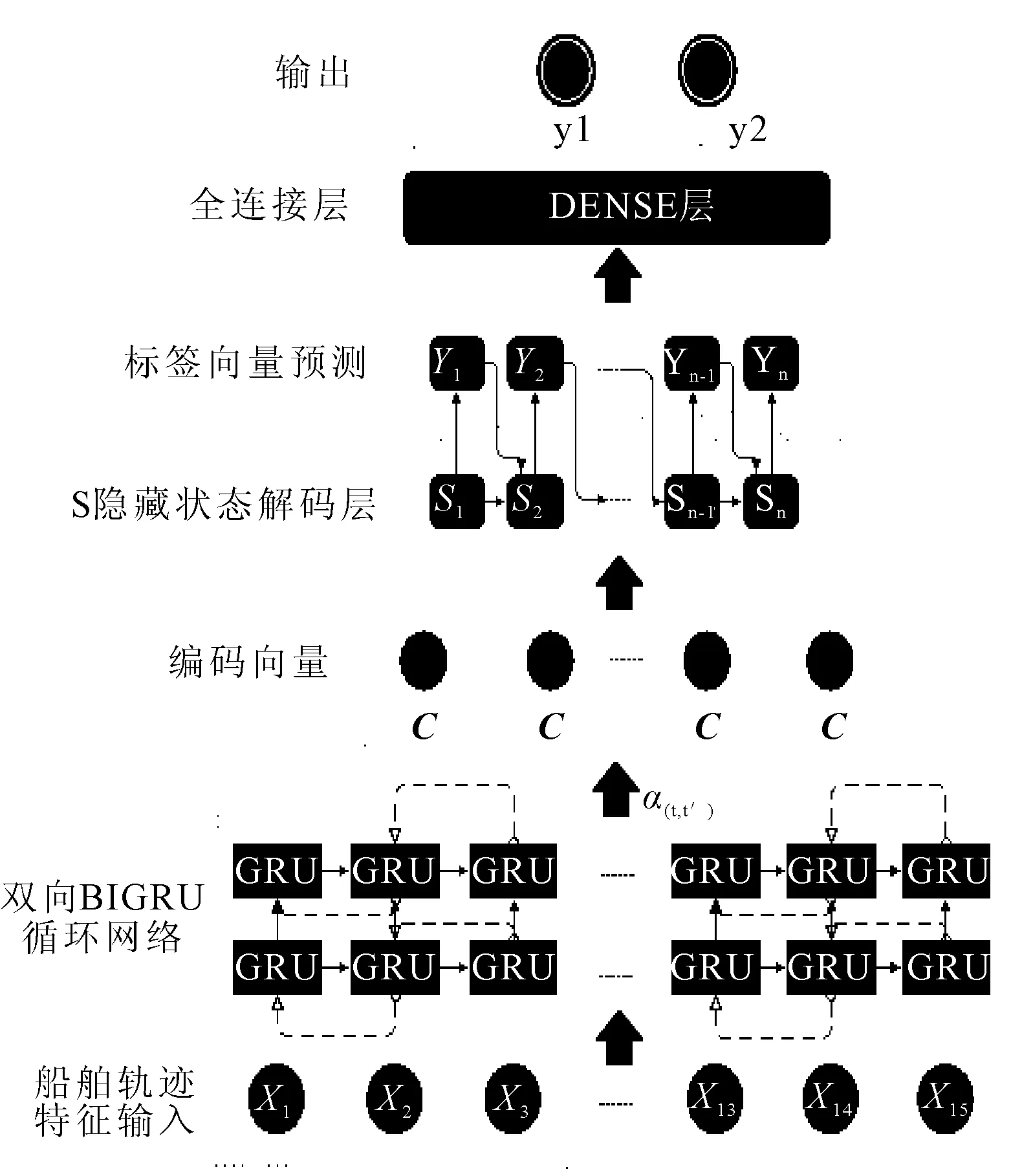
图5 基于注意力机制的BIGRU神经网络模型结构

2.2 预测结果评价指标

为了评价所提出的组合预测方法的合理性和有效性，拟采用与单一预测模型对比均方误差(Mean square error, MSE)、平均绝对误差(mean absolute error, MAE)、均方根误差(root mean square error, RMSE)以及航迹真实值来进行对比分析论证此组合预测方法的有效性。

3 实验验证

3.1 数据来源

实验数据采用卡里蒙群岛2019年6月3—22日的47 326条AIS数据。考虑到输入的数据是多种类型船舶的AIS数据集，不同类型船舶AIS数据中蕴含的航行规律不同，所以将船舶类型作为参数输入时，神经网络能够区分船舶类型特征来分类挖掘规律，相较于直接输入大量AIS数据效果要好。主要选取船型(shiptype)、航向(course)、航速(speed)、经度(lon)、纬度(lat)5个特征值。

3.2 数据分析与预处理

原始的AIS数据存在大量的特征数据，需要进行数据预处理，首先将船舶类型(ship type)转换成由1开始的数字型标签，将经纬度转换成以秒(t)为单位的浮点数。若数据缺失，则采用以下方法进行修复。

1)将数据依据特征值等量的分为不同组，若某一特征值组内在这一组所有值的平均值3倍以上，则判断为异常点。

2)使用三次样条插值法进行异常点剔除，以保证数据时间间隔相同，选取当前点x前后2点，提取x时间ti、ti+1船舶经纬度为(xi，yi)、(xi+1，yi+1)，t时刻的船舶经纬度可以用式(8)计算。

(8)

式中：hi=xi-xi-1；Mi为插值函数X(t)在节点ti处的二阶导数。

3)使用三次样条插值法对修复后的数据进行插值，获得时间间隔为10 s的数据。

最后将船型、航向、航速，以及ARIMA输出的经度残差(lon-res)、纬度残差(lat-res)以时间为索引，以(t-3)～(t-1)时刻的15个值作为特征值输入，t时刻的经度残差和纬度残差作为预测标签参照，处理完毕后将数据做离差标准化(min-max normalization)归一化处理。

3.3 模型训练与预测

1)模型参数初始化。通过网格搜索法进行参数寻优，确定模型拟采用3层神经网络结构，其中前两层为循环BIGRU神经网络层，第三层为Dense层。每层的神经单元个数分别为50、128、2。训练次数为60次，mini-batch数目为128。梯度下降方式采用adam下降方法。

2)模型训练。将所有数据分成训练集和测试集，其中训练集数据为4/5，测试集测试数据为1/5。BIGRU网络的输入为时间序列，输入参数x1～x15为：Wt-3、Wt-2、Wt-1。

3)模型预测。将测试集输入到训练集训练好的模型中进行预测，同时要对预测数据进行反归一化处理，使得预测得到的数据是真实的经纬度数据。

3.4 实验结果

测试集在训练集训练后的神经网络模型上依据经度、纬度2个特征计算出MSE、MAE、RMSE，实验结果见图6～8。

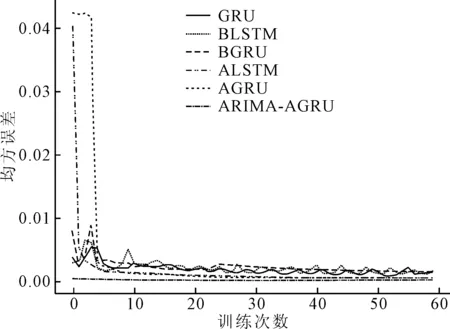
图6 测试集MSE

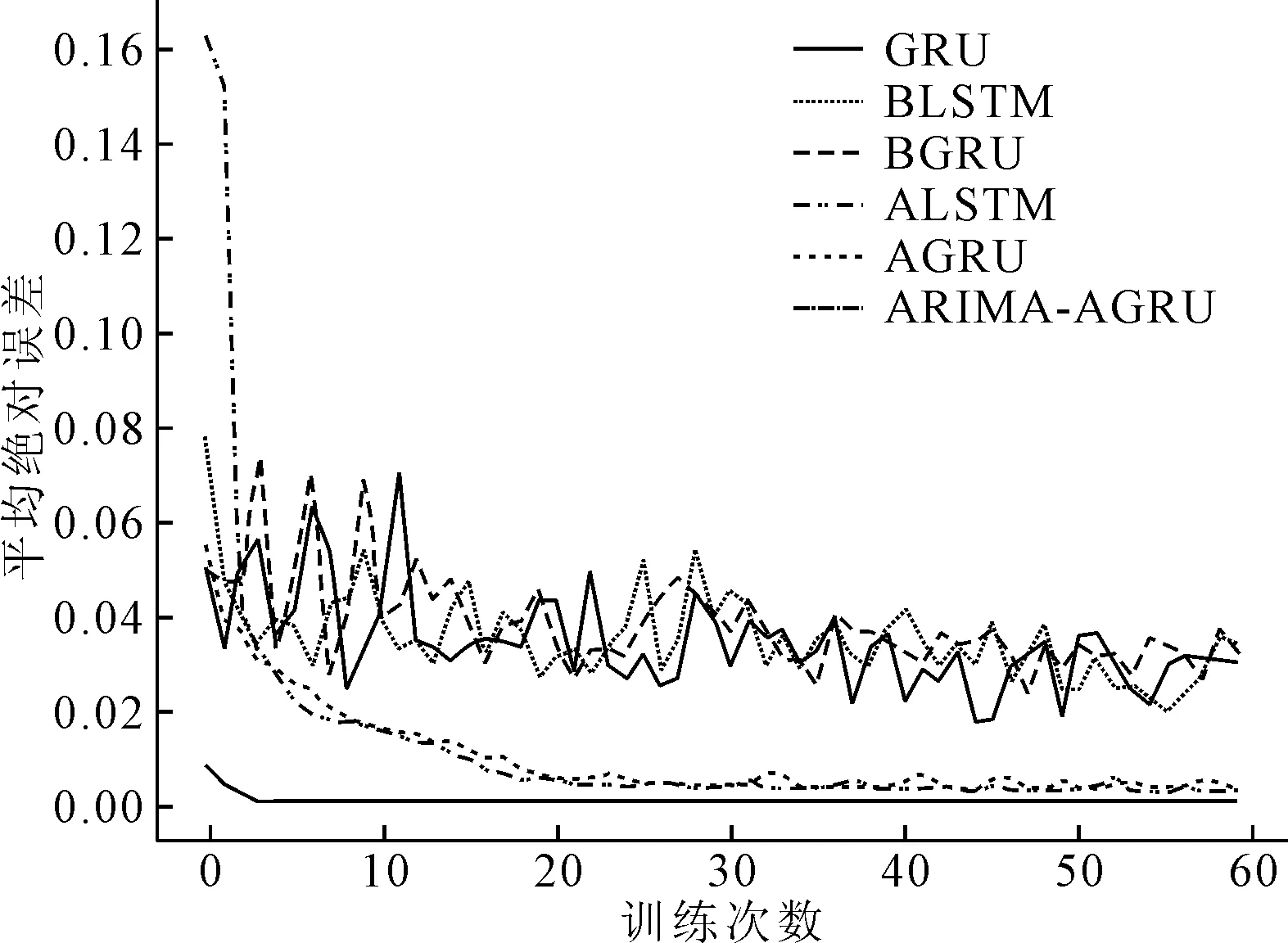
图7 测试集MAE

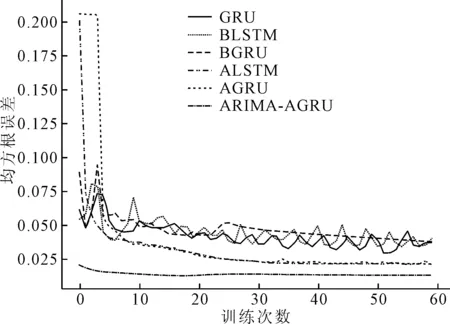
图8 测试集RMSE

由以图6～8可知，GRU的误差精度优于LSTM。单向GRU模型与双向GRU模型对比MSE、MAE、RMSE分别降低8.024 8×10-4、3.52×10-3、9.999 05×10-3。结合注意力机制后BIGRU三种误差相较于BIGRU分别都有降低，未结合注意力机制的训练模型训练误差波动较大，BIGRU、BLSTM在结合注意力机制优化后误差精度和平稳性均优于BIGRU、BLSTM。结合注意力机制的ARIMA-BIGUR模型的预测效果最好、预测精度最高。通过对比误差指标可知基于ARIMA和注意力机制的BIGRU循环神经网络组合预测模型，在MSE、MAE、RMSE预测指标上相较于其它5种模型有较大的提升。

用模型对80个航迹点进行预测，结果见图9、10。

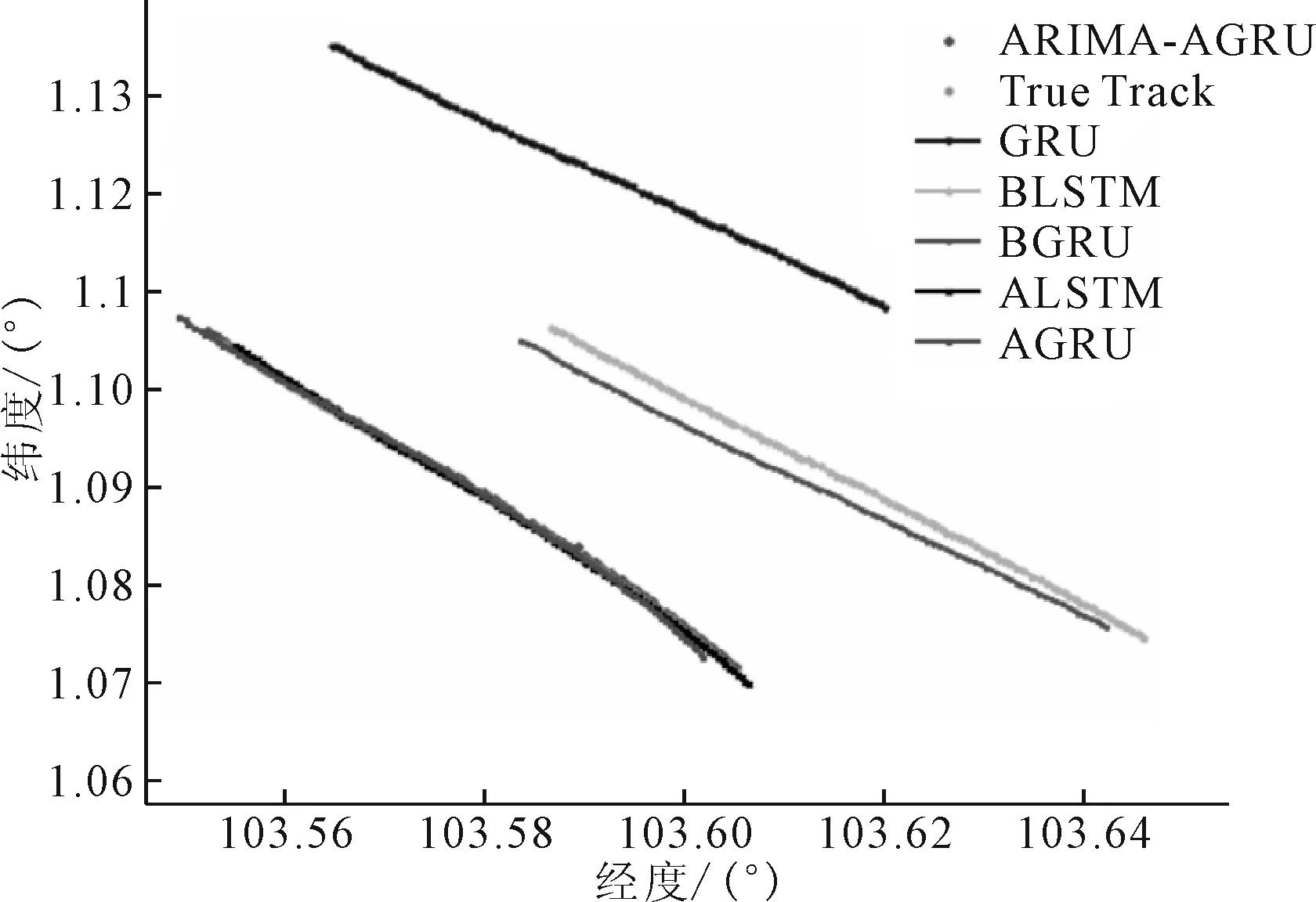
图9 航迹预测对比

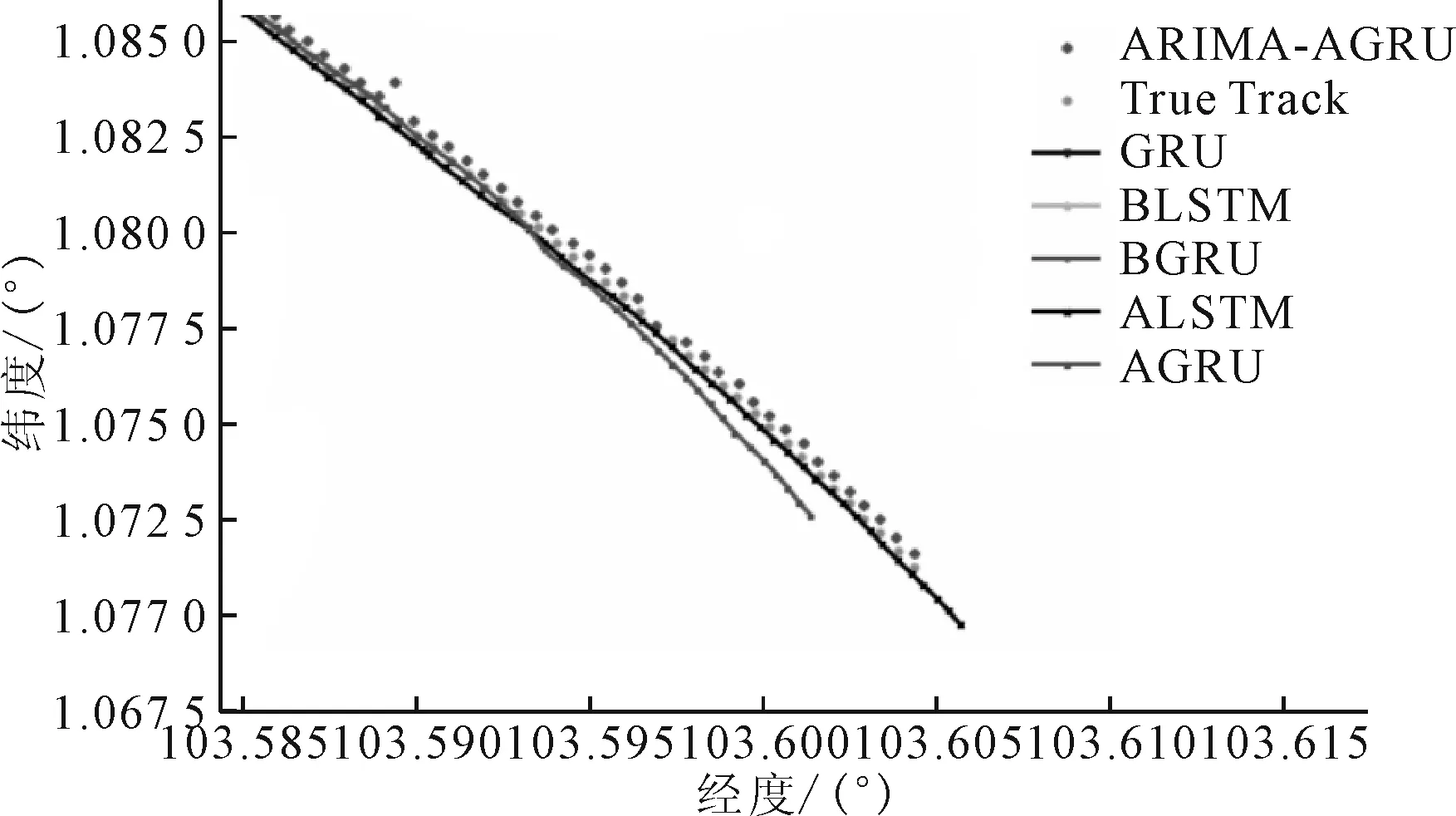
图10 放大后的航迹预测对比

对比真实的船舶航迹可以发现，未经过注意力机制优化的GRU、BIGRU、BLSTM与真实航迹相比有很大的偏差，经过注意力机制优化的BIGRU、BLSTM预测效果与真实值接近，同时结合ARIMA与注意力机制的BIGRU模型的预测效果与真实航迹十分吻合，说明本文预测方法能够进一步提升航迹预测精确度。

4 结论

相较于传统预测方法，基于ARIMA-BIGRU的组合预测模型具有更高的精确度和平稳性。利用ARIMA进行线性预测可以将航迹数据处理的更加平稳；利用BIGRU结合注意力机制对残差进行优化，能够挖掘出非线性因素对航迹造成的影响，从而准确预测出船舶轨迹。未来的研究应考虑模型的在线更新和实时预测，以进一步提高模型的航迹预测能力。