圆角化方形截面高层建筑风荷载特性试验
2016-07-28李秋胜周亚萍李建成李毅
李秋胜+周亚萍+李建成+李毅

摘要:对圆角率为25%的正方形高层建筑刚性模型进行了测压试验,并对其风荷载特性进行了研究;分析了三分力系数和基底力矩系数随风向角的变化规律,给出了阻力系数平均值、根方差值和升力系数根方差值拟合结果;分析了最不利风向角下的风荷载功率谱,并采用经验公式进行拟合;分析了体型系数并与规范中正方形体型系数进行了对比。结果表明:对正方形建筑角部进行圆角化处理能明显降低建筑风荷载,且消除了功率谱曲线谱峰尖而窄的单峰现象,从本质上改变风荷载特性,有利于主体结构的抗风设计;角部区域负压较大,对幕墙抗风设计不利。
关键词:高层建筑;方形截面;风洞试验;三分力系数;风荷载功率谱;体型系数
中图分类号:TU973.2文献标志码:A
Abstract: The pressure test was carried out on the rigid model of square section highrise building with round corner rate of 25%, and the characteristics of wind loads were studied. The change rules of threecomponent coefficient and base moment coefficient along with the wind angle were analyzed. The fitting results of mean value of drag coefficient, root square deviation of drag coefficient and lift coefficient were given. The wind load power spectrum under the most unfavorable wind angle was analyzed, and fitted by empirical formula. The shape coefficient was analyzed and compared with the square shape coefficient of code. The results show that the wind load can be significantly reduced when the corners of square building are rounded, and the sharp and narrow single peak phenomenon of the power spectrum curve can be eliminated. The wind load characteristic is changed in essence, and is beneficial for the wind resistant design of the main structure. The negative pressure in the corner area is larger, which is disadvantageous to the wind resistance design of curtain wall.
Key words: highrise building; square section; wind tunnel test; threecomponent coefficient; wind load power spectrum; shape coefficient
0引言
不同截面形状的高层建筑风压分布特性、风荷载特性会明显不同[16]。对于正方形建筑和矩形建筑,适当的局部修正能明显改变高层建筑的风压分布特性和风荷载特性。Carassale等[7]的研究表明,圆角处理措施使气流分离之后更易再附着于模型的2个侧面。Tamura等[8]的研究表明,切角和凹角处理能影响方柱的尾流宽度,能明显降低模型的阻力。此外,圆角处理导致分离剪切层有可能再附于模型的2个侧面,影响模型的风压特性。Melbourne等[9]研究了凹角、切角、圆角这3种不同角部修正方式对方形截面高层建筑横风向气动力的影响,认为适当的角部修正率可使横风向气动力谱的峰值大幅减小,从而降低临近涡激共振风速下结构的风致响应。可见,圆角处理措施会影响气流分离和再附着,导致模型气动特性、风荷载及风致响应的改变。本文基于刚性模型测压试验,分析了圆角率为25%的正方形截面高层建筑风荷载三分力系数和功率谱特性,计算其体型系数,以供抗风设计参考。
1风洞试验概况
风洞试验在湖南大学建筑与环境风洞实验室中进行,试验模型为ABS板制作的刚性模型,模型尺寸为100 mm×100 mm×600 mm,缩尺比为1∶500,测点布置和风向角定义如图1所示(图1中,FD,FT,FL分别为阻力、升力和扭矩),风向角间隔为5°,逆时针为正,由于模型的对称性,试验范围为0°~90°;高层建筑所处的环境一般为C类地貌,本文试验采用挡板、尖劈和粗糙元调试得到C类风场,试验风速为10 m·s-1。
图2为各测点层阻力系数平均值CD和根方差值C′D随风向角的变化趋势。从图2中可以看出,由于模型本身的对称性,阻力系数的平均值和根方差值均关于45°风向角对称,且各层变化趋势一致,均随风向角先增大后减小。阻力系数的平均值在全风向角下的变化范围为0.32~1.0,最大值出现在35°风向角(由于模型的对称性,只讨论0°~45°风向角范围,下同),最小值出现在0°风向角。文献[10]中正方形截面高层建筑的层阻力系数平均值全风向角下变化范围大致为0.7~1.3,高于本文结果,可见圆角化处理能降低顺风向平均风荷载。阻力系数的根方差值在全风向角下的变化范围为0.11~0.22,最大值出现在15°风向角,最小值出现在0°风向角。文献[11]中正方形截面高层建筑的层阻力系数根方差值全风向角下变化范围大致为0.28~0.36,故圆角化处理能降低顺风向脉动风荷载。可见,圆角化处理能同时降低顺风向平均荷载和脉动荷载;圆角化处理之后,层阻力系数的平均值和根方差值的最大值分别出现在35°和15°风向角。
图3为各风向角下层阻力系数平均值和根方差值随高度z的变化趋势,其中H为模型高度。从图3中可以看出:层阻力系数平均值沿高度表现出增大的趋势,在顶部受三维绕流的影响,出现局部减图3层阻力系数随高度的变化小;整体而言,与2α(α为地面粗糙度指数)指数率有一定区别,因为迎风面风压沿高度与2α指数率接近,但背风面风压沿高度变化较小。阻力系数平均值的最大值约出现在模型的0.85H处。阻力系数根方差值沿高度变化不大。
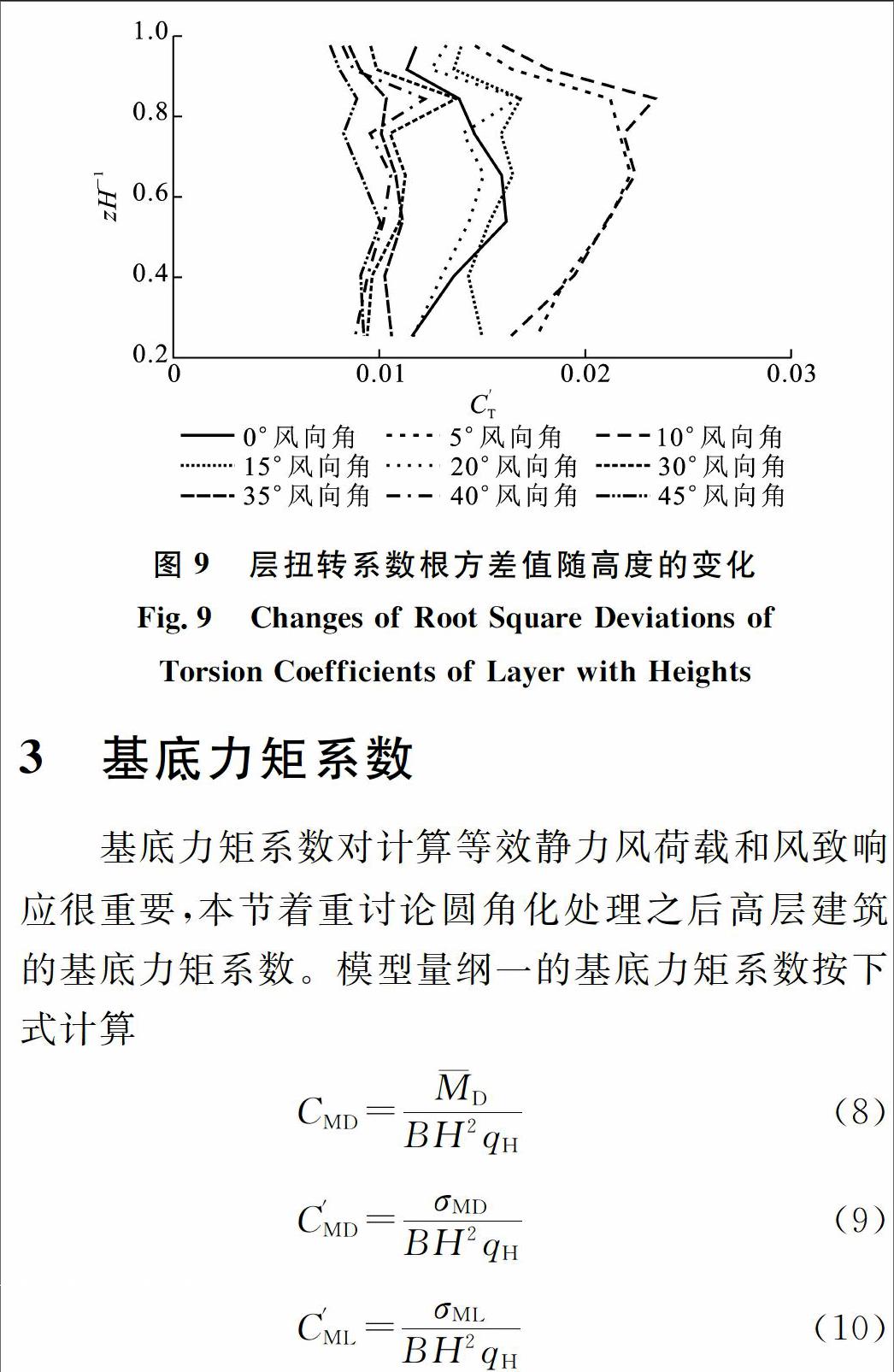
图5为各测点层升力系数根方差值C′L随风向角的变化趋势。升力系数根方差值在全风向角下的变化范围为0.11~0.32,文献[11]中正方形截面高层建筑层升力系数根方差值在全风向角下的变化范围为0.12~0.45,故圆角化处理能明显降低横风向脉动风荷载。文献[13]中指出,当高层建筑的高宽比大于4时,其横风向风振响应为结构设计的控制性因素,由此可知圆角化处理对高层建筑的主体结构抗风设计有利。升力系数根方差值的最大值出现在5°风向角,在来流和模型对称轴接近时(0°和45°风向角),升力系数根方差值较小,最小值出现在45°风向角。由此可见,圆角化处理有利于高层建筑的抗风设计,层升力系数的最不利风向角为5°。
图6为层升力系数根方差值C′L随高度的变化趋势。升力系数受来流湍流、截面外形、漩涡脱落的共同影响,因而其根方差值沿高度的变化规律与阻力系数沿高度的变化规律明显不同。0°~20°风向角范围内(包括最不利风向角5°)层升力系数根方差值沿高度先增大后减小,最大值出现在0.6H~0.7H;30°~45°风向角范围内层升力系数根方差值沿高度逐渐减小。
通过试算发现,圆角化处理消除了最不利风向角下功率谱曲线谱峰尖而窄的单峰现象,功率谱相对平坦,峰值带宽较大,但在30°风向角以后功率谱曲线也出现了明显的谱峰尖而窄的单峰现象;通过前面的三分力系数和基底力矩系数分析可知,在全风向角下其变化并不是很大,如果某风向角下脉动根方差比最不利风向角略小,但当其荷载功率谱的谱峰值对应的频率与结构本身频率接近时,则此风向角下的风致响应可能会不利;鉴于此,图15给出35°风向角下横风向风荷载功率谱和文献[12],[16],[17]的拟合结果,供工程设计人员根据结构本身动力特性选择式(15)或式(16),(17)。由图15可知,功率谱曲线在略大于0.1 Hz处出现峰值,文献[17]公式在高频部分很吻合,但在低频部分偏低,文献[12],[16]模型拟合效果较好,文献[16]对低频的拟合更吻合,给出文献[16]公式的参数拟合结果:
由图15可见,各层拟合结果和基底拟合结果很接近。由拟合结果知,正方形高层建筑角部圆角化处理之后,当角部处于迎风面时,斯托罗哈数为0.118。
4.3扭转向风荷载功率谱
由基底弯矩力矩分析可知基底扭矩根方差系数相对于基底弯矩根方差系数较小,但考虑到扭转风致响应会放大建筑角部区域的位移和加速度,本节给出扭转向风荷载功率谱(图16)。层扭矩功率谱和基底扭矩功率谱曲线整体随折算频率的变化趋势是一致的,且层扭矩功率谱和基底扭矩功率谱曲线都出现了2个峰值,与宽厚比大于1的矩形建筑类似。鉴于功率谱曲线的特点,选用文献[16]提出的三分量和公式,先试算以确定部分参数,然后再拟合得到其他参数,由于不同高度扭矩功率谱吻合并不是很好,参数拟合结果变化较大。下面给出基底扭矩功率谱的拟合结果以供参考,即
表1为典型测点层的体型系数。体型系数在正面和侧面沿高度变化较大,靠近底部和顶部处变化较明显,体型系数呈现出上小下大的特点,与文献[18],[19]的结论一致;背风面体型系数沿高度先减小再增大,呈抛物线形变化,整体变化不大。迎风面最大局部体型系数为1.1,侧风面上风向最大局部体型系数为-2.06,侧风面下风向最大局部体型系数为-0.82,背风面最大局部体型系数-0.52,最大值均出现在模型底部H层;《建筑结构荷载规范》[20]中正方形建筑迎风面局部体型系数为1.0,侧风面上风向局部体型系数为-1.4,侧风面下风向局部体型系数为-1.0,背风面局部体型系数为-0.6。可见,圆角化处理后,迎风面和背风面的局部体型系数变化不大,但侧风面上风向局部体型系数均比规范中正方形角部区域局部体系系数大,增大幅度也很大,最多增大1.5倍。由图17可知,侧风面上风向局部体型系数偏大的测点区域面积较大,故圆角化处理对部分幕墙抗风设计是不利的,设计时应注意。
6结语
(1)分析了三分力系数随风向角的变化,与阻力相比,升力和扭矩对总静荷载的贡献比较小,可以忽略。圆角化处理后的三分力系数均比相同工况下的正方形建筑的三分力系数小,可见圆角化处理有利于高层建筑主体结构的抗风设计。基底力矩系数与三分力系数随风向角的变化规律一致。
(2)分析了三分力系数随高度的变化,层阻力系数平均值沿高度与2α指数率有一定区别,选用线性模型拟合阻力系数。升力系数平均值和根方差值沿高度的变化规律与阻力系数沿高度的变化规律明显不同,选用多项式模型拟合升力系数根方差值。
(3)顺风向基底弯矩功率谱在低频段和层阻力功率谱吻合较好,在高频段低于层阻力功率谱,分别给出了层阻力功率谱和基底弯矩功率谱的数学模型拟合结果;最不利风向角下横风向基底弯矩功率谱和层升力功率谱吻合较好,鉴于此,采用四参数模型给出了层升力功率谱和基底弯矩功率谱的整体拟合结果;与矩形建筑相比,圆角化处理消除了最不利风向角下功率谱曲线谱峰尖而窄的单峰现象,说明圆角化处理从本质上改变了建筑的横风向荷载;在30°风向角以后功率谱曲线出现了明显的谱峰尖而窄的单峰现象,鉴于此,给出了35°风向角下横风向风荷载功率谱及拟合结果,供工程设计人员根据结构本身动力特性选择。
(4)圆角处理后,侧风面上风向局部体型系数均比规范中正方形角部区域局部体型系数大,增大幅度也很大,最多增大1.5倍,故圆角化处理对部分幕墙抗风设计是不利的,设计时应注意。
参考文献:
References:
[1]李永贵,李秋胜,戴益民.开洞高层建筑风荷载的试验研究[J].振动与冲击,2015,34(11):6367.
LI Yonggui,LI Qiusheng,DAI Yimin.Tests for Wind Load of Tall Buildings with Openings[J].Journal of Vibration and Shock,2015,34(11):6367.
[2]李永贵,李秋胜,戴益民.矩形截面高层建筑扭转向脉动风荷载数学模型[J].工程力学,2015,32(6):177182.
LI Yonggui,LI Qiusheng,DAI Yimin.Mathematical Models for Torsional Fluctuating Wind Loads on Rectangular Tall Buildings[J].Engineering Mechanics,2015,32(6):177182.
[3]郑朝荣,任凯,武岳,等.上部吸气控制下超高层建筑的平均风荷载特性研究[J].武汉理工大学学报,2015,37(6):6065.
ZHENG Chaorong,REN Kai,WU Yue,et al.Experimental Research on the Characteristics of Mean Wind Loads of Highrise Buildings Controlled by Uppersurface Suction[J].Journal of Wuhan University of Technology,2015,37(6):6065.
[4]邹鑫,汪之松,李正良.稳态冲击风作用下高层建筑风荷载特性试验研究[J].湖南大学学报:自然科学版,2016,43(1):2936.
ZOU Xin,WANG Zhisong,LI Zhengliang.Experimental Study on the Wind Load Characteristics of Highrise Building in Stationary Downbursts[J].Journal of Hunan University:Natural Sciences,2016,43(1):2936.
[5]赵昕,王立林,郑毅敏.超高层建筑结构组合调谐风振控制系统[J].同济大学学报:自然科学版,2016,44(4):550558.
ZHAO Xin,WANG Lilin,ZHENG Yimin.Combined Tuned Damperbased Windinduced Vibration Control for Super Tall Buildings[J].Journal of Tongji University:Natural Science,2016,44(4):550558.
[6]钟振宇,楼文娟.基于风重耦合效应超高层建筑顺风向等效静力风荷载[J].工程力学,2016,33(5):7481.
ZHONG Zhenyu,LOU Wenjuan.Equivalent Static Wind Load on Extrahigh Buildings Along Wind Based on Windgravity Coupling Effect[J].Engineering Mechanics,2016,33(5):7481.
[7]CARASSALE L,FREDA A,MARREBRUNENGHI M.Experimental Investigation on the Aerodynamic Behavior of Square Cylinders with Rounded Corners[J].Journal of Fluids and Structures,2014,44:195204.
[8]TAMURA T,MIYAGI T,KITAGISHI T.Numerical Prediction of Unsteady Pressures on a Square Cylinder with Various Corner Shapes[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,7476:531542.
[9]MELBOURNE W H,CHEUNG J C K.Designing for Serviceable Accelerations in Tall Buildings[C]//World Scientific.Proceeding of the 4th International Conference on Tall Buildings.Singapore:World Scientific,1988:148155.
[10]钱涛.不同长宽比矩形截面高层建筑的风荷载研究[D].杭州:浙江大学,2013.
QIAN Tao.Study of Wind Loads on Highrise Building with Different Length to Width Ratios[D].Hangzhou:Zhejiang University,2013.
[11]全涌.超高层建筑横风向风荷载及响应研究[D].上海:同济大学,2002.
QUAN Yong.Acrosswind Loads and Responses on Super Highrise Buildings[D].Shanghai:Tongji University,2002.
