量子中继过程中纠缠态的选择*

石韬 吕丽花 李有泉

(浙江大学物理系,杭州 310027)

实现量子中继的关键是克服量子储存器中纠缠态的退相干问题.目前,人们常用半导体量子点中的电子自旋来构建纠缠态从而实现量子中继过程.在该过程中,两个半导体量子点之间相距很远,可以认为它们之间没有相互作用.因此,量子点内电子自旋与它周围的核自旋之间的超精细相互作用被认为是导致系统退相干的最重要原因之一.在以前的相关工作中,人们通常将核自旋对电子自旋的超精细相互作用视为一个大小和方向都是随机的并且满足高斯分布的等效磁场.本文在考虑核自旋的等效磁场以及外加磁场的情况下,研究了两个量子点中继系统的退相干问题.首先利用数值方法分别计算了4 组Bell 基随时间的演化规律,发现当外加磁场增大到一定值时,4 组Bell 基被分为两类.体系不可能通过时间演化从一类Bell 基跃迁到另一类Bell 基,而只能在同类的两个Bell 基之间相互跃迁.这有效提高了系统的保真度,并且抑制了核自旋对体系纠缠态的影响,从而抑制退相干.其次,对于给定的较大外加磁场,采用解析方法研究了核自旋涨落对纠缠态的影响,给出了初态保真度及退相干时间的解析形式.发现对于相同的核自旋涨落,4 组Bell 基的退相干时间相同,但是两类Bell 基随时间演化的规律不同,其中一类的保真度在指数衰减的同时伴随快速周期性振荡,不便于操控.期望本文的研究能对量子中继过程中纠缠态的选择问题提供理论支持和建议.

1 引言

在量子信息传输过程中,最重要的是在通信线路的两个节点上成功发送一对纠缠态.每一对纠缠态可以作为一个量子传输通道,进行量子信息的远程传输[1,2].目前光子纠缠态是量子通信中唯一可以远距离飞行的纠缠态[3-6],然而单个光子在商用光纤中光强和极化都以0.2 dB/km[7,8]的速率衰减,这意味着商用光纤有效传输长度仅有80—120 km[7,8].因此,为了增加量子传输通道距离,一种方法是将量子传输通道分为好多节,每一节长度在120 km内,同时在两个节点之间放置一个包含两个量子储存器[9]的量子中继器[10],如图1(a)所示.在量子中继器中,量子储存器将光子的纠缠态储存为电子自旋的纠缠态[11-13].

通常有3 种利用光子干涉和探测将光子纠缠态交换到电子自旋纠缠态的方案,分别为EPR(Einstein-PodolskyRosen)方案[8]、Hybrid 方案[14]和DLCZ (Duan-Lukin-Cirac-Zoller)方案[15].DLCZ方案由段路明等[15]提出,根据探测光子数不同,该方案可以分为单光子探测方案和双光子探测方案.与其他两个方案相比,DLCZ 方案最大的优点是不需要制备复杂的纠缠源,只需要制备符合要求的量子储存器,因而成为量子中继的主流之一.在每个节点的量子中继器上,利用纠缠态交换(quantum swapping)技术[14-17],可以逐步建立Alice 与 Bob之间的量子远程传输通道[1,18],如图1(b)和图1(c)所示.能够作为量子存储器的系统,其储存的纠缠态要有较长的退相干时间.目前许多系统,例如原子系综[8,15]、半导体量子点[12,19,20]、超导电路[21,22]等,都可以用来做量子储存器.以GaAs 或者Si 半导体量子点为例,它们通过两个量子点中电子自旋的纠缠态来储存量子信息[19,23].众所周知,对于两个电子自旋系统,可以选用4 个最大纠缠态(即4 个Bell 基)为一组正交完备基矢来描述体系的状态[17].如果体系在初始时刻处于某一个Bell基上,由于核自旋对电子自旋的超精细相互作用,随着时间的演化,体系会有一定概率从初始时刻所处的Bell 基跃迁到其他Bell 基上,从而导致了纠缠态的退相干[13,19,24-26].为研究核自旋引起的纠缠态的退相干问题,有文献将核自旋对电子自旋的超精细相互作用等效为一个大小和方向都是随机的等效磁场.该磁场满足高斯分布[24,25,27],被命名为Overhauser 场[19,24,25,28].本文同时考虑核自旋及外加磁场对电子自旋的相互作用,研究了系统纠缠态的退相干问题.通过数值和解析方法,分别计算了体系状态随时间的演化,发现较大的外加磁场可以抑制电子自旋向上和自旋向下状态间的反转,从而抑制了某些Bell 基间的相互跃迁.据此将4 个Bell 基分为两类,每一类中包含两个Bell 基.只有在同类的两个Bell 基之间存在相互跃迁,而不同类Bell 基之间不能相互跃迁,这在一定程度上抑制了系统纠缠态的退相干.对于给定的外加磁场,研究了核自旋涨落对纠缠态的退相干的影响.发现对于相同的核自旋涨落,两类Bell基的退相干时间相同,但是两类Bell 基随时间的演化规律不同,其中一类Bell 基的保真度在指数衰减的同时伴随快速周期性振荡,不便于操控,因此在量子中继过程中不建议选择.

2 等效磁场与理论模型

2.1 超精细相互作用和等效磁场

在半导体量子点,如GaAs 中,电子自旋与它周围核自旋的超精细相互作用可以写成[25]

其中ψ(Rj)是第j个核自旋附近电子的包络波函数,求和是对晶格中所有核自旋求和;ν0是晶胞的体积;S是电子自旋算符;µ0是玻尔磁子;µj,Ij,Rj分别对应核子磁矩、核自旋和第j个核自旋的位置,uc(Rj)是第j个核自旋附近电子的Bloch 波函数.将哈密顿量(1)关于核子的系综进行平均,得到等效哈密顿量如下:

以GaAs 量子点为例,实验所施加外磁场通常0.2 T 左右[19,24,28].核自旋的Zeeman 能量ωn对应的温度大约在mK 量级[28],核自旋对电子自旋的相互作用对应的温度在nK 量级[19,28],而系统所处温度在K 量级[18,28],因此可以认为热涨落使体系中所有核自旋杂乱无序.这样等效磁场BN各向同性,在任意一个方向,比如z方向,其磁场大小可以用高斯分布来表示[25]:

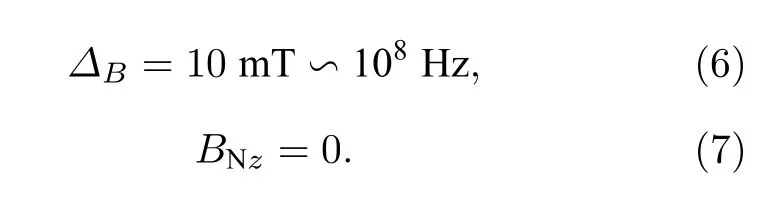
同理,可以得到另外两个方向上等效磁场的高斯分布形式[25]:

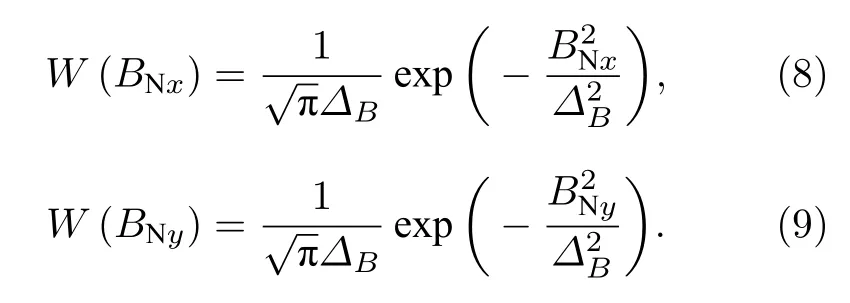
2.2 理论模型

在量子中继中,组成最大纠缠态(4 个Bell 基)的两个电子自旋分别储存在相距80 km 的两个GaAs 量子储存器中,如图2所示.由于两个量子储存器相距很远,它们之间的相互作用可以忽略,因此电子自旋只感受到外加磁场及周围核自旋产生的等效磁场的相互作用,系统的哈密顿量如下:

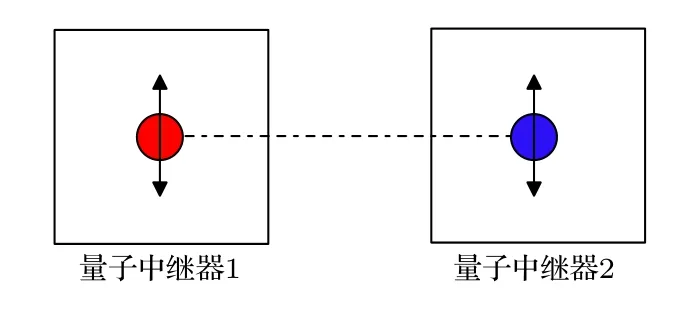
图2 两个相互纠缠的量子中继器,纠缠态为两个电子自旋组成的4 个Bell 基.Fig.2.Entanglement of the two separated quantum repeaters.Entangled states are the four Bell states constructed by two electron spins.

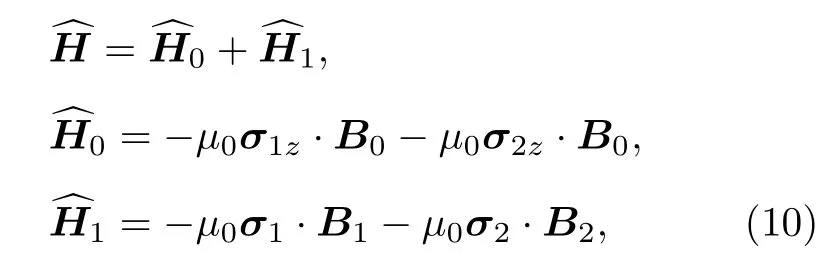
两个电子自旋组成的4 个Bell 基为

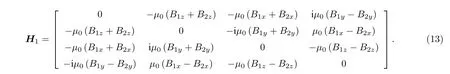
B1z和B2z的大小满足高斯分布且相互独立,两个相互独立的高斯分布相加或者相减也是高斯分布[27].

既然B1和B2在3 个方向上的磁场大小相同,满足相同的高斯分布,因此可以将H1化简为

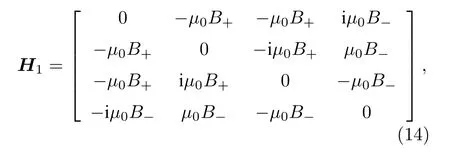
其中B+=B1x(yz)+B2x(yz),B-=B1x(yz)-B2x(yz),B+和B-也满足高斯分布,即

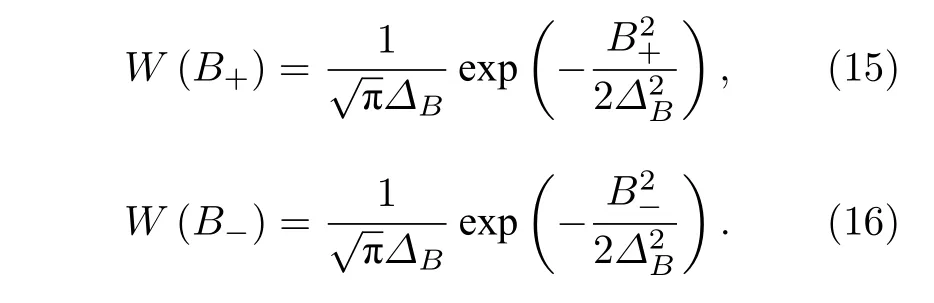
3 数值结果与分析

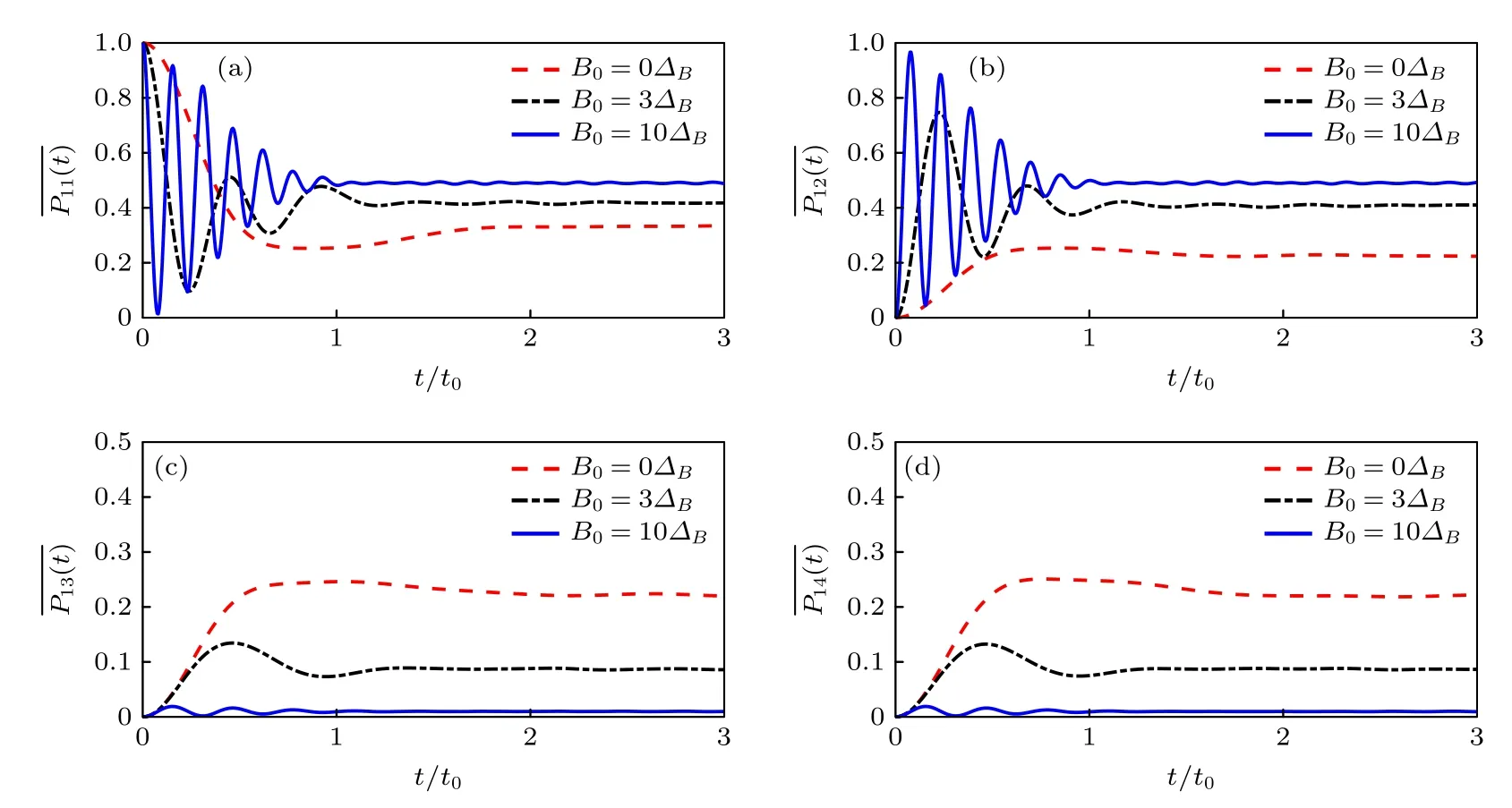
图33 种不同大小的外加磁场下,体系处于4 个不同Bell 基上的几率随时间的演化规律 (a),(b),(c),(d)分别对应系统处于|〉,|〉 ,|〉,|〉的平均几率.体系初态为 〉,外加磁场参数为 B0=0(红色虚线),B0=3ΔB (黑色点划线),B0=10ΔB(蓝色实线).时间以 t0=1/(µ0ΔB) 为单位Fig.3.Time evolution of mean probability in four Bell states:(a) 〉,(b) 〉,(c) 〉,(d) 〉 for different applied magnetic fields.The initial state is 〉,and the parameters are B0=0(red dash line),B0=3ΔB (black dash dot line),B0=10ΔB(blue solid line).Time is in the unit of t0=1/(µ0ΔB).

图43 种不同大小的外加磁场下,体系处于4 个不同Bell 基上的几率随时间的演化规律 (a),(b),(c),(d)分别对应系统处于〉,〉 ,〉,〉的平均几率.体系的初态为〉,外加磁场参数为 B0=0(红色虚线),B0=3ΔB (黑色点划线)、B0=10ΔB(蓝色实线).时间以 t0=1/(µ0ΔB) 为单位Fig.4.Time evolution of mean probability in four Bell states:(a) 〉,(b) 〉,(c) 〉,(d) 〉 for different applied magnetic fields.The initial state is 〉,and the parameters are B0=0(red dash line),B0=3ΔB (black dash dot line),B0=10ΔB(blue solid line).Time is in the unit of t0=1/(µ0ΔB).

4 解析结果与分析

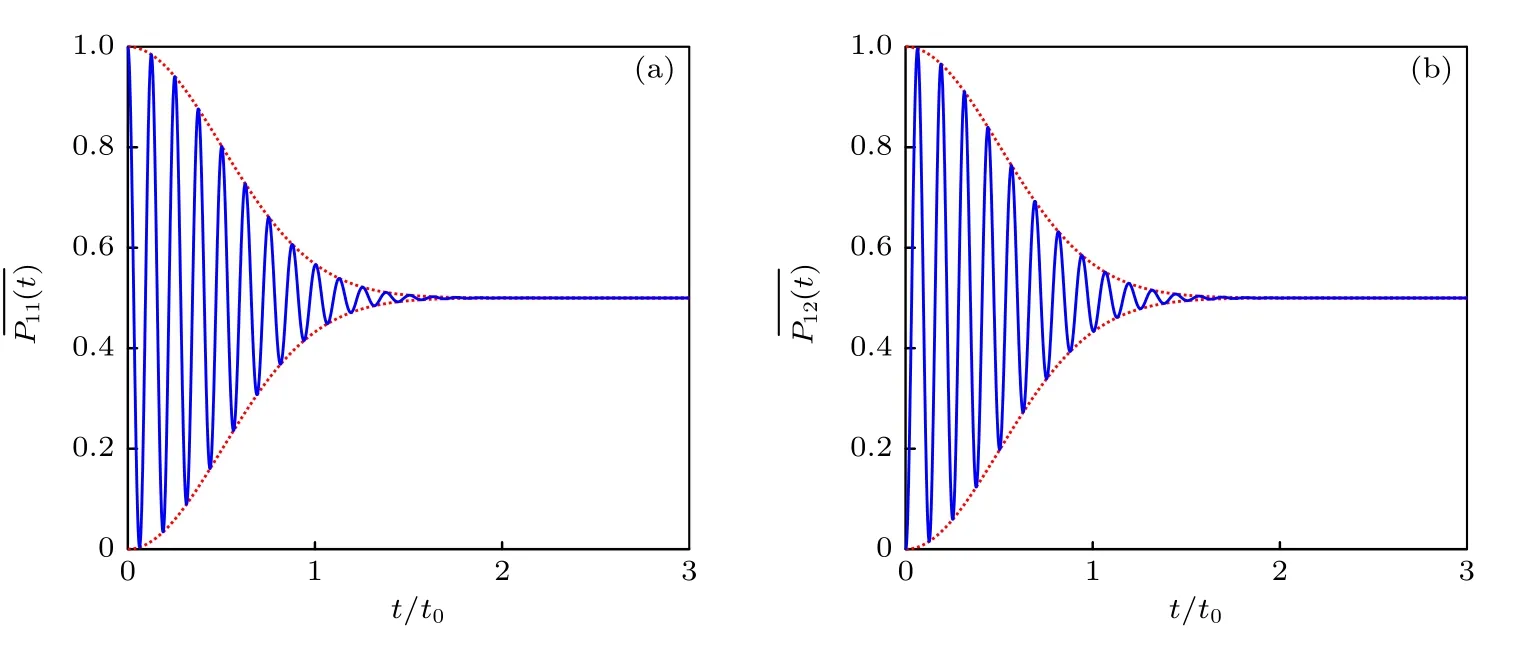
图5 (a)系统仍然处在〉上的平均几率随时间的演化;(b)系统跃迁到〉的平均几率随时间的演化.系统初态为〉,时间以 t0=1/(µ0ΔB) 为单位Fig.5.(a) Time evolution of the mean probability in 〉,(b) that in 〉.The initial state is ,and the time is in the unit of t0=1/(µ0ΔB).

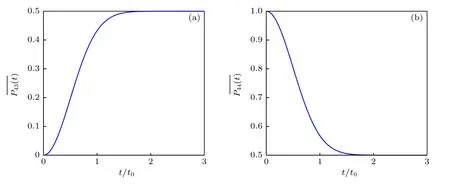
图6 (a)系统仍然处在〉上的平均几率随时间的演化;(b)系统跃迁到〉的平均几率随时间的演化.系统初态为〉,时间以 t0=1/(µ0ΔB) 为单位Fig.6.(a) Time evolution of the mean probability in〉,(b) that in〉.The initial state is〉,and the time is in the unit of t0=1/(µ0ΔB).

5 结论与讨论

本文通过数值和解析两种方式研究了量子中继过程中两个半导体量子点的纠缠态的退相干规律.数值结表明,外磁场为零时,不管体系的初态为4 个Bell 基中的哪一个态,由于核自旋的影响,体系最终仍处于初态的平均几率即初态保真度约为0.34,而跃迁到另外3 个Bell 基态的平均几率约为0.22.当有外加磁场存在时,间的跃迁被外磁场压制,并且当外磁场增大到一定值时,间的跃迁被完全禁止.结果表明,由于外加磁场抑制了间的跃迁,从而可以提高系统初态的保真度.值得一提的是,Merkulov[25]发现在单个量子点中,随着外加磁场的逐渐增大,自旋取向与外磁场方向一致,因此核自旋仅会导致相位噪声而不会导致自旋翻转错误,我们的理论研究也再次印证了这一结果.并且与单个自旋不同的是,在双量子点纠缠态中,研究了外加磁场及核自旋对4 个Bell 基演化的影响.在较大外磁场时,间不能相互跃迁,所以我们将两个自旋构成的四维量子系统约化为两个独立的二维系统,分别采用解析方法研究其量子态随时间的演化规律.解析计算结果表明,核自旋涨落是影响系统退相干的主要因素,退相干时间及最终保真度不受体系初态的影响,即4 组Bell 基的退相干时间均为t0,最终保真度均为1/2.但是我们也发现,在t0时间以内(t ＜t0),Bell 基表现出很大的差异.如果系统初态为,在含时演化过程中,对z方向磁场不敏感,因而系统仍处于的平均几率只是随时间呈指数衰减,没有周期性振荡.当系统初态为,在含时演化过程中,系统仍处于的平均几率在指数衰减的同时还伴随着频率为 4µ0B0的周期性振荡.z方向微小的磁场变化可引起很大的几率波动,因而在量子中继过程中,很难对其进行量子操控.从这方面而言,在量子中继中选更易于操控.

既然研究结果表明,系统的退相干时间主要受核自旋涨落的影响,即t0=1/(µ0ΔB),所以要延长退相干时间必须减小核自旋等效磁场的涨落.这要求将量子点中的电子囚禁在更小的范围内.当电子在更小的范围内运动时,电子自旋与更少数目的核自旋相互作用,因此电子自旋和核自旋相互作用常数aj将更小,从而延长t0.有两种方式可以实现以上目的,第一是降低量子点温度,低温条件可以抑制电子热运动;第二是选择电子波函数更紧致的硅半导体量子点来替代GaAs 量子点.期望本文的研究结果可以帮助更加深入地了解纠缠态的退相干机制,进而利用半导体量子点的特性延长纠缠态的退相干时间.进一步期望该结果能为实际量子中继过程中,纠缠态选择问题提供理论支持和参考,从而提高实验中的量子中继效率.