580DP与700DP热轧双相钢的力学性能与成形性能

陈维晋，殷 胜，裴新华

(宝钢股份中央研究院梅钢技术中心，南京 210039)

0 引 言

随着汽车行业对节能、环保、安全的要求越来越高，先进高强钢在汽车结构件上的应用越来越多。双相钢因具有屈强比低、加工硬化指数高、烘烤硬化效果好，以及不存在屈服延伸和室温时效等优点而成为先进高强钢中应用最广的一类钢[1-2]。随着控轧控冷技术的发展，热轧板的尺寸精度、表面质量、性能稳定性得到显著提高，热轧钢也越来越多地替代冷轧钢而应用在汽车结构件上[3]。目前，汽车领域中应用较广泛的热轧钢为微合金高强钢，强度级别已经达到屈服强度700 MPa以上，但是由于微合金高强钢的屈强比高、加工难度大，因此主要应用于形状简单的零件，如座椅骨架等；而目前复杂形状零件的用钢需求量极大。

热轧双相钢由于具有冷轧双相钢类似的优点，在汽车底盘、车轮件上得到较多的应用。其中，580DP钢是应用最为广泛的一种热轧双相钢，主要应用在车轮的轻量化设计中[4-5]。但是，在进行翻边扩孔时，双相钢车轮零件容易出现开裂问题。综上，随着汽车轻量化的进一步发展，复杂结构零件的成形性能仍是制约材料高强减薄应用的重要因素[6]。成形极限曲线是目前用来评价材料成形性能的一种最广泛的方法，但是目前有关热轧双相钢成形极限的研究较少。为此，作者对580DP热轧双相钢与新型700DP热轧双相钢的力学性能、扩孔性能和成形极限曲线进行研究，并与相近强度级别的QStE550TM热轧微合金高强钢的进行对比；采用成形极限经验公式和MK模型对成形极限曲线进行预测，并与试验结果进行对比；基于厚度和断后伸长率对热轧双相钢成形极限曲线最低点主应变进行拟合，进而对成形极限经验公式进行修正。

1 试样制备与试验方法

试验材料为宝钢股份梅山基地采用控轧控冷技术生产的580DP热轧双相钢板(厚度3.00 mm)、700DP热轧双相钢板(厚度2.95 mm)、QStE550TM热轧微合金高强钢板(厚度3.00 mm)。为了降低钢中红铁皮缺陷出现的概率，采用低硅成分设计热轧双相钢。3种试验钢的化学成分如表1所示，显微组织如图1所示。由图1可知：580DP热轧双相钢组织中灰黑色马氏体占比为11.2%，白色铁素体占比为88.8%；700DP热轧双相钢组织中马氏体占比为24.6%，铁素体占比为75.4%；QStE550TM热轧微合金高强钢呈典型的铁素体和珠光体组织形貌，铁素体呈近似等轴状，珠光体弥散分布在铁素体晶界。通过对比可以看出，热轧双相钢的铁素体晶粒尺寸比微合金高强钢的大。这是因为热轧双相钢是通过相变得到马氏体来进行强化的，大尺寸的铁素体可以保证其优异的塑性变形能力；而微合金高强钢主要强化机制为细晶强化和析出强化，需要控制铁素体晶粒尺寸。

表1 不同试验钢的化学成分(质量分数)

图1 不同试验钢的显微组织

沿轧制方向截取标距为80 mm的拉伸试样，按照GB/T 228-2010，在INSTRON型万能材料试验机上进行室温拉伸试验，拉伸速度为2 mm·min-1，应变速率为0.001 s-1，试验过程中采用横向与纵向引伸计测应变，计算加工硬化指数和各向异性系数。在试验钢板上截取平面尺寸为150 mm×150 mm的试样，在试样中心冲制出φ10 mm的孔，按照GB/T 15825.8-2008，采用Interlaken-SP150型板材成形试验机进行扩孔试验，扩孔率λ的计算公式为

λ=(dh-d0)/d0

(1)

式中：d0，dh分别为扩孔前后孔的平均直径。

在试验钢板上截取长度为196 mm、中心宽度分别为20，40，60，80，90，100，120，140，160，180 mm的哑铃形试样，按照GB/T 15825.4-2008，采用Interlaken-SP150型板材成形试验机进行Nakazima胀形试验，半球形冲头的直径为100 mm。

2 试验结果与讨论

2.1 拉伸性能

由表2可知：与QStE550TM热轧微合金高强钢相比，580DP与700DP热轧双相钢均具有较低的屈服强度；700DP热轧双相钢的抗拉强度最高，QStE550TM热轧微合金高强钢的抗拉强度介于580DP与700DP热轧双相钢的之间；580DP与700DP热轧双相钢具有较低的屈强比，断后伸长率与加工硬化指数均高于QStE550TM热轧微合金高强钢的。可见，热轧双相钢具有更低的屈服强度和屈强比，以及更高的断后伸长率，因此加工性能更好。由于马氏体相变时无碳扩散，铁素体较纯净，强度较低，导致热轧双相钢的屈服强度较低，同时马氏体的存在导致抗拉强度高，因此热轧双相钢的屈强比较低。QStE550TM热轧微合金高强钢的强化机制为细晶强化和析出强化。细晶铁素体产生强化，且内部位错被晶界和析出相钉扎，因此该钢的屈强比较高。

表2 不同试验钢的拉伸性能

2.2 扩孔性能

由表3可知，QStE550TM热轧微合金高强钢的扩孔率比580DP与700DP热轧双相钢的高。热轧双相钢的软相铁素体与硬相马氏体之间的强度和塑性差异大。在外加载荷作用下，铁素体先发生大的塑性变形，而马氏体的变形量较小，因此两相界面处出现变形不协调现象。当因变形不协调而产生的应力集中达到使两相界面分离的程度时，两相界面处形成微孔或微裂纹，且裂纹扩展能力非常强[7-9]。这限制了热轧双相钢在有较高扩孔率需求零件上的应用。与700DP热轧双相钢相比，580DP热轧双相钢组织中马氏体含量较低，因此扩孔率略高。

表3 不同试验钢的扩孔率

2.3 成形极限曲线

由图2可知：580DP与700DP热轧双相钢的成形性能较好，成形极限曲线整体高于QStE550TM热轧微合金高强钢的；在右半部分的双拉变形区中热轧双相钢的成形极限曲线斜率大于QStE550TM热轧微合金高强钢的，说明热轧双相钢抵抗双拉变形的能力较好；580DP热轧双相钢的成形极限高于700DP热轧双相钢的，这主要是由于580DP热轧双相钢组织中马氏体含量较低，铁素体晶粒的等轴程度更高，使得断后伸长率和加工硬化指数更高导致的。3种试验钢成形极限曲线最低点的次应变不为0，而是略偏向双拉变形区，这与文献[10]中的结论一致。

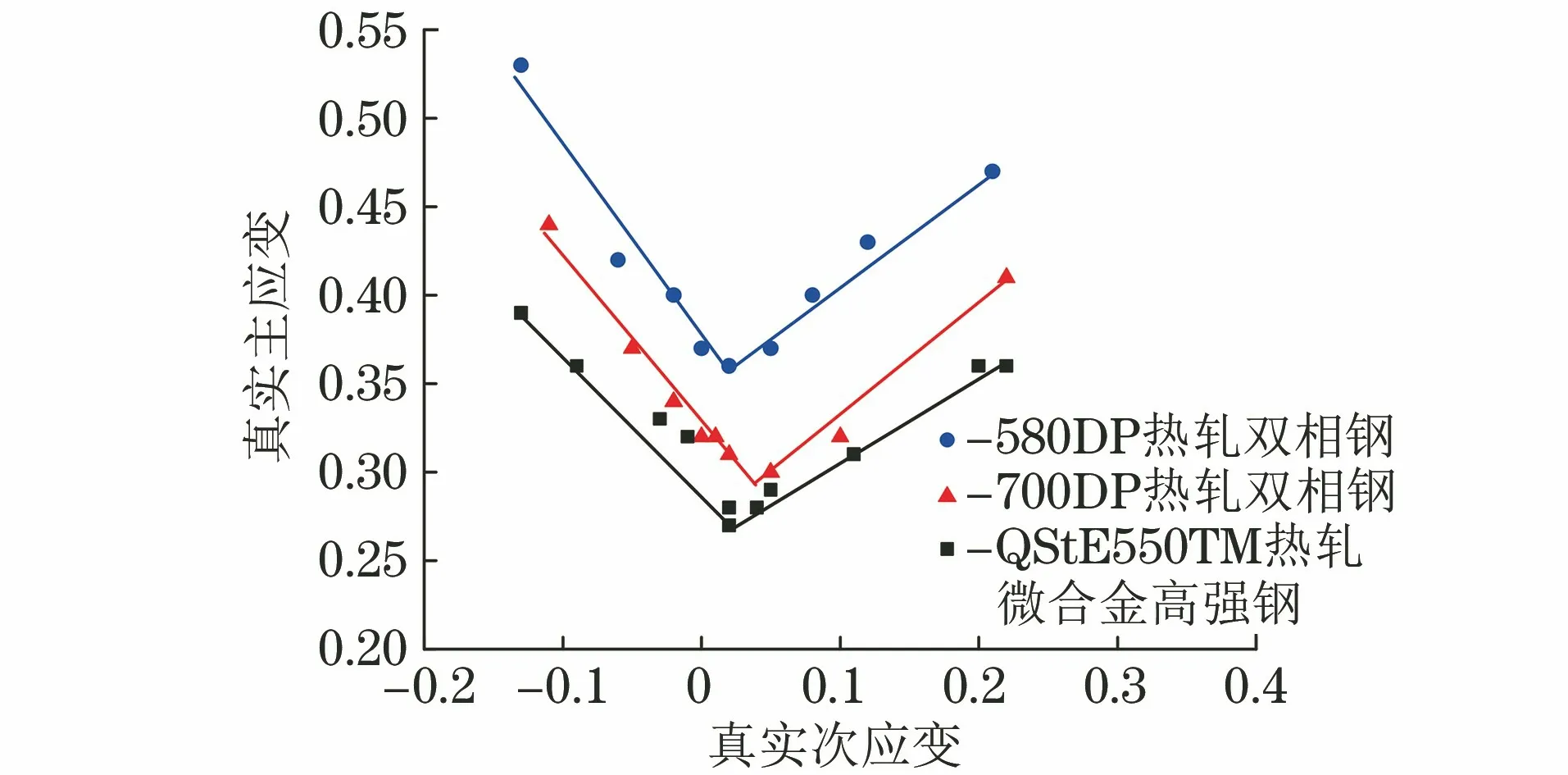
图2 试验测得不同试验钢的成形极限曲线

3 成形极限曲线的预测

3.1 常用成形极限模型的预测

在成形极限曲线的实际应用中，由于不同批次材料的性能与规格不同，采用试验方法获取成形极限曲线的成本高、效率低，因此材料成形极限曲线的预测是一项非常有意义的工作。目前，常采用经验公式对成形极限曲线进行预测，其中应用最为广泛的是Keeler公式[11]。

参考文献[12]，基于Keeler公式得到厚度大于2.5 mm钢板的成形极限计算公式：

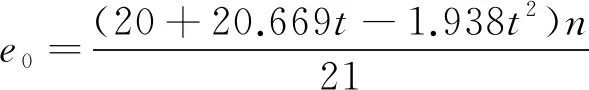
(2)

(3)

式中：t为钢板厚度；n为加工硬化指数；e1为工程主应变；e2为工程次应变；e0为成形极限曲线最低点的工程主应变。

对e1、e2进行对数转换即可得到真实主应变与真实次应变。为方便表述，将式(2)与式(3)定义为经验公式1。

参考文献[13-14]得到成形极限图曲线的另一种预测公式，具体为

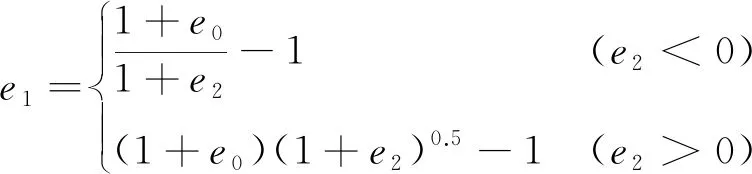
(4)

对e1,e2进行对数转换即可得到真实主应变与真实次应变。为方便表述，对应Keeler公式计算成形极限曲线最低点主应变的方法，将式(2)与式(4)定义为经验公式2。

参考文献[10]，通过拟合钢板的成形极限试验数据，并考虑了曲线向双拉变形区偏移的情况，得到与断后伸长率和钢板厚度有关的成形极限经验公式，具体为

ε0-major=0.695 1A(1-e-2t)+0.11

(5)

ε0-minor=0.178 6ε0-major-0.010 2

(6)

(7)

式中：ε0-major和ε0-minor分别为成形极限曲线最低点的真实主应变和次应变；ε1为真实主应变；ε2为真实次应变；A为断后伸长率。

为方便表述，将式(5)式(7)定义为经验公式3。

参考文献[15]，得到与断后伸长率、各向异性系数和钢板厚度有关的适用于先进高强钢的成形极限经验公式如下：

e0-major=0.008 4A+0.001 7A(t-1)

(8)

单向拉伸时的颈缩点应变计算公式为

ε1=(1+0.797r0.701)X

[0.062 6A0.567+(t-1)(0.12-0.002 4A)]X

[1+(0.797r0.701)2]-1/2

(9)

ε2=-[0.062 6A0.567+

(t-1)(0.12-0.002 4A)]0.797r0.701X

[1+(0.797r0.701)2]-1/2

(10)

等双拉时：

ε1=ε2=0.0021 5A+0.25+0.002 85At

(11)

0.75胀形区：

ε1=0.006 2A+0.18+0.002 7A(t-1)

(12)

ε2=0.75ε1=0.75[0.006 2A+0.18+

0.002 7A(t-1)]

(13)

式中：r为各向异性系数，由拉伸试验结果计算得到，见表2。

为方便表述，将式(8)式(13)定义为经验公式4。

MK凹槽模型是Marciniak和Kuczynski提出一种损伤失稳模型[16]，也是目前应用最为广泛的一个理论计算模型。以MK凹槽模型为基础，假设试样在变形过程中处于平面应力状态，参考文献[17]的计算方法得到3种试验钢的成形极限曲线。

将采用上述5种预测方法得到的极限成形曲线与试验结果进行对比，结果如图3所示。由图3(a)和图3(b)可知,上述5种方法都不能很好地预测580DP与700DP热轧双相钢的成形极限曲线。由经验公式1和经验公式2计算得到的成形极限曲线偏高，而由经验公式3、经验公式4、MK模型计算得到的成形极限曲线偏低；由经验公式1、经验公式2、经验公式4计算得到的右侧曲线斜率与试验结果接近，由经验公式2和MK模型计算得到的左侧曲线斜率与试验结果接近。由图3(c)可知：由经验公式1和经验公式2计算得到的QStE550TM热轧微合金高强钢成形极限曲线与试验结果比较接近；由经验公式3、经验公式4和MK模型计算得到的成形极限曲线整体偏低，其中由经验公式3计算得到的两侧曲线的斜率都偏高，由经验公式4计算得到的右侧曲线斜率与试验结果接近，而左侧曲线斜率过高，由MK模型计算得到的两侧曲线斜率都与试验结果接近。

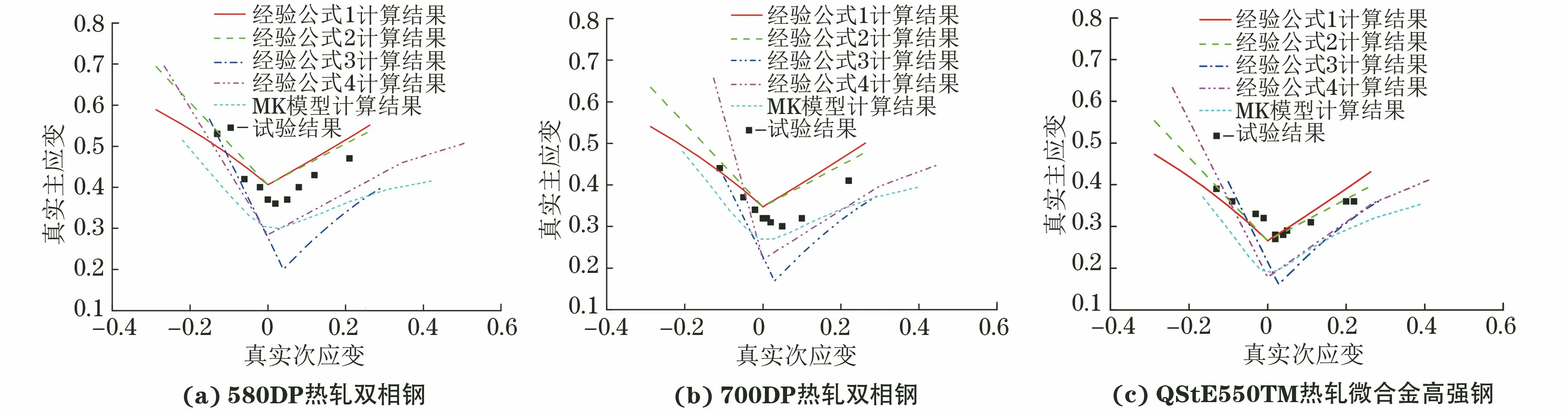
图3 不同方法计算得到试验钢的成形极限曲线与试验结果的对比

3.2 经验公式的修正

MK模型常用于薄板成形极限计算，且为了简化计算，通常假设试样在变形过程中处于平面应力状态；该模型对于较厚热轧钢板的计算效果较差，需要考虑厚度方向应力的影响[18]，计算复杂程度显著增加。Keeler公式是基于成形极限曲线的最低点只与加工硬化指数和钢板厚度有关而建立的，但是实际上材料的抗拉强度、断后伸长率、各向异性系数等也都会对成形极限产生影响[19]。并且热轧双相钢的成形极限与加工硬化指数的相关性较弱，而与断后伸长率的相关性较强[15]。根据成形极限曲线预测结果与试验结果的对比，基于式(8)对成形极限曲线最低点主应变进行拟合，并结合经验公式2的两侧曲线预测方法，对经验公式进行修正，从而对热轧双相钢成形极限曲线进行更准确的预测。基于表4中试验测得的不同厚度热轧双相钢的断后伸长率、成形极限曲线最低点的主应变，得到580DP和700DP热轧双相钢的成形极限曲线最低点真实主应变的拟合公式为

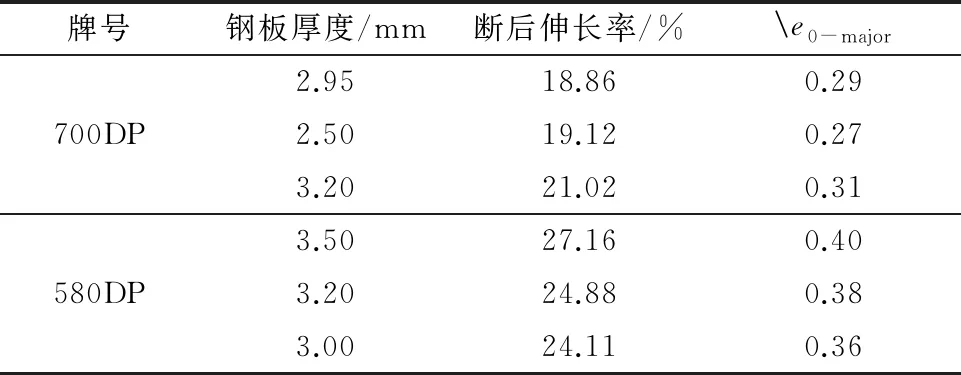
表4 试验测得不同厚度热轧双相钢的断后伸长率、成形极限曲线最低点真实主应变

ε0-major=0.013 02A+0.000 9A(t-1)

(14)

由式(14)计算得到不同厚度热轧双相钢的成形极限曲线最低点主应变,其与试验结果相吻合，相对误差小于4.0%。

由图4可知，经验公式经修正后计算得到的热轧双相钢的成形极限曲线与试验结果较吻合，其中580DP热轧双相钢成形极限曲线的计算结果与试验结果的相对误差小于5.6%，而700DP热轧双相钢在平面应变区域的相对误差小于9.4%，而在其他区域的相对误差小于6.5%。

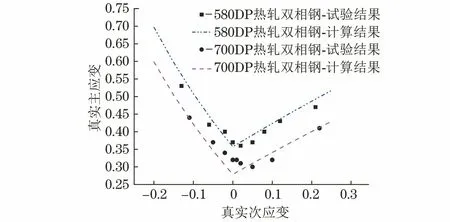
图4 由修正的经验公式计算得到热轧双相钢成形极限曲线与试验结果的对比

4 结 论

(1) 与QStE550TM热轧微合金高强钢相比，580DP与700DP热轧双相钢的断后伸长率和加工硬化指数较高，屈强比较低，加工性能较好；580DP与700DP热轧双相钢的扩孔率低于QStE550TM热轧微合金高强钢的，双相钢的扩孔性能较差；580DP热轧双相钢的成形性能优于700DP热轧双相钢的，且均优于QStE550TM热轧微合金高强钢的。

(2) 常用的成形极限经验公式与MK模型均不能很好地预测580DP与700DP热轧双相钢的成形极限曲线；基于不同厚度热轧双相钢的断后伸长率，拟合得到的成形极限曲线最低点主应变与试验值的相对误差小于4.0%，采用修正的成形极限经验公式计算得到的热轧双相钢的成形极限曲线与试验结果较吻合，其中580DP热轧双相钢的相对误差小于5.6%，而700DP热轧双相钢在平面应变区域的相对误差小于9.4%，在其他区域的相对误差小于6.5%。