基于运动学分析的行星滚柱丝杠副应力循环规律

2021-12-14姚琴刘永寿马尚君张猛创

华南理工大学学报（自然科学版） 2021年9期

姚琴刘永寿马尚君张猛创

(1.苏州科技大学机械工程学院，江苏苏州 215009；2.西北工业大学力学与土木建筑学院，陕西西安 710129； 3.西北工业大学陕西省机电传动与控制工程实验室，陕西西安 710072；4.西北工业大学民航学院，陕西西安 710072； 5.西北工业大学长三角研究院，江苏太仓 215400)

行星滚柱丝杠副(Planetary Roller Screw Mechanism，PRSM)是一种可以将直线运动和旋转运动进行相互转换的精密螺旋传动装置。作为机电作动器的关键执行机构之一，PRSM具有承载能力强、寿命长、传动精度高和空间适应性好等优点，被广泛应用于航天[1]、航空[2]、精密机床[3]和医疗器械[4]等领域。

PRSM由丝杠、螺母、滚柱、内齿圈和行星架等组成，其中丝杠、螺母和滚柱为主要承载零件。多个滚柱同时在丝杠与螺母之间做空间行星运动，通过滚柱两侧分别与丝杠和螺母螺旋曲面的啮合，可以将丝杠的旋转运动转换为螺母的直线运动，从而实现PRSM运动和力的传递。PRSM的运动特性会进一步影响其摩擦力矩[5]、接触特性[6]、动力学特性[7]和疲劳寿命[8]等，对PRSM进行运动学分析是其他各类研究的基础。

在PRSM的运动学方面，国内外学者展开了相应研究，并取得了一定成果。靳谦忠等[9]分析了PRSM的传动原理，得到了零件之间的运动关系；Hojjat等[10]采用图解法分析了PRSM在传动过程中的滑动趋势；Velinsky等[11]研究了考虑弹性变形时PRSM在接触区域内的滑动状态；Jones等[12]建立了包含滚柱轴向窜动的PRSM运动学模型，推导了滚柱的轴向偏移角度和滑动速度；党金良等[13]研究了反向式PRSM的运动原理及参数选择；马尚君等[14]研究了反向式PRSM中由滚柱节圆偏移造成的零件相对滑移；Liu等[15]计算了PRSM内零件的传动比；Ma等[16]建立了考虑螺纹旋向的PRSM运动学模型；Fu等[17]分析了零件偏心误差和位置误差对PRSM运动状态的影响；Sandu等[18]创建了PRSM单自由度的无量纲滑移比运动学模型，用于计算接触区域内任一点的滑动速度矢量。然而，基于PRSM内部零件不同运动特性的应力循环规律研究却鲜见报道。

文中基于丝杠、螺母和滚柱的空间螺旋曲面特征，通过参数方程形式建立PRSM的运动学分析模型，得到零件螺旋曲面上任意一点的运动方程与速度矢量；然后，根据啮合原理获得丝杠与滚柱、螺母与滚柱接触点的位置，再由接触点的速度矢量推导出PRSM的结构参数关系，从而获得丝杠、螺母和滚柱的空间运动轨迹及零件螺纹牙上的应力循环规律；最后，通过零件的应力循环次数预测PRSM的工作寿命。

1 螺旋曲面参数表示

1.1 空间坐标的建立

{x=rcosα

y=rsinα

z=f(r，α)， (r，α)∈Ω

(1)

为了区分零件上参与接触的螺旋曲面，同时兼顾参数方程表达的简洁性，令上、下截面轮廓关于x轴对称，如图1(b)所示。由于螺纹牙截面轮廓只与参数坐标r有关，若将其记为φ(r)，则Q点的轴向位置可以表示为

(2)

式中，ζ为布尔变量，ζ=1和ζ=-1分别表示螺纹牙的下接触面和上接触面。

将螺旋曲面参数方程统一表示成向量形式：

(3)

图1 螺旋曲面的空间坐标示意图

为了使法线统一指向螺纹牙内侧，将螺旋曲面上任一点处的单位法向量规定为

(4)

(5)

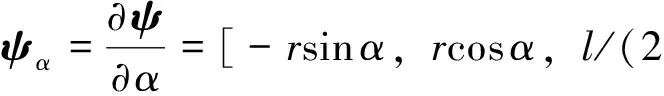
(6)

式中，ψr和ψα分别为ψ(r，α)对参数r和α的偏导数，φ′(r)为φ(r)对r的一阶导数。

1.2 丝杠螺旋曲面的参数表示

丝杠为具有梯形截面轮廓的多头外螺纹，如图2所示。丝杠中径、大径、小径、螺距、牙厚、牙型半角和螺纹头数分别为dS0、dS1、dS2、PS、hS、βS和nS，导程lS=nSPS。若螺纹牙上任意一点投影到xSOSyS平面内的极坐标为(rS，αS)，当dS2/2≤rS≤dS1/2时，丝杠螺纹牙型轮廓函数为

(7)

丝杠螺旋曲面参数方程可以表示为

图2 丝杠螺纹牙截面轮廓

{xS=rScosαS

yS=rSsinαS

(8)

将式(7)对rS求一阶导数，再代入式(4)-(6)中，则丝杠螺旋曲面上任意一点处的单位法向量为

(9)

1.3 螺母螺旋曲面的参数表示

螺母为多头内螺纹，螺纹牙截面轮廓为梯形，如图3所示。螺母中径、大径、小径、外径、螺距、牙厚、牙型半角和螺纹头数分别表示为dN0、dN1、dN2、dN3、PN、hN、βN和nN，导程lN=nNPN。若螺纹牙上任意一点投影到xNOyN平面内的极坐标为(rN，αN)，当dN2/2≤rN≤dN1/2时，螺母的螺纹牙型轮廓函数可以表示为

(10)

图3 螺母的螺纹牙截面轮廓

螺母的螺旋曲面参数方程及螺旋曲面上任意一点处的单位法向量分别为

(11)

(12)

1.4 滚柱螺旋曲面的参数表示

滚柱为单头外螺纹，其基本结构参数有：滚柱中径dR0，大径dR1，小径dR2，螺距PR，牙厚hR及牙型半角βR，导程lR=PR。为了减小摩擦、提高PRSM的传动效率，滚柱螺纹牙截面轮廓通常加工成如图4所示的圆弧形，圆弧半径为

(13)

图4 滚柱的螺纹牙截面轮廓

若螺纹牙上任意一点在xRORyR平面内投影的极坐标为(rR，αR)，当dR2/2≤dR≤dR1/2时，滚柱螺纹牙型轮廓函数为

(14)

同理，滚柱的螺旋曲面参数方程及螺旋曲面上任意一点处的单位法向量分别为

{xR=rRcosαR

yR=rRsinαR

(15)

(16)

2 运动学分析模型

为了更好地描述PRSM的运动特点，除丝杠、螺母和滚柱的零件坐标系外，还需设定固定坐标系O-xyz、固联在滚柱上的动参考系O1-x1y1z1以及t时刻的接触坐标系O-xcyczc。螺母坐标系ON-xNyNzN与O-xyz始终重合。当t=0时，丝杠坐标系OS-xSySzS与O-xyz重合，滚柱坐标系OR-xRyRzR中xR轴与x轴共线。PRSM的运动关系平面投影如图5所示，图中丝杠、螺母和滚柱分别用名义中径表示，即dN0=dS0+2dR0。假设PRSM匀速转动，并规定从z轴正端向负端看，零件逆时针转动为正，反之为负。

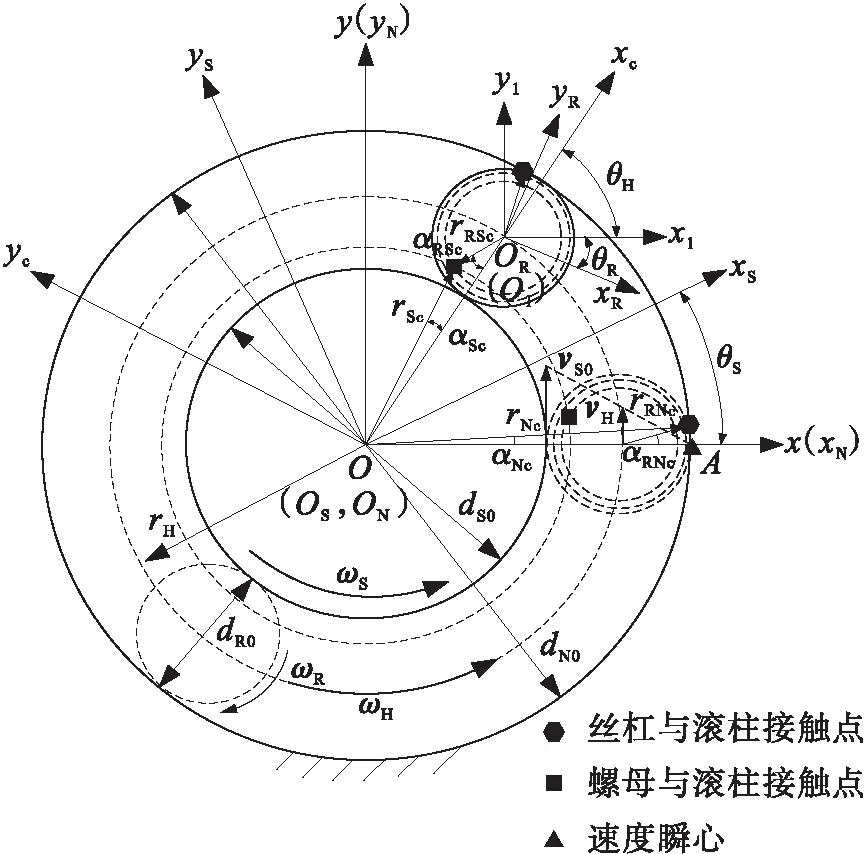
(a)PRSM的运动关系平面投影

(b)滚柱上点的速度合成

2.1 丝杠的运动学分析

当PRSM工作时，丝杠连接电机以角速度ωS绕自身轴线旋转且无轴向移动。经过时间t后，丝杠自转角度为θS=ωSt，丝杠螺纹牙上任意一点QS在OS-xSySzS中的位置由式(8)给出，进行坐标转换后，在固定坐标系O-xyz内，QS点的运动方程为

(17)

(18)

2.2 螺母的运动学分析

螺母为从动件，没有周向运动，只在轴向做与滚柱无相对位移的直线运动。由式(11)可得螺母螺纹牙上任意一点QN经过时间t后在O-xyz中的位置，即其运动方程为

(19)

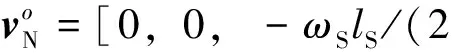
(20)

2.3 滚柱的运动学分析

多个滚柱通过行星架均匀分布在丝杠圆周方向并做行星运动，滚柱的公转角速度和自转角速度分别为ωH和ωR，公转半径为rH=(dS0+dR0)/2。滚柱螺纹牙上任意一点QR在O-xyz中的绝对运动可以分解为QR点在O1-x1y1z1中的相对运动和O1-x1y1z1在O-xyz中的牵连运动。其中，QR点的相对运动为滚柱绕自身轴线的定轴转动，牵连运动又可以分解为滚柱绕丝杠轴线的圆周运动和轴向的直线运动。当滚柱公转和自转角度分别为θH=ωHt和θR=ωRt时，QR点在OR-xRyRzR中的位置可由式(15)表示，经坐标转换到O1-x1y1z1中后，QR点的相对运动方程为

(21)

式(21)对时间t求导即得QR点在O1-x1y1z1中的相对速度矢量vRr：

vRr=[rRωRsin (αR-θR)，-rRωRcos (αR-θR)，0]

(22)

(23)

(24)

牵连点在O-xyz中做圆周运动的角速度为ωH，参考式(18)，可将圆周运动速度矢量vRH表示为

(25)

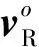
(26)

此外，O1点在固定坐标系O-xyz中的位置为

(27)

由式(21)和(27)可得QR点在O-xyz中的绝对运动方程为

(28)

3 运动特性与应力循环规律

3.1 接触点位置分析

3.1.1 丝杠与滚柱接触点的位置

rScsinαSc=rRScsinαRSc

(29)

rSccosαSc+rRSccosαRSc=dS0/2+dR0/2

(30)

根据连续相切接触条件[19]，丝杠在接触点的单位法向量nSc和滚柱在该点处的单位法向量-nRSc应该共线，即nSc=-nRSc。由丝杠和滚柱的单位法向量表达式(9)和(16)可整理出如下关系：

(31)

(32)

式中，ζSc=1和ζSc=-1分别表示接触点在丝杠的下接触面和上接触面，ζRSc表示滚柱螺纹牙上与丝杠接触的面，且ζRSc=-ζSc。联立式(29)-(32)可以得到未知数rSc、αSc、rRSc和αRSc。

3.1.2 螺母与滚柱接触点的位置

在螺母与滚柱接触侧，螺母的接触半径和接触偏角分别为rNc和αNc，在xNONyN平面内的极坐标为(rNc，αNc)；滚柱的接触半径和接触偏角分别为rRNc和αRNc，在xRORyR平面内的极坐标为(rRNc，αRNc)。螺母与滚柱在接触点存在如下关系：

rNcsinαNc=rRNcsinαRNc

(33)

rNccosαNc-rRNccosαRNc=(dN0-dR0)/2

(34)

另外，螺母和滚柱在该点的单位法向量满足关系nNc=-nRNc，由式(12)和(16)可得

(35)

(36)

式中，ζNc=ζRSc，ζRNc=-ζRSc，分别表示螺母和滚柱螺纹牙上参与接触的面。同理，联立式(33)-(36)可以得到未知数rNc、αNc、rRNc和αRNc。

3.2 接触点速度分析

3.2.1 丝杠与滚柱接触点处的速度分析

(37)

(38)

(39)

为了保证PRSM正确运动，滚柱与丝杠在接触点处速度的法向分量必须保持一致，即满足

(40)

其中，丝杠在接触点处速度的法向分量为

(41)

滚柱在与丝杠接触点处速度的法向分量为

(42)

将式(31)乘sinαSc与式(32)乘cosαSc相减可得

(43)

将式(43)代入式(42)，即有

(44)

联立式(40)、(41)和(44)可整理出ωR与ωH满足如下关系：

(45)

3.2.2 螺母与滚柱接触点处的速度分析

(46)

(47)

同理，滚柱与螺母在接触点处满足如下关系：

(48)

螺母在接触点处速度的法向分量为

(49)

滚柱在与螺母接触点处速度的法向分量为

(50)

将式(35)乘sinαNc与式(36)乘cosαNc相减可得

(51)

将式(51)代入式(50)即有

(52)

联立式(48)、(49)和式(52)可整理出如下关系：

(53)

3.3 结构参数关系

(54)

则ωR与ωH满足以下关系：

(55)

此外，由瞬心位置还可以得出丝杠中径的线速度vS0与滚柱圆心的线速度vH存在如下关系[9]：

(56)

因此，ωH可以表示为

(57)

若令kω=dN0/dR0，由以上推导可以整理出PRSM的结构参数与运动满足如下关系：

(58)

3.4 空间运动轨迹

计算结果表明，丝杠与滚柱具有一定接触偏角，接触半径均大于二者中径，并在接触点处存在相对速度。螺母与滚柱的接触点在二者轴心连线上，接触半径分别等于二者中径，且该点为速度瞬心。将接触点对应的极坐标分别代入丝杠、螺母和滚柱的运动方程，可以得到零件的空间运动轨迹，如图6(a)所示，图6(b)-6(d)为滚柱上与螺母接触点的运动轨迹平面投影。

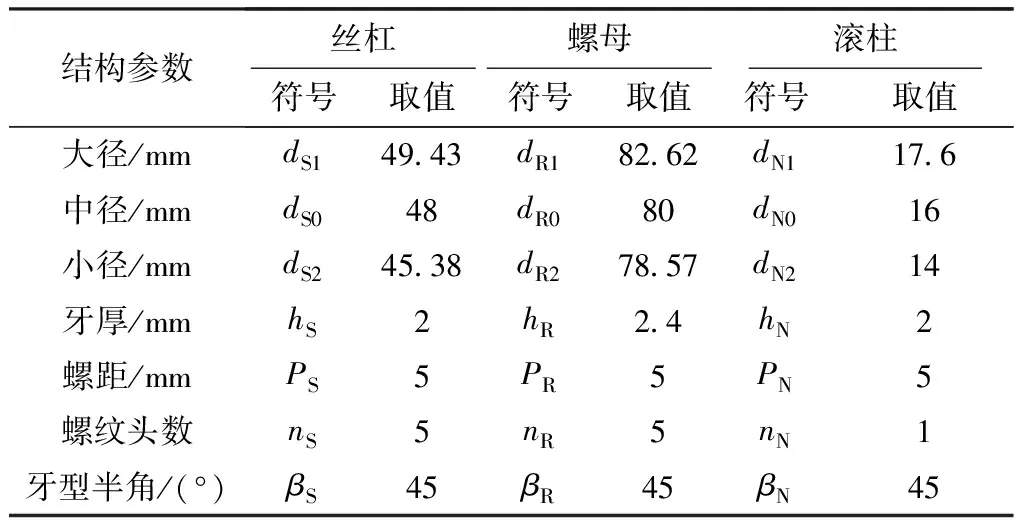
表1 PRSM结构参数

表2 接触点的位置参数及速度矢量

(a)零件空间运动轨迹

(b)滚柱运动轨迹的xOz平面投影

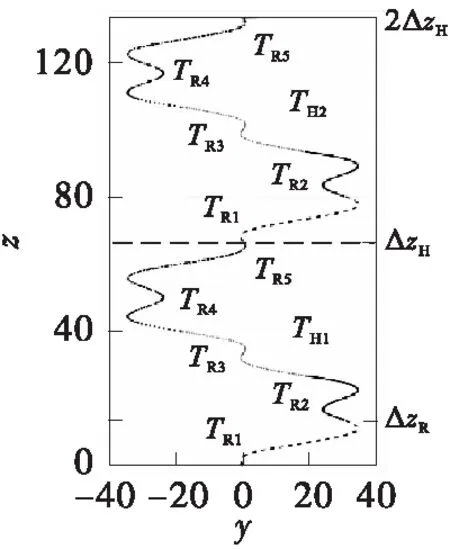
(c)滚柱运动轨迹的yOz平面投影

(d)滚柱运动轨迹的xOy平面投影

随着PRSM的运动，丝杠上接触点的运动轨迹为一平面圆，螺母上接触点的运动轨迹则为与轴线平行的直线，滚柱上与螺母接触点的运动轨迹为一条光滑的空间曲线。滚柱自转一周的轴向位移量ΔzR和公转一周的轴向位移量ΔzH可以由式(58)得到：

(59)

(60)

3.5 应力循环规律

(61)

当PRSM运动和承载处于静平衡状态时，滚柱螺纹牙上某个具体的接触点每间隔TRc时间便承载一次，即该点承受着稳定的脉动循环载荷FR及接触应力σR的作用，如图7所示。

图7 滚柱上载荷及接触应力的循环变化

当丝杠旋转一周时，滚柱上同一点发生接触的次数nRc为

(62)

对于螺母螺纹牙上某个确定的接触点，每个滚柱滚过就承载一次，该点也承受着稳定的脉动循环载荷FN及接触应力σN的作用，如图8所示。由于

图8 螺母上载荷与接触应力的循环变化

z个滚柱均匀分布，该点发生相邻两次接触的周期TNc为

(63)

当丝杠旋转一圈时，螺母上同一点发生接触的次数nNc为

(64)

丝杠上与某个滚柱的特定接触点在经过TSc时间后与下一个滚柱再次发生接触，即丝杠上同一点相邻发生两次承载的时间间隔TSc为

(65)

滚柱整个螺纹段经过丝杠上某一点的时间TS为

(66)

(67)

在实际工作中，滚柱和螺母通常在PRSM的有效行程lPRSM内做往复运动。丝杠上某个具体接触点的承载会随着运动时间发生周期性的不稳定变化，其变化方式与PRSM的安装方式、受力状态、运动方向、螺纹牙载荷分布等多种因素有关，即该点承受着周期性变幅循环载荷与接触应力的作用。图9为某种情况下丝杠中间螺纹牙上某点的载荷与接触应力变化示意图，图中TPRSM为滚柱和螺母在有效行程内完成单次运动的时间，

(68)