接触率作为流行指数函数的SEIR模型的全局稳定性

肖冰芯，薛亚奎

(中北大学 理学院， 太原 030051)

描述传染病传播的数学模型是数学在生物数学中最成功的应用之一[1]，但他们是通过使用统计力学中平均理论的方法得到的。换句话说，施动者是人或者动物，粒子近似，这可能构成了数学流行病中经典方法的主要限制：参与传染病传播的主体不是粒子，他们的行为包括心理方面，在形成人口动态中是最重要的。这是 Capasso和Serio在70年代首次强调，但只在最近几年清楚地认识到：人类行为包括不端行为应该被包括在传染病蔓延的某种方式的建模上，这引发了大量的科学研究。尽管各有各的方法，但所有的这些工作都明确包括了关于传染病的信息对病原体行为的反馈，从而反映出对目标疾病的传播的反馈[2-7]。

我们关注的是与疾病有关的信息对健康受试者行为的影响而给出的反馈，它在文献[2]中首次在SIR流行病模型中引入，其中，感染力被建模为感染主体比例的递减函数。在文献[3]中，Capasso和Serio的开创性工作得到了扩展，考虑到导致接触率降低的行为实际上受到了传播信息的影响，由于延迟和过去对流行病的了解，这些信息不仅反映了目前的传播状况，也反映了过去的传播状况。例如在指数衰减记忆核的情况下，存在一个唯一的地方病平衡点(EEP)，且局部稳定。

传染病作为一种严重危害人类的疾病，接触率在疾病传播过程中发挥着重要作用，当有关的传染病信息被媒体报道后，人们之间的接触率会下降，从而使染病者的数量减少[8-10]。介绍了一种SEIR模型，并定义信息相关行为对疾病感染力(FoI)的影响，通过构造适当的Lyapunov函数来研究它的全局稳定性[8]。

1 模型的建立

根据仓室模型思想，建立如下的常微分方程模型：

(1)

将总人口N(t)分为4类：易感者S(t)，潜伏者E(t)，感染者I(t)和恢复者R(t)。参数b(b>0)表示人口输入率与自然死亡率，不考虑因病死亡;易感者以比例β(M)SI感染并成为潜伏者，潜伏者以比例v(v>0)成为感染者，潜伏者和感染者的治愈率分别为r1，r2(r1，r2>0)，对感染者的治疗只有一部分q是成功的，即剩下的感染者p(p=1-q)治疗失败，治疗失败的感染者重新成为潜伏者。接触率是某一信息指标M(t)的函数[4]：

在本文中有：

(2)

函数g(I)描述的是传染量在信息动力学中所起作用的函数。

根据模型(1)和方程(2)，得到了一个新的模型：

(3)

模型(3)的初始条件：S(0)>0，E(0)≥0，I(0)>0，M(0)≥0

(4)

对于函数β(M)和g(I)有以下假设：

(H1):β(0)>0;β(M)>0;M>0

(H2):β′(M)>0;M>0

(H3):g(0)=0;g(I)>0;I>0

(H4):g′(I)>0;I>0

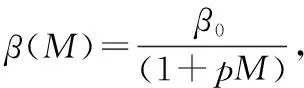
2 基本再生数和平衡点的存在性

模型(3)有唯一的无病平衡点P0=(1，0，0，0)。

根据基本再生数的定义[11]，模型(3)基本再生数R0的表达式为：

(5)

定理2.1当R0>1时，模型(3)存在唯一的地方病平衡点，记为P*=(S*，E*，I*，M*)。

证明令模型(3)的方程右端均等于0，求解得

且I*的解满足下式：

(6)

方程(6)的解可以看做是F1(I)和F2(I)的图像在第一象限的交点

使用假设(H1)和(H3)，及(5)中R0的表达式，可得

(7)

计算F1(I)的导数有

3 平衡点的稳定性

对于负反馈模型，使用以下的Lyapunov型函数[12-13]

(8)

使用假设(H1)和(H2)，可以验证函数U(M)在M=M*有一个全局最小值，并且满足U(M)≥U(M*)当且仅当M=M*时取“=”。

使用Volterra型Lyapunov函数：

V(x)=x-1-lnx

(9)

函数V(x)在x=1有一个全局最小值，且满足V(x)≥V(1)，当x=1时，两边相等。

β(M)满足假设(H1)和(H2)，对易感者的接触率β(M)进行了如下假设：

(H5): (Mβ(M))′>0,M>0。

引理3.1假设(H2)和(H5)成立，则

3.1 无病平衡点

定理3.1当R0<1时，模型(3)的无病平衡点P0在可行域Γ内是全局渐近稳定的。

证明令WS=V(S)，计算WS(S)的导数，得到

(10)

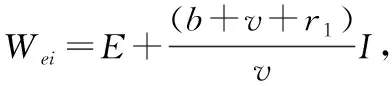
(11)

定义Lyapunov函数W:{(S，E，I，M)∈Γ∶S>0}→R

W(S，E，I，M)=cWS+cWei

(12)

其中，c∈R+，将上式相加得到W的导数：

由假设(H2)可知β(M)<β(0)

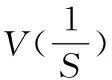
3.2 地方病平衡点

在特定条件g(I)=ωI下，证明地方病平衡点P*的全局稳定性。

定理3.2当R0>1时，模型(3)的地方病平衡点P*在可行域Γ内是全局渐近稳定的。

证明在EEP点，有

b=bS*+I*S*β(M*)

(13)

(14)

(15)

M*=ωI*

(16)

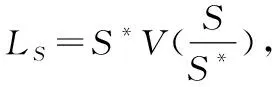
(17)

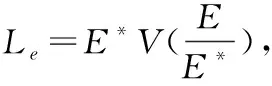
(18)

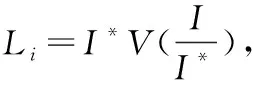
(19)

令Lm=U(M)，将式(16)代入，有：

(20)

构造Lyapunov函数

(21)

其中k∈R+，计算上式的导数，有

(22)

将式(17)～(19)代入式(22)，有：

(23)

式(23)中方括号之间的项是Volterra型函数，这些函数是正定的。

4 数值模拟和讨论

利用Matlab对研究的流行病模型进行数值模拟，验证模型(3)的无病平衡点及地方病平衡点的稳定性，考虑如下的情形：

取初始值S(0)=0.34，E(0)=0.31，I(0)=0.14，R(0)=0.21。

图1表示了无病平衡点的稳定性。当R0<1时，无病平衡点P0在可行域Γ内是全局渐近稳定的。通过合理提高潜伏期人群的治愈率和降低治疗失败的比例可以发现：R0减小有效地缩短了疾病趋于消亡的时间。

b=0.03，β(0)=0.05，v=0.04，r1=0.006，r2=0.003，p=0.01，q=0.99

图2表示了地方病平衡点的稳定性。当R0>1时，在特定条件g(I)=ωI下，地方病平衡点P*在可行域Γ内是全局渐近稳定的。通过合理提高潜伏期人群的治愈率和降低治疗失败的比例可以发现：R0减小有效地缩短了疾病趋于稳定的时间。

b=0.003，β(0)=0.05，v=0.04，r1=0.01，r2=0.008，p=0.01，q=0.99

5 结论

研究了一种具有信息变量M的SEIR模型(3)，一个对易感对象行为β(M)的负反馈，以及一个描述传染规模在信息动力学g(I)中所起作用的函数，给出了基本再生数R0，分析了无病平衡点P0及在特定条件下地方病平衡点P*的全局稳定性。

模型(3)地方病平衡点存在和唯一性的一个重要的流行病学结果是分析信息相关行为对感染力的抑制作用。信息的作用：① 增加易感者的平衡数量；② 减少感染和潜伏者的平衡数量；③ 使易感者增强防范意识，增强自身免疫力；④ 降低治疗失败的比例率，确保每位患者都痊愈再停止治疗措施。