偏置率和扭曲度对空气弹簧承载性能的影响研究
2021-12-14吴盛斌
谭 伟,吴盛斌,米 林
(重庆理工大学 汽车零部件先进制造技术教育部重点实验室, 重庆 400054)
相较于传统的钢板弹簧,空气弹簧由于其具有隔振效果好、刚度可变、舒适性高、更大程度的减少重载车辆对路面的冲击及更好的场景适应性和行驶通过性等优点,目前已被越来越多的应用于重型货车、危险货物运输车辆及挂车(半挂车)的悬架系统中,以提升上述车辆的驾乘舒适性及整体安全性[1-3]。
目前,国内外相关领域的学者和工程技术人员在空气弹簧相关力学性能方面进行了大量研究,由于空气弹簧中存在橡胶等超弹性材料与空气的耦合作用,因此主要研究方向集中在基础理论模型、数值仿真分析及可靠性分析等几个方面。李学兵等[4]建立了描述滚动凸叶空气弹簧和带状空气弹簧垂向刚度的解析式,并通过几何分析求解得到有效面积变化率方程。Bruni等[5]对空气悬架相关文献进行综述,将其运动模型分为热力学模型和等效力学模型,并描述了如何定义模型参数及不同参数对仿真精度有何影响。Majid等[6]通过有限元仿真和数字图像相关技术(DIC),对橡胶的超弹性性能进行研究,得到Yeoh模型可以对材料的应力-应变响应进行稳定的分析描述。刘国漪等[7]分析了初始气压、帘线层角度和帘线间距对空气弹簧垂向静特性的影响及在特定工作气压下振动频率对动刚度的影响。李阿午等[8]通过有限元仿真方法得到帘线材料及结构参数对空气弹簧垂向刚度的影响。叶珍霞等[9]利用有限元法分析气囊大变形的几何非线性、空腔内压缩气体的状态非线性及气囊与其他部件的接触非线性,得到了空气弹簧垂向刚度非线性特性的精确描述。
但上述研究主要针对空气弹簧的单一工况进行性能分析,未结合车辆行驶实际工况中存在的空气弹簧偏置率和扭曲度对其性能的影响。为了结合车辆行驶工况全面的分析空气弹簧承载性能的影响因素,本文应用有限元非线性理论建立空气弹簧的有限元仿真模型,仿真计算得到不同初始内压下空气弹簧的承载力-位移曲线,并与试验数据进行误差对比分析验证模型的正确性,在此基础上,分析了偏置率和扭曲度对空气弹簧承载性能的影响。
1 空气弹簧有限元模型建立
本文以膜式空气弹簧为研究对象,其结构如图1所示,基本性能参数如表1所示。

图1 空气弹簧结构示意图

表1 膜式空气弹簧基本性能参数
空气弹簧气囊的橡胶材料是各向异性的超弹性材料,其体积模量远大于弹性模量,在小变形阶段表现为材料的各向同性,大变形阶段由于橡胶分子链沿着拉伸方向重新排列,使其呈现出各向异性[10-12]。Mooney-Rivlin理论模型可较好地描述橡胶类不可压缩超弹性材料在大变形情况下的力学特性,其力学特性由应变能密度函数来描述:
(1)
式中:U表示单位参考体积的应变能;C10、C01和D1表示温度相关的材料参数,根据材料的拉压试验数据进行拟合来确定;I1和I2表示第一和第二偏应变不变量,定义为:

(2)
(3)
气囊的橡胶层主要起密封作用,内部的帘线加强层才是承载的主要部件,其通过硫化处理嵌入到橡胶层中组成气囊复合材料,以承受来自气囊内部压缩气体的载荷,且所受载荷随着气压的变化而不断改变[13-14]。帘线在工作过程中只发生小变形,可将其视为各向同性材料[15-17]。用ABAUQS软件中的Rebar单元对帘线层进行模拟,在定义Rebar单元时,帘线层方向角表示Rebar单元与中性面之间的夹角,帘线间距表示同一层帘线的布置密度,截面积表示帘线的粗细,其模型如图2所示。

图2 Rebar模型示意图
气囊承受的载荷来自其内部的压缩气体,而空气弹簧的承载性能主要由压缩气体的有效面积决定,当空气弹簧被拉伸或者压缩时,气囊内的气体压力和压缩气体的有效承载面积也随之改变,且压缩气体与气囊之间形成气固耦合[18-19]。ABAQUS/Standard中的流体腔(fluid cavity)行为决定着腔内压力、体积和温度之间的关系,可以准确地模拟空气腔内压缩气体作用于橡胶气囊的壁面压力,确保空气腔和气囊单元共用节点以实现空气压力和橡胶气囊结构之间的耦合作用。本文采用流体腔模块对空气弹簧内的压缩气体进行模拟。
对于整个空气弹簧模型,采用类型为S4R的壳单元模拟空气弹簧气囊橡胶层,定义单元厚度为气囊实际壁厚5 mm;橡胶材料参数C10=3.2、C01=0.8;帘线层结构参数设置如表2所示,且其材料杨氏模量为5 500 MPa、泊松比为0.28。上盖板和活塞底座都定义为刚体(rigid body),固定下底座,释放上盖板垂直方向上的自由度,并对上盖板施加垂直方向上的位移载荷以模拟拉伸和压缩工况。气囊和上盖与活塞底座之间的接触为硬接触,滑移量为有限滑移,摩擦系数为0.2。将上盖、气囊和活塞底座围成的封闭曲面定义为流体腔室,选择腔内中心线上一点为流体腔参考点,并施加工作气压。

表2 帘线加强层参数
基于有限元软件ABAQUS/CAE建立的膜式空气弹簧有限元模型如图3所示。

图3 空气弹簧有限元模型示意图
2 有限元模型误差分析
基于ABAQUS软件中建立的有限元仿真模型,首先,将空气弹簧调整到工作高度,即设计总成高度;然后依次向流体腔室中充入0.3、0.5和0.68 MPa的压缩气体,最后对上盖板施加垂直方向上±100 mm移载荷模拟空气弹簧的拉伸、压缩工况。记录分析过程中不同初始内压条件下的垂向位移与载荷等相关数据,其中初始气压为0.3 MPa时的压缩与拉伸应力云图如图4所示。

图4 空气弹簧压缩、拉伸应力云图
为了验证本文建立的空气弹簧有限元模型的准确性,参照《汽车悬架用空气弹簧——橡胶气囊》(GB/T13061—1991)对所研究的膜式空气弹簧进行等温变压垂向静力学特性试验。对空气弹簧静态垂向刚度进行试验的装置如图5所示。将空气弹簧调至工作高度后,向气囊中充入气体,直至内部气压稳定为0.3 MPa,关闭气阀,接着以20 mm/min的速度将上盖拉伸到-100 mm处,随即以相同速度将上盖压缩到100 mm处,记录压缩过程的位移-载荷曲线。完成后陆续充入0.5 MPa和0.68 MPa的压缩气体,重复上述试验步骤。

图5 空气弹簧试验测试装置布置
基于之前所做的工作,图6显示了在不同初始内压条件下,空气弹簧在试验和有限元仿真中所得到的位移-垂向载荷对比曲线,可见试验曲线和仿真曲线较为接近,最大误差不超过10%,满足工程设计误差要求,验证了有限元仿真方法的可行性。根据曲线的整体变化趋势,可知随着初始内压增大,空气弹簧的承载能力显著提升,此特性可使空气弹簧在工作高度不变的情况下,实现承载力无级调节,也可以通过改变初始内压来调节工作高度。

图6 不同初始内压条件下位移-垂向载荷曲线
3 偏置率和扭曲度对承载性能的影响
空气弹簧的理想工作状态是沿垂向作往复运动,但在安装或实际工作过程中会不可避免地产生其他方向的运动,使空气弹簧还受到来自非垂向的载荷,导致气囊的受力变形不均匀;除此之外,由于安装误差或螺栓松动等原因,空气弹簧工作时上盖或活塞底座会产生相对扭曲度,使气囊发生扭曲并产生沿轴向的扭矩,扭曲的产生会使空气弹簧橡胶气囊的使用寿命降低,这些因素都会对空气弹簧的承载性能产生影响。
3.1 偏置率的影响
偏置率α为上盖沿垂直于轴向的位移l与空气弹簧初始工作状态总高度h0的比值,定义如下式:
(3)
保持空气弹簧初始腔内气压为0.5 MPa,其他结构参数不变,依次使空气弹簧产生2%、4%、6%、8%和10%的偏置率,记录位移-垂向载荷曲线,如图7。由图7可得,随着偏置率的增大,空气弹簧的承载性能有所降低。这是由于偏置率使上盖和活塞底座所受垂向力的相对位置发生了偏移,空气弹簧在承受垂向载荷的同时还受到横向载荷,且力的偏移还会使空气弹簧承受弯矩,从而影响空气弹簧的承载性能。当偏置率小于6%时,承载力变化较小;偏置率大于8%时,承载力下降较为明显。因此,实际工作中,为保证空气弹簧的承载性能不受影响,应避免产生大于8%的偏置率。

图7 不同偏置率时位移-垂向载荷曲线
承载力的大小决定空气弹簧能承受的最大载荷,而其抵抗变形的能力由自身刚度决定。图8为不同偏置率条件下位移-垂向刚度曲线,可知垂向刚度在拉伸阶段的变化量较小,但在压缩阶段,垂向刚度随压缩量增加显著增大。这是因为空气弹簧有效承载面积变化率对其垂向刚度有很大影响,在拉伸阶段,有效面积变化速度慢,但压缩阶段,有效面积变化率显著增大。除此之外,偏置率越大,垂向刚度随压缩量增加而增大的速率越慢,相同压缩量时,垂向刚度随着偏置量的增大而降低。

图8 不同偏置率时位移-垂向刚度曲线
空气弹簧的设计分析通常只考虑其垂向性能,但实际工作中还会受到非垂向的载荷,产生偏置率,从而影响空气弹簧的承载性能。记录分析过程中的位和横向载荷数据,根据图9所示曲线可知,相同压缩位移下,偏置率越大,空气弹簧所受的横向载荷越大。且在同一偏置率条件下,空气弹簧所受横向载荷随着压缩量的增大而增大。这是由于相同条件下,压缩量正增大,会导致空气弹簧的横向刚度也随之增大[20]。
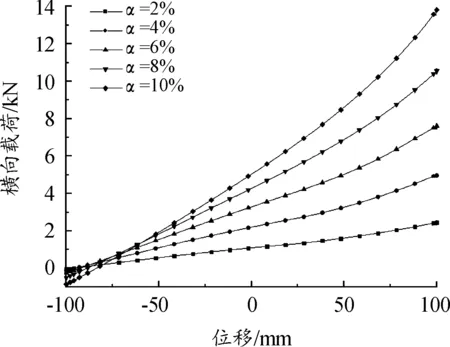
图9 不同偏置率时位移-横向载荷曲线
3.2 扭曲度的影响
定义扭曲度β为空气弹簧上盖和底座之间的相对转角,仿真中用上盖绕垂直方向的扭转角模拟空气弹簧的扭曲度,分别对上盖施加绕垂直方向且大小为5、10、15和20°的旋转角位移,分析空气弹簧承载性能随扭曲度改变如何变化,得到对应的位移-垂直载荷曲线如图10所示。由图10可知,20°范围内的扭曲度对空气弹簧对其承载性能基本无影响,这是因为考虑范围内的扭曲度对空气弹簧工作行程中有效承载面积变化情况的影响很小。

图10 不同扭曲度时位移-垂向载荷曲线
同样地,可以得到不同扭曲度条件下垂向刚度和位移的关系曲线,如图11所示,可知,20°范围内的扭曲度对空气弹簧垂向刚度几乎无影响。

图11 不同扭曲度时位移-垂向刚度曲线
虽然20°范围内的扭曲度对空气弹簧承载性能的影响很小,但扭曲度的存在使橡胶气囊发生扭曲,并在气囊上产生周向力,从而产生沿轴向的扭矩,其压缩量和扭矩的关系如图12所示。可知,扭曲度小于20°时,相同扭曲度条件下,拉伸量和压缩量改变,扭矩值无明显变化;同一拉伸或压缩量情况下,扭曲度增加,扭矩值显著增大。

图12 不同扭曲度时位移-垂向扭矩曲线
从图10、11可以得到,扭曲度对空气弹簧承载性能的直接影响很小,但图12说明,扭曲度的存在使橡胶气囊承受较大的扭矩,并产生扭曲,以削减橡胶气囊的使用寿命,从而影响空气弹簧的承载性能。所以在安装和实际工作过程中要避免空气弹簧产生扭曲度。
4 结论
本文以某型号膜式空气弹簧为研究对象,根据其结构参数,在ABAQUS软件中建立有限元仿真模型;根据建立的有限元模型得到空气弹簧不同初始内压条件下的位移-载荷曲线,并与试验数据进行对比,验证了有限元仿真方法的可行性;最后,基于建立的有限元仿真模型,研究了偏置率与扭曲度对空气弹簧承载性能的影响,得到如下结论:① 空气弹簧的承载性能随着偏置率的增大而降低,降低幅度逐渐增大;且受到的横向载荷随着偏置率的增大而增大。② 20°范围内的扭曲度对空气弹簧的承载性能无显著影响,但产生的扭矩随着扭曲度的增大而增大。
