整车半主动悬架系统的姿态补偿控制策略研究
2021-12-14吴麟麟许春妞汪若尘丁仁凯
吴麟麟,许春妞,汪若尘,丁仁凯
(江苏大学 汽车与交通工程学院, 江苏 镇江 212013)
半主动悬架因其减振器阻尼可调,性能优于被动悬架且成本低于主动悬架,发展越来越迅速。车辆行驶过程中的姿态变化可能影响到行车安全性及操稳性,因而对其控制刻不容缓。
国外的Mori等[1]提出了一种新的车轮姿态角主动控制方法,采用准稳态分析模型,研究了轮胎姿态控制对车辆横向运动的影响。Tchamna等[2]采用变刚度半主动悬架控制方法对车辆转向行驶姿态进行控制。Arana等[3]设计考虑悬架偏转积分以及微分作用的最优控制器,对车辆进行姿态控制。国内的谢健等[4]研究了包含直线电机主动悬架的整车姿态协调控制。陈双等[5]设计了转向工况下将LQG控制与模糊控制相结合的综合控制策略,优化车身侧倾姿态。
考虑现有针对车身姿态的控制大多采用单一的方法,或者只考虑单一的运行工况,导致车辆性能改善效果有限,且往往无法满足不同运行工况下的性能需求,本文设计如下姿态控制方法:利用天棚控制改善车辆平顺性,对于姿态控制,首先将根据车身纵向以及侧向加速度计算出俯仰侧倾补偿力,然后通过对整车系统进行模态分析分别计算出俯仰及侧倾能量并进行比较,从而进行补偿力权重系数计算及分配,最后将2部分力合成为减振器阻尼力,从而达到对车身姿态进行控制的效果。
1 整车半主动悬架系统模型
1.1 整车动力学模型
建立整车7自由度模型,如图1所示。
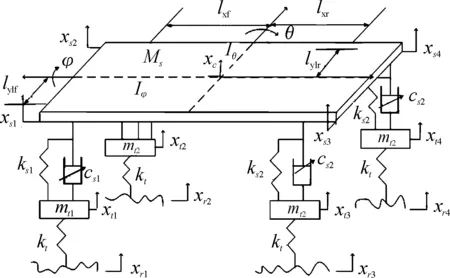
图1 整车7自由度模型示意图
整车微分方程如式(1)所示:
(1)
式中:
(2)
由于俯仰角及侧倾角较小,则可得:
(3)
xs(t)和q(t)的关系由下式建立:
(4)
应用牛顿第二运动定律,用质量、阻尼,以及刚度将整车悬架系统模型矩阵化表示如式(5)所示。
(5)
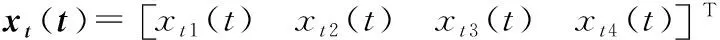
由上式可得:
(6)
整车参数如表1所示。

表1 整车参数
1.2 磁流变减振器模型建立
利用多项式模型[6]对磁流变减振器进行建模:
(7)
式中:ai为多项式拟合系数,且ai=bi+ciI,i为多项式拟合次数。则:
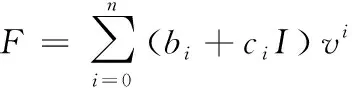
(8)
本次实验对象为输入电流在0~3 A的磁流变减振器,以0.25 A为间隔分别选取13组电流数据,在每一电流输入下分别进行外特性试验,试验台架如图2所示。

图2 磁流变减振器试验台架
外特性试验结果表明,磁流变减振器在13组不同电流输入下的特性曲线在减振器两端加速度分别为正和负时低速范围内减振器阻尼力存在较大差异,即存在滞回环[7],因此可根据加速度正负将外特性曲线分为上下两支,特性曲线如图3所示。
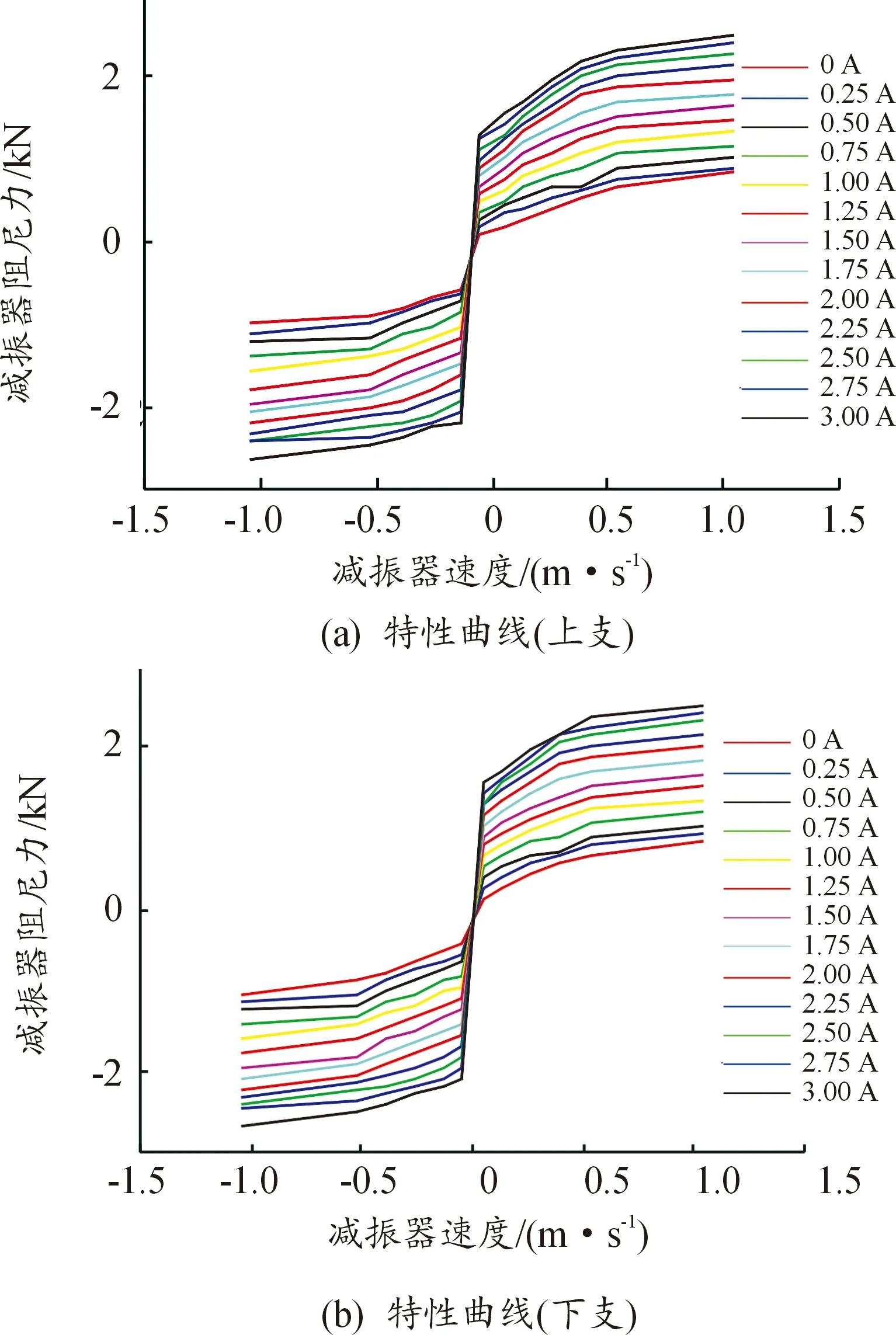
图3 磁流变减振器上下支特性曲线
利用Matlab/Curve Fitting工具箱分别对上下支特性曲线根据式(9)进行拟合:
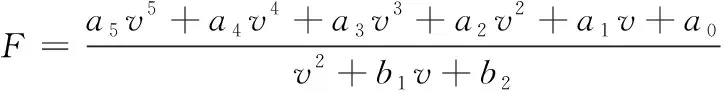
(9)
将多项式拟合结果与特性试验数据点进行对比。图4对比结果显示,多项式模型拟合的曲线与试验得出的数据点基本重合,有效验证了所建多项式模型的精确性。
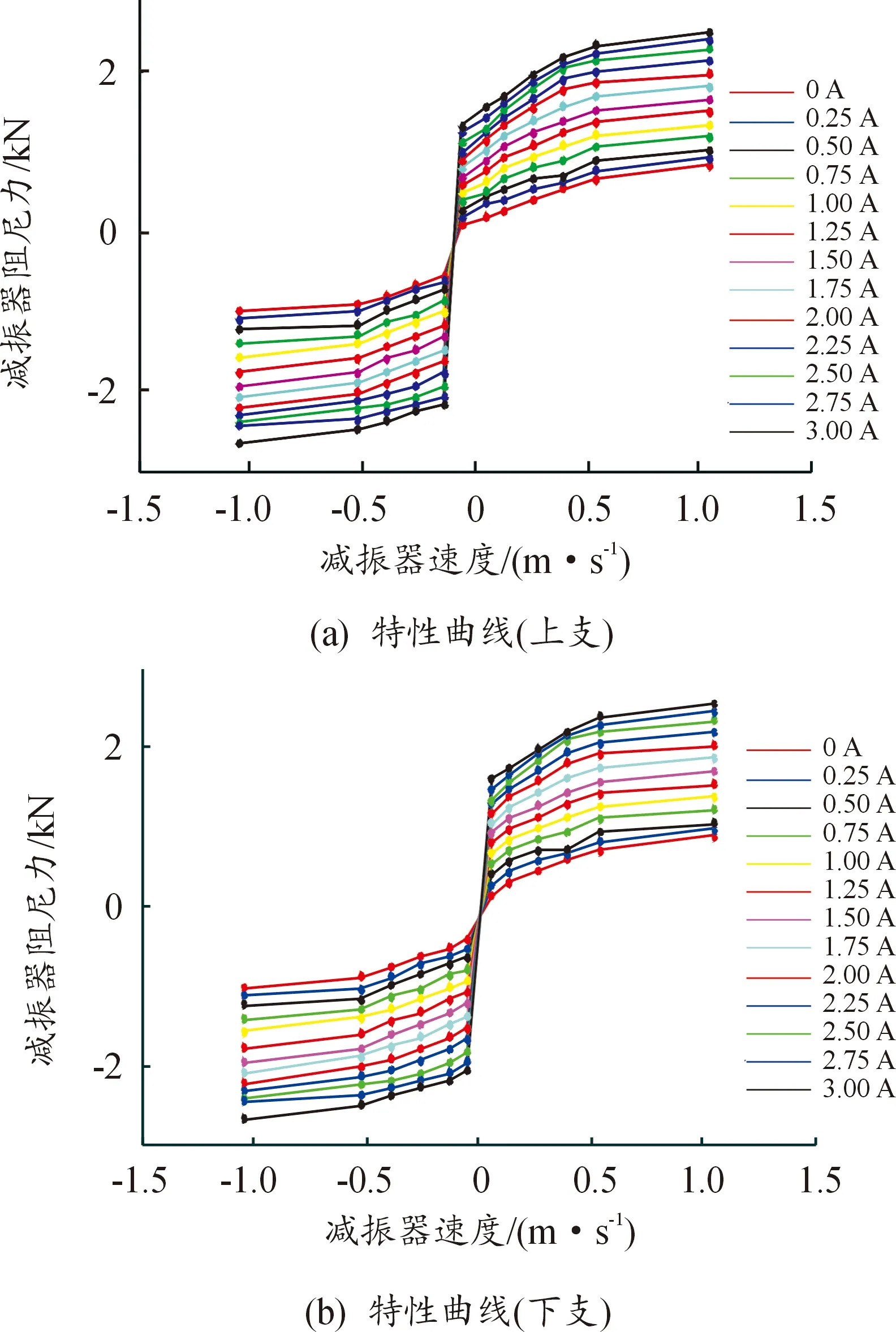
图4 磁流变减振器拟合数据与实验数据
2 整车半主动悬架系统控制算法设计
笔者设计的整车半主动控制算法主要分为2个部分,首先是针对车身垂向运动的天棚控制,其次是针对车身姿态变化采取的姿态补偿控制,目的是为了在保证车身垂向动力学性能的基础上改善车身姿态。
2.1 天棚控制算法设计
天棚控制的原理如图5所示。
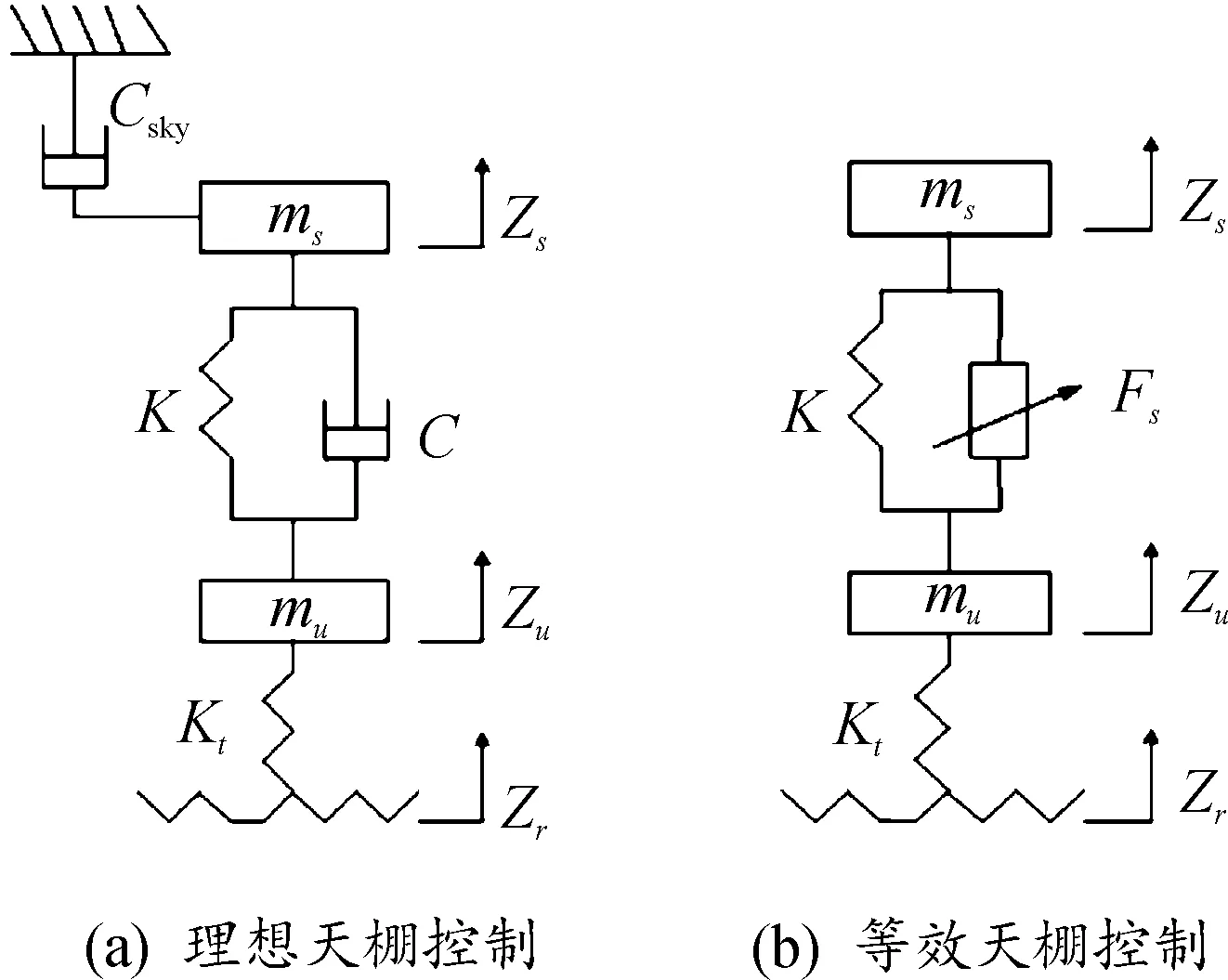
图5 天棚控制原理示意图
理想天棚控制由于实际情况的局限性可等效为在簧上簧下质量之间加入作动器[8],从而产生天棚控制力。
(10)
2.2 姿态控制算法设计
为了有效抑制车身姿态恶化,设计了整车姿态补偿控制策略。1/2悬架俯仰示意图如图6所示。
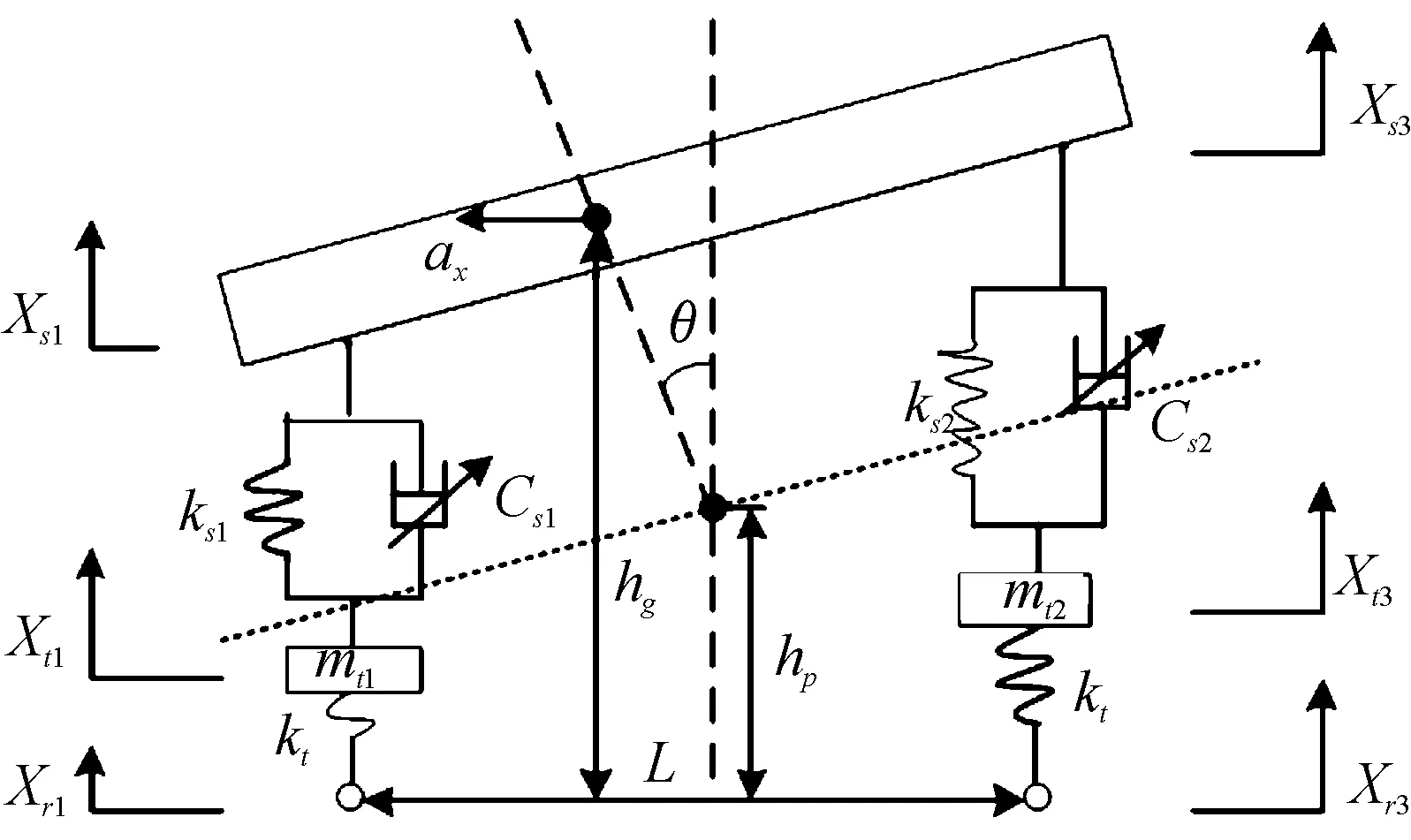
图6 1/2悬架俯仰示意图
以控制俯仰为例,车身产生俯仰运动时,可以通过调节减振器阻尼力来抑制其变化。当车辆纵向加速度为ax时,产生的俯仰力矩为:
Mp=ms·ax·hg
(11)
质心发生纵向位移产生力矩为:
Mx=ms·g·(hg-hp)·θ
(12)
前后载荷转移力矩为:
(13)
式中:Ftfl、Ftrl、Ftfr、Ftrr分别为左前、左后、右前、右后轮胎垂向力。
此时令前后悬架分别产生大小相等、方向相反的力ΔFP,则产生的抗俯仰力矩为Mf=2·ΔFP·L,且
Mp+Mx+Mtf+Mtr-Mf=0
(14)
则俯仰补偿力ΔFP可由上式求出,同理可得到侧倾补偿力ΔFR。其中:hg表示质心高度,hp表示俯仰中心高度、L为轴距。则左前、右前、左后、右后各悬架理想阻尼力分别由天棚控制力及姿态补偿力得出[9]:
(15)
式中:Fsfl、Fsfr、Fsrl、Fsrr为分别为左前、右前、左后、右后悬架天棚控制力。为避免理想阻尼力超出减振器有效范围,引入俯仰以及侧倾补偿力的权重系数,得到各悬架修正阻尼力:
(16)
式中:α、β分别为俯仰以及侧倾补偿力的权重系数。
基于以上公式,根据俯仰侧倾运动能量进行权重系数的计算,采用模态分析[10]方法计算车身运动能量,构造模态矩阵:
(17)

x(t)=Γp(t)
(18)
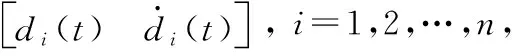
则第i个模式下存储的动能eki(t)和势能epi(t)为:
(19)
车辆俯仰运动的能量为:
e2(t)=ek2(t)+ep2(t)
(20)
侧倾运动的能量为:
e3(t)=ek3(t)+ep3(t)
(21)
则权重系数的计算规则如下:
1)e2>e3时,
α=1;β=e3/e2
(22)
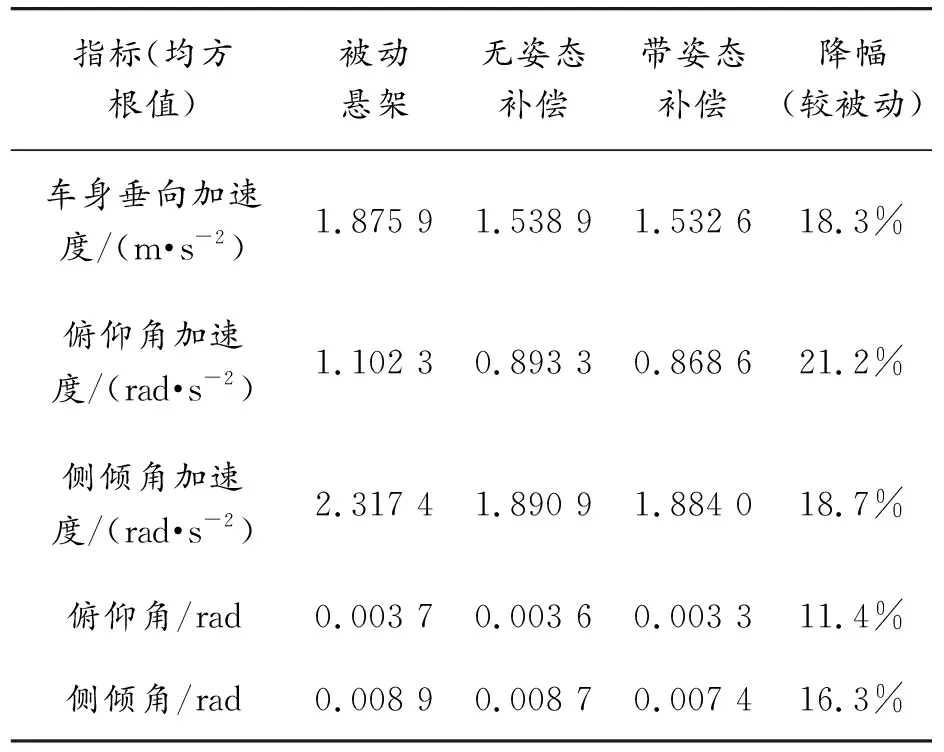
2)e2 β=1;α=e2/e3 (23) 3)e2=e3时, α=β=1 (24) 通过权重系数计算规则计算出α和β后,则根据式(16)求出各悬架修正阻尼力。利用式(25)判定各悬架修正阻尼力Fij′(i=F,R;j=L,R)是否在减振器阻尼力的有效范围之内。 (25) (26) 则可得此时输入磁流变减振器的电流I: (27) B、C级路面在我国公路等级中所占比例最大,且考虑到车辆动力学性能需求,往往路面等级越高则车速越高,反之越低。C级路面行驶车速往往在10~30 m/s。本文根据文献[11]中的方法在Matlab/Simulink中建立C级路面模型,选取行驶速度为20 m/s,在此路面激励下对采用本文设计的姿态补偿控制算法、未采用姿态补偿控制算法以及采用被动控制算法的车辆进行仿真对比分析,仿真结果如图7所示。 图7 C级路面仿真结果 根据表2可知:在C级路面激励下,笔者提出的姿态补偿算法可以对车身姿态变化有较好的抑制效果,因此认为此姿态补偿算法是有效的。 表2 C级路面仿真结果 利用式(28)建立凸块路面模型,令a=0.1 m,l=5 m,v0=20 m/s。对在此路面下车辆性能进行仿真对比分析,仿真结果如图8所示。 (28) 图8 凸块路面仿真结果示意图 由表3可知:采用姿态补偿算法的车辆在凸块路面行驶过程中可以有效抑制车身姿态恶化,且比未使用姿态补偿以及被动控制算法调整时间更短,更快恢复稳态。 表3 凸块路面仿真结果 受限于实验条件及成本,以硬件在环实验代替实车实验,所使用的平台为意昂神舟研发的HCU硬件在环测试系统。该系统由NI实时仿真机、控制器以及上位机组成。硬件在环实验结果对于本文设计的控制系统可行性验证具有重大指导意义。硬件在环[12]控制系统各部分组成如图9所示, 图9 硬件在环系统组成示意图 上位机系统通过Matlab/Simulink建立整车及磁流变减振器模型,负责定义运行工况,输入输出信号,并实时监测仿真运行状态,通过以太网实现与NI实时仿真机的通讯;NI实时仿真机下载并运行整车模型以及磁流变减振器模型,接收ECU控制信号,并输出整车状态信号;整车半主动姿态补偿控制算法代码通过编译下载到ECU中,ECU接受NI实时仿真机传递的整车状态信号,运算后输出各减振器控制电流信号,完成闭环控制。 分别在C级路面、凸块路面下20 m/s匀速行驶工况对笔者设计的姿态补偿控制算法以及未采用姿态补偿算法的车辆进行硬件在环试验,将试验结果进行对比,如图10所示。 图10 硬件在环实验结果 由图10可知,硬件在环实验中采用姿态补偿算法的车身垂向加速度、俯仰角均比无姿态补偿的车辆有较大改善,且与仿真结果基本重合,误差在可接受范围之内。 1) C级路面下车身加速度相比于被动悬架减少了18.3%,车身俯仰角加速度降低了21.2%,车身俯仰角改善了11.4%;车身侧倾角加速度减少了18.7%,侧倾角也有较大幅度改善,为16.3%。 2) 凸块路面下车辆车身加速度相比于被动悬架改善了20.8%,最大俯仰角改善了20.5%,且先于被动悬架0.72 s恢复稳态。 3) 硬件在环实验结果与仿真结果基本一致,且都表明:本文提出的控制算法对提高汽车的平顺性以及抑制车辆行驶过程中所发生的俯仰及侧倾姿态恶化都有较好的控制效果。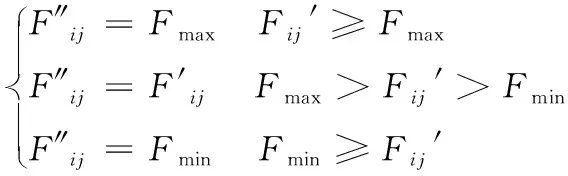
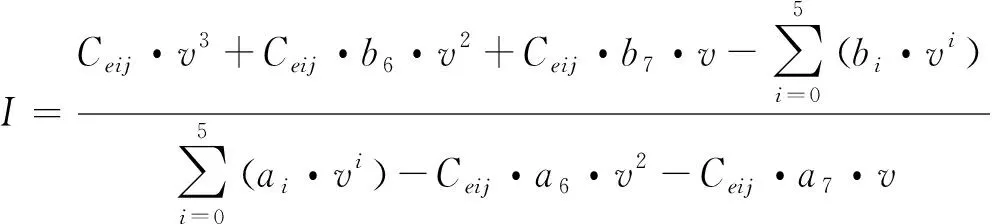
3 半主动悬架控制算法性能仿真验证
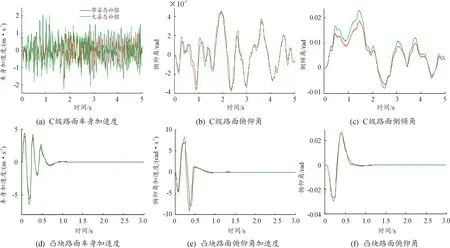
3.1 随机路面下整车姿态补偿控制效果分析

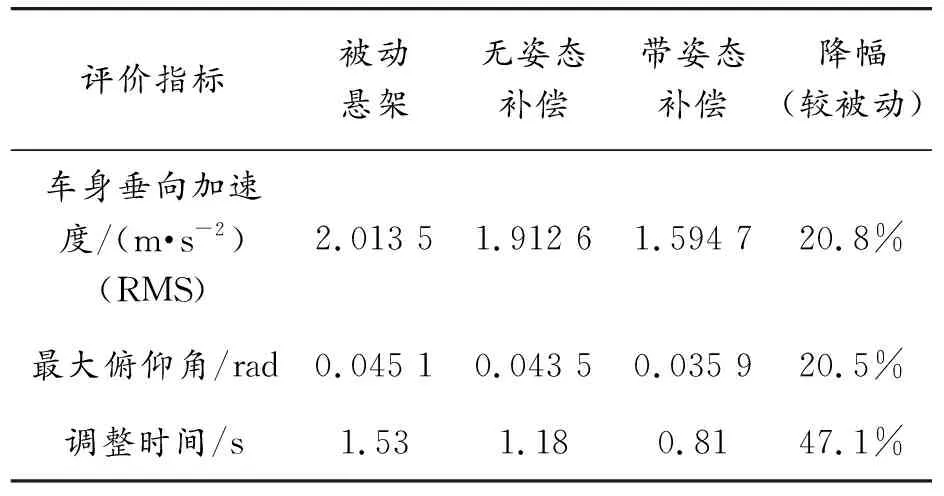
3.2 长坡形凸块路面匀速工况性能分析
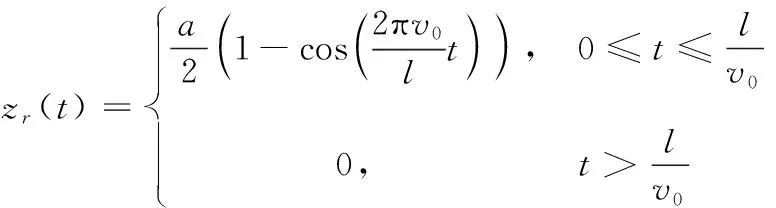

4 姿态补偿控制算法硬件在环测试
4.1 硬件在环方案设计

4.2 硬件在环试验结果分析
5 结论
