基于模型预测控制的车辆横纵向跟踪控制

邓国红,肖皓鑫,韩龙海，吴鹏飞,张 勇，覃 亮,2

(1.重庆理工大学 a.机械工程学院； b.车辆工程学院， 重庆 400054；2.重庆大江智防特种装备有限公司， 重庆 401320)

跟踪控制是实现车辆自动驾驶的关键一步，其目的是通过控制车辆的速度和前轮转向保证车辆按照期望的轨迹行驶。现阶段国内外对车辆的跟踪控制方法研究主要有：比例-积分-微分(PID)控制[1],其将真实输出值和参考值的偏差通过比例、积分、微分进行线性组合进行控制，广泛应用于工业界；反演控制[2]，将高阶的非线性系统细分为低阶子系统，选择合适的李亚普洛夫函数确保系统稳定，并求解出最优控制率；模糊控制[3]，根据工程经验，确定控制变量的模糊控制规则，常与PID算法结合形成Fuzzy-PID复合控制；预瞄跟随理论[4]，通过在道路前方设置一个预瞄点，控制预瞄点和车道中心线的横向位移为0来实现车辆对轨迹的跟踪；滑模控制[5]，在控制系统中设计一个滑模面，使状态量能在有限时间内到达滑模面的一种变结构控制方法；线性二次型调节器(LQR)[6]，适用于线性模型，通过反馈控制器使目标函数达到最小值；以及模型预测控制(MPC)[7]等多种方式。但由于车辆复杂性和运动的不确定性，目前的跟踪控制器进行轨迹跟踪控制时多数只控制车辆的横向运动，即控制车辆的前轮转角进行换道操作。

1978年，模型预测控制[8](model predictive control,MPC)这一概念被Richalet等学者提出，此后模型预测控制被大量应用在了车辆控制、智能产业中[9]。Sun等[10]提出了一种基于模仿学习与优化相结合的自动驾驶规划、控制模型，该模型包括两层结构，上层通过BP神经网络对MPC进行模仿来规划长期轨迹，下层通过MPC来进行跟踪，并通过2个高速驾驶实例验证模型的有效性。Chen等[11]基于自行车模型和8自由度模型建立了2个MPC控制器，并用2个控制器分别控制8自由度和14自由度车辆模型在特定工况下进行验证比较，论证了基于自行车模型的MPC控制器在运算速度上的优越性以及能更好满足实时性的要求，而8自由度的控制器能够更加充分考虑到转弯过程中车身侧倾与车轮载荷转移带来的影响。Liu等[12]研究了高速情况下自动驾驶车辆换道过程，在保证模型保真度和计算可行性的前提下，提出了变时间步长对动力学模型进行离散化的方法，以此保证足够长的预测时间。Luo等[13]提出了一种鲁棒MPC控制方法，该控制方法包含基于事件触发的(Event-Trigger)ETMPC控制器和状态反馈控制器，使系统在特定条件下在MPC控制和状态反馈控制间来回切换。该方法旨在减少MPC的计算量，并提升系统鲁棒性，在计算量和控制性能之间取得平衡。梁忠超等[14]提出了一种动态卡尔曼滤波和MPC相结合的控制策略，通过不断更新卡尔曼状态观测器中的增益矩阵补偿车辆非线性和测量噪声带来的影响，使控制器能适应变化的车辆系统。石贞洪等[15]采用以模糊控制来优化MPC控制器中目标函数权重系数的方法，使目标函数权重系数能根据跟踪误差以及路径曲率的变化进行动态调整，以此提升行驶安全性与系统稳定性。孙银健[16-17]考虑到算法的实时性问题，提出了非线性系统与线性系统之间的转化方法，以及如何用标准二次规划方法求解MPC模型。

在此前对于换道跟踪控制器的研究中，未考虑车辆在横向控制时的纵向运动控制，大多数是对横向的行驶方向和纵向的速度设计独立的控制器，且控制目标多为车辆的前轮转角而没有引入纵向速度控制量，跟踪过程中的纵向速度为定值，而车辆在换道过程中的行驶状态是由行驶方向和行驶速度共同决定的，没有考虑纵向速度的变化会大大降低控制精度和安全性。因此，本文以智能车为研究对象，以模型预测控制算法为基础设计了横纵向联合跟踪控制器，以前轮转角和纵向加速度作为控制量。首先建立车辆横纵向联合控制器的非线性预测模型，其次将非线性预测模型进行线性化处理，然后进行二次规划求解，最优求解车辆所需的前轮转角和加速度，最后进行仿真验证，验证本文设计的横纵向联合跟踪控制器的有效性和鲁棒性。

1 预测模型

使用何种预测模型是模型预测控制的关键内容，被控单元的效果由预测模型的精度决定，所建立的预测模型精度越高，预测的输出和被控单元的输出就会越贴近，但精度越高的模型伴随着更大的计算量，从而降低控制系统的响应速度。综合稳定性与实时性的考量，本文将会阐述如何选择适当的车辆模型作为横纵向跟踪控制器的预测模型。

根据文献[11]的表述，采用二轮3自由度模型(有横摆、纵向和横向3个自由度)作为预测模型(如图1所示)对车辆的轨迹进行跟踪时误差较小，能够输出理想的曲线。

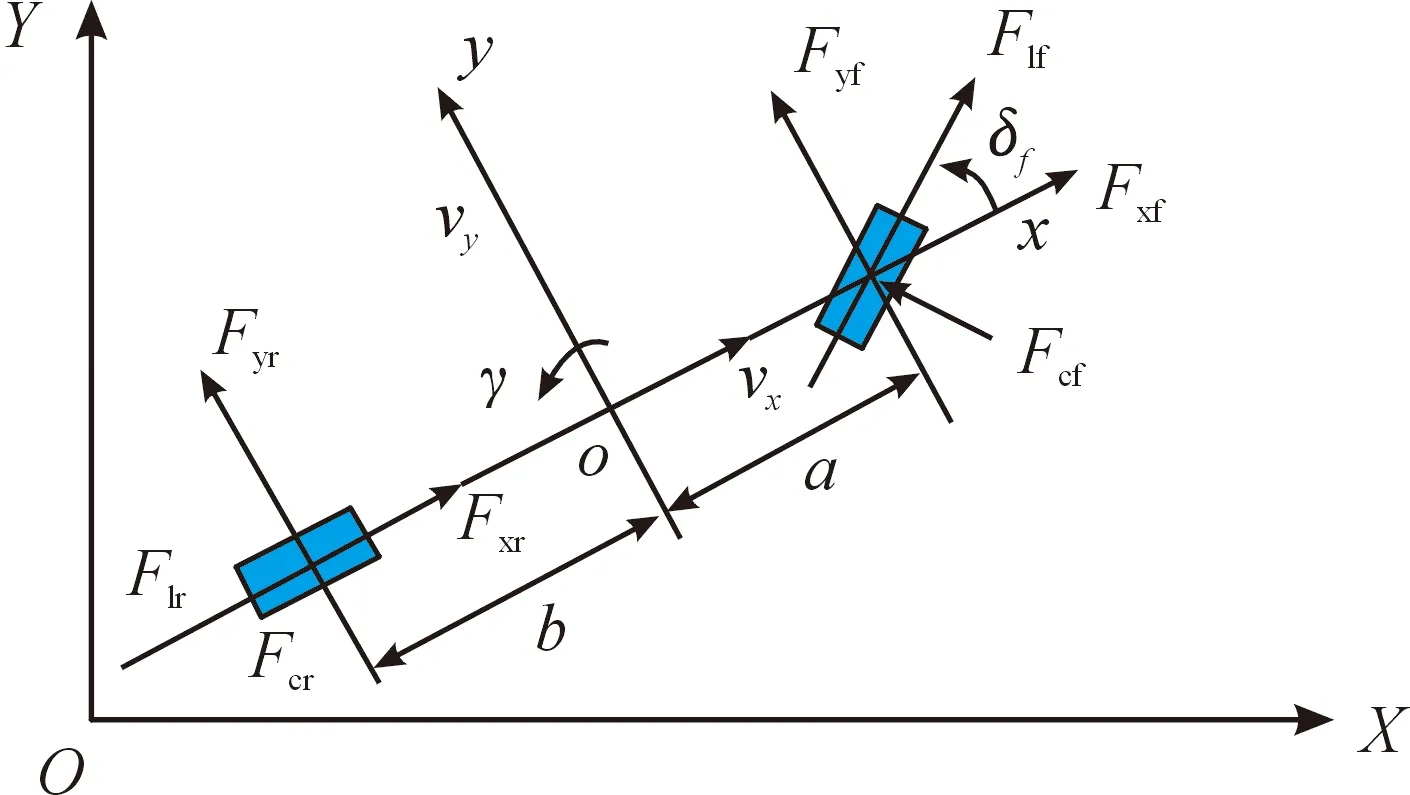
图1 3自由度车辆模型

根据图1所示，XOY是大地坐标系，将车辆质心作为原点，构建坐标系XOY、XOY坐标系中，X方向代表车辆的纵向运动方向，Y轴和1819轴由右手定则确立。车辆3自由度模型如式(1)所示。

(1)

式中：vx、vy分别为纵向速度、横向速度(m/s)；γ为车辆的横摆角速度((°)/s)；δf为前轮转角(°)；Flf、Fcf为地面施加于前轮的纵向力和横向力(N)；Flr、Fcr为地面施加于后轮的纵、横向力(N);Iz为z轴的转动惯量(kg·m2)；m为汽车质量(kg)；a为质心到前轴距离；b为质心到后轴距离(m)。

根据图1能够得到模型的前轮和后轮侧偏角αf、αr。

(2)

式中：vc、vl为轮胎的横向速度和纵向速度(m/s)。但由于车辆在行驶时，其纵向和横向的速度不容易直接获得，通常可以通过图1中汽车质心的纵向与横向速度vx、vy轮胎的转角以及其余参数求解得到。

(3)

(4)

在搭建预测模型前，需要对轮胎工作过程中的受力进行简化，因为轮胎具有显著的非线性特性，这样可以降低系统的复杂度。根据文献[18]的试验和使用魔术轮胎公式搭建的模型在仿真之后所呈现出的结果显示，在正常行驶的工况中，轮胎的纵向滑移率s以及侧偏角都小于或者等于 4～5,车辆侧向加速度ay≤0.4g，轮胎的侧偏角和侧向力之间，以及滑移率和纵向力之间的关系可以看作是线性关系。考虑到本文所涉及的车辆在换道过程中，轮胎力会一直处于线性区域内，所以采用式(5)求得轮胎纵、横向力。

(5)

由于模型中的车轮侧偏角在计算过程中有三角函数关系，而在实际行驶过程中，考虑到车辆的车轮转角和侧偏角数值都较小，因此可采用以下的假设条件：

sinθ≈θ,cosθ≈1,tanθ≈θ

(6)

θ值包括车轮转角以及侧偏角。

对前、后轮纵向力与横向力、车轮侧偏角进行化简后可得到式(7)～(9)：

(7)

(8)

(9)

在对轨迹进行跟踪时，控制器的参考轨迹往往建立于大地坐标系之上，如图2所示，所以还需要确立车辆位置与大地坐标系之间的关系，具体的关系方程由式(10)所示。

(10)

图2 大地坐标系下的车辆位置

联立式(1)～式(10)，得到横向模型，如式(11)所示。

(11)

此外还需要考虑车辆的纵向速度控制，以纵向位移x以及速度v作为纵向状态量，以加速度ax作为纵向控制量，最终确定点质量模型为横纵向跟踪控制器的纵向预测模型，如式(12)所示：

(12)

同样地，需要确定车辆位置系和大地坐标系之间的关系，其车速和大地坐标系下速度关系用下列方程表示：

(13)

综合车辆横向以及纵向运动预测模型得出，本文所设计的车辆横纵联合跟踪控制器的非线性预测模型如式(14)所示。

(14)

在式(14)中含有2个加速度变化量，由于车辆的纵向速度通过控制加速度得到，因此对其进行修正：

(15)

把上式改写成状态空间方程：

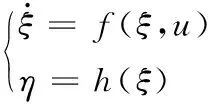
(16)

2 线性时变预测模型

由于式(14)所建立的模型是非线性的，对应使用的控制算法也是非线性的，然而在实际的控制过程中，模型要求控制过程的实时和稳定，非线性模型预测控制很难达到要求，此外还会形成较为复杂的非线性约束[19]。而将模型线性化之后，可以使控制器性能更符合要求。常用的线性化方法有近似线性化与精确线性化。本文选用近似线性化的方法，其原因在于：MPC控制器是一个闭环控制器，它的反馈矫正以及滚动优化的特征使其能够进行实时调节。每一个采样时刻都会根据控制对象的实际输出，调节预测模型的输出，不断优化更新，以减少因受外界因素扰动而产生控制输出和参考值之间误差过大的问题。除此之外，因为MPC要求较高的实时性，更精确的模型会要求更高的算力以及更容易产生一些难以排查的问题。

首先将前文中的非线性模型进行近似线性化，采用文献[20]中所使用的方法，线性时变方程如式(17)所示。

(17)

式中：

之后对式(17)进行离散化处理。

(18)

式中：Ak,t(k)=I+TAt(t)，Bk,t(k)=TBt(t)，Ck,t(k)=Ct(t)，Dk,t(k)=Dt(t),T为离散后的系统采样周期，ξd(k+1)=ξ(k+1)-ξ0(k+1)，ξd(k)=ξ(k)-ξ0(k)，ud(k)=u(k)-u0。

根据式(18)中的条件进一步处理可以得到：

(19)

式中：dk,0(k)=ξ0(k+1)-Ak,tξ0(k)-Bk,tu0ξ0(k+1)ξ0(k+1)指的是系统在整个采样周期中用连续的控制量u0所获得的新的采样时刻的状态量。

为了使控制器稳定运行，需要对控制量的变化量施加约束，因为上式中的控制量会在控制过程中产生跳变。此处把式(19)里的控制量u(k)改写成控制增量Δu(k)，将控制增量进行约束从而减少控制过程中的跳变，因此式(19)应改写为：

(20)

经过线性化和离散化后的状态空间方程为：

(21)

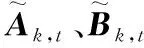
(22)

式中：Np表示预测时域，Nc表示控制时域，且Np≥Nc。

通过式(22)判断Np中系统未来每个采样时刻的状态量以及输出量。

此处把式(21)写作矩阵来表述Np中的系统状态量以及输出量。

(23)

式中各矩阵如下：

3 线性时变模型预测跟踪控制器

3.1 目标函数与约束问题

优化问题的重点在于目标函数，目标函数可以显示设计的系数追求的一些特定的目的。在目标函数的设计过程中，需要确保车辆可以平稳而且迅速地跟踪上期望路径以及期望速度。此外为确保求解器可以在约束条件限制下求得最优解，需要在目标函数中加入松弛因子ε。本文参考文献[20]，使用了二次型目标函数：

(24)

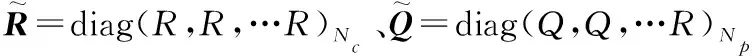
考虑到车辆行驶过程中的安全性，需要对输出量、控制量(ax,δf)、控制量增量(Δax,Δδf)作出如下约束：

(25)

把式(24)和式(25)整理过后得到系统的优化函数。

(26)

3.2 优化求解

式(26)设计的优化函数是二次型函数，二次型函数的求解，可以转化为二次规划问题，即：

(27)

在每个采样时间，都可以使用二次规划确定最优，算得控制器的最优控制序列：

(28)

在式(28)中，如果把第一项当成是目前时刻的控制增量，那么目前时刻的控制量就是上一个时刻控制量和目前控制增量的和，即：

u(k)=u(k-1|k)+Δu(k)

(29)

然后进行下一次求解，重复上述过程，获得最优控制序列。

4 仿真验证

在Matlab/Simulink和CarSim软件中搭建横纵向联合跟踪控制器以及车辆动力学模型，整车参数如表1所示。

表1 整车参数

目前国内外大多数研究智能车辆的换道路径跟踪性能时选择等速偏移的换道轨迹、正反梯形加速度的换道轨迹、圆弧的换道轨迹和多项式的换道轨迹。本文选取5次多项式换道轨迹作为车辆横向跟踪的参考轨迹，纵向运动跟踪参考速度选择基于sin的函数参数。

车辆横向运动参考轨迹表达式为：

y(x)=a5x5+a4x4+a3x3+

a2x2+a1x+a0

(30)

(31)

式(30)中的常数a0、a5由式(31)确定。

车辆纵向运动参考速度为：

Vref(X)=v0+fzsin(z3(X))

(32)

式中：Vref表示参考速度；v0表示车辆初始速度；fz表示速度幅值；z3(X)表示与纵向位移有关的函数。

为了验证本文设计的横纵向联合跟踪控制器的有效性和鲁棒性，设置3种不同初始车速下的横向和纵向工况下的跟踪能力。

从上述仿真结果可以看出，车辆在不同工况下的横纵向跟踪控制能力基本上可以跟踪上期望的轨迹。图3～5表示车辆在不同车速下的横向跟踪性能。从图3、4中可看出，控制器能够使车辆在不同车速下基本上按照期望的换道轨迹行驶。

图3 车辆横向位移

图4 车辆航向角

图5为车辆在不同车速下的横向跟踪误差，随着车速的增加其跟踪效果下降，但从图中可看出车辆在108 km/h的车速下横向跟踪误差在0.05 m范围内，控制器的横向跟踪性能较好。

图5 车辆横向跟踪误差

图6、7表示车辆的纵向跟踪性能，其中图6设置了3种不同的速度参考轨迹，车辆能够较好地跟踪上期望的速度轨迹。

图7表示车辆在3种速度下的跟踪误差，从图中可以看出控制器在72 km/h和90 km/h状态下跟踪误差都在0.5 km/h内，但随着速度继续增加，在108 km/h的速度跟踪误差达到了1 km/h，表明控制器的跟踪效果随着速度增加变差。

图8和图9表示车辆在不同车速下的前轮转角和加速度变化。

图9 车辆加速度变化

从图6中可以得出，随车速提高，前轮转角变化幅度随之增大，在108 km/h的速度下，前轮转角的变化也在0.6°以内，车辆能够稳定行驶；从图9可以看出加速度的变化随着车速增加变化范围为从78 km/h速度下的[-1 1]增加到了108 km/h速度下的[-2.2 2]，表明其跟踪性能随着速度增加而下降。结合控制器的横纵向跟踪性能可以得出，该控制器基本上能够较好地跟踪期望轨迹，但其高速的跟踪性能低于低速的跟踪性能。

5 结论

考虑到多数研究只针对换道过程中车辆横向位置变化设计了跟踪控制器，而没有考虑到纵向速度变化带来的影响，本文以MPC算法为基础，设计了横向路径跟踪与纵向速度跟踪的控制器，将3自由度车辆模型和点质量模型相结合，在通过前轮转角对车辆换道进行横向控制的同时考虑车辆的纵向运动带来的影响，并将加速度作为控制量控制纵向运动，为了减少控制器在运行过程中的复杂度和保证模型稳定性，对模型中的非线性部分进行了线性化和离散化，最后使用二次规划求解目标函数。在仿真环节，设计了72、90、108 km/h 3种速度的仿真工况对控制器的效果进行验证，结果表明：控制横向跟踪误差在 0.04 m内，控制器能较好地跟踪期望轨迹，速度跟踪误差在1 km/h内，前轮转角增幅在0.6°内，变化较为平缓，汽车能够稳定行驶，加速度变化范围随着车速提高也有所增大，其变化范围为[-2.2 2],虽然高速下的跟踪效果有所下降，但仍符合预期。仿真结果表明：本文设计的横纵向联合跟踪控制器在横向和纵向控制上有较好的有效性和鲁棒性。