基于局部模糊聚类的超像素分割算法
2021-12-14龙建武陈鸿发鄢泽然朱江洲
龙建武,陈鸿发,鄢泽然,朱江洲
(重庆理工大学 计算机科学与工程学院, 重庆 400054)
图像是有效传递信息的主要方式之一,良好的分割算法能为图像理解带来巨大的帮助。Ren等[1]首次提出了超像素的概念,超像素分割是将图像划分成具有一定视觉感知意义的原子区域,每个区域内的像素具有高度的相似性,从而提供一种简明的图像表示形式。超像素显著地降低了图像后续处理的复杂度,提高了处理效率。超像素分割正逐步成为越来越受欢迎的图像预处理技术,被广泛用于图像分割[2-3]、目标识别[4]、目标追踪[5]、3D重建[6-7]等众多计算机视觉任务中。直至目前,为生成良好的超像素以满足各种视觉任务的需要,已有多种超像素分割算法相继被提出,根据原理的不同主要分为两类。第一类是基于图论的能量优化方法,比如规则化图割算法[8](normalized cuts,NCuts)、熵率算法[9](entropy rate superpixel,ERS)、懒惰随机游走算法[10](lazy random walk,LRW)。最初Shi等[8]提出的NCuts方法能生成具有良好边界粘合和规则形状的超像素,然而归一化割是计算密集型的,每一次迭代只能产生一个超像素,因此NCuts的计算复杂性非常高。Liu等[9]提出的基于熵率的超像素分割算法(ERS)将超像素分割问题表述为一个目标函数,该函数由一个图和一个平衡项组成,即计算从图上的削减成本到生成超像素的熵率。熵率可以帮助将紧凑和均匀的区域组合在一起,这也有利于超像素覆盖一个关于感知边界的单一对象,但是ERS超像素的形状不够规则。Shen等[10]提出的懒惰随机游走算法(LRW)是从输入图像中获取每个像素的概率,并使用概率和切换时间获取初始超像素。LRW引入了新的能量函数,迭代优化初始超像素,但是该方法的分割效率不佳。第二类是基于聚类的特征优化方法,包括简单线性迭代聚类算法[11](simple linear iterative clustering,SLIC),线性谱聚类算法[12-13](linear spectral clustering,LSC),实时DBSCAN聚类算法[14](real-time DBSCAN clustering,DBSCAN)。Achanta等[11]于2012年提出的简单线性迭代聚类(SLIC)采用K均值聚类方法生成相对较低计算成本的超像素,但面对复杂图像时不能很好地贴合目标对象边界。Shen等[14]提出了基于密度的带噪声应用空间聚类DBSCAN算法用于超像素分割,DBSCAN算法分为2个阶段:在第一个阶段,使用DBSCAN将像素聚类成超像素;在第二阶段,将小的超像素合并到大的超像素中。该算法具有O(N)的计算复杂度,表现出了非常好的实时性。Li等[12-13]采用的线性谱聚类提取超像素结合了归一化切割和K均值的优点,能获得良好质量的超像素。然而,由于计算特征比较复杂,LSC的计算复杂度高。近两年,一些新的超像素分割算法相继被提出,包括高斯混合模型超像素算法[15]( gaussian mixture model superpixel.GMMS)和动态随机游走算法[16](dynamic random walk,DRW),它们拥有着良好的算法性能,但同时也存在着不足之处。
虽然上述方法各具优势,但一直以来提出一种实时的、边界贴合与规则性相适应的、超像素数目与迭代次数可控的、算法复杂度较低的超像素分割算法都是一个非常具有挑战性的研究问题。通过上述分析,以往的超像素分割算法大部分都是通过设计不同的能量优化函数进行硬划分,对于简单图像能够得到很好的效果,但在处理复杂图像时分割效果不尽如人意,或者是采用的能量优化函数包含的特征较多导致算法复杂度较高,因此如何保证算法复杂度与分割效果两者之间的平衡是值得深入研究的问题。为满足这些要求,本文提出一种基于局部模糊聚类的超像素分割算法,这是FCM算法首次应用于超像素分割。超像素用于代替像素进行更紧凑的视觉表示,并作为大量图像处理应用的一个重要的预处理步骤,它的计算成本是最受关注的问题之一。在这些超像素算法中,SLIC算法、DBSCAN算法等已成为较为流行的算法,因为它可以在不耗费太多成本的情况下快速生成超像素,但其仍有许多空间可提高。一种理想的超像素方法不仅需要满足良好边界粘附的要求,而且还需要高效。由于在视觉应用中使用了超像素分割作为预处理步骤,所以优先选择具有较少计算的高质量超像素分割算法。本文提出的局部FCM超像素分割算法继承了现有算法比如SLIC、DBSCAN等的优点,并进一步提高了分割效果。本文中将FCM算法用于生成超像素,由于FCM算法是以隶属度的形式对图像进行软化分,它能有效减小复杂图像中的复杂纹理对分割带来的影响,以及对图像中不规则对象的细分也能达到更好的效果。为了更好地利用FCM算法生成性能优良的超像素,对算法的搜索区域进行了几何限制,同时结合超像素的特点,缩小了隶属度的计算区域,改进了FCM算法的初始化方法与聚类中心的更新方式。生成超像素的过程主要分为两步,首先通过FCM聚类算法获得初始超像素,在该步骤中,聚类中心的更新改为每个超像素的所有像素点向量平均值,这满足了超像素的规则度的要求。隶属度矩阵由像素的所属3×3邻域超像素的隶属度组成,而隶属度计算中包含了像素点与各个聚类中心的向量距离加权。然后,通过颜色和空间信息的测量,将初始的小超像素与其附近的超像素融合在一起。
1 相关方法
1.1 SLIC算法
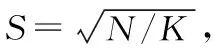
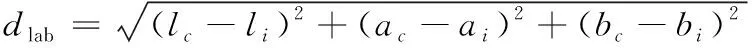
(1)
(2)
D=dlab+(m/S)dxy
(3)
最后可能出现一些“孤立”超像素,这就需要将“孤立”超像素合并到与邻近超像素距离度量最小的超像素中,以保证超像素块的一致性。整个过程如算法1所示。
算法1 SLIC算法
输入:包含N个像素点的图像I
输出:SLIC超像素分割结果
初始化:超像素个数K以及K个像素点作为聚类中心,并将中心移动到邻域内梯度值最小的像素点处。设定迭代停止阈值E,初始化聚类中心ci,设置迭代计数器t=0。
算法开始:
1:对N个像素计算在搜索范围内的到聚类中心点的距离,并将该像素点归入距离最近的聚类。
2:对K个聚类中心点进行更新。
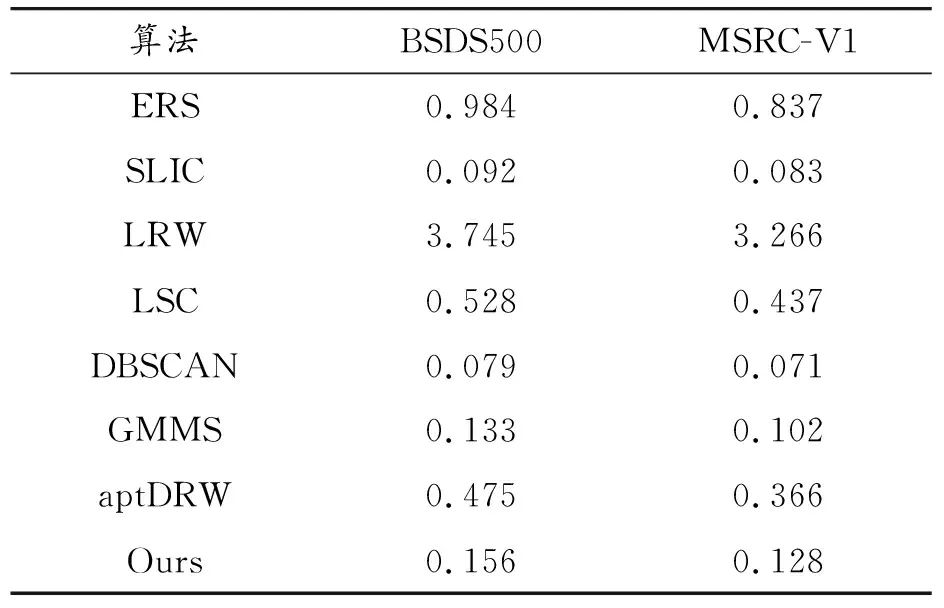
3:如果‖ct-ct+1‖ 4:将“孤立”超像素进行合并。 算法结束 模糊C均值(FCM)算法是一种基于软化分的聚类算法。FCM算法的目标价值函数为: (4) 式中:uij∈[0,1];m是控制聚类效果的参数;ci是模糊簇的聚类中心;dij表示第j个数据点与第i个聚类中心的欧式距离。然后构造带有约束因子的拉格朗日函数: (5) 式中:λj是n个约束式的拉格朗日乘子。对式子中uij求导,得到使目标价值函数最小的必要条件: (6) (7) 通过迭代更新隶属度与聚类中心,当目标价值函数几乎达到最小时,获得聚类结果。整个过程如算法2所示。 算法2FCM算法 输入:数据样本 输出:数据聚类结果 初始化:给定聚类类别数c,0 算法开始: 1:根据式(6)计算或更新隶属度矩阵uij。 2:根据式(7)更新聚类中心ci。 3:如果‖ct-ct+1‖ 算法结束 传统FCM算法通过计算隶属度的形式来确定每一个数据点属于某个聚类的程度,它的优点是,对于满足正态分布的数据聚类效果会很好。算法是收敛的,因此得到的模糊隶属度矩阵具有一致性;它的缺点是,当数据中包含噪声的时候,聚类效果不好。算法的性能很依赖于初始聚类中心,同时算法是基于全局数据,当数据量特别大时,整个算法就非常耗时,效率低。 针对以上问题,一些典型的改进模糊聚类方法被提出,比如,PCM算法[17]作为一种穷举型搜索算法,通过改变隶属度的约束条件来改善聚类效果,它能很好地处理噪音,从而弥补了FCM容易受噪声影响的不足。但PCM 算法需要一个比较好的初始划分,以确保准确的聚类,这是一个难解决的问题;AFCM算法[18]通过对度量方式进行非线性变化,从某种程度上改善了聚类结果,但算法变得更加复杂,这种改变度量方式得到的聚类算法在数据尺度发生改变的时候,会比较敏感,可能会导致很糟糕的聚类结果,所以其适用性并不广泛;Wang等[19]提出了一种使聚类中心的搜索范围限制在直方图峰值附近的新的FCM算法,该算法加快了收敛速度,但是它仅仅适用于有明显峰值的聚类样本;反之,则不适用。从以上分析可以看出,这些改进的模糊聚类算法各具优点,但同时也存在着许多不足之处,因此,对模糊聚类算法提出更好的改进是非常有必要的。 根据在分割过程中,优化围绕种子点像素搜索相邻像素的搜索策略,利用FCM对复杂图像的像素以隶属度的形式进行聚类,提出了一种基于局部模糊聚类的超像素分割算法。传统意义上的FCM算法的搜索方式是基于全局的,其搜索区域如图1所示,并且聚类中心的更新也是基于全局的,对于图像这种包含大量像素点的数据来说,相应的计算复杂度非常高,效率也非常低。所以为了与对图像进行超像素分割相适应,需要对传统的模糊聚类算法进行改进。Lab颜色模型由3个要素组成,L表示亮度,a表示的颜色通道的范围是从绿到红,b表示的颜色通道的范围是从蓝到黄。Lab颜色模型优点在于色域宽阔,包含了RGB颜色模型的所有色域,同时弥补了RGB色彩分布不均的不足。由于在超像素分割过程中需要充分利用像素的颜色信息,所以需要尽量保留宽阔的色域来获得更完整的颜色信息。而Lab颜色模型能够很好地符合上述要求,这对在超像素分割过程中提升分割效果有显著的作用,因此本文算法选择CIELAB颜色模型。聚类过程从在步长为S的常规网格空间上采样K个聚类中心Ci=[li,ai,bi,xi,yi]T的初始化步骤开始,生成大小相等的超像素,聚类中心处于与该区域像素向量的平均值相对应的位置。这样做可以有效避免将超像素种子点设定在边缘并且减少噪声像素成为超像素种子点的机会。在图像中,当每个像素周围的邻域像素离该像素越近时,他们之间的相似性就越高,这种分布特点与正态分布的特点比较相似,根据前文中提及的模糊聚类算法对满足正态分布的像素点的聚类效果会很好的优点,并且考虑到每个像素周围的邻域超像素包含了相应数量的像素点,而3×3邻域大小能够较好地覆盖一定邻域内的像素,在保证覆盖邻域内像素的同时避免了像素间差异性过大。因为邻域过小比如4邻域就不能完全覆盖邻域内像素,邻域过大比如5×5邻域会产生邻域内像素间差异性过大的影响,两者都会使分割不够准确,不利于算法的性能。为了最终获得更好的超像素分割结果,本文算法分配每个像素与被划分的3×3邻域的超像素相关联,改进后的搜索区域如图2所示。这是加快算法速度的关键,因为限制搜索区域的大小会大大减少计算的次数,降低计算复杂度。限制搜索区域大小的先验信息为超像素个数K值。当K值过大时,每个超像素区域就非常小,对应搜索区域就很小,不能很好的保证信息的完整性;当K值过小时,每个超像素区域就很大,对应搜索区域就很大,此时像素信息过于冗余,会导致划分结果不够准确,降低分割效果。所以整个过程需要合理地初始化K值来限制搜索区域的大小。 图1 FCM算法的搜索区域示意图 图2 本文算法的搜索区域示意图 此处引入FCM算法中隶属度函数的概念来计算像素对周围3×3邻域的超像素的隶属度u,然后构造与超像素分割相适应的带有约束因子的拉格朗日函数: (8) 式中:n代表搜索区域内的像素个数,同时: dij=dc+ds (9) 其中: (10) (11) 对u和c分别进行求导得到使目标函数J达到最小的必要条件: (12) (13) 在实现算法的过程中,首先利用初始化的超像素求像素平均值计算聚类中心,然后确定d,接下来利用式(12)(13)进行迭代更新,直到聚类中心几乎不再改变,可利用式(14)来控制: |Jt+1-Jt| (14) 式中:t是算法迭代次数;E是迭代停止阈值。t与E是给定值以满足算法达到分割效果的要求。像其他超像素算法一样,FCM超像素没有显式强制连接,在聚类过程结束时,一些不属于与其聚类中心的“孤立”超像素可能仍然存在。为了解决这一点,这些超像素被指定为最近的聚类中心的标签。在合并过程中,利用距离函数D计算“孤立”超像素与邻近超像素之间的距离,距离函数D中包含了颜色距离和空间距离。一个好的超像素不仅要通过将超像素的边界贴合在物体边缘的性能来衡量,而且也能保持超像素的均匀大小,本算法利用色差来确定2个初始超像素是否应该合并为一个,空间距离保证了最终超像素的规则性,那么合并距离D被定义为: D(Ii,p)=α1dc(Ii,p)+(1-α1)ds(Ii,p) (15) 其中: (16) (17) 算法3基于局部模糊聚类的超像素分割算法 输入:图像I 输出:超像素分割结果 初始化:指定超像素个数K,初始化聚类中心c,设定迭代停止阈值E,搜索步长S,设置迭代计数器t=0。 算法开始: 1:在搜索区域内根据式(12)计算或更新隶属度矩阵uij。 2:根据式(13)更新聚类中心ci。 3:如果‖Jt-J(t+1)‖ 4:根据式(15)对“孤立”超像素合并到邻近超像素区域内得到最终的划分结果。 算法结束 由于在进行超像素合并时需要同时考虑到颜色信息和空间信息,相比于典型的距离度量方式如传统欧式距离、马氏距离以及曼哈顿距离等,本文算法在超像素合并步骤采用的距离度量方式的特点在于,综合考虑了颜色信息和空间信息,以每个超像素的聚类中心的颜色信息和空间信息代表对应的超像素,将颜色距离和空间距离相结合,并各自赋予相应的权重,颜色距离权重用来控制颜色信息的相似性,空间距离权重用来控制空间信息的影响。而此时对颜色信息的依赖性比对空间信息的依赖性要大,因此赋予较大的颜色距离权重和较小的空间距离权重,这样可以保证两者之间的平衡,从而在比较准确地衡量“孤立”超像素和邻近超像素相似性的同时还能够保证合并后的最终超像素的规则性。综上,该距离度量方式优点在于,能够很好地衡量“孤立”超像素和邻近超像素的相似性,确保是否应该合并成一个,同时保证了最终超像素的规则性,这符合生成良好超像素的目标。 为验证本文算法的有效性,与现有典型超像素分割算法如ERS算法、SLIC 算法、LRW算法、LSC算法和DBSCAN算法以及近两年一些新提出的超像素分割算法如GMMS算法和aptDRW算法从视觉、分割精度[20]和实时性等方面进行量化对比。 为了定量评价本文超像素分割算法的性能,实验中选择 BSDS500和MSRC-V1 2个数据集。BSDSS500是用于边界检测和图像分割的数据集,内容包括从户外场景、景观、建筑、动物到人类。它由500张图片组成,包括200张训练图片、100张验证图片和200张测试图片,该数据集中每张图片的大小为321×481或481×321。MSRC-V1是用于目标识别和图像分割的数据集,内容包括建筑、景观和动物等9个类别,总共240张图片。 在对图像进行超像素分割中,高分割精度是最关键和最基本的要求。本文采用常用的准确性定量比较指标,包括边界召回率(BR,boundary recall)和欠分割误差(UE,under-segmentation error)。 边界召回率BR是衡量超像素算法中边界粘附性能的重要指标。边缘召回率BR定义为与超像素边缘的距离小于2像素的真实边缘在所有真实边缘中所占的比例,边缘召回率越高,意味着很少有真正的边界被忽略。边界召回率BR的计算公式如下: (18) 式中:B(si)和B(gj)分别表示超像素边界和GroundTruth(GT)边界的像素集;1()是一个指示函数,用来检查B(si)和B(gj)之间最近像素是否在像素的ε-距离内,并设置ε为2。 欠分割误差UE是边界粘附的另一个评估指标。它是基于每个超像素只属于一个对象的要求。UE测量从GT泄露的超像素内部像素的百分比,如果超像素与多个GroundTruth段有效重叠,UE将相应增加。欠分割误差UE的计算公式如下: (19) 式中:指标函数1( )等于有效重叠的一个值,κ=0.05是阈值。 对比试验所采用的实验平台为1台具有Intel i7-7700HQ 2.80 GHz处理器和8 GB RAM内存的计算机。为了对比公平,实验使用各个超像素分割算法论文给出的源代码,并尽量在不改变算法默认参数的条件下进行。本文算法采用 C++编写。源代码以C++实现的算法还有NC、SLIC、LRW算法,而LSC、ERS、DBSCAN、GMMS、aptDRW算法是以C++与Matlab相结合进行实现的。 各个超像素分割算法在K=300左右时的一些分割结果视觉上的对比如图3所示。取部分结果的一些细节作对比,如图4所示。由图3和图4可知当超像素个数K=300左右时,本文算法得到的超像素形状规则且大小比较均匀,而且边缘附着性能与规则度相对平衡。SLIC算法、LRW算法与本文算法的相似之处在于得到的超像素形状也较为规则。而ERS算法、LSC算法、DBSCAN算法得到的超像素形状总体上没有本文算法规则。比如ERS算法得到的超像素形状不够规则且大小不均匀;LSC算法在图像简单区域得到的超像素比较规则,但是在比较复杂区域得到的超像素形状的规则性不足,DBSCAN算法在图像简单区域得到的超像素的形状呈菱形,但在图像复杂区域得到的超像素规则性欠佳。GMMS算法得到的超像素规则度不够高,而aptDRW算法生成的超像素的大小差异性比较明显。 图3 各超像素分割结果(从上到下各行依次是ERS、SLIC、LRW、LSC、DBSCAN、GMMS、aptDRW、Ours) 图4 超像素局部放大区域的实验结果 由于2个数据集中的图片分辨率相对较小,参考文献[14],实验对比时超像素个数K的值给定范围为100~600。本文算法与各个超像素分割算法的在2个不同数据集表现的性能如下: 各个超像素分割算法在BSD500上的性能曲线如图5、6所示。 图5 边界召回率曲线 图6 欠分割误差曲线 当K=400左右时,各个算法的BR与UE都比较接近。为了能更清楚明了的进行分析对比,本文给出下列相应的实验数据,如表1所示。 表1 BSD500分割结果的BR与UE实验数据 对于各个超像素分割算法在MSRC-V1数据集上的分割性能,本文取超像素个数K=200、400和600时的实验数据进行对比,如表2和表3所示。 表2 MSRC-V1分割结果的BR实验数据 表3 MSRC-V1分割结果的UE实验数据 由于SLIC、LSC、DBSCAN、GMMS和本文算法的算法复杂度均为O(N),根据文献[13-15],超像素个数K=100到600范围内的取值对实时性数据影响不大,而ERS、LRW、aptDRW算法复杂度均高于O(N)。因此取超像素个数K=400时各个算法在BSDS500和MSRC-V12个数据集上的实时性数据进行对比,如表4所示。 表4 K=400时各个算法的平均时间 s 由图5、6和表1~3分析对比可以得出,在2个数据集上,无论是在边界召回率BR还是欠分割误差UE上,本文算法相对SLIC和LRW算法都有明显的优势。这是由于局部模糊聚类采用在3×3邻域超像素搜索区域内计算像素隶属度并比较隶属度大小进行软化分,比较准确地将像素划分到邻域超像素。相比于除SLIC,LRW外的其他超像素分割算法如ERS、LSC、DBSCAN、GMMS以及aptDRW等算法,当超像素的个数设置较少时,本文算法的BR和UE表现欠佳。当超像素个数较多,特别是K=400左右或者K>400时,对于BSDS500数据集,在BR上本文算法比其他算法都略高。在UE上,本文算法比ERS、LSC、DBSCAN和aptDRW算法略低,但略高于GMMS算法;对于MSRC-V1数据集,在BR上,本文算法比其他算法都略高。在UE上,本文算法与ERS、LSC、DBSCAN和aptDRW算法都比较接近,略高于GMMS算法,但在K=600左右时本文算法最低;因此可以得出,本文算法能够较好地处理不同数据集图片。从局部模糊聚类来看,这是因为当超像素个数较多时,超像素区域的像素数量适中,区域像素求平均得到的聚类中心能够很好地代表该超像素,因此能比较准确地在3×3邻域超像素搜索区域内计算像素隶属度并进行划分。同时,在本文算法的合并步骤中,采用距离度量方式能够保证生成的最终超像素的精度。在实时性方面,本文超像素分割算法由于限制了搜索区域的大小,在3×3邻域超像素搜索区域内计算像素隶属度,这表示,在搜索区域内,只需要计算每个像素对于3×3邻域超像素的隶属度,然后通过比较隶属度的大小来进行像素的划分,相比于基于全局的方式,这极大地降低了运算复杂度。与其他超像素分割算法的实时性数据相比较,由表4分析对比可以得出,本文算法慢于实时性最优的DBSCAN及SLIC算法,但相差不大,与GMMS算法也比较接近。而本文算法的实时性相比于ERS、LRW、LSC、aptDRW算法有明显的优势。因此本文算法以良好的实时性获得了较好的分割效果,保证了算法复杂度和分割效果之间的平衡。 本文局部模糊聚类算法对于超像素个数K值的选取比较敏感,因为它决定了聚类中心的初始化,以及之后像素隶属度的计算并进行划分的的准确性。相对于传统FCM基于全局的搜索方式,本文算法大大缩小了搜索区域,有效地降低了运算复杂度,同时不容易受噪声影响,稳定性较高,弥补了传统FCM对噪声比较敏感的不足。 提出了一种基于局部模糊聚类的超像素分割算法。FCM超像素分割算法能够生成形状规则性与边界贴合性保持平衡的超像素。首先通过缩小搜索区域,设计像素对于超像素隶属度的邻域大小,适当改变隶属度的计算方式,得到一种新的基于局部模糊聚类算法,然后利用该算法迭代生成初始的超像素,在后处理步骤中将一些未被划分的像素与邻近超像素进行合并,得到最后的超像素分割结果。采用2种标准的超像素分割精度的评价指标与其他几种经典算法进行比较。本文算法的优势在于对包括复杂对象或复杂纹理区域的图像生成的超像素也能保持良好的形状规则性与边界贴合性,不足在于超像素的分割效果比较依赖于超像素的个数,当超像素个数较少时,本文算法的分割精度不高,这也是本文算法需要解决的问题,需要进一步研究。1.2 传统模糊聚类算法
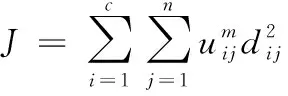
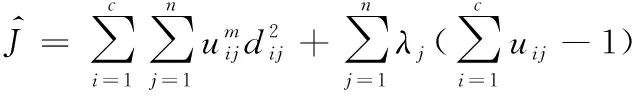
2 本文算法

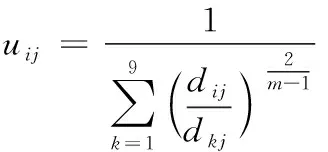


3 实验结果与分析
3.1 数据集
3.2 评价标准
3.3 实验环境
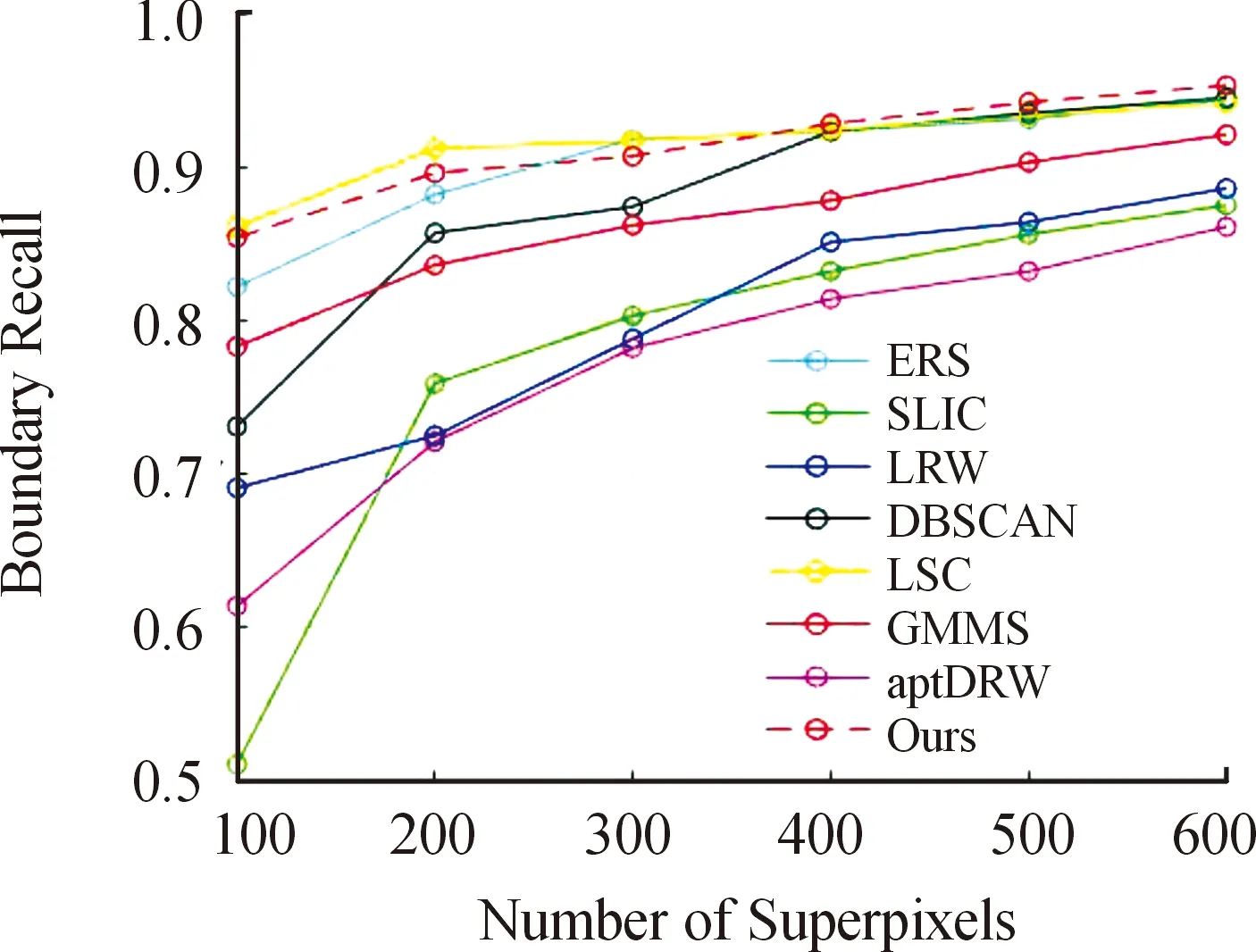
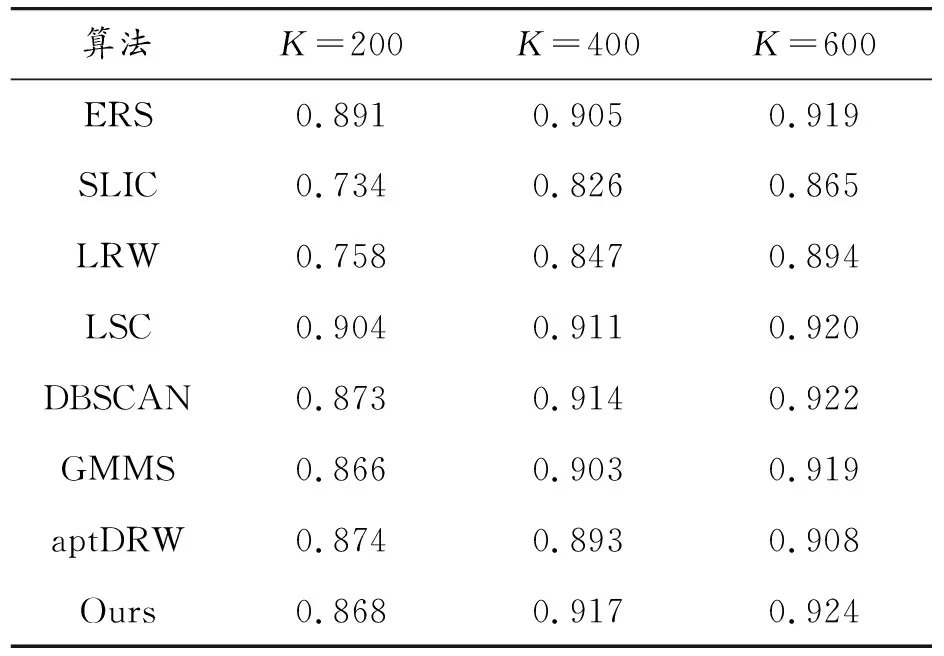
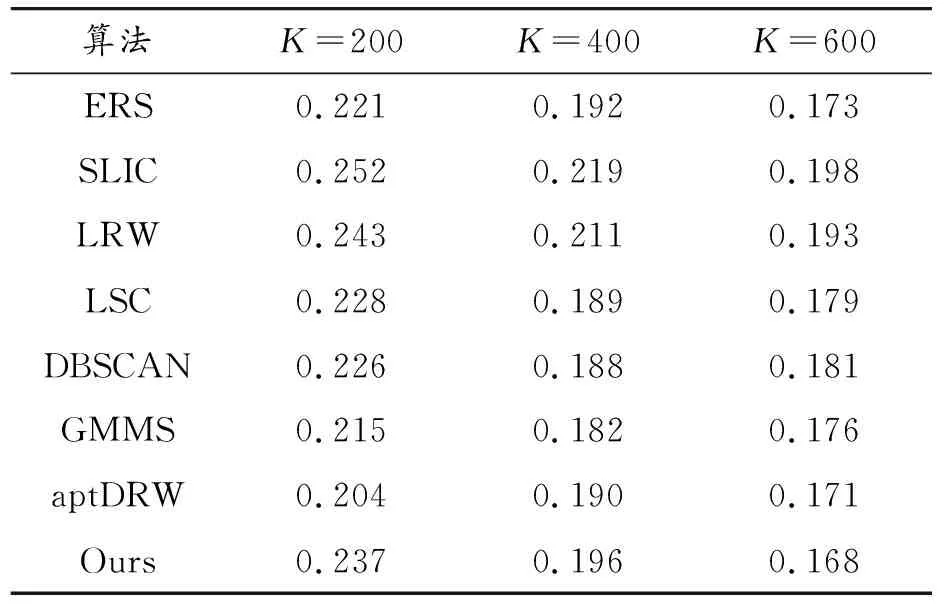
3.4 超像素分割结果比较




4 结论
