升力体外形布局参数对横侧向耦合稳定性的影响分析

张青青, 张石玉, 赵俊波, 赵力宁

(中国航天空气动力技术研究院, 北京 100074)

引 言

世界各军事强国都加紧发展高超声速机动飞行器, 该类飞行器具有打击范围大、 作战响应快、 突防能力强等优点, 可实现大范围机动、 宽速域、 大空域飞行, 处于高超声速武器装备发展的技术前沿. 目前, 我国高超声速飞行器存在耦合效应强、 操控难度大、 极易失控等问题, 制约高超声速飞行器机动范围、 操控性能等总体性能提升.

HTV-2于2010和2011年两次飞行试验均告失败. 分析得出失败原因之一是, 出现了滚转/偏航耦合运动, 诱导的超调偏航/滚转力矩远远超过了实际可控能力, 导致姿态失控[1-5]. 由此可见, 研究高超声速飞行的参数耦合效应问题, 对实现再入飞行器大范围机动和稳定可控飞行, 提升高超声速武器综合性能具有重要意义.

气动布局是飞行器研制的基础, 布局参数对稳定性的影响研究和对参数耦合效应研究都具有根基性作用, 是宽速域、 大空域再入机动飞行器抗失控设计的重要研究内容.

本文基于CST外形参数化建模方法和高速气动特性快速分析方法, 结合科学试验设计及结果分析方法, 研究了升力体外形布局参数对横侧向耦合稳定性的影响规律.

1 外形参数化建模方法

飞行器几何外形参数化建模是布局参数影响分析的第一步, 可对某一类型布局飞行器的气动特性规律开展研究, 从而探索其普适性规律, 也可以有效提高飞行器气动布局设计效率.

本文采用一种基于类别/形状函数描述形式的解析气动外形建模方法(class shape transformation, CST)[6-11]. 该方法通过类型函数和形状函数的乘积实现, 仅需要少量设计变量就能表示较大的设计空间, 具有设计参数少、 适用性强、 建模精度高等特点.

1.1 CST方法的基本原理

CST方法通过一个类型函数和一个形状函数来定义剖面形状. 大多数飞行器外形都可以近似由无数垂直于轴线的截面组合而成. 因此, 引入以下解析截面定义描述形式[12-13]

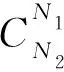
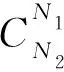
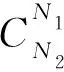
形状函数S(ψ)有多种方法定义, 本文采用n阶Bernstein多项式的加权组合作为S(ψ)的表达形式

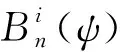
1.2 三维CST描述方法

将基于Bernstein多项式函数定义的形状函数带入截面定义式得到CST截面为

(1)

三维外形可以分解为一系列平行截面沿轴线的组合. 通过在不同轴向位置处使用形状函数描述不同的截面形状, 确定出一个解析形状函数面, 从而得到整个外形的解析描述形式. 采用CST方法将上式中的bi沿轴向展开, 定义

其中,η=x/L, 为归一化的轴线坐标,L为几何外形总长. 带入式(1)并展开， 得

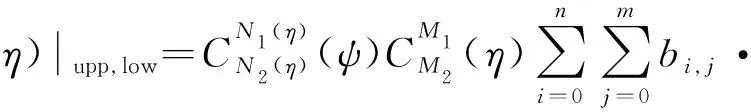
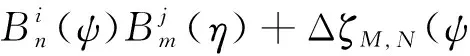
式中,bi,j为飞行器上(下)表面的离散控制权重因子;n为截面侧向控制点展开阶数;m为轴向控制点展开阶数, 此时的表面总控制点数为(n+1)×(m+1); ΔζM,N(ψ,η)为对应(ψ,η)位置处的法向偏心距离修正项.

上述几何外形描述形式也就是在ψ×η的正交二维网格点中设计与其垂直的第三维坐标, 从而表现出三维几何外形特征.ψ和η为单位化坐标, 取值范围在[0,1]×[0,1]之间, 无法描述侧向ψ的范围Y随η的变化. 因此, 对Y方向采用同样的CST控制方式

将上述定义转换到全局坐标系中, 可得到归一化的三维CST外形曲面的表达式

式中,ψ=[0,1]和η=[0,1].

整个三维CST曲面外形的设计参数包括外形尺寸参数和类型函数控制参数具体为: 轴向长度L， 侧向长度Lw； 截面形状控制因子N1(η)和N2(η)， 法向形状控制因子M1和M2， 侧向形状控制因子T1和T2, 表面权重因子bi,j和侧向权重因子bt.当bi,j和bt取1时, 即为最少控制参数情况; 当bi,j和bt为参数矩阵时, 说明在外形表面上分布了对应矩阵维数的控制点. 通过调节bi,j和bt维数, 即可实现控制参数动态增减.

基于上述高还原度CST参数化建模方法, 建立了基于部件组合思想的截面曲线、 外形轮廓及舵面形式的分层描述方法(见图1), 实现了升力体外形的精准建模.

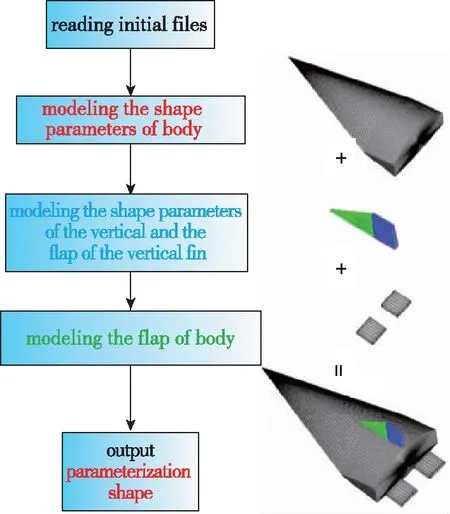
图1 部件组合CST参数化建模流程Fig. 1 Process of CST parametric modeling based on part combination

升力体X-Z平面某截面曲线CST参数化建模及几何绝对误差(见图2)， 图2(a)为X-Z平面原始曲线及CST参数化曲线Z坐标对比， 图2(b)为参数化曲线与原始曲线Z坐标差量放大104后随X坐标变化曲线. 从图2可见， 实际飞行器尺寸的截面曲线误差为10-3m量级.

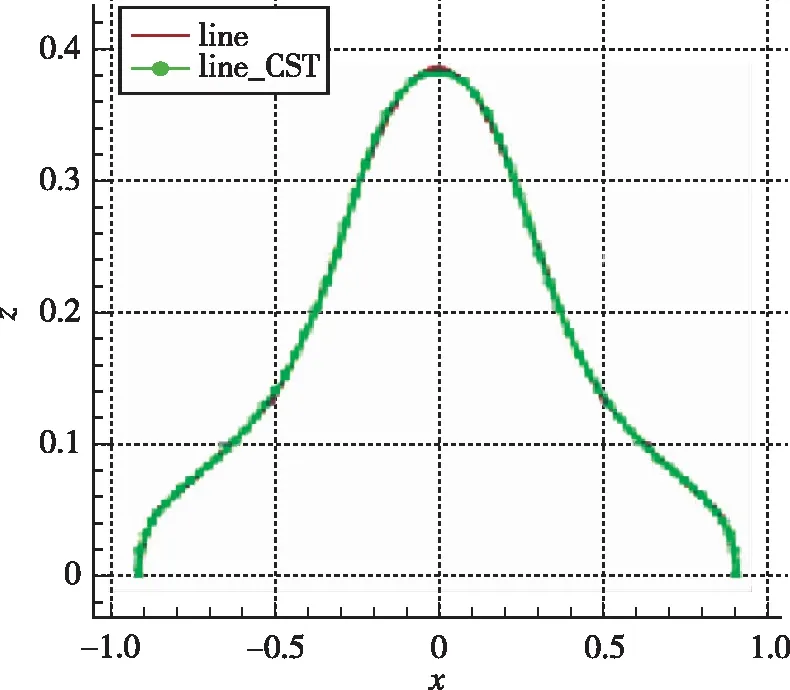
(a) Lines of z～x

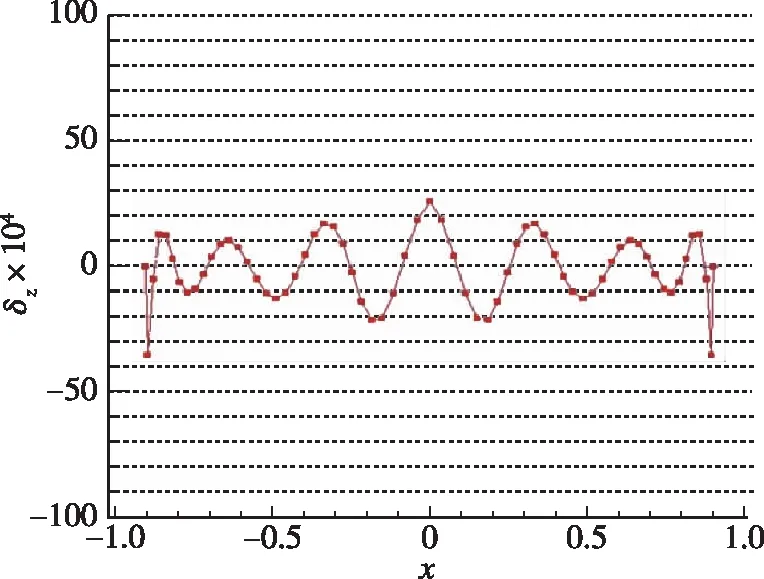
(b) Lines of δz～x图2 截面曲线CST参数化建模及几何绝对误差Fig. 2 Parametric modeling of section curve and geometric absolute error

2 高速气动快速计算方法及可靠性评估

布局参数影响规律分析需要评估大量飞行器外形, 无法采用耗费较多机时的CFD数值计算, 因此选用高效的气动力评估方法.

基于面元碰撞角的气动力计算方法, 计算速度快、 效率高. 切锥法对于超声速及高超声速圆锥体外形、 且在气流碰撞角不大时计算精度较高, 而Newton法则对于大碰撞角情况及高超声速情况计算精度较高. 本文使用了综合切锥法与Newton法的Darhham-Borker方法[14]. 该方法在小攻角下用切锥法, 大攻角下采用Newton法, 是考虑Mach数效应影响的一种工程计算方法. 还引入了基于湍流平板的摩阻计算方法, 增加了摩擦力方向效应的修正. 采用式(2)对底阻进行修正, 提高计算精度.

(2)

式(2)中,Ma∞为自由来流Mach数,Sr为参考面积，Sb为底部面积，Cpbase为底部压力系数，CA为修正后的轴向力系数.

采用本文建立的基于组件的CST参数化建模方法, 对某升力体外形的机体、 垂尾及机体襟翼分别进行了几何外形建模, 并根据安装位置组装为升力体外形(见图3), 外形具体尺寸见下文表1的Baseline列.

以该升力体外形为例, 采用工程估算方法对比了数模与参数化建模外形在Ma=5时的气动力估算误差(见图4), 从图中看出, 参数化建模外形误差小, 可用于规律研究.

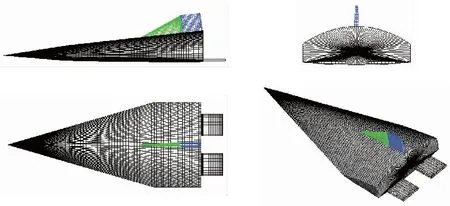
图3 某升力体CST参数化建模外形Fig. 3 Parameterized shape of a lifting body

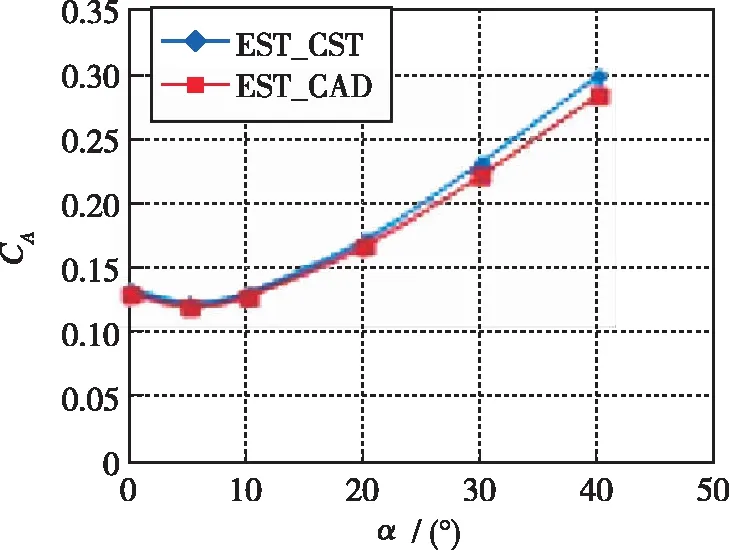
(a) Lines of CA～α

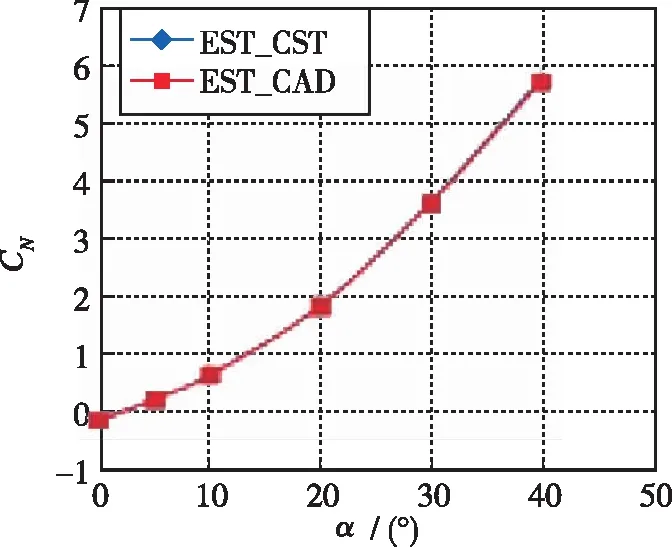
(b) Lines of CN～α

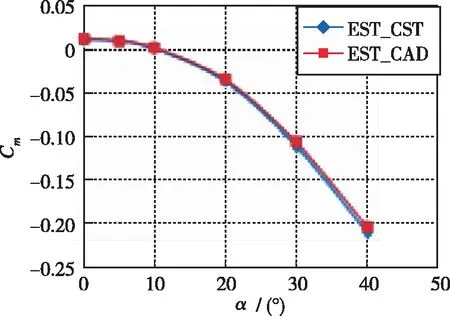
(c)Lines of Cm～α

(d) Lines of CL～α

使用参数化建模外形, 对比了Ma=5时工程估算与CFD计算的升阻比及力矩系数特性(见图5), 同时分析了两种方法得到的耦合稳定性参数(见图6), 从图中可以看出, 开环动态偏离稳定判据Cnβ ,dyn在30°以上攻角误差量值明显增大, 因而该快速计算方法不能代替CFD方法进行外形详细设计阶段耦合稳定特性的定量评估. 但各耦合特性随攻角的变化规律符合得好, 该方法可满足本文规律特性研究需要, 可用于方案设计阶段分析横侧向耦合稳定性影响规律.

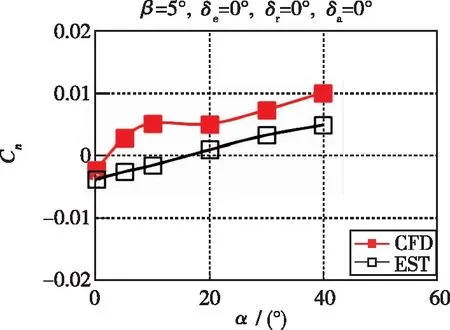
(a) Lines of Cn～α

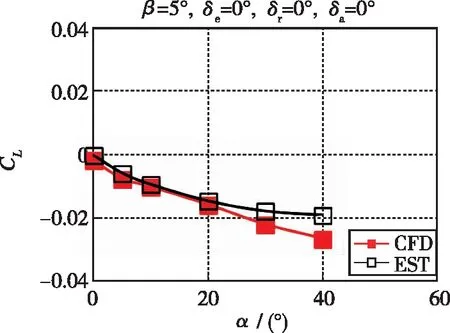
(b) Lines of CL～α

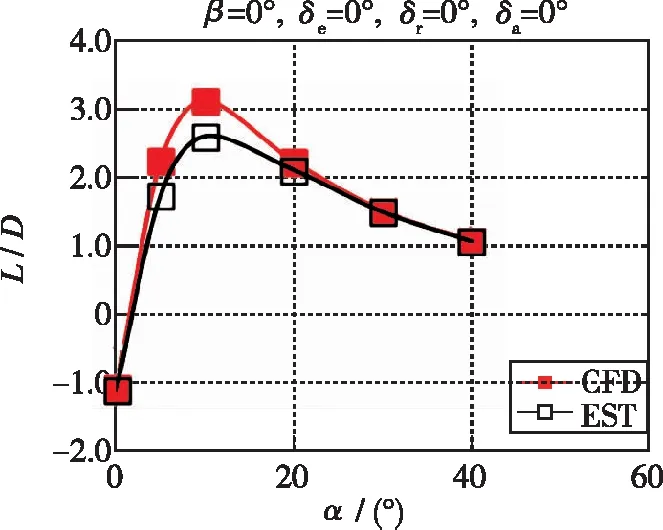
(c) Lines of L/D～α

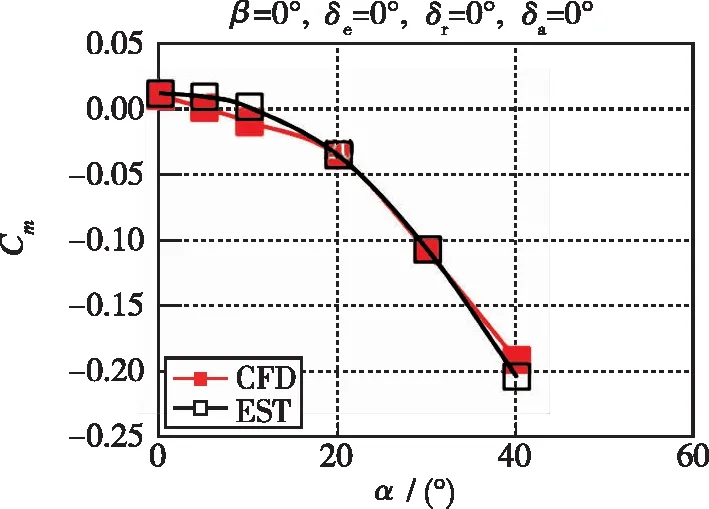
(d) Lines of Cm～α

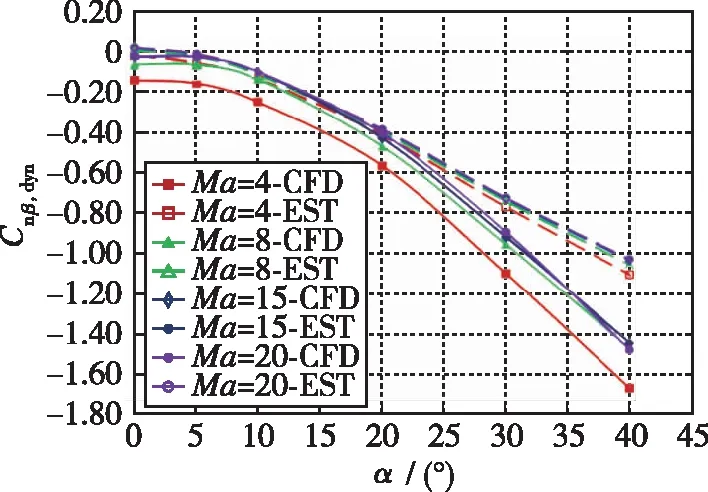
(a) Lines of Cnβ ,dyn～α

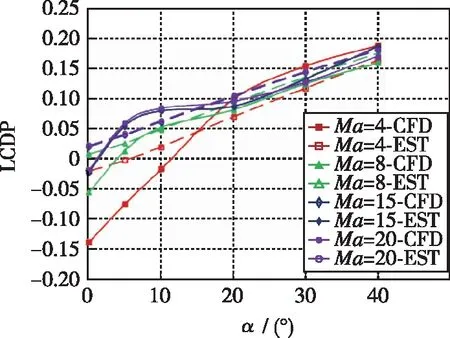
(b) Lines of LDCP～α

(c) Chart of LCDP～Cnβ ,dyn图6 升力体工程估算与CFD计算耦合稳定性对比Fig. 6 Comparison between the estimated values and CFD calculation of the lifting-body′s coupling stability parameters

3 试验设计与分析方法

本文采用试验设计方法, 对设计空间进行探索. 试验设计是研究和处理多因子与响应变量关系的一种科学方法, 通过合理地挑选试验条件, 安排试验, 并通过对试验数据的分析找出输入的多因子和输出的响应变量之间的定性定量关系.

在整个设计空间中选取一定数量的样本, 有效的样本要求尽可能全面地反映设计空间的特性. 具体选用拉丁超立方试验设计方法来取样.

3.1 拉丁超立方方法

拉丁超立方方法是一种充满空间的试验设计, 使输入组合相对均匀地填满整个试验区间, 并且每个试验变量的每个水平只被研究一次[15](见图7). 该方法的本质是控制抽样点位置, 避免抽样点在小邻域内的重合问题, 可以确保产生的样本点代表向量空间中的所有部分.

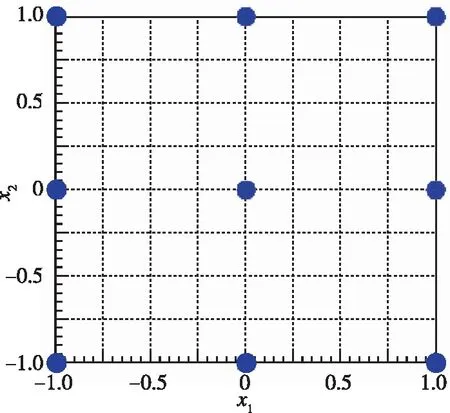
(a) Orthogonal design

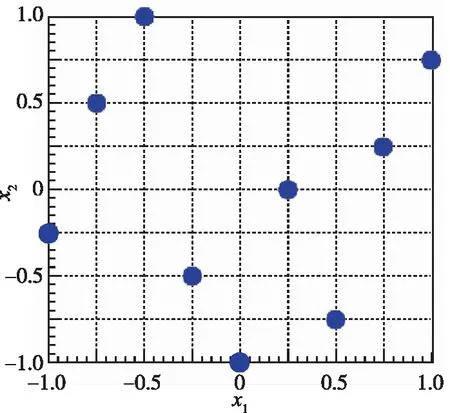
(b) Latin hypercube design图7 正交与拉丁超立方设计对比(9个样本点)Fig. 7 Comparison between the orthogonal design and Latin hypercube design(9 sample points)

拉丁超立方设计方法有相当大的随机性, 即无需考虑问题的维数, 样本的数目可多可少, 可以是任意整数. 该特点符合本文输入变量不同维数的研究需要, 因而采用拉丁超立方方法进行试验设计.

3.2 试验结果分析方法

一定数量的有效样本点可以反映整个设计空间的特性. 根据样本点及样本点上的响应, 主要采用系数表、 Pareto图这两种形式对试验结果进行分析.

(1) 系数表

根据样本点建立多元二次回归模型, 通过系数表进行表达.

系数表反映多项式模型中每一个项对响应的主效应.

(2) Pareto图

Pareto图反映样本拟合后模型中所有项对每个响应贡献程度百分比. 值是系数表normalized值. 蓝色表示正效应, 红色表示反效应.

4 升力体外形耦合稳定性分析

4.1 升力体外形参数选择

本文研究的升力体外形, 与耦合稳定性相关的主要布局参数见图8.

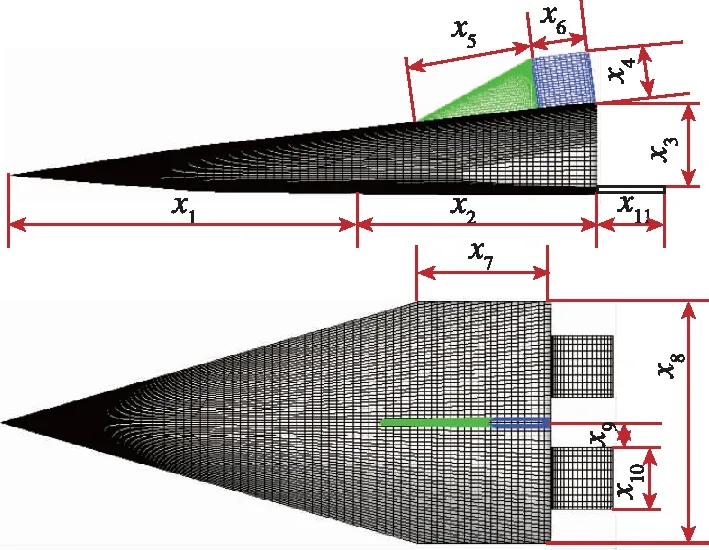
图8 升力体外形参数示意Fig. 8 Geometry parameters of a lifting body

选择11个外形参数来分析横航向耦合稳定性影响规律. 11个长度变量的变化范围均为0.2, 每个参数的上下限及基准值见表1.

表1 升力体外形参数表Table 1 Geometry parameter range of a lifting body

4.2 试验设计结果分析

在11个参数设定的变化空间内, 采用拉丁超立方试验方法设计选取220个样本点, 即计算220个不同的几何外形. 气动分析状态见表2.

表2 气动分析状态Table 2 State of areodynamic analysis on a lifting body

偏航动态稳定性参数Cnβ,dyn在攻角0°, 40°,Ma=5, 15时的系数表线性项见表3. 从表中可看出, 同一攻角下, 随Mach数增大, 系数均有一定程度的减小, 说明随Mach数增大偏航动态稳定性参数绝对值减小.

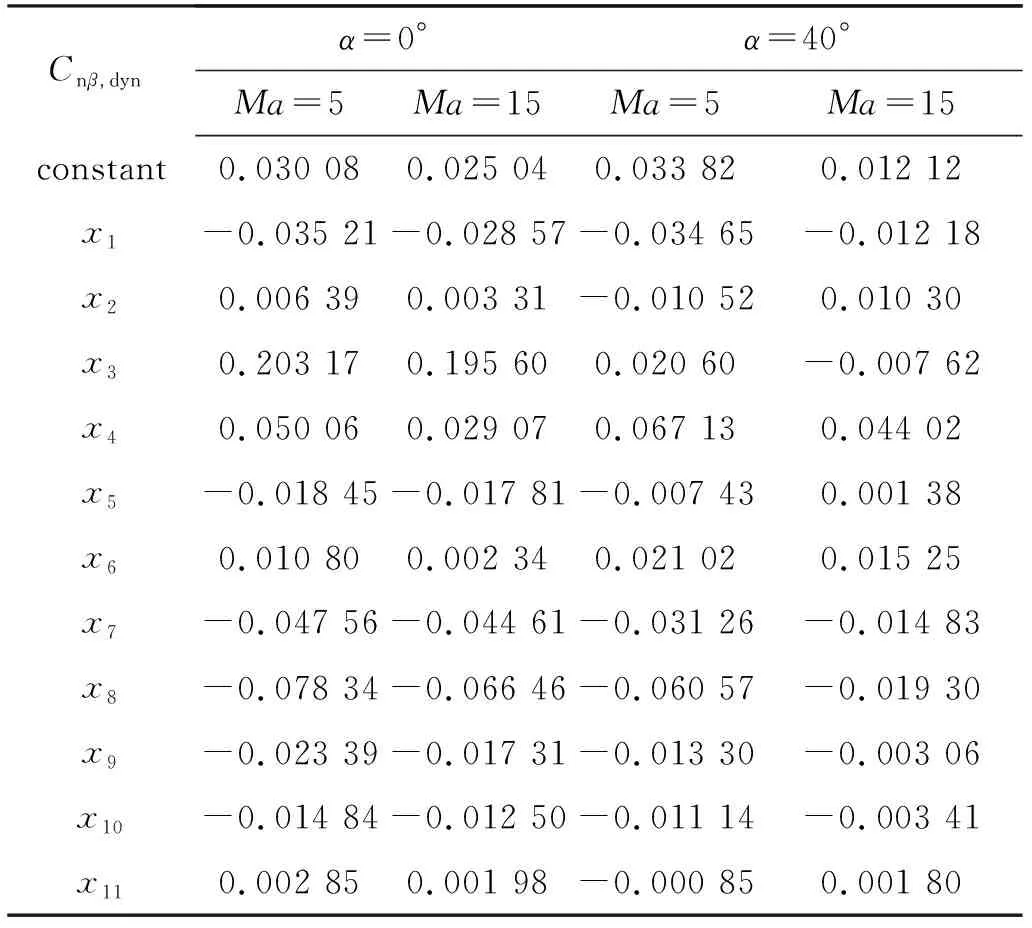
表3 偏航动态稳定性参数Cnβ,dyn系数表线性项Table 3 Linear terms of coefficient table on dynamic directional stability parameter

图9是偏航动态稳定性参数Cnβ,dyn在Ma=5, 15, 攻角0°, 40°的Pareto图.

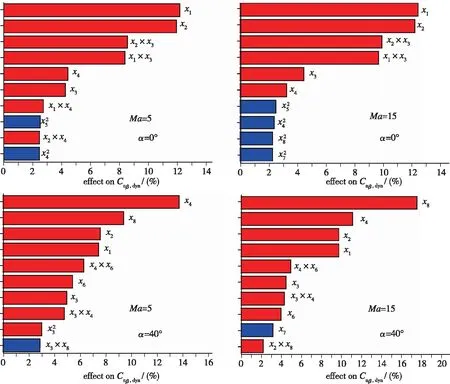
图9 升力体布局参数对Cnβ, dyn影响的Pareto图Fig. 9 Pareto diagram of the influence of lifting-body′s main shape parameters on Cnβ, dyn

从图中可以明显看出, 影响较明显的是机体前半段长x1， 机体后半段长x2， 机体高x3， 垂尾展长x4这4个参数, 且均为负效应. 在40°攻角时, 两个Ma下垂尾展长x4， 机体宽x8， 机体后半段长x2， 机体前半段长x1这4个参数影响较大, 均为负效应.

随着Mach数变化, 主导布局参数变化不明显, 仅各主导布局参数的影响程度量值有变化. 随着攻角变化, 主导布局参数有明显改变. 因而要关注弹道的关键攻角.

横向操纵滚转反逆参数LCDP在Ma=5, 15,α=0°, 40°时的系数表线性项见表4.

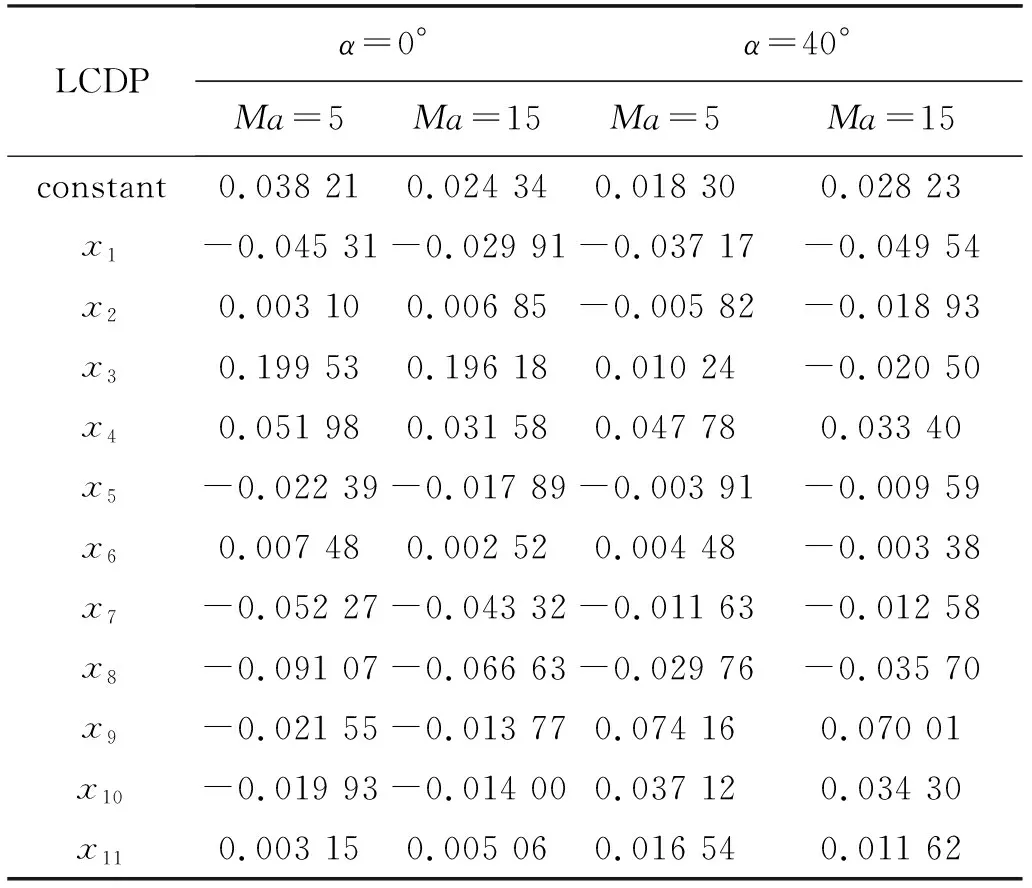
表4 横向操纵滚转反逆参数LCDP系数表线性项Table 4 Linear terms of coefficient table on lateral control departure parameter(LCDP)

横向操纵滚转反逆参数LCDP在Ma=5, 15,α=0°, 40°时的Pareto图见图10. 从图中可以明显看出, 影响明显的是机体前半段长x1， 机体后半段长x2， 机体高x3， 垂尾展长x4这4个主要决定侧视图轮廓的参数, 均为负效应.

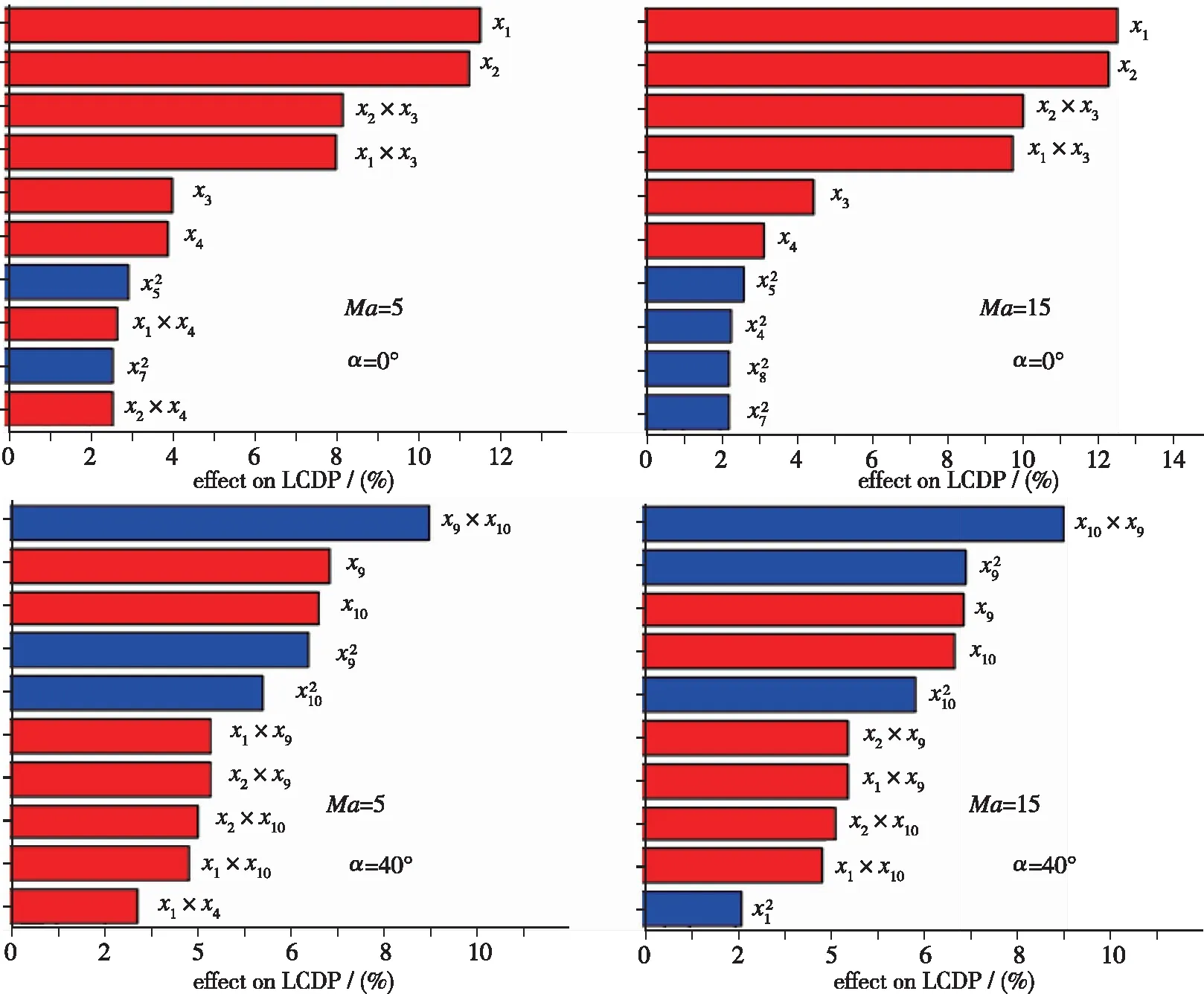
图10 升力体布局参数对LCDP影响的Pareto图Fig. 10 Pareto diagram of the influence of lifting-body′s main shape parameters on LCDP

在40°攻角时, 舵面横向安装位置x9, 舵面展长x10这两个与舵面相关参数的交互项、 线性项、 2阶项对LCDP的影响最大, 线性项为负效应, 其余为正效应. 其次是机体前半段长x1, 机体后半段长x2与舵面横向安装位置x9及机体前半段长x1, 机体后半段长x2与舵面展长x10的交互项, 且都为负效应.

5 结论

本文综合了基于部件组合思想的分层CST外形参数化建模技术、 高速气动特性快速分析方法及拉丁超立方试验设计方法, 形成了高度自动化的布局参数稳定性影响规律分析技术. 针对升力体外形, 深入研究了主要布局参数对横侧向耦合稳定性开环动态偏离稳定判据和闭环横向控制偏离判据的影响规律, 主要结论如下:

(1)部件组合CST外形参数化建模技术适用性强、 建模精度高, 适用于布局参数影响规律分析, 也可用于气动外形优化设计.

(2)对于升力体外形, 高速气动特性快速分析方法计算结果与CFD计算结果变化规律符合较好, 可用于布局参数影响规律分析.

(3)对于耦合稳定性参数, 随着Mach数变化, 横侧向稳定性的主导布局参数变化不明显. 随着攻角变化, 横侧向稳定性的主导布局参数有明显变化. 因而需要重点确定关键攻角.

(4) 影响横向操纵滚转反逆参数LCDP的主导布局参数为非线性影响(包含了2阶项), 主要原因是几何的融合度高.