高速飞行器失控成因及操稳判据发展综述
2021-12-13李华光郑宏涛蔡巧言李贵成
张 静, 李华光, 郑宏涛, 唐 鹏, 蔡巧言, 李贵成
(1. 西北工业大学无人系统技术研究院, 陕西西安 710072; 2. 中国运载火箭技术研究院, 北京 100076;3. 北京航空航天大学交通科学与工程学院, 北京 100083)
引 言
高速飞行器设计工作面临的一个难题是飞行性能和机动能力极大提高的同时, 飞行器失控的危险在增加, 飞行器变得越来越难以操纵. 飞行器耦合问题, 即不同通道之间存在的气动力或惯性力的关联效应, 成为诱发飞行器稳定性偏离、 造成失控的最危险和最重要诱因之一[1-2].
随着高速飞行器的发展, 出现了新的技术跨越和技术特点: (1)突破了传统轴对称基本布局方式, 采用面对称布局, 总体设计复杂化[3]; (2)飞行器设计上要求大升力和低阻力, 实现升阻比远大于1.0, 采用升力式再入, 或吸气动力巡航, 实现大气层内长距离飞行; (3)依靠空气舵面实现对飞行器姿态的操纵和控制, 同时需要适应飞行器在Mach数和高度范围更加广泛的大飞行包线内飞行[4]; (4)扩大飞行包线, 增大了设计的优化空间, 但是由此需要气动、 弹道和控制等系统设计适应各专业综合和复杂的要求, 设计难度显著增加[5-6]; (5)由于机动性的提高, 不可避免存在严重的各种类型的耦合, 处理不好会影响飞行器的设计水平和安全性.
围绕高升阻比高速飞行器的设计, 在提高飞行性能的同时, 还需要同时考虑飞行器的抗失控能力, 这样设计出来的飞行器才是安全和工程上可实现的. 在飞行器设计过程中, 抗失控能力成为与飞行器的性能和机动性同等重要的设计要素. 从某种意义上讲, 高速飞行器能否设计成功, 很大程度上取决于飞行器是否具备足够的抗失控能力.
高速飞行器耦合问题研究及抗失控能力设计一般建立在耦合动力学模型基础上, 通过耦合机理分析、 试验数据等总结出一系列适用于飞行器的典型操稳特性判据[7-13], 这些判据不仅可以在设计初期预测气动布局的好坏及其对操稳特性的影响, 帮助工程师改进气动布局以使飞行器获得最佳性能, 还可用来预测飞行器在当前气动布局下所需要的控制资源以帮助飞行器合理应对耦合的影响, 最后在设计完成后还可用此判据分析飞行器飞行过程中的稳定性以及控制策略的合理性.
本文在阐述高速飞行器面临的设计问题基础上, 回顾并整理围绕飞行器操稳能力形成的一系列设计判据, 总结发展规律, 为高速飞行器的设计提供应用指导.
1 高速飞行器设计面临的问题
1.1 静稳定裕度设计问题
传统的飞行器设计观念认为俯仰通道静稳定裕度在3%左右较好, 这样对气动特性和控制系统设计压力比较小, 然而纵向静稳定裕度的增大意味着牺牲了飞行器的最大过载和最大升阻比, 过高的静稳定性, 会牺牲飞行器的总体性能. 与此同时, 静稳定性的提高还需要能够产生更大纵向配平力矩的气动舵面操纵机构和更大功率的操纵舵机, 这给具有较大法向过载的高速飞行器设计带来严重的问题, 本就苛刻的载荷空间几乎很难承担舵机电池重量和体积的增加.
1.2 航向操纵设计问题
传统设计中, 飞行器的航向稳定和控制主要依靠方向舵实现, 控制系统对方向舵的操纵能力要求很高. 然而方向舵的效率随着Mach数和攻角的增加而下降, 因此在高Mach数和大攻角飞行条件下, 若满足传统设计方法对航向控制的要求, 高速飞行器方向舵和垂尾面积将非常巨大. 这将严重影响飞行器整体性能, 特别是阻碍设计上非常关心的升阻比的提高. 而且增大方向舵操纵面积会使得舵面铰链力矩巨大, 给伺服系统和舵机电源设计带来挑战.
1.3 三通道耦合问题
非轴对称布局的飞行器不同通道之间气动特性差异明显, 而且三通道气动力之间以及气动力与惯性力之间存在密切的耦合关联作用, 舵面的操纵效果也不是单独对某一个通道起作用, 因此传统的单通道解耦设计方法难以满足飞行器飞行包线内的控制性能要求.
1.4 设计安全边界问题
传统设计中, 将不同误差分布向单一最恶劣方向叠加, 以获得最安全的边界. 但是安全边界的过度扩大是以牺牲飞行器飞行性能为代价的, 对于性能要求很高的高速飞行器, 往往不能承受. 在不损害飞行安全的条件下, 合理分配误差分布, 对总体性能影响小的物理量的误差分布指标可以适当降低要求.
1.5 气动特性建模问题
高速飞行器的气动布局和气动特性日趋复杂,同时飞行器的高性能对气动特性的精度要求却在提高. 因此气动研究的工作量和难度越来越大, 需要采用更加先进的气动模型描述和管理方式. 在模型既能准确反映气动特性, 特别是耦合气动特性, 又能够降低气动数据规模前提下, 减小气动设计的工作量.
这些问题的出现并非一个偶然和孤立的事件, 发生的根源在于高速飞行器在飞行性能和机动性提高的同时, 飞行器的可操纵性下降. 随着飞行器性能的提高, 飞行器的操纵变得越来越困难, 飞行器偏离可控的弹道, 出现失稳或失控的危险性在增加.
由于抗失控性同飞行器的安全性密切相关, 从工程实现讲, 飞行器只有达到了一定的抗失控能力安全标准之后, 讲飞行器的性能才有意义. 抗失控性可以理解为飞行器设计上不能逾越的“红线”. 此外, 抗失控性除了同飞行安全性密切相关外, 还同飞行品质和飞行任务的完成质量密切相关.
在工程上, 提高飞行器抗失控性能, 可以有两种方法: 一种是牺牲飞行器的机动性, 降低飞行器性能指标以提高其抗失控能力. 这也是我们现有的设计中常采用的方法, 其好处是工程上易于实现, 如果在现有条件下需要进一步追求飞行器的高性能, 这种方法存在着几乎无法逾越的困难. 提高飞行器抗失控性能的第二种做法是, 提高对高速飞行器操稳特性的分析、 理解和预测水平, 设计既不牺牲飞行器的高机动性且具有高抗失控能力的飞行器. 显然第二种做法是一种更高明的做法, 但是要在工程上实现这一做法, 就需要我们提高对高速飞行器操稳特性的认识水平、 建立抗失控特性的分析手段, 发展飞行器操稳特性预测判据.
2 失控诱因
关于可能诱发飞行器偏离可控弹道, 出现失控危险的因素, Seltzer等[14]总结了几十年来失控领域的研究成果, 将导致可控飞行器失控的原因归结如下:
(1)飞行环境的不确定性. 由于高空飞行环境的复杂性, 基于地面试验和数值计算的高空飞行环境预测同真实高空飞行环境存在一定的偏差, 这种偏差在某些情况下, 会导致飞行器出现失控现象. 解决办法一方面是提高飞行器控制系统对复杂不确定环境的适应能力, 另一方面, 是提高对真实飞行环境的认识能力和预测水平, 前者是控制系统鲁棒性问题, 后者属于天地一致性问题.
(2)飞行器的大攻角气动特性. 飞行器大攻角飞行时, 在背部存在分离涡效应, 气动特性异常复杂, 会导致气动特性的非线性, 飞行器出现航向单一不稳定, 甚至横向和航线不稳定.
(3)交叉耦合控制. 表现在舵面操纵特性, 既有可能是副翼操纵时引起了不利的交叉偏航力矩, 也有可能是延迟或不正确的控制输入导致飞行器失控, 比较典型的如横航向静态耦合.
(4)惯性耦合. 飞行器在进行速度轴滚转时, 有可能会诱发不利的偏航和俯仰力矩, 使得飞行器易于失控.
(5)动力学耦合. 动力学耦合可能造成大攻角, 使飞行器易于发生失控, 典型现象是横航向动态耦合.
在大量飞行实践中, 人们逐步认识到对飞行器失稳特性影响比较大的耦合现象包括: 滚转惯性耦合、 横航向静态耦合、 横航向动态耦合和三通道耦合等.
从发现耦合现象到正确认识耦合现象, 再到利用耦合特性提高飞行器设计水平, 经历了一个漫长和曲折的过程. 这一认识是建立在昂贵和高风险的各类高速飞行试验基础之上[15-21](见表1), 来之不易. 这些由于耦合特性诱发高速飞行器失控的事故, 推动了人们对高速飞行器失控敏感性的重视和探索性研究, 并通过这些飞行实践逐步得到了如下共识: 牺牲飞行器性能来提高飞行器的抗失控能力, 并不能换来真正的飞行安全性, 终究是得不偿失的; 抗失控性能和机动性能同等重要, 在设计过程中需要同时考虑飞行器的失控敏感性, 以获得具有高抗失控能力的高速飞行器.
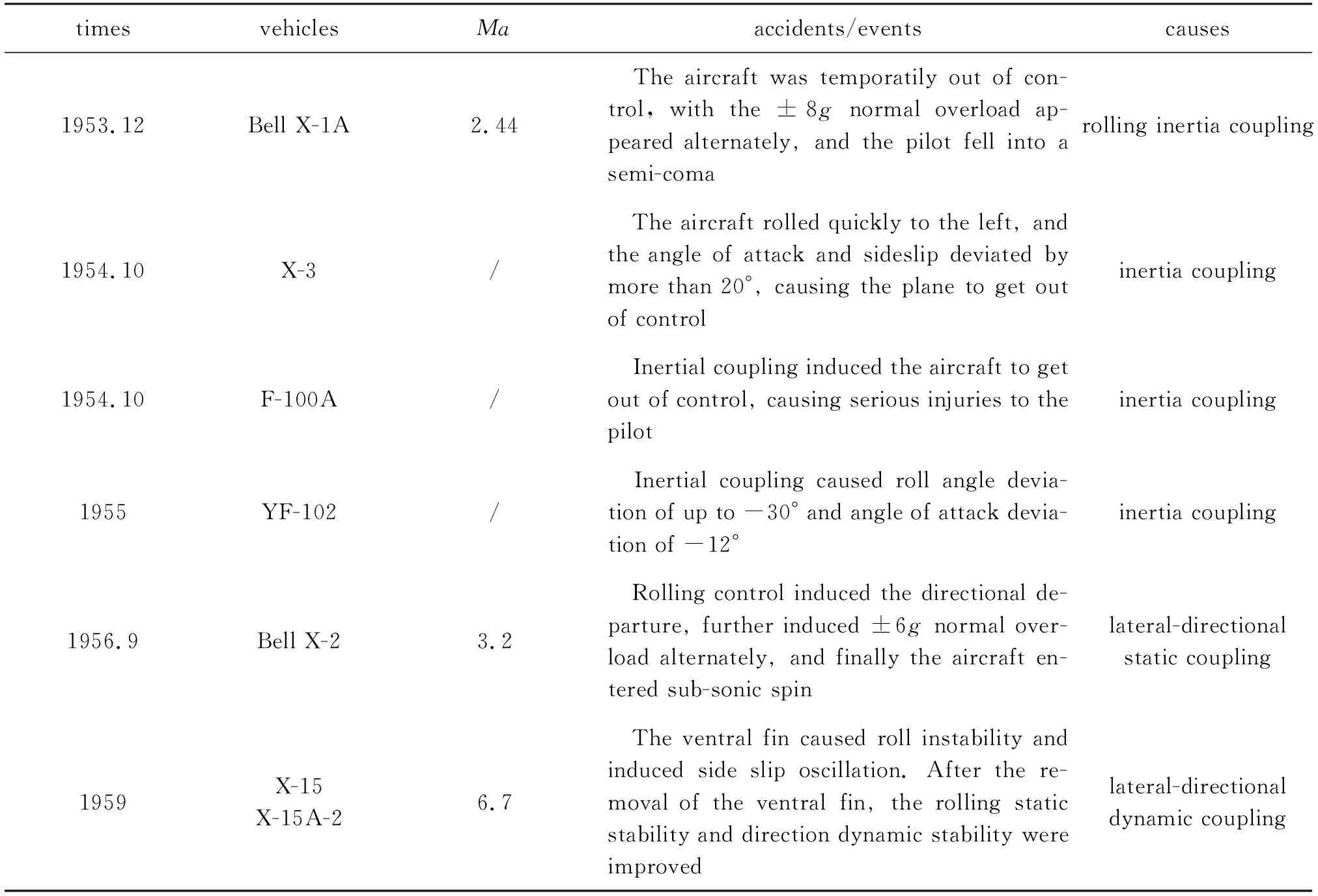
表1 耦合特性引发飞行事故一览表Table 1 List of flight accidents caused by the coupling characteristics
随后, 发达航天大国逐步摆脱了耦合特性对设计工作的束缚, 反而可以利用耦合效应来提高飞行器的性能, 发展了具有高抗失控特性的高性能高速飞行器设计方法, 总结出了一系列适用于飞行器设计的典型判据. 新设计方法进入到传统的“不稳定”设计禁区, 在这些设计区域内一样可以获得满足飞行性能要求的飞行器, 极大拓展了飞行包线, 为获得高性能的飞行器创造了条件.
3 常用判据
随着早期美国X系列研究机、 航天飞机、 天地往返运输系统等高速飞行器的不断研究发展, 发现了传统航向稳定性判据的不足, 进而促使了对横航向静稳定性判据的深入探讨, 产生新的横航向判断准则. 例如不对称操纵面偏转、 干扰力矩超过最大舵力矩、 负的气动阻尼力矩等. 为了预测高性能飞行器的横航操稳特性, 许多预测准则通过理论分析和飞行验证得到不断发展和完善.
3.1 横航向稳定性参数Cl β, Cn β判据
该判据用于判定飞行器的横/航向气动静稳定性, 为开环静稳定判据, 是最简单的偏离失控边界条件. 判据表达式如下:
Cn β>0: 航向气动静稳定.
Cl β<0: 横向静稳定(上反效应).
Cn β决定了荷兰滚模态的自然频率以及螺旋稳定性, 不适用过度的侧滑, 以及在大机动或存在湍流时的偏航运动.Cl β是影响荷兰滚阻尼和螺旋模态的主要因素, 是一个小负数时, 有比较好的荷兰滚阻尼, 是一个很大的负数时, 有稳定的螺旋稳定性.
Cl β与翼面位置、 滚转力矩系数、 空气弹性变形、 翼面和机身间的干扰有关, 而Cn β与机身和翼面有关. 该判据适用于受侧滑角扰动的静稳定的非增稳飞行器, 并没有考虑机动动力学和气动耦合的影响.
3.2 动态航向稳定性参数Cn β,dyn
该判据是飞行器失控敏感性最常用判据之一, 1958年由Moul等[7]提出, 是开环横/航向动稳定的必要条件, 也是荷兰滚稳定判据. 该判据在初步设计阶段非常有用, 判据表达式如下
Cn β,dyn>0
Cn β,dyn=Cn β(α,β)cosα-(IZ/IX)Cl β(α,β)sinα
Cn β,dyn不仅是航向气动稳定性Cn β的函数, 还是Cl β和转动惯量IX,IZ的函数.若航向不稳定即Cn β值为负, 此时如果横向稳定即(IZ/IX)Cl β为负, 也可使Cn β,dyn为正, 使飞行器荷兰滚模态稳定.
该判据主要用于初步设计阶段, 其影响主要体现在Cl β和Cn β上.Cn β,dyn判据是由线性的横/航向运动学方程导出, 在导出时略去了一些小量.在导出Cn β,dyn判据时, 若攻角较小,Cl β和Cn β与侧滑角呈线性关系, 当攻角稍大时,Cl β和Cn β与侧滑角呈非线性关系.该判据没有考虑机动动力学以及纵/横航向交叉耦合的影响.Cn β,dyn不能预测控制引起的偏离.通常计算Cn β,dyn时使用的静态数据和真实飞行数据并不一致, 从而影响了Cn β,dyn判据对真实飞行过程中偏离预测的准确性.
3.3 横/航向操纵偏离参数LCDP
该判据由Moul等[7]在1958年提出, 主要用来预测飞行器进行滚转操纵时, 诱导偏航力矩超过偏航静稳定力矩引起的偏航发散现象, 该判据是闭环操纵横航向静稳定必要条件.
判据表达式: 仅采用副翼进行横向操纵时, 称为副翼操纵偏离参数AADP
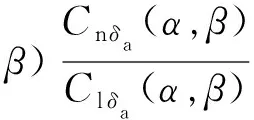
当AADP>0时, 飞行器能自动抵消侧滑的趋势, 使飞行器偏航方向稳定.
为减小运动学耦合导致的侧滑角较大现象, 常采用副翼-方向舵交联操纵, 其横向操纵偏离参数LCDP
LCDPCn β(α,β)-
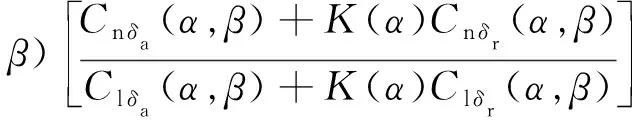
K(α)=Δδr/Δδa
当LCDP>0时, 横向操纵时飞行器偏航方向稳定.
从LCDP判据可知, 控制导致发散或偏离, 可能会出现滚转反逆状态(实际滚转方向与指令方向相反), LCDP是目前最基本的, 也是最广泛被人接受的闭环偏离敏感性判据.
3.4 Weissman组合偏离判据
1972年, Weissman[10]提出了一种由Cn β,dyn和LCDP组合而成的操稳判据, 称为Weissman判据. 最初是一个经验性的判据, 但与仿真和模拟飞行吻合得很好[22-23], 后经Titiriga等[24], Johnston等[25]不断改进, 最终形成了图1所示的判据平面, 现已成为现代飞行器设计的一个重要且实用的判据.

图1 改进后的Cn β,dyn和LCDP组合操稳特性判据平面Fig. 1 Plot of depature and spin susceptibility criteria
在区域A高增益时开环和闭环稳定. 在区域B, 存在滚转控制反逆, 随着增加驾驶仪或控制系统增益, 荷兰滚模态将会加剧而导致系统失稳. 在区域C和D静不稳定的弹体(Cn β,dyn<0)不能由滚转方向的控制稳定下来, 区域E和F显示静稳定的弹体可以通过滚转控制校正. 总的来说, 当LCDP为负时, 闭环滚转回路将导致振荡不稳定. 在采用副翼控制以及其他方式消除荷兰滚模态时, 必须采用过载或侧滑角反馈的方向舵辅助控制以增加航向的稳定性.
Weissman判据在一个判据平面上既提供了开环又提供了闭环横/航向稳定信息. 利用判据平面所预测的结果, 无论在偏离的类型, 还是在严重程度上, 与飞行试验数据都是一致的. 该判据操作性很强, 可以在飞行器设计的初始阶段很快计算出来, 以帮助确定飞行器的气动外形. 由于Cn β,dyn和LCDP判据推导过程中使用了线性解耦的纵-横/航向运动动力学方程, 并假定飞行器处于稳态飞行条件, 在推导过程中略去了高阶量, 因此会对Weissman图的判断精度产生影响.
3.5 β+ δ轴稳定性判据
1971年, Hodgkinson等[8]提出了由Cn β,dyn和LCDP组合成的另一种操稳判据, 用于预测飞行器失控状态下的临界攻角大小, 判据表达式为

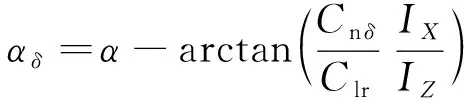
当α-β>0且α-β>αδ时, 飞行器稳定.
β轴方向定义为侧滑改变后引起的加速度的初始方向.δ轴方向定义为横向和横-航向输入后引起的加速度的初始方向.
该判据是Cn β,dyn和LCDP的变形,α-β>0也就是Cn β,dyn>0,α-β>αδ, 也就是LCDP > 0.
3.6 Johnston 1/Tθ3判据
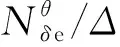
1/Tθ3判据由在A-7飞机非对称飞行时得出
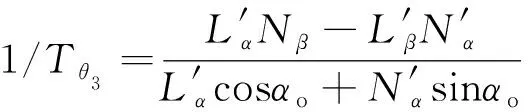
为了避免潜在的闭环螺旋发散, 1/Tθ3必须保持为正.
从设计和分析的观点看, 1/Tθ3参数指出纵-横/航向的气动耦合是导致飞行器失控的重要因素, 而从解耦的横/航向运动方程中导出的偏离参数/准则不能预测气动耦合的影响.
对于A-7飞机, 比较小的Cn β,dyn和LCDP值都可能导致A-7偏离, 但两个都不是主要因素. 而当Cn β,dyn和LCDP同为负值时, 会加剧纵-横/航向的气动耦合, 导致机头快速和剧烈的偏离.
1/Tθ3给出了由纵-横/航向耦合运动引起的闭环发散, 这是首个可以预测此类发散现象的参数. 1/Tθ3的导数表征了飞行器稳定性和在大攻角情况下侧滑角的重要影响. 另外, 在计算1/Tθ3时也估计了气动耦合和动导数对飞行器稳定性的影响.
3.7 Kalviste Mα,cop, Nβ,cop, K判据
该判据是由Kalviste[27]在1978年提出的, 考虑了非对称飞行(β≠0), 利用飞机纵-横/航向气动耦合和非线性的气动数据, 导出了预测飞行器稳定性的开环判据, 判据表达式为
Nβ,cop>0
Mα,cop>0
K<1
该判据表征了开环滚动静稳定性, 下标“cop”代表“coupled” , 表示该参数是由耦合运动学方程导出的, 因此可以用于非对称飞行情况.
非线性的耦合稳定性参数定义为
其中,
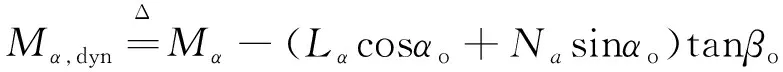
当得到非线性静态气动数据后, 可采用Kalviste稳定判据进行分析, 但分析过程需要绘制等高图. Kalviste使用等高线图(见图2)定义了3个失稳区域.

图2 Kalviste α-β静稳定图Fig. 2 Kalviste α-β static stability plot
(1)K< 0, 耦合振荡不稳定性.
(2)Mα,cop<0, 耦合的纵向发散(短周期在s平面的右半平面).
(3)Nβ,cop<0耦合的横/航向发散(荷兰滚根在s平面右半平面).
飞行器机动飞行时攻角和侧滑角的轨迹穿越不稳定区域表示飞行器有偏离趋势, 但这并不代表飞行器一定会发生偏离, 如果不稳定区域小, 飞行器偏离后可能进入稳定区, 如果不稳定区域大, 偏离会导致飞行器速率增加进而演变为临界旋转或螺旋运动.
Kalviste耦合的静稳定判据将开环、 对称、 静态的Cn β,dyn参数扩展为非对称飞行条件下使用, 其包含了大非线性气动数据和典型的大攻角飞行状态. 该判据是静态耦合的稳定判据, 并没有考虑潜在的由动不稳定引起的偏离以及由闭环控制造成的偏离.
3.8 Cn β-Cl β, 和Cn δa判据平面
该判据是由Bihrle等[28]在1978年提出的用于判定偏离敏感性和滚转反逆边界的准则. 该判据为经验性判据, 经过大量数据分析确定了判据边界, 可应用于判断大角度瞬态机动飞行. 在确定这个判据时做了如下假设:
(1)Cn β和Cl β的参数取自F-4, F-111, F-14和F-15等战斗机;
(2)比值IZ/IX是一个常值;
(3)边界只适用于纵向稳定的飞行器;
(4)对纵向控制不进行限制.
判据平面如图3所示.
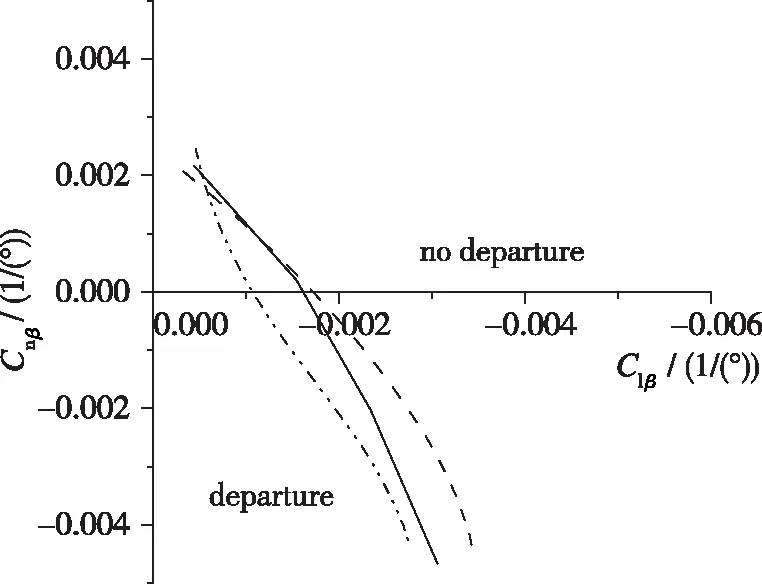
(a) Departrue boundary
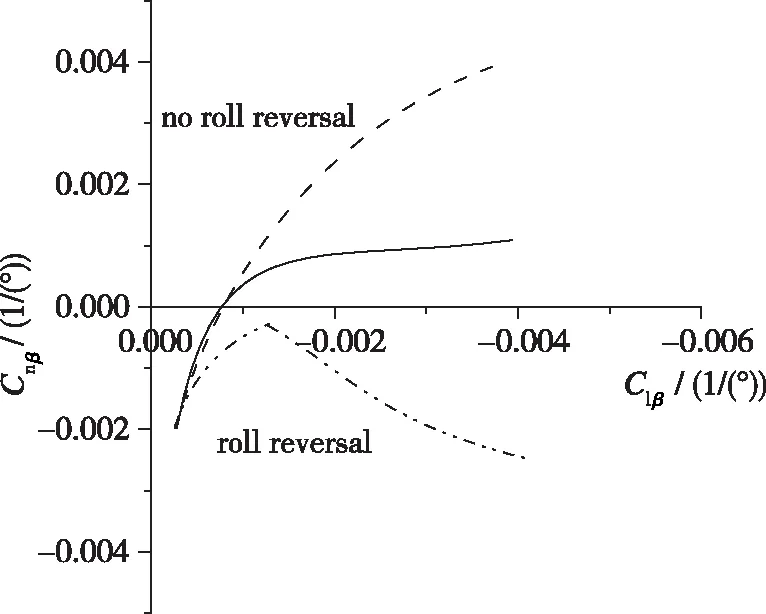
(b) Roll reversal boundary图3 Cn β-Cl β, 和Cn δa判据平面Fig. 3 Bihrle applied research design guidelines for departure susceptibility and roll reversal
对于设计抗偏离和滚转控制稳定的飞行器, Bihrle判据图在飞行器静稳定特性方面提供了与Weissman判据相似的信息. Bihrle判据图表征了小的正的上反效应(负的Cl β)可以通过增加航向稳定性的方式加以补偿. 另一方面, 航向静不稳定外形(负的Cn β)可以依靠横向稳定性抵抗偏离, 但是这种情况下会更容易出现滚转反逆.
Bihrle判据图既可用于飞机机动飞行, 判断其动稳定性, 也可用于考虑运动学耦合和惯性耦合以及非线性影响的情况. 需要注意的是Bihrle判据图是基于固定的惯量比(IZ/IX)和副翼力矩比(Cl δa/Cn δa), 而Weissman判据没有这样的限制.
3.9 Johnston 1/Tφ1>-0.5判据
该判据是由Johnston等[25]在1980年提出的, Johnston在闭环和对称飞行情况下, 提出了闭环的横-航向稳定判据, 用以判断滚转控制输入后是否会发生滚转反逆现象, 他把LCDP判据推广到了考虑增稳的飞行器上, 判据表达式为
1/Tφ1>-0.5 或ξφωnφ>-0.5
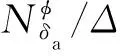
Johnston对4种不同外形的飞行器进行了研究, 分别研究了只存在开环动力学(也就是Cn β,dyn), 只存在闭环动力学(也就是LCDP, 1/Tφ1,ξφωnφ)以及同时存在开环和闭环动力学的影响. 试验结果如图4所示. 图中R代表抗偏离, S代表对偏离比较敏感, ES代表对偏离特别敏感. 可以看出抗偏离R和对偏离比较敏感S的分界线大致在-0.5.
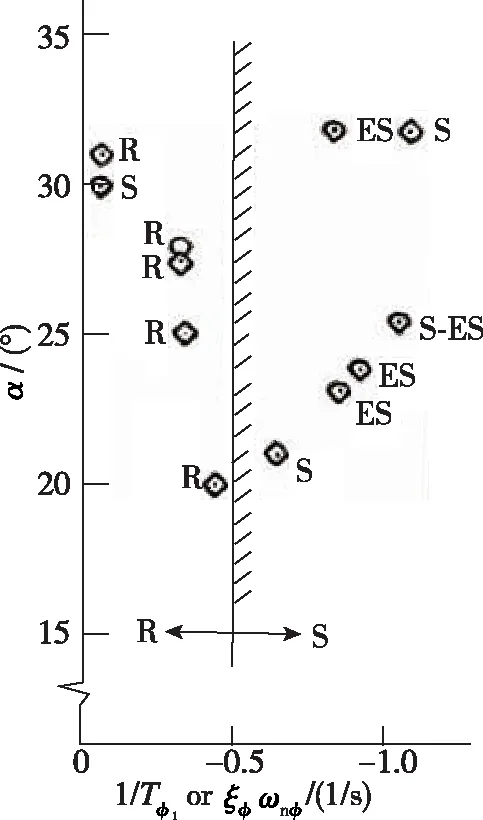
图4 偏离敏感等级随1/Tφ1或ξφωnφ变化趋势Fig. 4 Departure susceptibility rating versus lateral closed-loop divergence potential, 1/Tφ1 or ξφωnφ
如果在攻角和侧滑角所能达到的范围内, 通过对气动和飞控系统组合设计使1/Tφ1(或ξφωnφ)不小于-0.5, 则可预测飞行器没有滚转反逆现象. 1/Tφ1判据引入了飞控系统对偏离的影响, 可用来帮助设计抗偏离的飞控系统. 这对新型高速飞行器(无垂尾, 隐身)尤为重要, 因为这类飞行器开环航向稳定性非常低, 必须依靠飞控系统进行增稳. 这个判据对飞行器的开环稳定性没有限制.
与闭环偏离判据LCDP不同, 1/Tφ1判据没有对3自由度的横/航向运动方程做任何假设, 因此可应用在考虑飞控系统的6自由度弹体动力学模型中. 该判据是使用单一的非线性模型通过仿真结果得到的, 判据可能与气动外形相关, 其普适性需要进一步验证.
3.10 闭环横向偏离参数Cn β,app
该判据是由Pelikan[29]在1983年提出的, 是在开环特性基础上发展起来的闭环操稳特性判据, 用闭环横向偏离参数Cn β,app来表示, 将Cn β,dyn判据拓展到考虑控制的影响, 判据表达式为
Cn β,app>0
其中,
该判据用来评价不同的输入(中性控制、 横向保持、 协调控制、 交叉控制和单独方向舵)对弹体横/航向静稳定性的影响.
Cn β,app判据包含了侧滑角引起的气动非线性特性以及不同控制输入的影响, 在初步设计飞行控制律抑制偏离时非常有用.
Cn β,app判据没有指出由于不稳定动力学(气动耦合, 惯性耦合)带来的偏离趋势, 也没指出由驾驶仪闭环控制造成的偏离趋势类型, 再者, 这个参数只考虑了横/航向轴的偏离, 未考虑任何纵轴或纵-横/航向耦合可能导致的偏离.
3.11 Kalviste动稳定参数
1989年Kalviste等[30]基于飞行器的非线性气动数据, 分析了转动运动中动能和势能与静稳定性的关系, 得到了开环纵-横/航向动稳定参数, 可应用于评估飞行器存在大耦合动力学状态时的开环稳定性, 判据表达式为
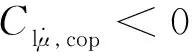
如果不满足上述稳定方程条件, 则可判断飞行器处于局部不稳定区, 这会使飞行品质下降, 比如不可预测的控制响应等, 但局部的不稳定不能表征飞行器在加入控制后会失稳.
这5个参数可以画在α-β平面上, 用来确定是否有不稳定区域存在, 如图5所示.
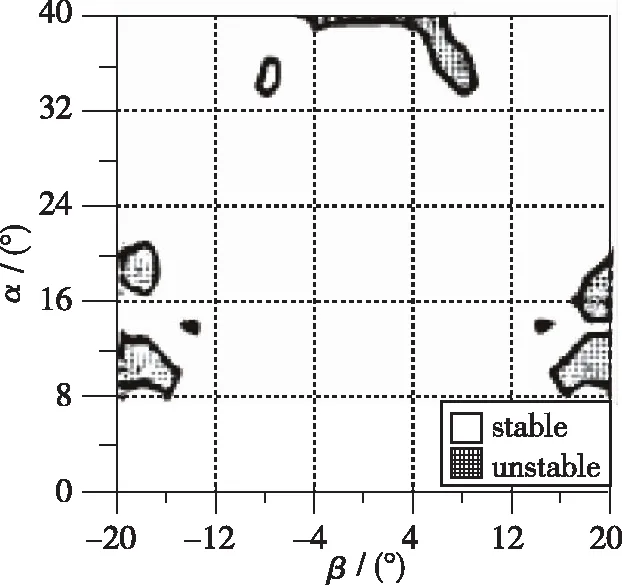
(a) Cn β,cop
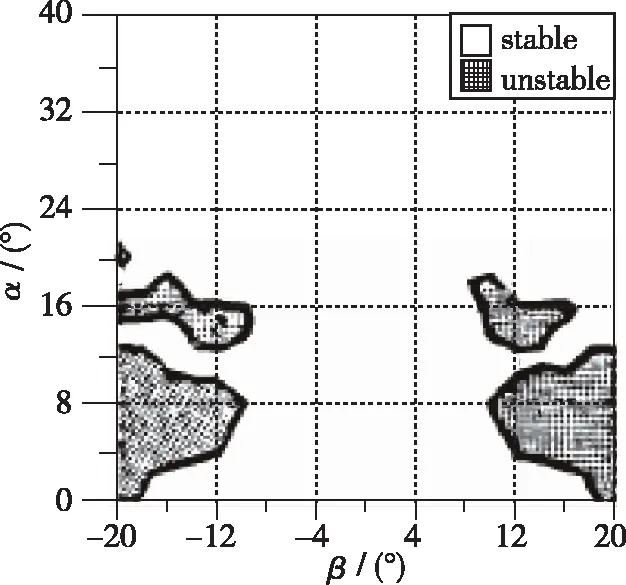
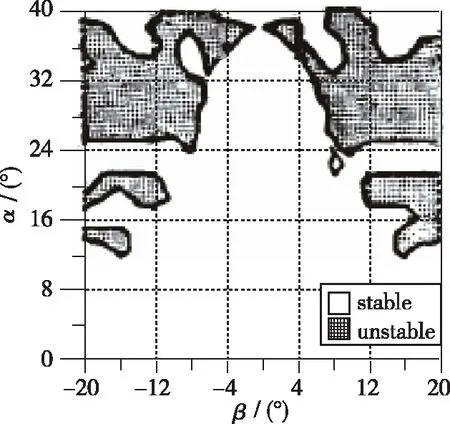
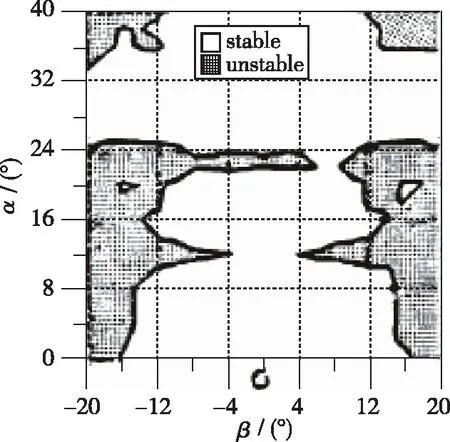
(d) Cmα,cop
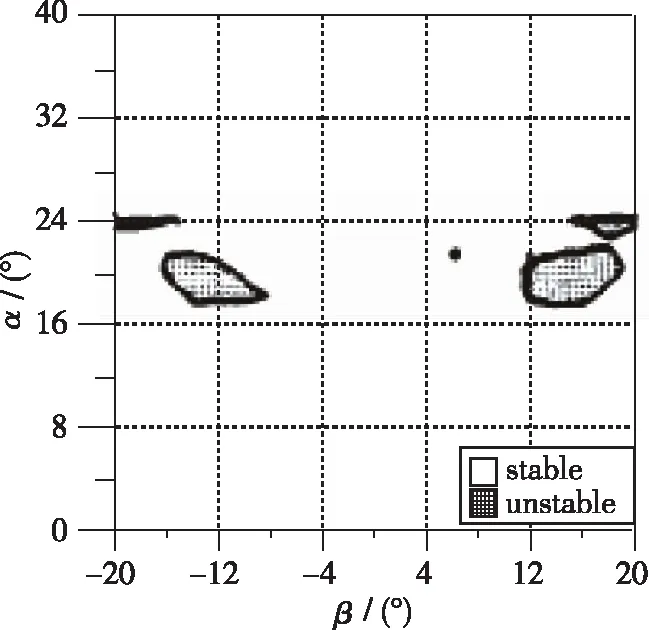
图5 Kalviste稳定参数对攻角和侧滑角的稳定域图Fig. 5 Kalviste stability parameters versus angle-of-attack and sideslip angle
Kalviste建立的运动学方程没有考虑弹道稳定性的影响(气动力、 推力和重力造成的瞬态模式), 这排除了可能的“快”模式和“慢”的轨迹模式(包括常规的螺旋和姿态稳定模态)的耦合影响. Kalviste认为在引入轨迹影响后, 由这个判据预测的气动稳定特性可能会发生变化.
3.12 横向稳定性特征参数LSDP
耦合作用下横航向运动具有两种稳定性主导模式: 横向主导和航向主导. 其中航向主导模式是偏航轴气动角β导致的同轴偏航力矩为主导稳定性参数, 更加接近单轴弱耦合运动特征; 而横向主导模式则是偏航轴气动角β导致的滚转力矩为主导稳定性参数, 呈现了交叉轴耦合运动特征. 这表明侧滑角导致的两轴稳定性导数相互关系是重要耦合特征参数.
航向动稳定性可以分为航向主导和横向主导及二者相当3种情况. 为了表示横航向稳定性之间的关系, 引入横向稳定性特征参数LSDP(lateral-directional stability dominant parameter).
当横向稳定性占据主导地位时, LSDP值趋近于1; 航向稳定性占据主导地位时, LSDP值趋近于0; 当LSDP值小于零时, 表示航向动稳定性参数Nβ,dyn小于零. LSDP的不同取值范围表征了不同的稳定性特征.
3.13 横航向闭环控制策略选择判据
闭环控制策略选择判据: 在动态航向稳定性参数稳定(Cn β, dyn>0)的前提下, 按照飞行器参数在kari-1/CP判据平面中的落区, 选择对应控制策略. 其中kari为副翼方向舵交联参数, 1/CP为操作耦合参数的倒数.
副翼方向舵交联参数体现了横航向两个轴向操纵舵面对稳定轴系下偏航力矩的操纵比, 表明了两个舵面抑制或者诱导侧滑角的能力.
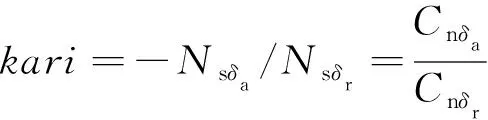
操纵耦合参数倒数1/CP, 即稳定轴系下的滚摆比与副翼操纵滚转与偏航力矩的操纵比的比值, 或者说是滚摆比对于操纵比进行了归一化处理, 体现了滚摆比这一敏感反馈参数的影响.
在控制策略选择判据平面中, 当1/CP<0时, 为有利耦合区, 当0<1/CP<1时, 为抑制耦合区, 当1/CP>1时, 为利用耦合区, 当kari较大时, 为控制困难区.
耦合作用下闭环控制策略选择判据, 能够选择灵敏度高的反馈通道, 有效利用侧滑角产生机动力矩的力学机制, 降低舵偏需求, 根据判据特征参数落区选择有效横航向控制策略.
4 常用判据总结
从判据的发展过程可知, 判据是从简单到复杂, 从开环到闭环, 从静稳定到动稳定, 从对称飞行到不对称飞行, 从不考虑耦合的影响到考虑耦合因素的影响, 从不考虑高阶量到考虑高阶量而逐步发展完备, 但是从辩证法可知, 事物都有两面性, 简单的判据直观易行, 但预测准确性受到限制, 而复杂的判据可能适用于复杂情况, 但使用变得复杂. 而且各个判据都有其假设的应用条件及优缺点, 因此在利用判据时应该考虑其假设和优缺点, 选择合适的判据加以应用. 表2给出了各个判据的应用条件.
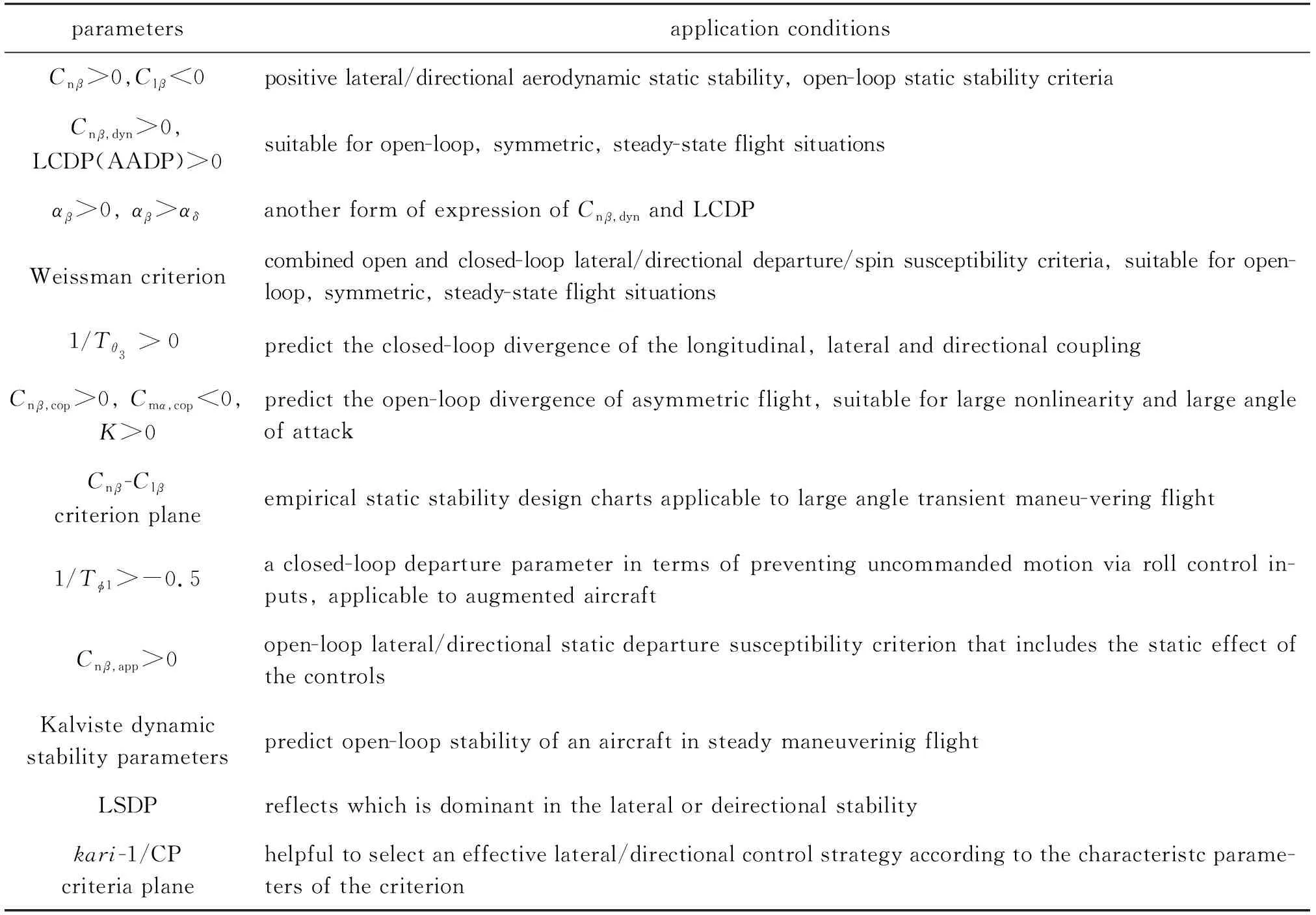
表2 判据的适用条件Table 2 Application of the criteria
目前在设计新型飞行器时, 通常会选择上述几种判据的组合进行操稳特性预测, 如Cn β>0,Cl β<0判据,Cn β,dyn>0和LCDP(AADP)>0判据,Cn β,app判据以及Weissman判据.
5 判据的应用
判据的提出是为了更好地指导设计, 将预测判据应用于现代高速飞行器的设计, 更进一步分析了先进飞行器设计中的准则和方法, 也有助于加深理解预测判据的重要价值和应用前景.
美X-33验证飞行器、 高速飞行试验飞行器(HYFLEX)和日本的高机动试验飞行器(HIMES)等[31-34]的设计都广泛引入并应用了各类判据. 其中, X-33的设计过程中使用横航向稳定性参数Cl β,Cn β,Cn β,dyn, LCDP和Weissman等判据进行设计; 在HYFLEX的设计过程中使用参数Cl β,Cn β进行静稳定分析, 然后得出偏航喷管主要用作滚转控制, 而副翼主要用作侧滑控制的规律, 这种对执行机构的使用与航天飞机类似. 日本在HIMES的设计过程中为验证高速再入时的纵向和横侧向动力学特性, 采用了Cn β,dyn, LCDP来验证其气动特性, 并判定飞行器的操纵面的操纵性能.
国内围绕飞行器设计判据也开展了相应的应用研究工作. 陈功等[35]针对升力式再入飞行器的气动特性和控制方式,分析了将传统Weissman判据推广应用到升力式再入飞行器设计中面临的一些主要问题. 仿真分析表明,升力式再入飞行器对应的Weissman图与传统航空飞行器存在明显不同,可以将其推广应用到升力式再入飞行器设计中. 蔡硕[36]引入横航向稳定性判据分析了无垂尾飞行器横航向稳定性. 曹玉腾等[37]推导建立了大攻角、 大侧滑角条件的飞行器动态偏离判据和操纵偏离判据,并对某再入飞行器应用新偏离稳定判据,进行了偏离稳定性分析.
6 结论
利用耦合机理和抗失控判据研究成果, 在短期内能够以较小的代价解决高速飞行器在气动布局和控制方面的设计难点, 从而优化飞行器性能, 加快飞行器性能升级; 从长远看可为高性能飞行器的研究设计提供坚实的理论基础和良好的技术支撑, 从而在先进飞行器的研究过程中少走弯路. 综上所述, 我们有必要发展利用耦合特性进行高速飞行器设计的新方法和新判据, 以进一步提升飞行器的抗失控性能.
