基于SPH方法的高速列车风阻制动板制动力研究
2021-12-13张硕果胡湘渝米彩盈
张硕果, 胡湘渝, 米彩盈
(1. 西南交通大学机械工程学院, 四川成都 610031; 2. 德国慕尼黑工业大学机械工程学院, 巴伐利亚州加兴市 85747)
引 言
我国高速列车运行速度已提高至350 km/h[1],提高速度的同时, 让列车在规定的制动距离内减速停车, 是目前时速300 km/h以上列车面临的一个重要问题. 尤其在紧急制动时, 列车必须在与最高速度对应的制动距离内及时转移掉巨大的动能. 由于制动力不能超过轮轨间的黏着力, 且黏着系数随车速的增加而下降, 因此传统黏着制动方式已难以满足制动要求, 有必要研究非黏制动方式作为黏着制动方式的补充[2].
时速300 km/h以上的高速列车通常采用轨道涡流制动、 磁轨制动和风阻制动3种非黏制动方式; 欧洲国家采用的磁轨制动和轨道涡流制动均安装在转向架上, 从而导致簧下质量增加, 且会产生磁辐射和轨道磨损等各种影响; 日本采用的风阻制动则是在车顶安装利用空气阻力的风阻制动装置[3].
随着列车运行速度的增加, 空气阻力与速度平方成正比, 列车速度达到300 km/h以上时, 空气阻力占总阻力的80%左右, 因此风阻制动方式作为黏着制动方式的补充在高速段更具优势[4]. 装备风阻制动装置的MLU002N磁悬浮列车和“姊妹”高速列车(Fastech 360S型和Fastech 360Z型)均通过了时速400 km/h条件下的风阻制动板性能测试; 时速360 km/h条件下采用风阻制动方式的Fastech 360S型列车, 其制动距离与其在时速275 km/h条件下不采用风阻制动方式的制动距离近乎相等; 通过“姊妹”高速列车对风阻制动装置的机械结构和制动性能进行了大量测试[5-7]. 各种测试结果充分表明风阻制动装置在紧急制动时具有良好的可靠性和较高的应用价值[8].
高見創等[9]通过大型风洞实验对风阻制动装置实物样机进行性能测试, 给出了动作特性和阻力特性等实验结果. 吉村等[10]在以往各种风洞实验基础上, 设计制造出风阻制动装置, 在宫崎实验线上进行了实车实验. 苗秀娟等[4]采用大型流场数值计算软件CFX5.3进行数值模拟研究, 论证了高速列车安装制动板能获得较大的风阻制动力, 并说明了带折角的制动板比不带折角的制动板能产生更好的增阻效果. 高立强等[3,11-12]采用流体仿真软件FLUENT首先对制动板在不同的固定开启角度条件下进行静态载荷分析, 验证了制动板的机构性能和设计方案; 其次对不同几何外形的制动板进行对比分析, 得到了相对性能最好的板型; 最后研究了第1排制动板高度和横向间距变化对后排制动板的干扰规律, 并通过风洞实验验证了数值模拟的可靠性和计算精度. 田春等[1]采用流体仿真软件FLUENT对比分析了不同布置方案中, 沿纵向位置各制动板的制动力规律和周围流场特性. Zuo等[8]通过数值模拟和风洞实验对设计开发的风阻制动装置样机进行了验证测试, 对风阻制动板在不同固定开启角度和车速条件下的气动特性规律进行了较系统的研究, 并分析了制动板响应时间和可提供的最大制动力.
风阻制动装置的研究须通过风洞实验和数值模拟进行相互验证. 通过风洞实验可以获取更完整可靠的数据, 尤其是制动板开启过程中的相关数据, 如制动板运动规律、 制动力变化规律等, 目前该类数据主要依靠风洞实验获取. 由于实验周期、 成本和实验设备等因素的限制, 难以通过风洞实验对风阻制动装置进行多次验证和改进, 相比之下, 数值模拟在制动板研究中具有很大优势. 基于传统网格划分的数值模拟方法较难实现对制动板制动过程的动态模拟, 其研究范围存在一定局限. 尤其在选取制动板最佳开启角度的研究中, 由于模型修改的难度及工作量增大导致数据样本量受限, 相关数值模拟研究主要通过选取少量固定开启角度进行仿真, 与风洞实验数据进行近似验证.
光滑粒子流体动力学方法的应用, 在一定程度上解决了流固耦合数值模拟中自由表面、 变形界面、 运动交界面以及极大变形问题[13]. 通过SPH方法能够较容易地实现不同最大开启角度条件下风阻制动装置开启过程的动态数值模拟.
1 数值方法
1.1 空气动力学方程

(1)
式中, p为空气压力;τ为黏性切应力.
定义无量纲空气阻力系数Cd, 则由式(1)可得到风阻制动板制动力的一般表达式
式中,ρ为空气密度(单位: kg/m3),v为列车运行速度(单位: m/s),A为制动板沿列车运行方向投影面积(单位: m2).
1.2 流体控制方程
列车车速为300 km/h,Ma=0.245<0.3, 流体视为不可压缩流体[11]; 制动板的整个制动过程在湍流边界层内完成. Lagrange形式的不可压缩流体控制方程为:
质量守恒方程
(2)
动量守恒方程
(3)
式中,t,ν和g分别为时间、 运动黏度和重力加速度.
制动过程中制动板位置突变导致流场密度分布不均匀, 因此采用弱可压缩SPH方法模拟不可压缩流体[15-16], 压力p可通过密度ρ表达为
(4)
式中,ρ0为初始密度;C0为人工声速.
为控制流体密度变化率在1%左右, 最大Mach数应小于0.1[17]. 数值模拟中Ma=v/C0, 取C0=10v.
1.3 SPH流体控制方程
SPH方法运用插值核函数并借助一组无序点上的值将任一宏观变量表示成积分插值进行计算, 则任意连续函数A(r)可近似表达为

式中,W(r-r′,h)为核函数;h为定义核函数影响区域的光滑长度;r,r′为粒子坐标位置.
基于SPH方法的二维数值模拟中, 在将式(2)和式(3)转化为支持域内所有粒子叠加求和的离散形式时, 用下标a,b表示流体粒子, 下标i,j表示固体粒子.
质量守恒(2)可通过流体粒子a所在位置处密度的核函数估计表达, 该表达式利用粒子a支持域内流体粒子和固体粒子同时进行求解计算, 解决了两种粒子密度不同导致的流固交界面密度不连续的问题[18]
式中,ρa,ma分别为密度, 质量;Wab为核函数W(|rab|,h),rab=ra-rb.
在不考虑重力作用的情况下, 动量守恒方程(3)可转换为[18]
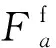
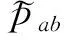
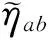
固壁边界采用虚粒子方法, 将固壁离散成一排或几排虚粒子, 代表固壁参与SPH插值运算, 模拟流固交界面处固体粒子与流体粒子的相互作用, 对于一对相互作用的虚粒子和流体粒子, 可以近似为[20]
(5)
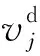
(6)
利用式(5)将式(6)简化为
1.4 刚体控制方程
假设风阻制动板为刚体模型, 且不考虑重力, 采用与固壁边界相同的固体粒子, 受到流体压差阻力和黏性力的共同作用. 制动板的运动分为刚体质心的平面移动和绕刚体质心的转动[21]:
刚体质心平面运动方程为
(7)
式中,M为刚体质量,v为刚体质心速度,fi为固体粒子所受流体压差阻力和黏性力.
刚体绕质心转动的转矩方程为
(8)
式中,I为惯性矩,R为刚体质心位移矢量,Ri为固体粒子位移矢量,ω为角速度.
由式(7)和式(8)得到单位质量固体粒子的位移方程
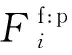
(9)
(10)
制动板所受合力F为
合力F沿x轴正向分力即为制动力Fx

1.5 时间积分
SPH方法的时间积分方式采用蛙跳算法[16,22], 在交错的时间点计算粒子位置和速度, 每经过半个时间步长, 速度v进行一次更新; 每经过整数个时间步长, 粒子密度ρ和位置r进行一次更新, 计算过程为
一个时间步长结束时, 速度v最终更新为
为保证数值稳定性, 应同时满足以下条件:
CFL条件
式中, |U|为速度绝对值的最大值.
黏性条件
2 风阻制动板模型
2.1 风阻制动板板型
迎风面积相等的各种板型制动板中, 凸形板和车顶随形板所提供的制动力稍小于平板所提供的制动力, 凹板形所提供的制动力稍大于平板所提供的制动力, 且整体而言, 各种板型制动板所提供制动阻力的变化幅值均较小[3]. 相对于不带折角的风阻制动板, 带折角的风阻制动板对气流具有阻滞作用, 其增阻效果更好[4]. 因此选择便于制造的边缘为直角的矩形平板, 见图1.
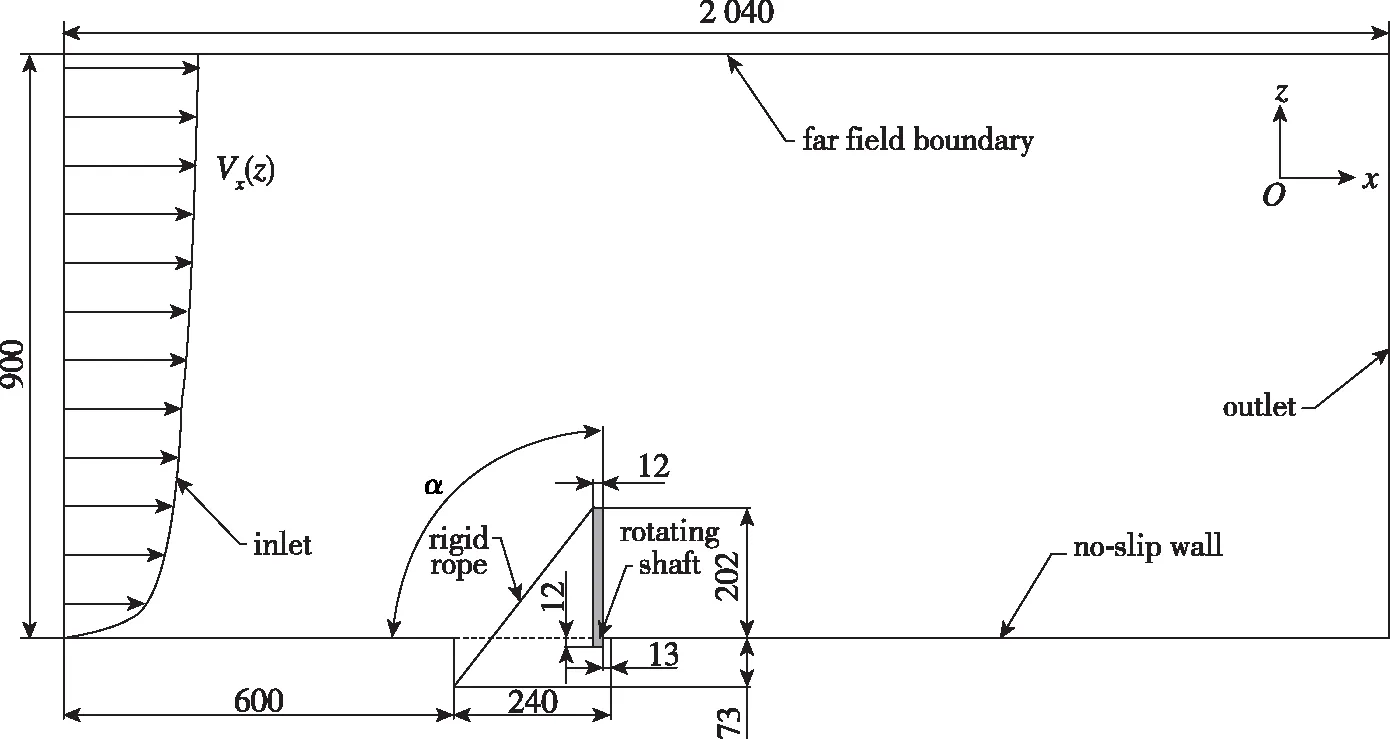
图1 计算域示意图Fig. 1 Computational domain
2.2 车体模型
高速列车整车风阻制动装置的布置存在多种方案, 不同布置方案下, 整车气动特性不同, 且不同位置的风阻制动板气动特性也不同. 气流在流经高速列车流线型车头时, 在距车头前端约10 m内达到临界Reynolds数, 层流转捩为湍流, 并沿列车表面延伸. 若忽略车顶弓网等凹凸形状电气设备的影响, 则车顶在宏观上可近似为平滑表面. 在沿流线型车头流向的初始条件和压力梯度影响下, 湍流边界层厚度δ从车头前端处起, 快速增厚至车体宽度的1/3, 此后受二维气流和三维气流的影响, 边界层厚度缓慢延伸至中间车附近达到最大值, 大约为1 m[5].
由于主要对风阻制动板运动规律和制动力变化规律进行研究, 因此以中间车的平面车顶作为车体模型对单个风阻制动板装置进行仿真分析, 简化忽略列车车体、 曲线轮廓及弓网等电气设备的影响, 见图1.
2.3 风阻制动板尺寸
制动板背风面在制动板长宽比较小(L/W<1)的情况下会产生与交替状涡激振动有关的非对称Kárman涡街[9], 因而L/W应尽量大于1.
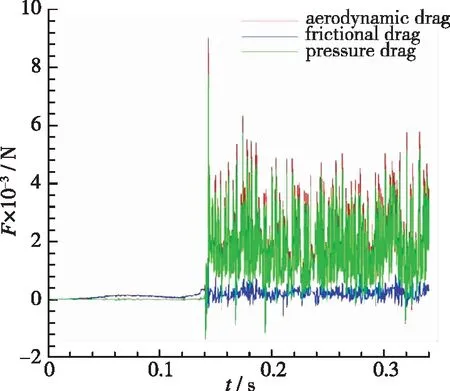
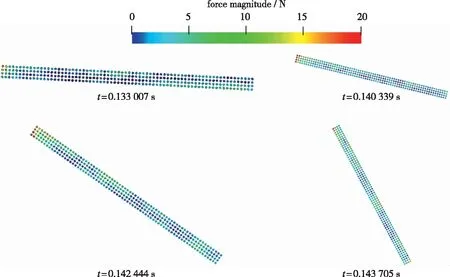
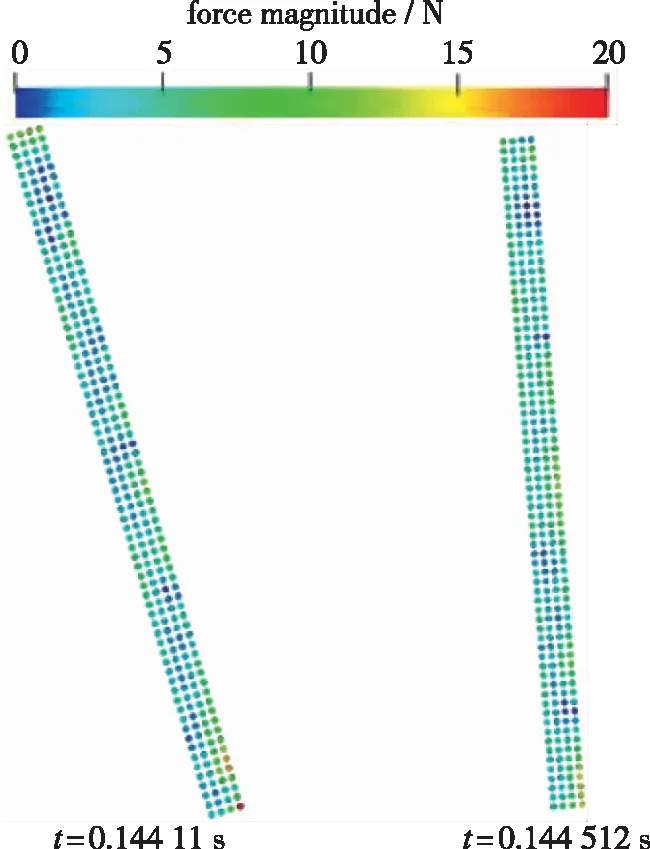
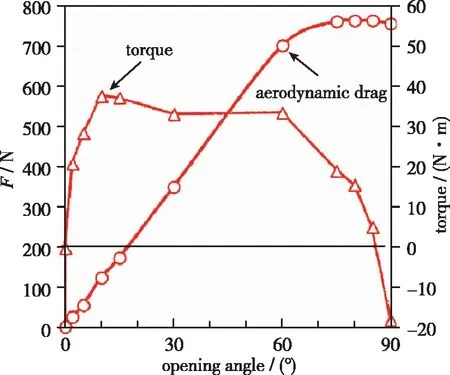
由摩擦速度和制动板长宽比计算得到湍流边界层内垂直制动板的阻力系数, 再分析得到阻力系数随制动板高度(即宽度W)与边界层厚度之比W/δ变化的规律, 其近似为关于W/δ的指数函数关系[9]. 当W/δ<1时, 阻力系数与W/δ正相关; 当W/δ>1时, 阻力系数变化不大. 在考虑边界层厚度、 列车车顶宽度及电网高度等因素的前提下,W的最佳设定范围为0.2 在满足L/W>1和0.2 风阻制动装置为箱体形状, 装置内有转轴、 液压杆等机械结构, 由于其形状尺寸对流场影响较小, 因此忽略该类机械结构, 将其简化为仅考虑制动板和凹形箱体的结构, 见图1. 二维数值模拟中, 在制动板上安装铰链模拟其转动; 制动板与箱体之间安装刚度足够大的刚性绳, 避免产生拉伸, 模拟制动板开启至最大角度时液压杆的约束作用; 通过改变刚性绳长度对最大开启角度α进行设置, 如图1. 湍流边界层流场中,Re=2.46×107, 空气初始密度ρ0=1.29 kg/m3, 以制动板宽W=0.214 m 为特征长度,则流体初始动力黏度μ为 流场入口速度分布用一般幂乘公式表示[9] (11) 式中,δ为边界层厚度,δ=1 m;n为幂指数,n=9~11, 取n=10;U0为自由流流速,U0=83.3 m/s;v(z)为距车体表面高度z处平均流速;z为距车体表面高度. 流场采用平滑加速至稳定流速的方式[21], 速度控制方程为 (12) 式中,t为物理时间;T为加速时间,T=0.1 s. 列车车顶边界层厚度近似1 m, 在保证计算精度的前提下, 为降低计算量, 将二维数值模拟中的计算域高度减小为0.9 m. 如图1所示, 计算域上边界采用远场条件, 固壁粒子速度vj应与湍流边界层中对应位置的流速相同[23], 由式(11)计算得vj=vx(0.9)≈82.43 m/s; 考虑风阻制动装置箱体形状对流场的影响, 计算域下边界采用凹形形状模拟车顶表面, 制动板表面和下边界为无滑移壁面边界条件, 其固体粒子速度vj均为0. 流体粒子从入口边界进入流场, 在出口边界流出后再次回到入口边界进入流场, 为避免能量耗散导致流速降低, 流体粒子在入口边界处经缓冲加速器再次加速后进入流场, 流场流速稳定在列车运行速度, 同时计算域长度不宜过长, 为2.04 m. 考虑制动板背风面流场的充分发展, 制动板位于前端约1/3处. 在列车时速为300 km/h, 风阻制动板最大开启角度α=90°的条件下, 以风阻制动板的制动过程为研究对象, 进行时长t=0.34 s的动态模拟, 大致分为5个阶段对流场变化和制动板受力变化进行分析, 得到制动板运动规律、 受力分布和制动力变化规律, 并计算不同α条件下制动板所提供制动力Fx, 得出Fx随α变化的规律, 给出了风阻制动板产生最大制动力的适宜开启角度. 图2和图3分别给出了风阻制动板在制动过程中所提供气动阻力和升力的变化规律, 其中气动阻力的变化规律与图4中高見創等[9]通过大型风洞实验所得的气动阻力规律大体一致. 高見創等[9]选用边缘为直角的矩形平板作为风阻制动板, 其宽度和高度分别为0.500 m和0.210 m, 因此图4中风阻制动板平均气动阻力值约为图2中风阻制动板平均气动阻力值的一半. 风洞实验中制动板响应时间(0.06 s)与SPH数值模拟中制动板的响应时间(0.025 s)较接近, 验证了风阻制动板满足紧急制动的快速响应要求. 图2 气动阻力Fig. 2 Aerodynamic drag 图3 升力Fig. 3 Lift 图4 阻力板动作特性—响应时间[9]Fig. 4 Performance characteristic—response time[9] 大致将制动过程分为以下5个阶段对流场细节和制动板受力变化进行分析: 阶段1: 0 流体黏性很小, 沿x轴正向黏性力为较小正值, 沿z轴方向黏性力为0. 制动板沿x轴方向投影面积为制动板厚度横截面, 因而沿x轴正向压差阻力几乎为0. 制动板与箱体边缘存在间隙, 见图1, 箱体内部与外部流场连通, 少量流体从前端缝隙流入, 后端缝隙流出. 因此气动阻力较小且主要由黏性力组成, 见图2; 升力主要受压差阻力影响, 在0附近微小波动, 见图3. 阶段2:t=0.12 s.为保证制动板顺利开启, 制动板以匀角速度(140 rad/s)运动0.000 5 s, 主动开启4°(打开角度5°以下[9]),模拟液压杆伸长推动作用. 由于时间步长原因, 数值模拟中制动板开启时刻(t=0.119 927 s)与SPH程序所设置的开启时刻(t=0.12 s)有细微差别, 可忽略不计. 如图8和9(b)所示, 制动板速度突变, 进而制动板位置也发生突变, 导致流体密度变化, 见图7 (b)和(c). 图7(b)中, 制动板上方区域流体密度大于其下方, 由式(4),(9)和(10)可知, 流体密度增大, 支持域内粒子数量增多, 制动板上表面受到的压力和黏性力大于其下表面,如图6(b); 图7(c)中, 制动板下方区域流体密度大于其上方; 制动板下表面受到的压力和黏性力大于其上表面, 如图6(c). (a) t=0.119 524 s (b) t=0.119 927 s (c) t=0.120 331 s (d) t=0.139 741 s (e) t=0.141 8 s (f) t=0.142 607 s (g) t=0.319 291 s (a) t=0.119 524 s (b) t=0.119 927 s (c) t=0.120 331 s (d) t=0.142 607 s图6 流场相对压力Fig. 6 Relative pressure nephogram (a) t=0.119 524 s (b) t=0.119 927 s (c) t=0.120 331 s (d) t=0.142 607 s图7 流体密度分布云图Fig. 7 Density nephogram 图8 风阻制动板角速度Fig. 8 Angular velocity of the aerodynamic brake panel (a) t=0.119 524 s (b) t=0.119 927 s (c) t=0.142 607 s (d) t=0.143 415 s图9 风阻制动板速度云图Fig. 9 Velocity nephogram of the aerodynamic brake panel 沿x轴正方向, 黏性力无较大波动, 流速如图5(b)和(c)所示, 无明显梯度变化, 同时压差阻力作用面为面积很小的制动板厚度横截面, 因此压差阻力近似为0, 气动阻力无显著变化, 见图2. 流体密度变化主要发生在制动板上下区域, 沿z轴方向黏性力的变化可忽略, 升力的瞬时较大波动主要来自压差阻力, 见图3. 阶段3: 0.12 s 对比分析图5(d)和(e), 背风面和迎风面区域流速逐渐增大, 且背风面初始流速比迎风面大, 同时考虑速度边界层分布的影响, 沿x轴正方向流速梯度变化和沿z轴方向制动板投影面积逐渐减小, 沿z轴方向流体速度差和沿x轴方向制动板投影面积逐渐增大. 因此制动板气体阻力逐渐增大, 升力稳定在0附近, 见图2和3. 制动板在气动阻力的主要作用下加速开启, 如图8所示, 制动板角速度增长速率逐渐增大. 阶段4:t≈0.145 s. 制动板运动至垂直车顶位置时, 受刚性绳约束, 制动板运动速度骤降, 如图8, 9(c)和(d)所示, 流场产生剧烈瞬时波动, 见图5(f), 制动板迎风面与背风面之间、 上下方之间均产生较大压差, 见图6(d). 图7(d)中, 制动板周围流体密度分布不均匀, 迎风面和下方区域流体密度增大, 背风面和上方区域流体密度整体无明显变化. 沿x轴正方向, 黏性力出现较小增幅, 压差阻力作用面积达到最大, 压差阻力达到瞬时最大值, 见图2; 沿z轴方向, 黏性力产生很大波动并达到最大值, 压差阻力作用面为较小的制动板厚度横截面, 因而增幅较小, 见图3. 因此, 制动板气动阻力和升力均出现很大的瞬时波动并达到最大值. 阶段5: 0.145 s 图2和图3中制动板气动阻力和升力迅速降低并收敛至平稳波动. 如图10(b)和(c)所示, 制动板背风面区域不断产生旋涡, 箱体内部持续存在一个旋涡, 且由图5(g)可知, 箱体内部旋涡速度逐渐降低至稳定状态. (a) t=0.139 741 s (b) t=0.161 263 s (c) t=0.319 291 s 列车正常行驶时, 制动板处于水平锁闭状态, 受力分布因流场变化而不断改变, 但受力水平较小(0~10 N), 可近似看作均匀分布, 见图11.t=0.12 s时, 制动板主动开启较小角度导致流场突变, 制动板受力波动较大, 局部受力最大突变至60 N, 受力分布整体呈梯度变化, 见图12, 易产生弯曲变形. t=0.119 238 s图11 水平锁闭状态下受力分布Fig. 11 Force distribution in locking status t=0.119 639 s图12 开启瞬时受力分布Fig. 12 Force distribution at the start time of rotation 开启过程中, 制动板受力逐渐增大, 但整体处于较低水平(0~20 N). 0~2°: 受力水平为0~10 N, 可忽略受力分布变化, 看作均匀分布, 见图13; 2°~50°: 制动板顶端由于直角边缘对气流的阻滞作用, 其受力增大较快, 保持在 20 N 左右, 制动板其他部分受力较小但逐渐增大, 受力分布较均匀, 见图14; 50°~85°: 制动板顶端受力降低, 与其他部分保持同一受力水平, 制动板整体受力分布较均匀, 见图15. 图13 0~2°时受力分布Fig. 13 Force distribution from 0 to 2° 图14 2°~50°时受力分布Fig. 14 Force distributions from 2° to 50° 图15 50°~85°时受力分布Fig. 15 Force distribution from 50° to 85° 由图16可知, 制动板在t≈0.145 s时运动至垂直车顶位置, 受刚性绳约束, 运动骤停, 受力状态突变, 制动板整体受力水平增大至 100 N左右. 图17为风阻制动板稳定开启状态下的受力分布, 受力水平降低至20 N左右, 且始终保持较均匀状态. 边缘为直角的矩形制动板对气流有阻滞作用, 因而其左上角和右下角处受力始终较其他部位大, 使得制动板具有更好的增阻效果. 图16 转动骤停瞬时受力分布Fig. 16 Force distribution at the sudden stop moment of rotation 图17 稳定开启状态下受力分布Fig. 17 Force distribution in the stable opening status 制动板开启角度的变化使得阻力系数Cd和投影面积A发生变化, 制动力Fx也随之变化, 图18给出了列车车速为300 km/h时Fx与最大开启角度α的关系. 该规律与图19中高見創等[9]通过大型风洞实验所得气动阻力随风阻制动板开启角度变化的规律大体一致: 风阻制动板最大阻力不是出现在垂直开启时, 而是在开启角度为75°~85°时, 因此开启角度宜设计为75°~85°. 图18 制动力变化规律Fig. 18 Variation of braking force 图19 阻力板动作特性—打开角度特性[9]Fig. 19 Performance characteristic—opening angle[9] 图18中, 0<α<50°时,Fx随开启角度增大而增大, 且增长率逐渐增大; 50°<α<80°时,Fx继续增大, 但增长率逐渐减小; 80°<α<90°时, 增长率为负,Fx逐渐减小. 75°<α<85°时,Fx变化很小, 增长率几乎为0, 因此风阻制动板最大制动力出现在75°<α<85°时, 并非垂直开启时. 为保证可靠地获得最大制动力, 根据数据回归分析可知,Fx极大值出现在α≈80°时, 因此建议选取80°为风阻制动板的最大开启角度. 采用SPH方法建立风阻制动板流固耦合动态数值模型, 对其动态开启过程进行数值模拟, 得到如下结论: (1)当车速为300 km/h, 最大开启角度为90°时, 风阻制动板动作时间约为0.025 s, 满足紧急制动时的快速开启要求[9]. 制动板开启过程中, 速度和受力存在突变现象, 会对制动板装置造成较大冲击. 制动板稳定开启后, 角速度、 气动阻力和升力均维持在较高频率和较高振幅的稳定波动状态, 对装置的机械结构和材料性能等有较高要求. (2)锁闭状态时, 风阻制动装置对列车运行状态和周围流场几乎无影响, 制动板所受升力在0附近波动. 为保证制动板顺利开启, 制动板须主动开启一定角度(打开角度5°以下[9]). 开启初期, 板的受力有较大突变且呈梯度分布, 易产生弯曲变形; 转动过程中, 受力较小且均匀分布; 垂直开启状态下, 受力较大且分布较均匀. 制动板直角边缘处由于对气流的阻滞作用, 其受力始终较其他部位大, 制动板因而具有更好的增阻效果. (3)制动力Fx与最大开启角度α呈非线性关系, 通过数据回归分析可知, 最大制动力出现在75°<α<85°时, 而非垂直开启时[9].Fx在α≈80°时取得极大值, 建议选取80°为风阻制动板的最大开启角度. 以上结论的得出, 验证了风阻制动板应用的可行性, 通过分析运动规律、 受力分布和制动力变化规律为研制风阻制动板装置提供了可靠的理论依据.2.4 风阻制动装置箱体结构
2.5 边界条件及计算域
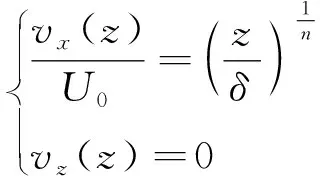
3 计算结果分析
3.1 运动规律
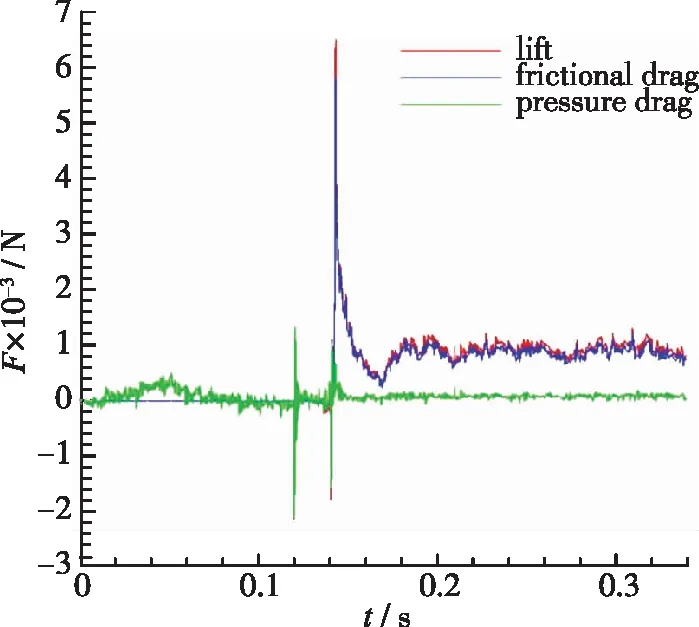

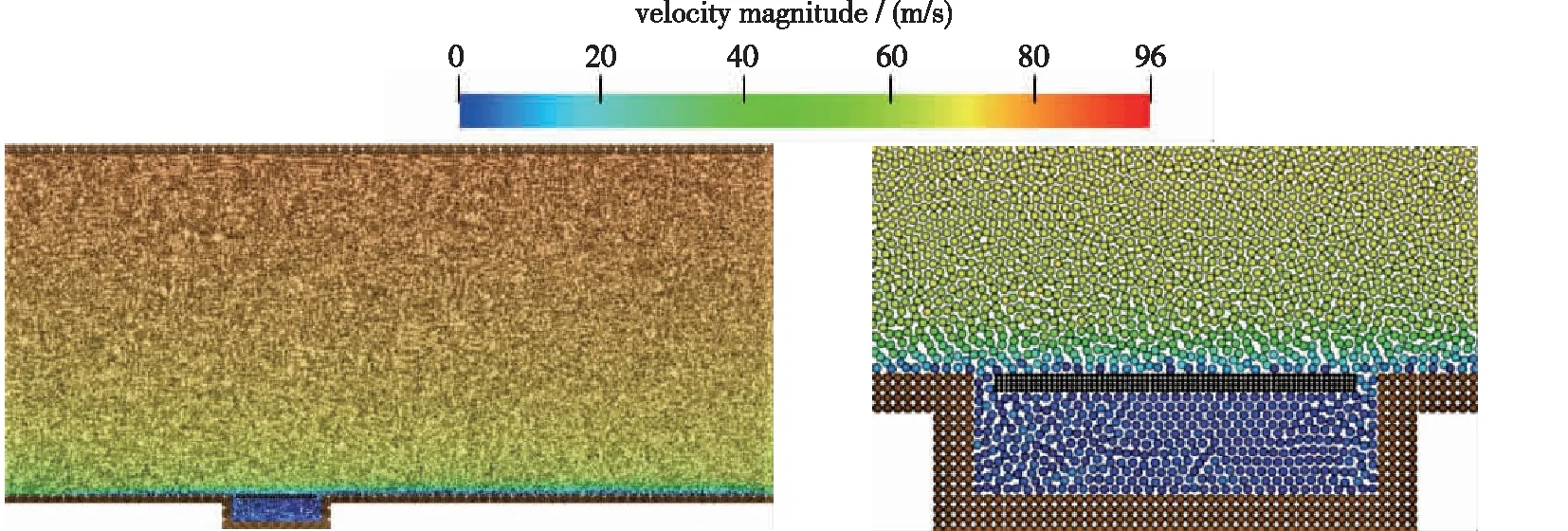






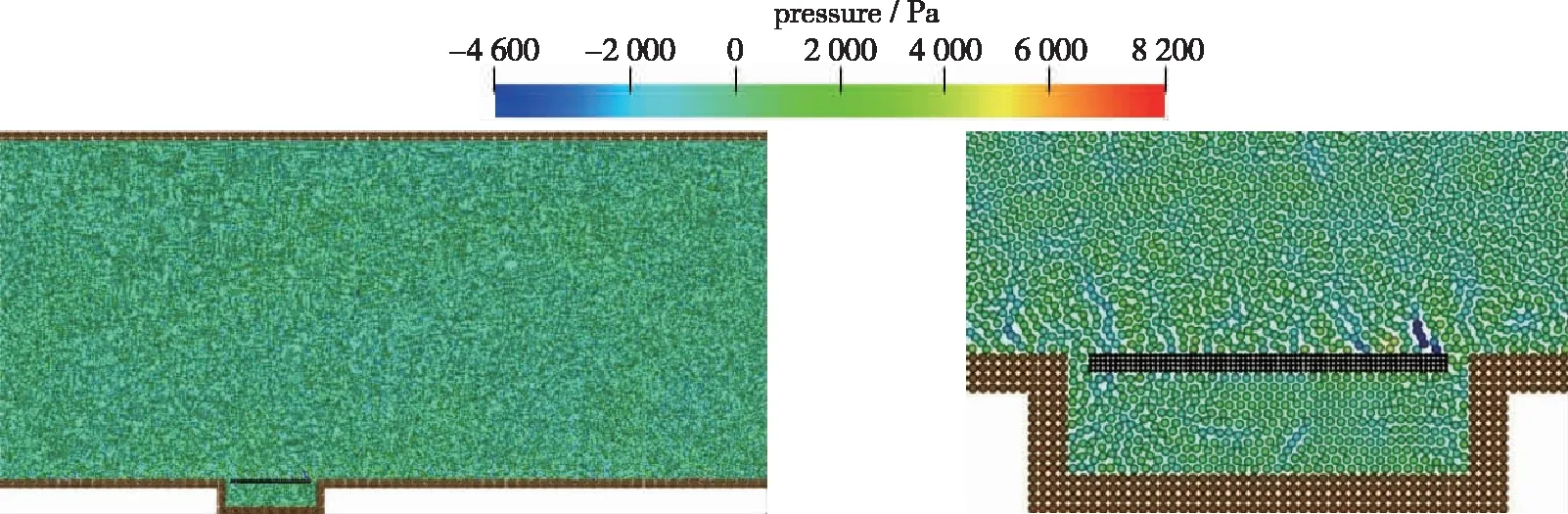






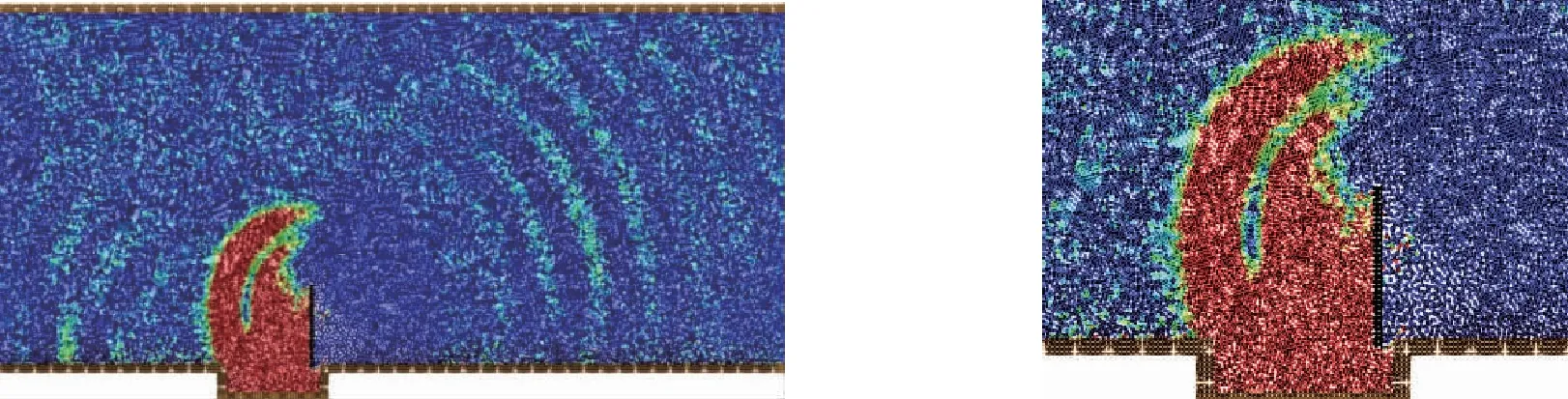



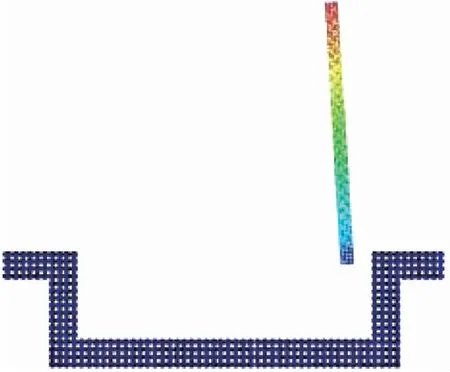
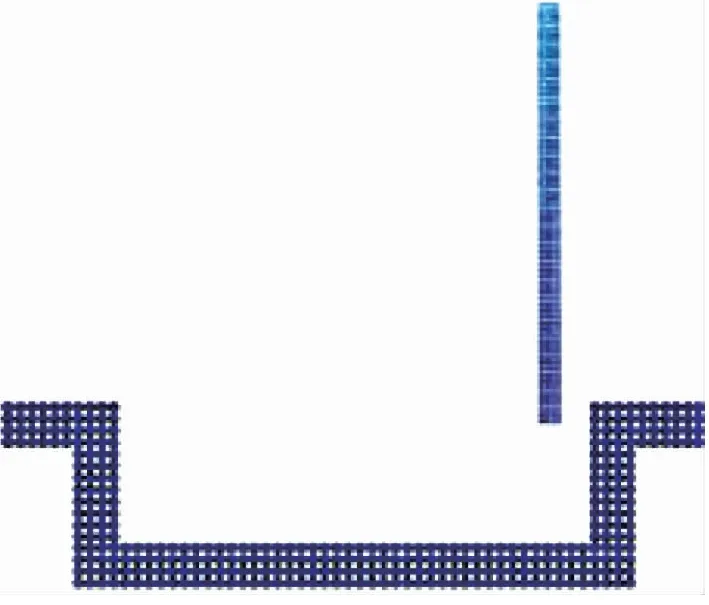



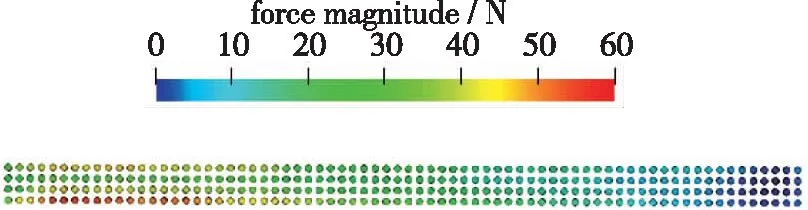
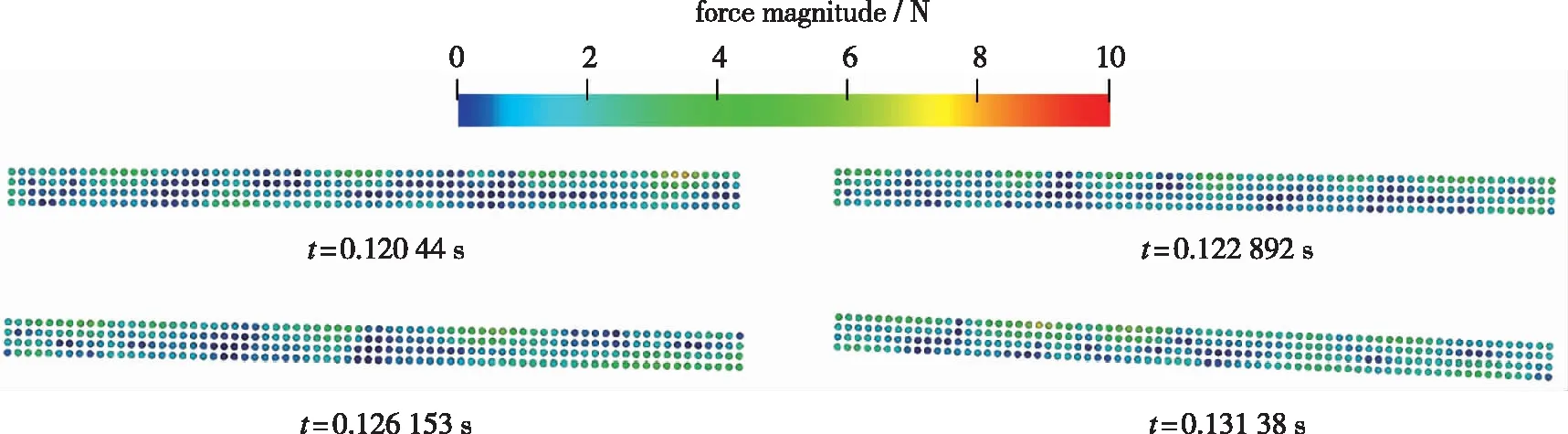
3.2 受力分布



3.3 制动力变化规律

4 结论
