立足意义建构 理解概念本质
——《百分数的意义》教学
2021-12-13刘贤虎特级教师
文|刘贤虎(特级教师)
【教学内容】
人教版六年级上册第82、83 页。
【教学过程】
一、开门见山,引发问题
师:同学们,今天这节课我们一起来学习百分数的意义。课前老师布置给大家一个小调查,让大家收集生活中百分数应用的例子,谁来分享一下?
生:某品牌酒的酒精度是42%;某品牌牛奶的浓度是100%;衣服中棉的成分占98.7%;饮料的含糖率是3.4%。
师:老师也收集了几个百分数,你能看懂这三幅图吗?

六(1)班男生有20 人,女生是男生的80%。
师:生活中百分数多吗?这说明百分数在我们生活当中的应用非常广泛。像同学们收集到的42%、100%、98.7%、3.4%,还有老师搜集的26%、60%、80%等等,这样的数都叫百分数。你知道这个符号是什么符号吗?
生:它叫百分号。
师:大家会读这些百分数吗?一起读一读。百分数和分母是100的分数的读法有什么区别?
生:百分数读作百分之几,分母是100 的分数读作一百分之几。
师:观察一下百分号是怎么写的?你觉得应该注意什么?
生:我觉得应该注意百分号的两个小圆圈不能写得太大,也不能写得太靠近中间。
师:百分数的读法和写法大家都知道了。你还想研究百分数的哪些知识?
生:我想问什么是百分数?
生:为什么我们学了分数还要学百分数?
生:百分数和之前学习的知识有关系吗?
师:这些都是好问题。我们就带着这些问题一起来进入百分数的探究之旅。
二、问题引领,理解概念
师:按照大家的想法,我们一起来研究下面三个问题。第一个问题,百分数表示什么?第二个问题,已经有了分数,我们为什么还要学习百分数?第三个问题,百分数带单位名称吗?为什么?
1.结合实例,感受意义。
出示信息:2020年东莞市卫健局调查显示,全市接近26%的小学生近视。
师:我们先研究第一个问题。请大家试着在《学习单》上表示出26%。
师:你能说说在这里26%表示什么意思吗?
生:把全市小学生的总人数看作100 格,那么近视的人数占这样的26 格。
生:如果全市小学生的总人数是100 人,那么近视的人数就是26 人。
生:假如有100 个学生,那么有26 个学生患近视。
师:假如有200 个学生,那么大约有几个学生患近视呢?如果有1000 个学生呢?
生:如果有200 个学生,大约有52 个学生近视;如果有1000个学生,大约有260 个学生近视。
师:这里的26%是表示患近视的人数吗?你们发现了什么?
生:26%表示近视的人数与总人数之间的关系。总人数在增多,近视的人数也在增多。
师:你的发现很重要,26%就是近视人数与总人数比较的结果,表示近视人数与总人数的关系。
师:你现在能不能说说百分数表示什么?
生:百分数表示两个数量比较的结果。
生:我认为百分数表示两个数之间的关系,它是把一个数平均分成100 份,取其中的几份。
生:百分数表示一个数是另一个数的百分之几。
(教师板书:百分数表示一个数是另一个数的百分之几)
2.对比数据,体会作用。
师:我们来看第二个问题,说说你是怎样想的?
哪一杯糖水更甜一些?
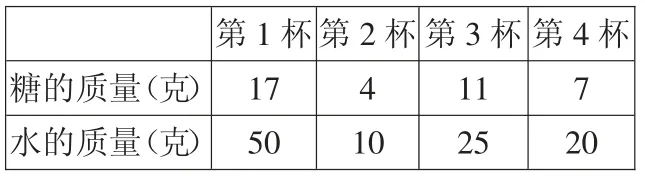
第1 杯第2 杯第3 杯第4 杯糖的质量(克) 174117水的质量(克) 50102520
(学生先独立解答,然后同桌交流,接着进行汇报)
生1:我先计算每一杯糖的质量占水的质量的几分之几,然后把它们这几个分数转化成百分数,再作比较,最后发现第3 杯是最甜的。
生2:我同意他的做法。我是把计算的结果通分,将分数化成分母为100 的分数,用它们的分子去作比较。
生3:我要补充。把它们化成百分数之后,我们就可以直接比较分子,就不用管分母了。
生4:我要补充。如果你把它们都化成分数,也可以比较大小,但是感觉用分数比较不简便。
生5:我同意他们的说法,我想补充一下为什么人们都喜欢用百分数,因为百分数不需要通分,像生2 说的如果化成分数还要通分,而百分数不用通分,所以更简便,可以节约时间。
师:同学们刚刚发现,用百分数比较大小,只看分子就可以了,感觉比较简便。当然,我们把它们化成分数、小数也可以比较,有时会麻烦一点。既然百分数能解决的问题分数和小数也能解决,那百分数到底有什么独特的作用呢?我们一起来看材料。
(课件呈现教材“你知道吗?”阅读资料。19世纪中期,德国统计学家、经济学家恩格尔对比利时不同收入的家庭消费情况进行了调查,提出了恩格尔定律……改革开放以来,我国城镇和农村居民家庭的恩格尔系数已由1978年的57.5%和67.7%分别下降到2010年的35.7%和41.1%,2019年全国居民恩格尔系数为28.2%)
师:2010年我国城镇家庭属于哪个层次?2019年全国居民家庭属于哪个层次?你是怎么看出来的?
小结:百分数确实很方便,所以在生活中经常用于分析和统计。像这样有百分数的信息在新闻报道、统计部门网站随处可见,有兴趣的同学课后可以自己去查找。
3.沟通联系,辨析区别。
师:我们来看第三个问题,你见过百分数带单位吗?为什么不带单位?
出示阅读材料:据天气预报报道,今天75%的可能会下雨,广场上有2 吨小麦需要运进仓库。一辆车每次可运吨,每次只能运走这些小麦的10%。为了提高效率,又找来三台同样的车来帮忙,这样一趟就可以运走吨,运走40%的小麦。
生:我认为百分数不带单位的原因是百分数不能表示一个非常具体的数,它表示的是一种比较的关系,比方说这个数是1000也好,2000 也好,但是它最终只是分成100 份。
师:谁听懂他的意思了?
生:我想简化他的说法,百分数表示一个数是另外一个数的百分之几,不表示一个具体的数量,所以不能带单位。
生:我补充,百分数表示的是一个分率,不是具体的量。
生:百分数表示一个数占另一个数的百分之几。运走这些小麦的10%,这个10%是运走的质量占总质量的10%,表示运走的和全部小麦的一种关系,所以它不带单位。
小结:通过对这三个问题的探究,我们对百分数有了新的认识。我们知道了百分数表示一个数是另一个数的百分之几,它是两个量比较的结果。我们还知道了百分数方便比较,在统计中有着特别重要的作用。百分数没有单位名称,因为它表示两个数量之间的关系。
三、解决问题,拓展外延
师:现在我们用百分数的知识来解决问题。请拿出《学习单》。我们来看这几道题,先独立思考,如果有问题可以同桌交流。
1.填一填:下面的正方形表示“1”,用百分数表示涂色部分。
(1)
百分数( ),
读作:( ),
表示( )是( )的( )%;
(2)
百分数( ),
读作:( ),
表示( )是( )的( )%。
2.辨一辨:哪几个分数可以用百分数来表示,哪几个不能?
师:还有补充吗?
生:我认为这里不带单位的分数一般都可以换作百分数。
生:同意,我还有补充。百分数的意义就是一个数占另一个数的百分之几。在第一题中,是指截走了的长度占了整根绳子的20%,所以可以换成百分数。第二题中,表示吨相当于吨的50%,所以它也可以化成百分数。分数可以表示具体的数量,也可以表示两个数之间的关系。而百分数只能表示两个数之间的关系。
师:大家有没有发现这一点?刚才这位同学说得非常好,他告诉我们不能化成百分数的那些分数,是因为它表示的是一个具体的数量,而能写成百分数的两个分数表示的是两个数量之间的关系。
3.比一比:课前三幅图中百分数的意义有什么不一样?
师:第二幅图中手机的电量充了60%,还差多少就可以充满?
生:还要充40%。
师:我现在再充电半小时,你估计手机电池能充到多少?
生:我估计能充到75%。
师:我再充半小时。
生:我觉得可以充到90%。
师:接着充半小时。
生:我觉得可以充到100%。
师:继续充。
生:我觉得还是100%,因为它已经充满了,就不能再增加了。
师:再充两个小时的话,它依然是——100%,它有没有可能超过100%?
生:不可能。
师:第一幅图中如果小学生没有保护好眼睛,患近视的人数有没有可能增加一些?你觉得可能达到百分之多少?
生:我认为可能达到50%。
师:最多是百分之几?这时是什么情况?
生:最多100%,表示所有的小学生都近视了。
师:当然这是我们要努力避免的极端情况,每个人都要努力保护好自己的眼睛,多运动、多做眼保健操,做好用眼卫生,让每一位同学的视力都棒棒的,争取患近视的同学只占——
生:10%。
生:0%。
师:0%是什么意思?
生:一个都没有,也就是没有同学近视。
师:一起来看第三幅图,现在男生有20 人,女生比男生多还是少?如果女生和男生人数一样多,那女生就是男生的百分之几?
生:女生比男生少。如果女生也是20 人,那么女生就是男生的100%。
师:女生有可能超过100%吗?
生:有可能。如果女生是24人,那女生就是男生的120%。
生:如果女生是40 人,那女生就是男生的200%。
师:再看看这三个信息,你有新的问题吗?
生:为什么前两个百分数都不能超过100%,而这个可以超过100%?
师:好问题。同样表示两个数之间的关系,前两个百分数都不能超过100%,而这个却可以超过100%,谁能解释这个问题?
生:因为第一和第二幅图有上限,而第三幅图是没有上限的。
生:前面两个百分数表示两个数之间的关系与后面的百分数表示两个数之间的关系是不同的,后面是两个独立的量的关系,所以可以超过100%。前两幅图是有一个上限,所以不可以超过100%。
生:我明白了。前两幅图表示的是部分与整体的关系,后面一幅图表述的是两个独立的数量,而不是部分和整体的关系。
师:这位同学说得很有道理。前两幅图表示的和后一幅图表示的关系是不一样的,你能举出这样的例子吗?
生:我想举的是和前两幅图相同的情况。比如电梯最多只能装15 人,它不能再继续装载。
生:我想举第二种情况。比如我吃了10 颗荔枝,有的同学如果吃得比我更多,就超过100%。
师:同学们,通过刚才我们对三幅图的理解和举例,进一步理解了百分数的意义,它不仅可以表示整体和部分的关系,还可以表示两个独立量的关系。其实表示两个数之间的倍数关系,我们在很早的时候就学过了。
播放微课《两个数之间的倍比关系》:我们在三年级上册学习了用整数来表示两个数之间的倍数关系,如红萝卜的根数是胡萝卜的3 倍;五年级上册学习了用小数来表示两个数之间的倍数关系,如鸵鸟的最高速度是非洲野狗的1.3 倍,用来表示倍数关系的小数可以比1 大,也可以比1 小;五年级下册时,我们还可以用分数表示两个数之间的倍数关系,如鹅的只数是鸭的;六年级上册我们认识了比,比也可以表示两个数之间的倍比关系,如宽比长等于10∶15;刚刚学的百分数表示一个数是另一个数的百分之几,即表示两个数之间的相比关系,可见倍、比、百分数都可以表示两个数之间的倍数关系。
师:通过微课我们知道了百分数表示两个数之间的倍比关系,我们之前可以用整数、小数、分数、比来表示,现在我们学的百分数也表示两个数之间的倍比关系,所以百分数也叫百分比或者是百分率。
四、全课总结,巩固概念
师:通过这节课的学习,你有什么收获?
生:我的收获是百分数代表一个数是另一个数的百分之几,不可以表示一个准确的数,它表示的是一个量与另一个量之间的关系。
生:我了解到在统计中经常会用到百分数进行比较,所以比在生活中应用非常广泛。
生:这节课我了解到了百分数后面是不能加单位的,如果是一个分数,后面有单位,不能转化成百分数。
师:看来大家通过这节课的学习都收获满满。能不能用百分数来表示你这节课的表现呢?
生:这节课我认真听讲,积极思考,积极回答问题,对自己的表现100%满意。
生:我认为自己可以表现更好,90%满意,10%不满意。
生:我不敢提出自己的问题,这一点我不满意。我积极思考,这一点很满意,85%满意。下一节课,争取100%满意。
