怎样理解平行线概念中的前提条件“在同一平面内”
2021-12-13陈佳娣
文|陈佳娣
活动一:寻找“显性平面”上的平行线。
1.请你在方格本上找到两条平行线,并画出来。
2.请你在空白纸上用三角板或直尺画一组平行线。
3.教师出示一个正方体,如图1,每条棱都标有字母。
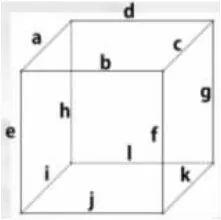
图1
(1)a 和b 是平行线吗?为什么?
(2)请你找一找图中的平行线。
学生独立完成后,交流:你找到了哪些平行线?说一说,你是怎样找的?
总结:正方体12 条棱中,两条棱之间,有的相交、有的平行。两条不相交的直线叫做平行线。
活动二:拓展理解“同一平面内”。
教师出示一组棱,如a 和f,如图2,思考:

图2
1.这两条棱的位置有什么关系?是否相交?是平行线吗?为什么?学生独立思考后,小组交流、汇报。分别请认为不是平行线和认为是平行线的学生说说,你的理由是什么?
2.深入辨析。
(1)观察开始时画的平行线,再看看棱a 和棱f,你发现有什么不一样?
(2)棱a 和棱f 分别在什么面上?引导学生发现,棱a 在左面和上面,而棱f在前面和右边,两条棱虽然没有相交,但是在不同平面内,所以两条直线不是平行线。教师点明:像这样的一组线,今后会学习到,它们属于异面直线。
推断出判断两条直线是平行线,需要一个前提条件——在同一平面内。
3.完善概念建构。
那怎样的两条直线是平行线?总结:在同一平面内的两条不相交的直线叫做平行线。如果两条直线不相交,而且“在同一平面”,那么它们是平行线;如果它们分别在两个平面上,那么它们不是平行线。
活动三:理解“隐性平面”上的平行线。
1.教师出示一组棱a 和k,如图3。思考:这两条棱也在不同的平面内,看来也不是平行线了,你们同意吗?

图3
2.学生思考、交流后,教师引导学生想象,棱a 和棱k 是否在同一个平面上?
3.教师借助实物正方体,把这个斜面切开或借助多媒体动态展示切开的过程,并摸一摸,感受这一个“隐藏”的面(图略)。
4.分类整理。请你写出该正方体的所有平行线。你还能找到一组这样的异面直线吗?
以上教学,学生经历了在方格纸上找画平行线、在空白纸上画平行线、在正方体上找平行线,通过多次辨析活动,更好地理解概念本质,积累数学活动经验、发展数学推理能力。
